南京航空航天大学 结构力学 课后习题答案 第2章
结构力学课后习题答案(2)
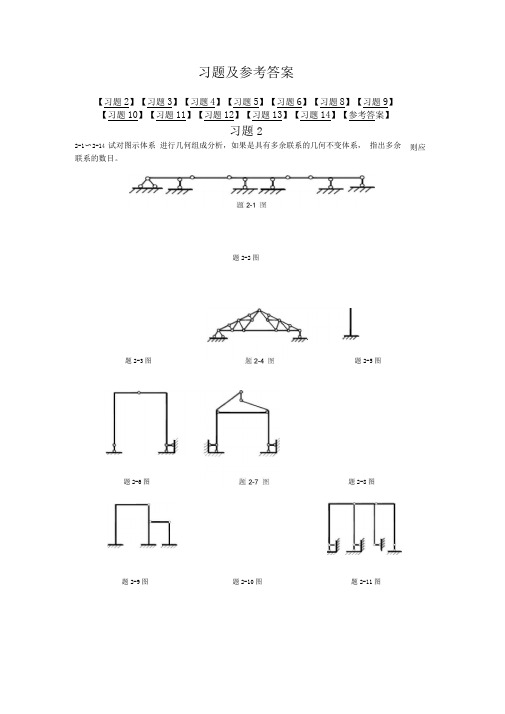
习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1〜2-14 试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,指出多余则应联系的数目。
题2-2图题2-3图题2-5图题2-6图题2-8图题2-9图题2-10图题2-11图题4-1图4-2 作图示刚架的M 图。
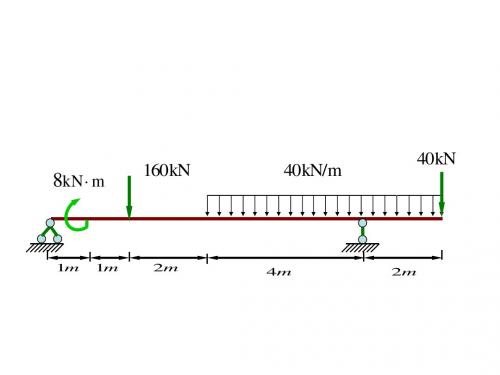
3-1 试作图示多跨静定梁的M 及Q 图。
习题(a)1.5m 1 2m I2.5m | 1.5m l 4.5m题3-1(b)3-2 试不计算反力而绘出梁的M 图。
4m40kN(a) 5kN/mM(b )4-1 作图示刚架的M 、Q 、N 图。
2kN /m2kN • m (a)2kN 题3-2习题4(b ) (c )4-3 4-4 4-54m(a)(d)作图示三铰刚架的M图。
M=4Pa2a(b)4kN4m 4m(c)珂10kN/m4m(e)题4-2图CE0.5m ]m2J 0.5m7mB7m(a)题4-3作图示刚架的M图。
(a)I 盒lUlUUW已知结构的M图,试绘出荷载。
10kN/m1.5m题4-4图urm*~ G3mC7.35m 7.35m(b)m6Nn m220kN40kN/m4m(b)C_PaPaPaa4-6 检查下列刚架的M图,并予以改正。
5-15-2 题4-5图(b)P(d)(e) (f)(c)题4-6图习题5图示抛物线三铰拱轴线方程4 f1kN/mx)x,(h)试求D截面的内力。
20kN10m题5-1图K15m j 5ml=30m带拉杆拱,拱轴线方程 y ,求截面的弯矩。
题5-3图习题66-1 判定图示桁架中的零杆。
6-2 6-3 6-4 6-5 用结点法计算图示桁架中各杆内力。
(b) (c)m题6-2用截面法计算图示桁架中指定各杆的内力。
3m [ 3m3m I 3m题6-3试求图示组合结构中各链杆的轴力并作受弯杆件的用适宜方法求桁架中指定杆内力。
结构力学习题解答(第二章)
W 3 5 (2 7 6) 5
分析:刚片ACD与刚片DEG都固接在地基上,组成一个几 何不变体系且无多余约束,而铰D、链杆BD、BF、DF均是 整个体系的内部联系,并非刚片ACD、刚片DEG与地基构 成几何不变体系的必要约束,对整个体系而言是多余约束, (一个铰相当于2个约束)。 结论:有5个多余约束的几何不变体系,
W 2 8 ( 3) 0 - 13
分析:由于该体系与地基是由三根既不相互平行也不相交于 一点的链杆连接,分析时可先抛开地基。ABF可视为一刚片, 在其基础上依次增加二元体BCF、CGA后形成扩大刚片Ⅰ; DEH可视为一刚片,在其基础上增加二元体DCH后形成扩 大刚片Ⅱ,扩大刚片Ⅰ、Ⅱ由铰C和链杆GE连接,满足两刚 片规则。 结论:无多余约束的几何不变体系
分析:刚片AB、AC与地基由铰A、B、C连接,满足 三钢片规则,形成一个几何不变体系,故链杆DE为多 余约束。 结论:有一个多余约束的几何不变体系
H G F E B A C D M N
W 2 15 (27 3) 0
分析:ABC可视为一刚片,在其基础上依次增加二元体 BFC、FDC、FED、FGE、GHE后形成扩大刚片Ⅰ,同理 HMN可视为刚片Ⅱ,刚片Ⅰ、Ⅱ由铰H和链杆DM连接,由 两刚片规则可知AHN为几何不变体系,视AHN为一大刚片, 它与地基由两刚片规则连接而成。 结论:无多余约束的几何不变体系
W 3 8 (2 10 4) 0
N
W 2 6 (8 4) 0
分析:把地基及其上的固定铰 支座链杆视为刚片Ⅰ,链杆DE 视为刚片Ⅱ,铰接三角形BCE 视为刚片Ⅲ,ⅠⅡ通过链杆1、 AD连接,形成虚铰M,ⅠⅢ通过 链杆2、AB连接,形成虚铰 C,ⅡⅢ通过链杆DB、FE连接, 形成虚铰N,铰C、M、N不共线, 满足三钢片规则。
飞行器结构力学课后答案

F2 1 P 3
3-3 平面刚架的形状、尺寸及受载情况如图所示,求刚架的弯矩和图(d)的扭矩,并作出弯 矩(扭矩)图。
8
l
1 2
4 P
3
(a) (a)解:该结构为无多余约束的几何不变结构。
Px1 0 x1 l M Pl 0 x 2 l P(l x )0 x l 3 3
1
2 4 6 7 5
3 8
(f) (f)解:分别视阴影区为三个刚片。由二刚片规则,铰 2、铰 4、铰 5 与右侧刚片组成一刚片, 再由二刚片规则该刚片与左侧刚片组成一刚片, 可知为无多余约束的几何不变系, 再与下侧 刚片组成刚片,可知该系统为无多余约束的几何不变系。
1
3
2 4
(g) (g)解:该结构为 1 次封闭刚架,外部有一多余约束。 f=3+1=4 该结构为有 4 个多余约束的几何不变系统。
N 24 2Q
N 21 N 24 2
杆件 内力 1-2
N 21 Q
2-3 0 2-4 3-4 0
Q
2Q
3
a
45°
45°
4
Q
2 1
(f)
6
(f)解: (1) f 5 3 4 2 0 故该结构为无多余约束的几何不变结构。 (2)零力杆:杆 2-3,杆 3-4,杆 1-2。
N13 3P
3
N12 3
2
N13 0
对于结点 3:
N3-4
N3-1
N 34 N 31 3P
4
对于结点 4:
N4-6
N4-3
N 46 N 43 3P
2
对于结点 2:
结构力学及习题解答

结构力学和习题解答
20
第三章 静定结构的受力分析
3.1 梁的内力 P.107 3-1 (b) (c) (e) P.108 3-2
结构力学和习题解答
21
P.107 3-1 (b) 用分段叠加法作梁的M 图
ql2
8
q
A l
ql2 8
B
ql2 8
ql2
8
ql2
8
结构力学和习题解答
22
P.107 3-1 (c) 用分段叠加法作梁的M 图
M图 FQ图
结构力学和习题解答
29
P.108 3-2 判断内力图正确与否,将错误改正 (c)
M图 FQ图
结构力学和习题解答
30
P.108 3-2 判断内力图正确与否,将错误改正 (c)
M图 FQ图
结构力学和习题解答
31
P.108 3-2 判断内力图正确与否,将错误改正 (d)
MM图图
FFQQ图图
66
((44))
22
66
((33)) 11..55 11..55
AA
BB
22
M 图(kN.m)
结构力学和习题解答
24
P.108 3-2 判断内力图正确与否,将错误改正
(a)
MM
BB
MM MM图图
FFQQ图图
结构力学和习题解答
25
P.108 3-2 判断内力图正确与否,将错误改正
(a)
MM
BB
MM MM图图
FFQ图Q图
结构力学和习题解答
26
P.108 3-2 判断内力图正确与否,将错误改正 (b)
MM图图
南京航空航天大学 飞行器结构力学 课后习题答案 第1章

第一章 弹性力学基础1-1 上端悬挂、下端自由的等厚度薄板,其厚度为1,容重为ρ。
试求在自重作用下的位移分量表达式。
解:如图1-1建立坐标系.利用x σ沿y 方向均匀分布及x 方向的力平衡条件0=∑x 可得,⎪⎩⎪⎨⎧==-= x l xyy x 00)(τσρσ 又因为1()()x y u u l x x E Eρσσ∂=-=-∂ )()(1x l Eu u E y vx y --=-=∂∂ρσσ 积分得)()21(12y f x lx u +-=Eρ)()(2x f y x l uv +--=Eρ又由对称性 0)(020=⇒==x f v y 由 2110()2xy u v f y uy y x Eτρ∂∂=+=⇒=-∂∂ 综上所述有2221)21(uy Ex lx u ρρ--=Ey x l uv )(--=Eρ1-2 写出图1-2所示平面问题的应力边界条件。
解:上表面为力边界,100=,=,=,m l q lxl X --=Y 。
代入x xy xy y l m Xl m Yσττσ⎧+=⎪⎨+=⎪⎩ 中得到上表面的边界条件为00=--=xy y x q lxl τσσ;=;下表面为自由边,边界条件为000==xy y x τσσ;=;侧面为位移边界。
1-3 矩形板厚为1。
试用应力函数22A xy ϕ=求解。
(并画出面力分布图)解:应力函数22A xy ϕ=满足应力函数表示的变形协调方程,可以作为解。
在无体力的情况下,矩形板的应力为22x Ax yϕσ∂==∂220y x ϕσ∂==∂2xy Ay x yϕτ∂=-=-∂∂根据应力边界条件公式x xy xy y l m X l m Yσττσ+=+=各边的应力边界为a d 边: 0,1l m == 20A X A y h Y ⎧=-=-⎪⎨⎪=⎩ c b 边: 0,1l m ==- 20A X A y hY ⎧==-⎪⎨⎪=⎩a b 边: 1,0l m =-= 0X Y A y⎧=⎪⎨=⎪⎩c d 边: 1,0l m == X A x A lY A y⎧==⎪⎨=-⎪⎩根据以上各边的应力边界条件,可画出矩形板的面力分布图如图1-3a 。
结构力学课后习题答案

习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
(b)(a)20kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。
(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
(c)(b)(a)20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。
P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。
(b)(a)题4-3图4-4 作图示刚架的M 图。
(a)题4-4图4-5 已知结构的M 图,试绘出荷载。
(b)(a)题4-5图4-6 检查下列刚架的M 图,并予以改正。
(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l lfy )(42-=,试求D 截面的内力。
题5-1图5-2 带拉杆拱,拱轴线方程x x l lfy )(42-=,求截面K 的弯矩。
C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。
(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
(a)题6-4图6-5 用适宜方法求桁架中指定杆内力。
(c)(b)(a)题6-6图习题88-1 试作图示悬臂梁的反力V B 、M B 及内力Q C 、M C 的影响线。
结构力学课后习题答案
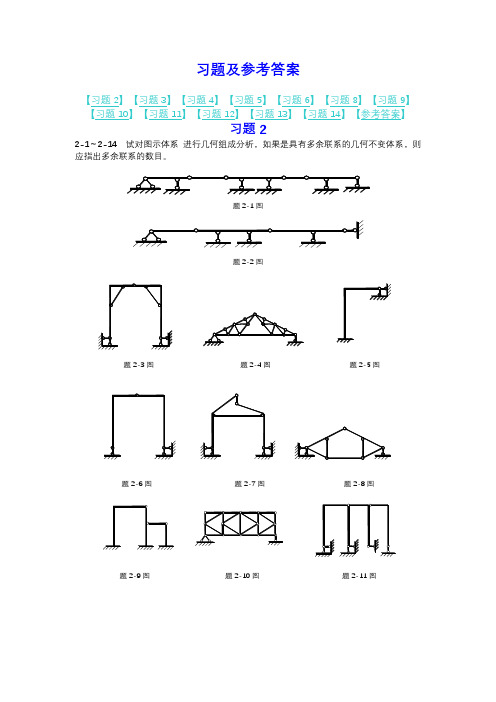
习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
题3-1图3-2 试不计算反力而绘出梁的M 图。
题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
题4-1图4-2 作图示刚架的M 图。
(b)(a)20kN40kN20kN/m40kN(b)5kN/m40kN(a)(c)(b)(a)题4-2图4-3 作图示三铰刚架的M 图。
题4-3图4-4 作图示刚架的M 图。
题4-4图4-5 已知结构的M 图,试绘出荷载。
P(e)(d)(a)(b)(c)/4kN(b)(a)(a)(b)(a)题4-5图4-6 检查下列刚架的M 图,并予以改正。
题4-6图习题55-1 图示抛物线三铰拱轴线方程,试求D 截面的内力。
题5-1图5-2 带拉杆拱,拱轴线方程,求截面K 的弯矩。
题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(e)(g)(h)P(d)(c)(a)(b)(f)x x l l fy )(42-=x x l lfy )(42-=C题6-1图6-2 用结点法计算图示桁架中各杆内力。
题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
题6-4图6-5 用适宜方法求桁架中指定杆内力。
(c)(b)(b)(b)(a)题6-6图习题88-1 试作图示悬臂梁的反力V B 、M B 及内力Q C 、M C 的影响线。
结构力学课后习题答案

习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
(b)(a)20kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。
(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
(c)(b)(a)20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。
P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。
(b)(a)题4-3图4-4 作图示刚架的M 图。
(a)题4-4图4-5 已知结构的M 图,试绘出荷载。
(b)(a)题4-5图4-6 检查下列刚架的M 图,并予以改正。
(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l lfy )(42-=,试求D 截面的内力。
题5-1图5-2 带拉杆拱,拱轴线方程x x l lfy )(42-=,求截面K 的弯矩。
C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。
(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
(a)题6-4图6-5 用适宜方法求桁架中指定杆内力。
(c)(b)(a)题6-6图习题88-1 试作图示悬臂梁的反力V B 、M B 及内力Q C 、M C 的影响线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
南京航空航天大学结构力学课后习题答案第2章第二章薄板的弯曲2-1 写出2-1图所示矩形薄板的边界条件。
OA为简支边,并作用有分布的弯矩M。
BC边为固支边,OC边为简支边。
AB边为自边。
解:OA边:wx?0?0;Mx MyOC边:wy?0?0;x?0?2w?2w?2w??D(2?u2)??D2??M?x?yx?0?xx?0?0y?0y?0?2w?2w?2w??D(2?u2)??D2?y?xy? 0?y ?wBC边:wx?a?0;?0 ?xx?aAB边:My?2w?2w??D(2?u2)?0 ?y?xy?b?M yx?x)y?by?b(Qy??3w?3w??D[3?(2?u)2]?0 ?y?x? yy?b 2-2 如图2-2所示,矩形薄板OA边和OC边为简支边,AB和BC为自边,在点B受向下的横向集中力P。
试证w?mxy可作为该薄板的解答,并确定常数m、内力及边界处反力。
解:w?mxy满足平衡微分方程?4w?q/D?0 OC边上:wy?0?2w?2w?0;?D(2?u2)=0 ?y?xy?0OA边上:wx?0?2w?2w?0;?D(2?u2)=0 ?x?yx?0?2w?2w?3w?3w?0;?D[3?(2?u)2]?0 AB边上:?D(2?u2)?y?xy?b?y?x?yy?b?2w?2w? 3w?3wBC边上:?D(2?u2)?0;?D[3?(2?u)]?0 ?x?yx?a?x?x?y2x?a?2w)??2D(1?u)m?? P 在B点上:?2D(1?u)(?x?yx?a,y?b ?m?P 2D(1?u)所以w?Pxy 2D(1?u)?2w?2w?2w?2wMx??D(2?u2)?0;My??D(2?u2)?0;?y?x?x?yMxy??? 2wPQx??D?2w?0;Qy??D?2w?0 ??D(1?u)?? ;?x?y?x? y2?2wRA??2D(1?u)()??P?RC;RO?P ?x?yA 2-3 如图2-3所示,半椭圆形薄板,直线边界为ACB 为xx2y2固支边,承受横向载荷q=q0。
试证w?mx(2?2?1)2可作为解答,求出常数aabm,最大挠度和点的弯矩。
x4y4x2y2x2y2解:w?mx(4?4?222?22?22?1)ababab?4wmx?120?x4a4?4wmx?24?y4b42?4w?x?y?48mx22a2 b2将式代入薄板的挠度方程D?4w?q 即D?4w?mD(120xa4?48xa2b2?24xb4)?q?qx0aqxm?024D(5a21a4?a2b2?b4) ?q0a 3a2a424D(5?2b2?b4)w?q0a3xx2y2(2?2?1)224D(5?2a2a4abb2?b4)求最大挠度:根据对称性可知最大挠度必在y?0上,代入下式?w5x4?x?m(y4ab?6x2y2x2y24?4 a2b2?6a2?2b2?1)?0?w32?y?mx(4yxyyb4? 4a2b2?4b4)?0则有?w?m(5x4x2?xy?0a4?6a 2?1)?0?w?yy?0?0 式可解出a22x?,x?a2 52即x?5a及x?a 5显然在x?5a处使得w取最大值为5wmax?m51(?1)2a55 25q0a4?a2a4375(5?22?4)Dbb根据公式弯矩?2w?2wMx??D(2??2) ?x?y 而?2w20x3xy2x?m(?12?12) 24222?xaaba?2w12xy24x34x?m(4?22?2) 2?ybabb ?Mx60x212y21212y212x24 ??D[4?22?2]??(4?22?2)m?0 ?xaabaaabb? Mxxyxy??D[2422?24?4]?0 ?yabb及对称性,可知在y?0,x?a(3?153?)(??)处2222abab4124??20(Mx)x????Dm?(4??22) ?3?(2??2)?? abab?a?其中??a(3?153?)(??)。
a2b2a2b2而Mx在C 点,即x?a,y?0处的值为?2012?(Mx)C??Dm????aa? ?q0a2 ?a2a43(5?22?4)bb2-4 有一矩形薄板,边长为a和b。
若其挠度函数为w=Cxy(a-x)(b-y),求该薄板受什么样的载荷和边界的支持条件。
解:?w?Cxy(a?x)(b?y)?Cabxy?Caxy2?Cb x2y?Cx2y2 ??w?Caby?Cay2?2Cbx y?2Cxy2;?x?w?Cabx?2Caxy?Cbx2?2C x2y;?y?2w?2w2??2Cby?2Cy;2??2Cax?2Cx2;2?x?y?4w?4w?4w?4C;4?0;4?0 22?x?x?x?y ?4w?q/D?2?4C?q/D?q? 8CD x?0时:wx?0?0;?w?x?0不是固支边,是简支边x?0 (Mx)x?0?2w??D2?2CD(y2?by)?Mx?xx?0?w?x?0不是固支边,是简支边x?ax?a时:wx?a?0;(Mx)x?a?2w??D2?2CDy(b?y)?Mx ? xx?a?w?y?0不是固支边,是简支边y?0y?0时:wy?0?0;(My)y?0?2w??D2?y?w?y?2CDx(a?x)?My y?0y?b时:wy?b?0;?0不是固支边,是简支边y?b (My)y?b?2w??D2?y?2CDx(a?x)?Myy?b2-5 四边简支正方形薄板,边长为a,在板中点受横向载荷P,试求最大挠度。
解:具体求解过程参照教材P52?P55。
针对边长为a的四边简支正方形薄板在板中点受横向载荷P。
最大挠度为wmax4P?42?Da?4Pa?4D2a4??222m?1n?1 (m?n)????1??222m?1n?1(m?n) 精度取决于取多小项。
当取m?n?1时,最大挠度为wmax?/D 2-6四边简支矩形薄板,边长为a和b,受横向分布载荷q?q0sin试证挠度函数w?msin 置。
解:挠度函数w?msin?xasin?yb,?xasin?yb是该板的解。
并求最大挠度、最大弯矩及其位?xasin?yb满足四边简支的边界条件。
即?2w在x?0,x?a处,w?0,2?0 ?x?2w在y?0,y?a处,w?0,2?0 ?y 于?4w?4?x?y?msinsin?x4a4ab?4w? 4?x?y?msinsin?y4b4ab?4w?4?x?y?msinsi n2222?xyabab所以?4w?( 1214?x?y??)?msinsin 4224aabbabq0?x?y?sinsinDabq0121??)?a4a2b2b4D?m?4(q0a4 ?m?4222?(1?ab)D 则挠度函数为q0a4?x?y w?4sinsin?(1?a2b2)2Dab在x?a/2,y?b/2处,挠度取得最大值wmax弯矩q0a4 ?4?(1?a2b2)2D?2w?2w?2?2?x?yMx? ?D(2??2)?Dm[2??2]sinsin?x?yababMy?? D(?w?w???x?y??)?Dm[??]sinsin2222?y?x baab2222 在x?a/2,y?b/2处,弯矩取得最大值(Mx)maxq0a2(1??a2b2)?2?(1?a2b2)2(My) maxq0a4(1??b2a2) ?22222?b(1?ab) 2-7 如图2-7,四边简支矩形薄板上作用有三角形分布载荷,即p(x,y)?q0xa 试用双重三角级数方法求挠度函数。
解:薄板弯曲的基本微分方程为D?4w?p(,xy)边界条件是在x?0和x?a处,w?0,?2w?x2?0在y?0和y?b处,w?0,?w?y?0挠度用双重三角级数表示为w???Amnsinm?1n?1??22m?xn?y sinab其中m和n是任意整数,Amn为待定系数。
显然,(3)式满足式所述的全部边界条件。
将式代入式,得?m2n2?m?xn?y4?D???2?2?Amnsinsindxdy?p(x,y)ababm?1n?1????2为了求出系数Amn,必须先将式右端的载荷展开成与左端同样的双重三角级数形式p(x,y)???Cmnsinm?1n?1??m?xn?y sinabi?x,其中i为任意正整数。
然a先求出系数Cmn。
将式的左右两端都乘以sin后对x积分,积分限从0到a,并注意a?sin0(m?i)?0m?xi?x sindx??aa?a2(m?i)得到i?xa?n?y p(x,y)sindx?Csin?in?a2n?1b0再将上式两端都乘以sin从0到b,得到baaj?y,其中j也是任意正整数。
然后对y积分,积分限b??p(x,y)sin00i?xj?yabsindxdy?Cij ab4因为i和j是任意整数,故可以改写为m 和n。
所以从上式可得Cmn4m?xn?y?p(x,y)sinsindxdyab??ab00?2ab将式代入式,得?m2n2?m?xn?y4?D???2?2?Amns insindxdyb?abm?1n?1?a ??m?xn?y???Cm nsinsinabm?1n?1?两个相同的级数要相等,必须使相应项的系数都相等,从而得ab Amn?4??p(x,y)sin00m?xn?ysindxdyab222 ?4Dab?将p(x,y)?q0xa代入上式。
?mn??2?2b??a m?xn?ym?xn?yp(x,y)sinsindxdy?qxasinsin dxdy0????abab0000?2bn?yb??sindy?[1?c osn?]??n?bn?0??0babab(n为奇数) ab??q0xasin00am?xn?ysindxdyabm?x2bd x?an?(n为奇数)??q0xasin0 (n为奇数)(n为奇数)=2bq0??acosm??mn?2(?1)m?12abq0? mn?2(?1)m?18q0将式代入式得到系数Amn??mn??22?ab??222?6 Dmn?将式代入式得到挠度函数8qw?06D?(?1)m?1m?xn?ysinsin ??22mna bm?1n?1,3,5mn(2?2)2ab??2-8 已知圆形薄板的挠度方程为w?C[(5??)a4?2(3??)a2r2?(1??)r4] 式中a是板的半径,C是常数。
试确定该挠度方程对应于怎样的边界条件和什么样的载荷?并求出板的弯矩方程式。
解:因为挠度方程只是关于r的函数,故该圆形薄板的弯曲是轴对称弯曲。
(w)r?a?C[(5??)a4?2(3??)a2a2?(1??)a]4?C[(5??)a4?(6?1??)a4]?0((1) dw)r?a?C[?4(3??)a3?4(1??)a3](2) dr??8Ca3d2w(2)r?a?C[?4(3??)a2?12(1??)a 2](3) dr?8?Ca3(Mr)r?ad2w?dw??D[2?]drrdr??D[8?Ca2?? 0?a8Ca2](4) 式、式(wr)r?a?0,(Mr)r的边界条件为简支边。
