五点法画三角函数图像
三角函数正弦余弦的图象与五点法

6
6 3 2 3 6 2
●
2 0
11
6
32
2 5 ●
36
●
●
x
●
5
6
-1
●
●
●
3
sin(2k+x)= sinx (k Z)
y y=sinx (xR)
1
2 0
-1
2 3 4 5 6 x
二、正弦函数的“五点画图法”
(0,0)、( , 1)、( ,0)、( 3 ,-1)、 (2 ,0)
2
2
y
1
●
●
0
2
-1
●
3
2
●
●
2
x
y●1源自●02-1
●
3
2
●
●
2
x
练习:用“五点画图法”画出正弦函数
y=sinx(x[0, 2]的图象
三、余弦函数y=cosx(x R)的图
象
sin( x+
)= cosx
2
y
y=sinx的图象
1
2 0 3 2 3
2 -1 2
2
4 5
y=cosx的图象
6 x
1+sinx 1 2
1
0
1
y
2
●
y=1+sinx x [0, 2 ]
1●
●
●
●
o
3
2
x
2
2
(2)按五个关键点列表
x
0
2
3 2
2
cosx 1 0 -1 0 1
-cosx -1 0
1
0 -1
五点作图法课件

C 将 新疆 王新敞
y=-sin2x
图象上的横坐标变为原来的
1
倍,纵坐标变为原来的相反数,
奎屯
2
即得到 y=sinx 的图象
D 将 新疆 王新敞
y=-3sin2x
图象上的横坐标缩小一倍,纵坐标扩大到原来的
1
倍,
奎屯
3
且变为相反数,即得到 y=sinx 的图象
•五点作图法
•7
三、练习
2 将函数 新疆 王新敞
•3
二、知识点
2、五点法的应用,根据图象求函数解析式;
由函数 y=Asin(ωx+ )+b 的图象求其解析式,一般来说,如对所求 函数式中的 A、ω、 不加限制(如 A、ω的正负,角 的范围等),那么
所求的函数式应有无数多个不同的形式(这是由于所求函数是周期函数所
致),因此这类问题多以 A>0, ω>0, | |< 形式出现,我们解这类题
y=f(x)的图象沿
x
轴向右平移
,再保持图象上的纵坐标不变,
奎屯
3
而横坐标变为原来的 2 倍,得到的曲线与 y=sinx 的图象相同,则 y=f(x)是(C )
A
新疆 王新敞
y=
sin(
2x+
)
奎屯
3
B
新疆 王新敞
y=
sin(
2x-
)
奎屯
3
2 C
新疆 王新敞
y=
sin(
2x+
)
奎屯
3
2 D
新疆 王新敞
T
ωx + :称为相位 新疆 王新敞
x=0 时的相位 称为初相
奎屯
•五点作图法
5.4.1 正弦函数、余弦函数的图象(解析版)

5.4.1 正弦函数、余弦函数的图象一、正弦函数、余弦函数图象的画法1.描点法:按照列表、描点、连线三步法作出正弦函数、余弦函数图象的方法. 2.几何法:利用三角函数线作出正弦函数和余弦函数在]2,0[π内的图象,再通过平移得到x y sin =和cos y x =的图象.3.五点法:先描出正弦曲线和余弦曲线的波峰、波谷和三个平衡位置这五个点,再利用光滑曲线把这五点连接起来,就得到正弦曲线和余弦曲线在一个周期内的图象.在确定正弦函数x y sin =在]2,0[π上的图象时,关键的五点是:)0,2(),1,23(),0,(),1,2(),0,0(ππππ-【注意】(1)若x R ∈,可先作出正弦函数、余弦函数在]2,0[π上的图象,然后通过左、右平移可得到x y sin =和cos y x =的图象.(2)由诱导公式cos sin()2y x x π==+,故cos y x =的图象也可以将x y sin =的图象上所有点向左平移2π个单位长度得到. 二、正(余)弦函数的图象 函数y =sin xy =cos x图象图象画法五点法五点法关键五点 (0,0),π(,1)2,(,0)π,3π(,1)2-,(2,0)π (0,1),π(,0)2,(,1)π-,3π(,0)2,(2,1)π正(余)弦曲线正(余)弦函数的图象叫做正(余)弦曲线三、用三角函数图象解三角不等式的方法1、作出相应正弦函数或余弦函数在[0,2π]上的图象;2、写出适合不等式在区间[0,2π]上的解集;3、根据公式一写出不等式的解集.题型一 五点法作三角函数的图象【例1】用“五点法”作y =2sin2x 的图象,首先描出的五个点的横坐标是( ) A .30,,,,222ππππ B . 30,,,,424ππππ C .0,,2,3,4ππππD .20,,,,6323ππππ【答案】B【解析】由“五点法”作图知:令2x =0,2π,π,32π,2π,解得x =0,4π,2π,34π,π,即为五个关键点的横坐标,故选:B.【变式1-1】用“五点法”作函数cos 1y x =-,[]0,2x π∈的大致图像,所取的五点是______.【答案】(0,0),,12π⎛⎫- ⎪⎝⎭,(,2)π-,3,12π⎛⎫- ⎪⎝⎭,(2,0)π【解析】由“五点法”作函数cos 1y x =-,[0x ∈,2]π的图象时的五个点分别是(0,0),,12π⎛⎫- ⎪⎝⎭,(,2)π-,3,12π⎛⎫- ⎪⎝⎭,(2,0)π.【变式1-2】用“五点法”画出下列函数的简图:(1)cos 1y x =-,[],x ππ∈-; (2)sin y x =,3,22x ππ⎡⎤∈-⎢⎥⎣⎦; (3)sin y x =-,[]0,2x π∈.【答案】(1)见解析;(2)见解析;(3)见解析 【解析】(1)按五个关键点列表xπ-2π-2ππcos x1-0 11cos 1x -2- 1- 01- 2-(2)按五个关键点列表x2π-0 2ππ32πsin x1- 011-描点并将它们用光滑的曲线连接起来如下图(3)按五个关键点列表x0 2ππ32π2πsin x11-sin x -0 1-0 1 0【变式1-3】用“五点法”作下列函数的简图. (1)2sin ([0,2])y x x π=∈;(2)5sin()([,])222y x x πππ=-∈. (3)2sin(2)3y x π=-(x ∈R ).【答案】(1)图象答案见解析;(2)图象答案见解析;(3)图象答案见解析. 【解析】(1)列表如下:x2ππ 32π2π 2sin x 02 0 -2 0描点连线如图:(2)列表如下:x2ππ 32π2π 52πsin()2x π-0 1 0 -1 0(3)函数π2sin 23y x ⎛⎫=- ⎪⎝⎭在长为一个周期π的区间上的图象,列表如下:x6π512π23π1112π76π23x π-0 2ππ32π2πy 02 0 -2 0再向左右两边扩展,其图象如下:题型二 含绝对值的三角函数【例2】函数y =|cos x |的一个单调增区间是( )A .,22ππ⎡⎤-⎢⎥⎣⎦B .[0,π]C .3,2ππ⎡⎤⎢⎥⎣⎦D .3,2π2π⎡⎤⎢⎥⎣⎦【答案】D【解析】将y =cos x 的图像位于x 轴下方的图像关于x 轴对称翻折到x 轴上方,x 轴上方(或x 轴上)的图像不变,即得y =|cos x |的图像根据各选项判断只有D 选项正确. 故选:D.【变式2-1】作出函数2sin sin y x x =+,[],x ππ∈-的大致图像. 【答案】图见解析【解析】函数[][]3sin ,0,2sin sin sin ,,0x x y x x x x ππ⎧∈⎪=+=⎨-∈-⎪⎩, 其图如下所示:【变式2-2】作出函数sin ||,[2,2]=∈-y x x ππ的大致图像. 【答案】图象见解析 【解析】列表x0 2ππ32π2πsin ||y x =1 0 -1 0作图:先作出(]0,2π的图像,又原函数是偶函数,图像关于y 轴对称, 即可作出[)2,0π-的图像.【变式2-3】作函数3sin 2y x π⎛⎫=+ ⎪⎝⎭的图象.【答案】图象见解析.【解析】3sin cos 2y x x π⎛⎫=+= ⎪⎝⎭ cos 22,Z 223cos 22,Z 22x k x k k x k x k k ππππππππ⎧⎛⎫-+≤≤+∈ ⎪⎪⎪⎝⎭=⎨⎛⎫⎪-+<<+∈ ⎪⎪⎝⎭⎩故|cos |y x =的图象是cos y x =的图象在x 轴下方的部分翻折到x 轴上方后得到的图象,如图题型三 三角函数识图问题【例3】函数1sin =+y x x的大致图象是( )A .B .C .D .【答案】A【解析】函数1sin =+y x x是定义域(,0)(0,)-∞+∞上的奇函数∴其图象关于原点对称,排除选项D ;当(0,)x π∈时,sin 0x >,此时1sin 0x x+>,∴当(0,)x π∈时,()f x 的图象在x 轴上方,排除选项B ; 当32x π=时,322sin 10233πππ+=-+<,()f x 的图象在x 轴下方,排除选项C ;综上所述,函数1sin =+y x x的大致图象为选项A .故选:A .【变式3-1】函数2sin 2xy x =-的图象大致是( )A .B .C .D .【答案】A【解析】令0x =,则02sin 01y =-=,排除C 、D ;令1x =-,则()112sin 2sin 202y -=--=+>,排除B.故选:A【变式3-2】已知函数()y f x =的图象如图所示,则此函数可能是( )A .()sin ln ||f x x x =⋅B .()sin ln ||f x x x =-⋅C .()sin ln f x x x =⋅D .()|sin ln |f x x x =⋅ 【答案】A【解析】图象关于原点对称,为奇函数,CD 中定义域是0x >,不合,排除,AB 都是奇函数,当(0,1)x ∈时,A 中函数值为负,B 中函数值为正,排除B .故选:A .【变式3-3】已知函数()f x 的部分图象如图所示,则()f x 的解析式可能为( )A .()sin πf x x x =B .()(1)sin πf x x x =-C .[]()cos π(1)f x x x =+D .()(1)cos πf x x x =- 【答案】B【解析】对于A ,()()sin πsin π()f x x x x x f x -=--==,所以函数()sin πf x x x =为偶函数,故排除A ; 对于D ,()010f =-≠,故排除D ;对于C ,[]()cos π(1)cos πf x x x x x =+=-,则()()cos πf x x x f x -==-, 所以函数[]()cos π(1)f x x x =+为奇函数,故排除C.故选:B.题型四 利用图象解三角不等式【例4】不等式2sin ,(0,2)2xx π∈的解集为( ) A .,62ππ⎡⎤⎢⎥⎣⎦ B .3,44ππ⎡⎤⎢⎥⎣⎦ C .423,ππ⎡⎤⎢⎥⎣⎦ D .,64ππ⎡⎤⎢⎥⎣⎦【答案】B 【解析】2sin ,(0,2)2xx π∈ sin y x =函数图象如下所示:∴344ππ≤≤x ,∴不等式的解集为:3,44ππ⎡⎤⎢⎥⎣⎦.故选:B .【变式4-1】在()0,2x π∈上,满足cos sin x x >的x 的取值范围( )A .5,44ππ⎛⎫ ⎪⎝⎭B .0,4π⎛⎫ ⎪⎝⎭C .50,,244πππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭ D .5,24ππ⎛⎫⎪⎝⎭【答案】C【解析】作出sin y x =和cos y x =在()0,2x π∈的函数图象,根据函数图象可得满足cos sin x x >的x 的取值范围为50,,244πππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭.故选:C.【变式4-2】在[]0,2π内,不等式3sin x < ) A .(0,π) B .3,34ππ⎛⎫ ⎪⎝⎭C .45,33ππ⎛⎫ ⎪⎝⎭ D .5,23ππ⎛⎫⎪⎝⎭【答案】C【解析】画出y =sin x ,[]0,2x π∈的草图如下.[]0,2x π∈内,令3sin x =43x π=或53x π=,结合图象可知不等式3sin x <的解集为45,33ππ⎛⎫ ⎪⎝⎭.故选:C .【变式4-3】若函数()2sin13f x x π=- )A .56,622k k ππππ⎡⎤++⎢⎥⎣⎦(k ∈Z ) B .156,622k k ⎡⎤++⎢⎥⎣⎦(k ∈Z )C .56,644k k ππππ⎡⎤++⎢⎥⎣⎦(k ∈Z ) D .156,644k k ⎡⎤++⎢⎥⎣⎦(k ∈Z ) 【答案】B【解析】要使函数有意义,则2sin103x π-≥,即1sin32x π≥, 即522636k x k πππππ+≤≤+,k ∈Z ,得156622k x k +≤≤+,k ∈Z , 即函数的定义域为156,622k k ⎡⎤++⎢⎥⎣⎦(k ∈Z ).故选:B【变式4-4】已知()f x 的定义域是3⎡-⎢⎣⎦,则(sin 2)f x 的定义域为( ) A .2,36k k ππππ⎡⎤-++⎢⎥⎣⎦,k Z ∈ B .,63k k ππππ⎡⎤++⎢⎥⎣⎦,k Z ∈C .22,236k k ππππ⎡⎤-++⎢⎥⎣⎦,k Z ∈ D .2,263k k ππππ⎡⎤++⎢⎥⎣⎦,k Z ∈【答案】A 【解析】()f x 的定义域是3⎡-⎢⎣⎦,故由31sin 2x -≤≤解得()422233k x k k Z ππππ-+≤≤+∈, ()236k x k k Z ππππ∴-+≤≤+∈ 因此,函数(sin 2)f x 的定义域为()22,236k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦.故选:A.【变式4-5】函数y 12log sin x________. 【答案】{}22,x k x k k Z πππ<<+∈ 【解析】由1122log sin 0log 1x ≥=知,0sin 1x <≤,由正弦函数图象特征知,22,k x k k Z πππ<<+∈. 故定义域为{}22,x k x k k Z πππ<<+∈. 故答案为:{}22,x k x k k Z πππ<<+∈.题型五 与正余弦函数有关的零点【例5】函数sin y x =,[]0,2πx ∈的图像与直线23y =-的交点的个数为( ) A .0 B .1 C .2 D .3 【答案】C【解析】在同一平面直角坐标系内,先画函数sin y x =,[]0,2πx ∈的图像,再画直线23y =-,可知所求交点的个数为2.故选:C .【变式5-1】已知函数f (x )=12x⎛⎫⎪⎝⎭-sin x ,则f (x )在区间[0,2π]上的零点个数为( )A .1B .2C .3D .4 【答案】B【解析】令sin 01()2xf x x ⎛⎫-=⎪⎝⎭= ,则1()sin 2x x =, 在同一坐标系中,作出1(),sin 2xy y x ==,如下图所示:由图知,f (x )在区间[0,2π]上的零点个数为2个.故选:B.【变式5-2】()f x 是定义在R 上的偶函数,且()()11f x f x -=+,[]1,0x ∈-时,()sin 2f x x ππ⎛⎫=+⎪⎝⎭,则函数()()e x g x f x -=-在区间[]2021,2022-上零点的个数为( )A .2021B .4043C .2020D .4044 【答案】B 【解析】(1)(1)f x f x -=+,()(2)f x f x ∴=+,即函数()f x 的周期为2,当[]1,0x ∈-时,()sin()sin()22f x x x πππ=+=-,则当[]0,1x ∈时,()()sin()sin()22f x f x x x ππ=-=--=, 由此可作出函数()f x 与函数e -=xy 的大致图象如下,由图象可知,每个周期内有两个交点, 所以函数((e))xg x f x -=-在区间[]2021,2022-上零点的个数为2021214043⨯+=个.故选:B .【变式5-3】函数()sin 3|sin |,[0,2]f x x x x π=+∈的图象与直线y k =有且仅有两个不同的交点,则k 的取值范围是( )A .[2,2]-B .(1,0)(0,3)-C .(2,4)D .(1,4) 【答案】C【解析】当[0,]x π∈时,()sin 3sin 4sin f x x x x =+=,当(],2x ππ∈时,()sin 3sin 2sin f x x x x =+=-, 所以函数()f x 的图像如图所示,所以函数()f x 的图象与直线y k =有且仅有两个不同的交点时,(2,4)k ∈.故选:C【变式5-4】已知函数()1sin ,0,21cos ,0,2x x f x x x ⎧+<⎪⎪=⎨⎪+≥⎪⎩若()f x 在区间3,2a π⎡⎤-⎢⎥⎣⎦上至少有5个零点,()f x 在区间[],a π-上至多有5个零点,则正数a 的取值范围是( )A .138,63ππ⎡⎤⎢⎥⎣⎦ B .1310,63ππ⎡⎫⎪⎢⎣⎭ C .1910,63ππ⎡⎫⎪⎢⎣⎭ D .819,36ππ⎡⎤⎢⎥⎣⎦【答案】B【解析】因为方程1sin 2x =-在[),0π-上的解为56π-,6π-, 所以当()f x 在区间[],a π-上至多有5个零点时,100.3a π<<因为方程1cos 2x =-在30,2π⎡⎤⎢⎥⎣⎦上的解为23π,43π, 所以当()f x 在区间3,2a π⎡⎤-⎢⎥⎣⎦上至少有5个零点时,136a π-≤-,即136a π≥综上,正数a 的取值范围是1310,63ππ⎡⎫⎪⎢⎣⎭,故选:B。
正弦函数的图像(五点法)

1
0
x -1
0
x
1
-1
二、新知
在研究三角函数的图象和性质时,我们常用弧度制来度量角, 记为χ,表示自变量,用y表示函数值,于是正弦函数表示为
y=sinχ, χ∈R
y
1
0
p
2
π
3p
2π
x
2
-1
y=sinχ,x ∈[ 0, 2π ]
五点法作图 (0,0) (p,0) (2p,0)
y
( p ,1) 2
6
3
因此,换种思考路径,即采用平移线段的方法。
回忆三角函数线:
A'(-1,0)
B(0,1) y
P(cos,sin) N1
x
O M A(1,0)
B'(0,-1)
把单位圆12等分,可以得到对应于
2p 5p π 7p 4 p 3p 5 p
36
6323
y
0
11 p
6y
p pp
6 32 2π 的正弦线
小结:
作正弦函数图象的简图的 方法是:
“五点法”
正弦函数y=sinx的图象 (五点法)
正弦函数:我们常用弧度制来度量角,记为χ, 表示自变量,用y表示函数值,于是正弦函数 表示为y=sinχ, χ∈R
如何来作 正弦函数 的图象呢?
平移正弦线
思考:
时(都,Ⅱ有作)唯出做一相函的对数y值应图和的象它y的值对方,应法,s是i因n1此、p我列们表=1想2、/到2描,当点x而取3、si连n0线p。=任p60意..8给66p ,1) 2
1
x
0p
π
3p
2π
2
2
-1
10 三角函数的图像与性质(1)

10、三角函数的图像与性质(1)教学目标:1、能借助正弦线画出正弦函数的图像,并在此基础上由诱导公式画出余弦函数的图像;2、借助图像理解正(余)弦函数的性质(定义域、值域、周期性、奇偶性).教学过程:一、引入为了更加直观的研究三角函数的性质,先作出它们的图像.怎样作出三角函数的图像?(描点法)二、建构1、 正弦函数的图像由于sin y x =是以2π为周期的函数,故只要先画出在[0,2]π上的图像,然后由周期函数向两边延伸可得整个图像.取2110,,,,,...,,263236x ππππππ=,可计算得110,,022y =-(代数方法),也可以借助单位圆作出sin ,sin ,...63ππ(几何方法)据此可作出一系列点,再用光滑的曲线把这些点连接起来,就得正弦函数sin y x =在[0,2]π上的图像.将sin y x =,[0,2]x π∈的图像向左、右平移(每次2π个单位),得到正弦函数sin ,y x x R =∈的图像,即正弦曲线.说明:如图可见其图像上起着关键作用的点有以下五个:3(0,0),(,1),(,0),(,1),(2,0)22ππππ-,今后我们一般先找出这五个关键点,可画出函数的简图,这种方法叫“五点法” .2、 余弦函数的图像你有什么办法画余弦函数的图像吗?方法一、列表描点法; 方法二,图像变换法.由cos sin()2x x π=+知,由sin y x =图像向左平移2π个单位得到cos y x =的图像.3、 正、余弦函数的性质:(观察图像)(1) 定义域:R(2) 值域:均为[1,1]-(3) 周期性:都是以2π为最小正周期的周期函数(4) 奇偶性:正弦函数是奇函数,余弦函数是偶函数.三、运用例1 用“五点法”画图:sin 2y x =变式:(1)画图 sin2y x =;(2)求sin 2y x =图像对称中心坐标、对称轴方程.例2 求函数x x y sin 21cos lg -+=的定义域.例3 求函数2cos3x y =-的最大值及此时x 的集合.变式: 求函数⎪⎭⎫⎝⎛--=63cos 2πx y 的最大值及此时x 的集合. 四、小结五、作业。
三角函数的图象与性质
-
;
-1
y=cosx
2 3
4 5 4 5
6 x 6 x
五.定义域 、值域及取到最值时相应的x的集合:
-6 -5
-4 -3
复习回顾
-2 -
y y=sinx
1 o
-1
2 3
y
si-n6x的对称-5轴:x
k -4
2-,3对 称点-:2(k
,0);
-
y cosx的对称轴:x k , 对称点:(k ,0);
1.4.1正弦、余弦函数的图象
复习
回顾 三角函数
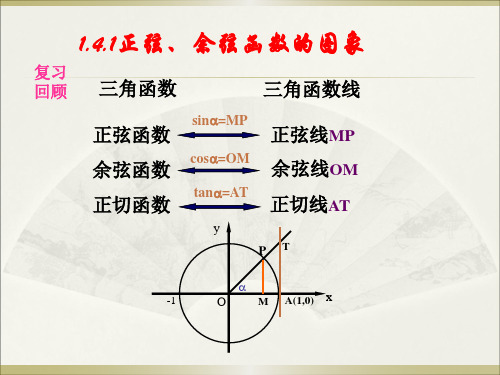
三角函数线
正弦函数 余弦函数 正切函数
sin=MP
正弦线MP cos=OM 余弦线OM tan=AT 正切线AT
y PT
-1
O
M A(1,0) x
正弦、余弦函数的图象
问题:如何作出正弦、余弦函数的图象?
途径:利用单位圆中正弦、余弦线来解决。
描图:用光滑曲线
复习回顾
一.正弦余弦函数的作图: 几何描点法(利用三角函数线) 五点法作简图
二.周期性:
函数y Asin(x )和y Acos(x ),x R的周期T 2 | |
三.奇偶性:
y sin x为奇函数,图像关于原点对称; y cosx为偶函数图像关于y轴对称。
-6 -5
-4 -3
复习回顾 y y=sinx
(0,11)
3
( 2 ,1)
-
(-o12 ,0)
( 2 ,0)
2
( ,-1)
3
线
4
5 6 x
正弦、余弦函数的图象
y
五点画图法
1
(
2
,1)
三角函数图象及应用

函数y =A sin(ωx +φ)的图象及应用1.y =A sin(ωx +φ)的有关概念y=A sin(ωx +φ)(A >0,ω>0),x ∈[0,+∞)振幅 周期 频率 相位 初相A T =2πωf =1T =ω2πωx +φ φ2.如下表所示.x0-φωπ2-φωπ-φω3π2-φω2π-φωωx +φ 0 π2π 3π2 2π y =A sin(ωx +φ)A-A3.函数【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”)(1)作函数y =sin(x -π6)在一个周期内的图象时,确定的五点是(0,0),(π2,1),(π,0),(3π2,-1),(2π,0)这五个点.(×)(2)将函数y =3sin2x 的图象左移π4个单位长度后所得图象的解析式是y =3sin(2x +π4).(×)(3)函数y =sin(x -π4)的图象是由y =sin(x +π4)的图象向右移π2个单位长度得到的.(√)(4)函数y =sin(-2x )的递减区间是(-3π4-k π,-π4-k π),k ∈Z .(×)(5)函数f (x )=sin 2x 的最小正周期和最小值分别为π,0.(√)(6)函数y =A cos(ωx +φ)的最小正周期为T ,那么函数图象的两个相邻对称中心之间的距离为T2.(√)1.(2014·XX)为了得到函数y =sin(2x +1)的图象,只需把函数y =sin2x 的图象上所有的点() A .向左平行移动12个单位长度B .向右平行移动12个单位长度C .向左平行移动1个单位长度D .向右平行移动1个单位长度 答案A解析y =sin2x 的图象向左平移12个单位长度得到函数y =sin2(x +12)的图象,即函数y =sin(2x+1)的图象.2.(2013·XX)函数f (x )=2sin(ωx +φ)(ω>0,-π2<φ<π2)的部分图象如图所示,则ω,φ的值分别是() A .2,-π3B .2,-π6C .4,-π6D .4,π3答案A解析∵34T =5π12-⎝ ⎛⎭⎪⎫-π3,∴T =π,∴ω=2,∴2×5π12+φ=2k π+π2,k ∈Z ,∴φ=2k π-π3,k ∈Z ,又φ∈⎝ ⎛⎭⎪⎫-π2,π2,∴φ=-π3,故选A. 3.设函数f (x )=cos ωx (ω>0),将y =f (x )的图象向右平移π3个单位长度后,所得的图象与原图象重合,则ω的最小值等于() A.13B .3 C .6D .9 答案C解析由题意可知,nT =π3 (n ∈N *),∴n ·2πω=π3(n ∈N *),∴ω=6n (n ∈N *),∴当n =1时,ω取得最小值6.4.设函数f (x )=3sin(ωx +φ)(ω>0,-π2<φ<π2)的图象关于直线x =2π3对称,它的周期是π,则下列说法正确的是________.(填序号) ①f (x )的图象过点(0,32);②f (x )在[π12,2π3]上是减函数;③f (x )的一个对称中心是(5π12,0);④将f (x )的图象向右平移|φ|个单位长度得到函数y =3sin ωx 的图象. 答案①③解析∵周期为π,∴2πω=π⇒ω=2,∴f (x )=3sin(2x +φ),f (23π)=3sin(4π3+φ),则sin(4π3+φ)=1或-1.又φ∈(-π2,π2),4π3+φ∈(5π6,116π),∴4π3+φ=3π2⇒φ=π6, ∴f (x )=3sin(2x +π6).①:令x =0⇒f (x )=32,正确.②:令2k π+π2<2x +π6<2k π+3π2,k ∈Z⇒k π+π6<x <k π+2π3,k ∈Z .令k =0⇒π6<x <2π3,即f (x )在(π6,23π)上单调递减,而在(π12,π6)上单调递增,错误.③:令x =5π12⇒f (x )=3sinπ=0,正确.④:应平移π12个单位长度,错误.题型一函数y =A sin(ωx +φ)的图象及变换例1设函数f (x )=sin ωx +3cos ωx (ω>0)的周期为π. (1)求它的振幅、初相;(2)用五点法作出它在长度为一个周期的闭区间上的图象;(3)说明函数f (x )的图象可由y =sin x 的图象经过怎样的变换而得到的. 解(1)f (x )=sin ωx +3cos ωx=2(12sin ωx +32cos ωx )=2sin(ωx +π3),又∵T =π,∴2πω=π,即ω=2.∴f (x )=2sin(2x +π3).∴函数f (x )=sin ωx +3cos ωx 的振幅为2,初相为π3.(2)令X =2x +π3,则y =2sin ⎝ ⎛⎭⎪⎫2x +π3=2sin X . 列表,并描点画出图象:x-π6 π12 π3 7π12 5π6X 0 π2 π 3π2 2π y =sin X 01 0 -1 0 y =2sin ⎝⎛⎭⎪⎫2x +π32-2(3)方法一把y =sin x 的图象上所有的点向左平移π3个单位长度,得到y =sin ⎝ ⎛⎭⎪⎫x +π3的图象,再把y =sin ⎝ ⎛⎭⎪⎫x +π3的图象上的点的横坐标缩短到原来的12倍(纵坐标不变),得到y =sin ⎝ ⎛⎭⎪⎫2x +π3的图象,最后把y =sin ⎝ ⎛⎭⎪⎫2x +π3上所有点的纵坐标伸长到原来的2倍(横坐标不变),即可得到y=2sin ⎝ ⎛⎭⎪⎫2x +π3的图象.方法二将y =sin x 的图象上每一点的横坐标x 缩短为原来的12倍,纵坐标不变,得到y =sin2x的图象;再将y =sin2x 的图象向左平移π6个单位长度,得到y =sin2⎝ ⎛⎭⎪⎫x +π6=sin ⎝ ⎛⎭⎪⎫2x +π3的图象;再将y =sin ⎝ ⎛⎭⎪⎫2x +π3的图象上每一点的横坐标保持不变,纵坐标伸长为原来的2倍,得到y =2sin ⎝ ⎛⎭⎪⎫2x +π3的图象.思维升华(1)五点法作简图:用“五点法”作y =A sin(ωx +φ)的简图,主要是通过变量代换,设z =ωx +φ,由z 取0,π2,π,32π,2π来求出相应的x ,通过列表,计算得出五点坐标,描点后得出图象.(2)图象变换:由函数y =sin x 的图象通过变换得到y =A sin(ωx +φ)的图象,有两种主要途径:“先平移后伸缩”与“先伸缩后平移”.(1)把函数y =sin(x +π6)图象上各点的横坐标缩短到原来的12(纵坐标不变),再将图象向右平移π3个单位长度,那么所得图象的一条对称轴方程为()A .x =-π2B .x =-π4C .x =π8D .x =π4(2)(2014·XX)将函数y =3sin(2x +π3)的图象向右平移π2个单位长度,所得图象对应的函数()A .在区间[π12,7π12]上单调递减B .在区间[π12,7π12]上单调递增C .在区间[-π6,π3]上单调递减D .在区间[-π6,π3]上单调递增答案(1)A(2)B解析(1)将y =sin(x +π6)图象上各点的横坐标缩短到原来的12(纵坐标不变),得到函数y =sin(2x+π6);再将图象向右平移π3个单位长度,得到函数y =sin[2(x -π3)+π6]=sin(2x -π2),故x =-π2是其图象的一条对称轴方程.(2)y =3sin(2x +π3)的图象向右平移π2个单位长度得到y =3sin[2(x -π2)+π3]=3sin(2x -23π).令2k π-π2≤2x -23π≤2k π+π2得k π+π12≤x ≤k π+712π,k ∈Z ,则y =3sin(2x -23π)的增区间为[k π+π12,k π+712π],k ∈Z . 令k =0得其中一个增区间为[π12,712π],故B 正确.画出y =3sin(2x -23π)在[-π6,π3]上的简图,如图,可知y =3sin(2x-23π)在[-π6,π3]上不具有单调性,故C ,D 错误. 题型二由图象求函数y =A sin(ωx +φ)的解析式例2(1)已知函数f (x )=2sin(ωx +φ)(其中ω>0,|φ|<π2)的最小正周期是π,且f (0)=3,则()A .ω=12,φ=π6B .ω=12,φ=π3C .ω=2,φ=π6D .ω=2,φ=π3(2)已知函数f (x )=A sin(ωx +φ) (A >0,|φ|<π2,ω>0)的图象的一部分如图所示,则该函数的解析式为____________. 答案(1)D(2)f (x )=2sin ⎝⎛⎭⎪⎫2x +π6解析(1)∵f (x )(ω>0,|φ|<π2)的最小正周期为π,∴T =2πω=π,ω=2.∵f (0)=2sin φ=3,即sin φ=32(|φ|<π2),∴φ=π3. (2)观察图象可知:A =2且点(0,1)在图象上, ∴1=2sin(ω·0+φ),即sin φ=12.∵|φ|<π2,∴φ=π6.又∵1112π是函数的一个零点,且是图象递增穿过x 轴形成的零点,∴11π12ω+π6=2π,∴ω=2.∴f (x )=2sin ⎝⎛⎭⎪⎫2x +π6.思维升华根据y =A sin(ωx +φ)+k 的图象求其解析式的问题,主要从以下四个方面来考虑: ①A 的确定:根据图象的最高点和最低点,即A =最大值-最小值2;②k 的确定:根据图象的最高点和最低点,即k =最大值+最小值2;③ω的确定:结合图象,先求出周期T ,然后由T =2πω(ω>0)来确定ω;④φ的确定:由函数y =A sin(ωx +φ)+k 最开始与x 轴的交点(最靠近原点)的横坐标为-φω(即令ωx +φ=0,x =-φω)确定φ.如图为y =A sin(ωx +φ)的图象的一段.(1)求其解析式;(2)若将y =A sin(ωx +φ)的图象向左平移π6个单位长度后得y =f (x ),求f (x )的对称轴方程.解(1)由图象知A =3,以M ⎝ ⎛⎭⎪⎫π3,0为第一个零点,N ⎝ ⎛⎭⎪⎫5π6,0为第二个零点.列方程组⎩⎪⎨⎪⎧ω·π3+φ=0,ω·5π6+φ=π,解得⎩⎪⎨⎪⎧ω=2,φ=-2π3.∴所求解析式为y =3sin ⎝ ⎛⎭⎪⎫2x -2π3.(2)f (x )=3sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x +π6-2π3=3sin ⎝⎛⎭⎪⎫2x -π3,令2x -π3=π2+k π(k ∈Z ),则x =512π+k π2 (k ∈Z ),∴f (x )的对称轴方程为x =512π+k π2 (k ∈Z ).题型三函数y =A sin(ωx +φ)的性质例3(2014·XX 改编)已知函数f (x )=3sin(ωx +φ)(ω>0,-π2≤φ<π2)的图象关于直线x =π3对称,且图象上相邻两个最高点的距离为π. (1)求ω和φ的值;(2)当x ∈[0,π2]时,求函数y =f (x )的最大值和最小值.解(1)因为f (x )的图象上相邻两个最高点的距离为π,所以f (x )的最小正周期T =π,从而ω=2πT=2.又因f (x )的图象关于直线x =π3对称,所以2·π3+φ=k π+π2,k ∈Z , 由-π2≤φ<π2得k =0所以φ=π2-2π3=-π6.综上,ω=2,φ=-π6.(2)由(1)知f (x )=3sin(2x -π6),当x ∈[0,π2]时,-π6≤2x -π6≤56π,∴当2x -π6=π2,即x =π3时,f (x )最大=3;当2x -π6=-π6,即x =0时,f (x )最小=-32.思维升华函数y =A sin(ωx +φ)(A >0,ω>0)的性质(1)奇偶性:φ=k π(k ∈Z )时,函数y =A sin(ωx +φ)为奇函数;φ=k π+π2(k ∈Z )时,函数y =A sin(ωx +φ)为偶函数.(2)周期性:y =A sin(ωx +φ)存在周期性,其最小正周期为T =2πω.(3)单调性:根据y =sin t 和t =ωx +φ(ω>0)的单调性来研究,由-π2+2k π≤ωx +φ≤π2+2k π(k∈Z )得单调增区间;由π2+2k π≤ωx +φ≤3π2+2k π(k ∈Z )得单调减区间.(4)对称性:利用y =sin x 的对称中心为(k π,0)(k ∈Z )来解,令ωx +φ=k π(k ∈Z ),求得其对称中心.利用y =sin x 的对称轴为x =k π+π2(k ∈Z )来解,令ωx +φ=k π+π2(k ∈Z )得其对称轴.已知函数f (x )=A sin(ωx +φ)(x ∈R ,ω,A >0,0<φ<π2)的最大值为2,最小正周期为π,直线x =π6是其图象的一条对称轴.(1)求函数f (x )的解析式;(2)求函数g (x )=f (x -π12)-f (x +π12)的单调递增区间.解(1)∵最小正周期为π. ∴2πω=π.即ω=2.又∵直线x =π6是函数图象的一条对称轴,∴2×π6+φ=k π+π2,k ∈Z ,即φ=k π+π6,k ∈Z .又∵φ∈(0,π2),∴φ=π6.又∵A =2,∴函数f (x )的解析式为f (x )=2sin(2x +π6).(2)g (x )=f (x -π12)-f (x +π12)=2sin[2(x -π12)+π6]-2sin[2(x +π12)+π6]=2sin2x -2sin(2x +π3)=2sin(2x -π3).由2k π-π2≤2x -π3≤2k π+π2,k ∈Z 可得k π-π12≤x ≤k π+512π,k ∈Z .即函数g (x )的单调递增区间是 [k π-π12,k π+512π],k ∈Z .三角函数图象与性质的综合问题典例:(12分)已知函数f (x )=23sin(x 2+π4)·cos(x 2+π4)-sin(x +π).(1)求f (x )的最小正周期.(2)若将f (x )的图象向右平移π6个单位长度,得到函数g (x )的图象,求函数g (x )在区间[0,π]上的最大值和最小值.思维点拨(1)先将f (x )化成y =A sin(ωx +φ)的形式再求周期;(2)将f (x )解析式中的x 换成x -π6,得g (x ),然后利用整体思想求最值.规X 解答解(1)f (x )=23sin(x 2+π4)·cos(x 2+π4)-sin(x +π)=3cos x +sin x [3分]=2sin(x +π3),[5分]于是T =2π1=2π.[6分](2)由已知得g (x )=f (x -π6)=2sin(x +π6),[8分]∵x ∈[0,π],∴x +π6∈[π6,7π6],∴sin(x +π6)∈[-12,1],[10分]∴g (x )=2sin(x +π6)∈[-1,2][11分]故函数g (x )在区间[0,π]上的最大值为2,最小值为-1.[12分] 答题模板解决三角函数图象与性质的综合问题的一般步骤 第一步:(化简)将f (x )化为a sin x +b cos x 的形式. 第二步:(用辅助角公式)构造f (x )=a 2+b 2·(sin x ·aa 2+b2+cos x ·ba 2+b 2).第三步:(求性质)利用f (x )=a 2+b 2sin(x +φ)研究三角函数的性质. 第四步:(反思)反思回顾,查看关键点、易错点和答题规X . 温馨提醒(1)在第(1)问的解法中,使用辅助角公式a sin α+b cos α=a 2+b 2sin(α+φ)(其中tan φ=ba),或a sin α+b cos α=a 2+b 2cos(α-φ)(其中tan φ=ab),在历年高考中使用频率是相当高的,几乎年年使用到、考查到,应特别加以关注. (2)求g (x )的最值一定要重视定义域,可以结合三角函数图象进行求解.方法与技巧1.五点法作图及图象变换问题(1)五点法作简图要取好五个关键点,注意曲线凸凹方向;(2)图象变换时的伸缩、平移总是针对自变量x 而言,而不是看角ωx +φ的变化.2.由图象确定函数解析式由函数y =A sin(ωx +φ)的图象确定A 、ω、φ的题型,常常以“五点法”中的第一个零点⎝ ⎛⎭⎪⎫-φω,0作为突破口,要从图象的升降情况找准第一个零点的位置.要善于抓住特殊量和特殊点. 3.对称问题函数y =A sin(ωx +φ)的图象与x 轴的每一个交点均为其对称中心,经过该图象上坐标为(x ,±A )的点与x 轴垂直的每一条直线均为其图象的对称轴,这样的最近两点间横坐标的差的绝对值是半个周期(或两个相邻对称中心的距离). 失误与防X1.由函数y =sin x 的图象经过变换得到y =A sin(ωx +φ)的图象,如:先伸缩,再平移时,要把x 前面的系数提取出来.2.复合形式的三角函数的单调区间的求法.函数y =A sin(ωx +φ)(A >0,ω>0)的单调区间的确定,基本思想是把ωx +φ看做一个整体.若ω<0,要先根据诱导公式进行转化. 3.函数y =A sin(ωx +φ)在x ∈[m ,n ]上的最值可先求t =ωx +φ的X 围,再结合图象得出y =A sin t 的值域.A 组专项基础训练 (时间:45分钟)1.(2013·XX)将函数y =sin(2x +φ)的图象沿x 轴向左平移π8个单位后,得到一个偶函数的图象,则φ的一个可能取值为() A.3π4B.π4C .0D .-π4 答案B解析把函数y =sin(2x +φ)沿x 轴向左平移π8个单位后得到函数y =sin2⎝ ⎛⎭⎪⎫x +φ2+π8=sin ⎝ ⎛⎭⎪⎫2x +φ+π4为偶函数,则φ的一个可能取值是π4.2.(2013·XX)函数f (x )=sin x cos x +32cos2x 的最小正周期和振幅分别是() A .π,1B .π,2C .2π,1D .2π,2 答案A解析f (x )=sin x cos x +32cos2x =12sin2x +32cos2x =sin ⎝⎛⎭⎪⎫2x +π3.所以最小正周期为π,振幅为1. 故选A.3.已知函数f (x )=2sin(ωx +φ)(ω>0,且|φ|<π2)的部分图象如图所示,则函数f (x )的一个单调递增区间是() A .[-7π12,5π12]B .[-7π12,-π12]C .[-π12,7π12]D .[-π12,5π12]答案D解析由函数的图象可得14T =23π-512π,∴T =π,则ω=2.又图象过点(512π,2),∴2sin(2×512π+φ)=2,∴φ=-π3+2k π,k ∈Z ,∵|φ|<π2.∴取k =0,即得f (x )=2sin(2x -π3),其单调递增区间为[k π-π12,k π+5π12],k ∈Z ,取k =0,即得选项D.4.电流强度I (安)随时间t (秒)变化的函数I =A sin(ωt +φ)(A >0,ω>0,0<φ<π2)的图象如右图所示,则当t =1100秒时,电流强度是()A .-5安B .5安C .53安D .10安 答案A解析由图象知A =10,T 2=4300-1300=1100,∴ω=2πT=100π.∴I =10sin(100πt +φ).⎝ ⎛⎭⎪⎫1300,10为五点中的第二个点, ∴100π×1300+φ=π2.∴φ=π6.∴I =10sin ⎝ ⎛⎭⎪⎫100πt +π6,当t =1100秒时,I =-5安.5.已知函数f (x )=2sin ωx 在区间[-π3,π4]上的最小值为-2,则ω的取值X 围是()A .(-∞,-92]∪[6,+∞)B .(-∞,-92]∪[32,+∞)C .(-∞,-2]∪[6,+∞)D .(-∞,-2]∪[32,+∞)答案D解析当ω>0时,-π3ω≤ωx ≤π4ω,由题意知-π3ω≤-π2,即ω≥32;当ω<0时,π4ω≤ωx ≤-π3ω,由题意知π4ω≤-π2,∴ω≤-2.综上可知,ω的取值X 围是(-∞,-2]∪[32,+∞).6.设偶函数f (x )=A sin(ωx +φ)(A >0,ω>0,0<φ<π)的部分图象如图所示,△KLM 为等腰直角三角形,∠KML =90°,KL =1,则f (16)的值为________.答案34解析取K ,L 中点N ,则MN =12,因此A =12.由T =2得ω=π.∵函数为偶函数,0<φ<π,∴φ=π2,∴f (x )=12cosπx ,∴f (16)=12cos π6=34.7.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数y =a +A cos ⎣⎢⎡⎦⎥⎤π6(x -6)(x =1,2,3,…,12,A >0)来表示,已知6月份的月平均气温最高,为28℃,12月份的月平均气温最低,为18℃,则10月份的平均气温值为________℃. 答案20.5 解析由题意得⎩⎨⎧ a +A =28,a -A =18,∴⎩⎨⎧a =23,A =5,∴y =23+5cos ⎣⎢⎡⎦⎥⎤π6(x -6),当x =10时,y =23+5×⎝ ⎛⎭⎪⎫-12=20.5.8.已知函数f (x )=cos x sin x (x ∈R ),给出下列四个命题: ①若f (x 1)=-f (x 2),则x 1=-x 2; ②f (x )的最小正周期是2π; ③f (x )在区间[-π4,π4]上是增函数;④f (x )的图象关于直线x =3π4对称.其中真命题是________. 答案③④解析f (x )=12sin2x ,当x 1=0,x 2=π2时,f (x 1)=-f (x 2),但x 1≠-x 2,故①是假命题; f (x )的最小正周期为π,故②是假命题;当x ∈[-π4,π4]时,2x ∈[-π2,π2],故③是真命题;因为f (3π4)=12sin 32π=-12,故f (x )的图象关于直线x =34π对称,故④是真命题.9.已知函数f (x )=cos x ·cos(x -π3).(1)求f (2π3)的值;(2)求使f (x )<14成立的x 的取值集合.解(1)f (2π3)=cos 2π3·cos π3=-cos π3·cos π3=-(12)2=-14.(2)f (x )=cos x cos(x -π3)=cos x ·(12cos x +32sin x )=12cos 2x +32sin x cos x =14(1+cos2x )+34sin2x =12cos(2x -π3)+14. f (x )<14等价于12cos(2x -π3)+14<14,即cos(2x -π3)<0,于是2k π+π2<2x -π3<2k π+3π2,k ∈Z .解得k π+5π12<x <k π+11π12,k ∈Z .故使f (x )<14成立的x 的取值集合为{x |k π+5π12<x <k π+11π12,k ∈Z }.10.(2014·XX)已知函数f (x )=cos x (sin x +cos x )-12.(1)若0<α<π2,且sin α=22,求f (α)的值;(2)求函数f (x )的最小正周期及单调递增区间. 解方法一(1)因为0<α<π2,sin α=22,所以cos α=22. 所以f (α)=22×(22+22)-12=12. (2)因为f (x )=sin x cos x +cos 2x -12=12sin2x +1+cos2x 2-12 =12sin2x +12cos2x =22sin(2x +π4), 所以T =2π2=π.由2k π-π2≤2x +π4≤2k π+π2,k ∈Z ,得k π-3π8≤x ≤k π+π8,k ∈Z . 所以f (x )的单调递增区间为[k π-3π8,k π+π8],k ∈Z .方法二f (x )=sin x cos x +cos 2x -12=12sin2x +1+cos2x 2-12 =12sin2x +12cos2x =22sin(2x +π4). (1)因为0<α<π2,sin α=22,所以α=π4,从而f (α)=22sin(2α+π4)=22sin 3π4=12.(2)T =2π2=π.由2k π-π2≤2x +π4≤2k π+π2,k ∈Z ,得k π-3π8≤x ≤k π+π8,k ∈Z . 所以f (x )的单调递增区间为[k π-3π8,k π+π8],k ∈Z .B 组专项能力提升 (时间:20分钟)11.将函数y =sin(x +φ)的图象F 向左平移π6个单位长度后得到图象F ′,若F ′的一个对称中心为⎝ ⎛⎭⎪⎫π4,0,则φ的一个可能取值是() A.π12B.π6C.5π6D.7π12 答案D解析图像F ′对应的函数y =sin ⎝ ⎛⎭⎪⎫x +π6+φ, 则π4+π6+φ=k π,k ∈Z ,即φ=k π-5π12,k ∈Z , 当k =1时,φ=7π12,故选D.12.已知A ,B ,C ,D 是函数y =sin(ωx +φ)(ω>0,0<φ<π2)一个周期内的图象上的四个点,如图所示,A (-π6,0),B 为y 轴上的点,C 为图象上的最低点,E 为该函数图象的一个对称中心,B 与D 关于点E 对称,CD →在x 轴上的投影为π12,则ω,φ的值为()A .ω=2,φ=π3B .ω=2,φ=π6C .ω=12,φ=π3D .ω=12,φ=π6答案A解析因为CD →在x 轴上的投影为π12,又点A (-π6,0),所以函数的四分之一个最小正周期为π6+π12=π4.即函数的最小正周期为π,故ω=2ππ=2. 又点A (-π6,0)是处于递增区间上的零点,所以2×(-π6)+φ=2k π(k ∈Z ),则φ=2k π+π3(k ∈Z ).又因为0<φ<π2,所以φ=π3.故选A.13.(2014·XX)已知函数f (x )=sin(ωx +φ) (ω>0,-π2≤φ≤π2)的图象上的两个相邻的最高点和最低点的距离为22,且过点⎝ ⎛⎭⎪⎫2,-12,则函数的解析式为_________________________.答案f (x )=sin ⎝⎛⎭⎪⎫πx 2+π6解析据已知两个相邻最高点和最低点距离为22,可得⎝ ⎛⎭⎪⎫T 22+(1+1)2=22,解得T =4,故ω=2πT =π2,即f (x )=sin ⎝ ⎛⎭⎪⎫πx 2+φ,又函数图象过点⎝ ⎛⎭⎪⎫2,-12,故f (2)=sin(π+φ)=-sin φ=-12,又-π2≤φ≤π2,解得φ=π6,故f (x )=sin ⎝ ⎛⎭⎪⎫πx 2+π6.14.(2014·XX)某实验室一天的温度(单位:℃)随时间t (单位:h)的变化近似满足函数关系:f (t )=10-3cos π12t -sin π12t ,t ∈[0,24).(1)XX 验室这一天的最大温差;(2)若要XX 验室温度不高于11℃,则在哪段时间实验室需要降温? 解(1)因为f (t )=10-2(32cos π12t +12sin π12t ) =10-2sin(π12t +π3),又0≤t <24,所以π3≤π12t +π3<7π3,-1≤sin(π12t +π3)≤1.当t =2时,sin(π12t +π3)=1;当t =14时,sin(π12t +π3)=-1.于是f (t )在[0,24)上的最大值为12,最小值为8.故实验室这一天最高温度为12℃,最低温度为8℃,最大温差为4℃.(2)依题意,当f (t )>11时实验室需要降温. 由(1)得f (t )=10-2sin(π12t +π3),故有10-2sin(π12t +π3)>11,即sin(π12t +π3)<-12.又0≤t <24,因此7π6<π12t +π3<11π6,即10<t <18.故在10时至18时实验室需要降温.15.已知函数f (x )=3sin ωx ·cos ωx +cos 2ωx -12(ω>0),其最小正周期为π2.(1)求f (x )的表达式;(2)将函数f (x )的图象向右平移π8个单位长度,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y =g (x )的图象,若关于x 的方程g (x )+k =0在区间[0,π2]上有且只有一个实数解,XX 数k 的取值X 围. 解(1)f (x )=3sin ωx ·cos ωx +cos 2ωx -12=32sin2ωx +cos2ωx +12-12=sin(2ωx +π6), 由题意知f (x )的最小正周期T =π2,T =2π2ω=πω=π2,所以ω=2,所以f (x )=sin(4x +π6).(2)将f (x )的图象向右平移π8个单位长度后,得到y =sin(4x -π3)的图象;再将所得图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到y =sin(2x -π3)的图象,所以g (x )=sin(2x -π3),因为0≤x ≤π2,所以-π3≤2x -π3≤2π3,所以g (x )∈[-32,1] 又g (x )+k =0在区间[0,π2]上有且只有一个实数解,即函数y =g (x )与y =-k 在区间[0,π2]上有且只有一个交点,由正弦函数的图象可知-32≤-k<32或-k=1,解得-32<k≤32或k=-1,所以实数k的取值X围是(-32,32]∪{-1}.。
三角函数的图象、性质及应用(高中数学知识点讲解)

(5)不能认为y=tan
x在定义域上为增函数,应在区间
kπ-
π 2
,kπ
+
π 2
(k∈Z)内
为增函数.
知能拓展
考法一 关于三角函数图象的问题
例1 (1)(2018广东茂名化州二模,9)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<
φ<π)的部分图象如图所示,且f(α)=1,α∈
求φ及ω,从而
得到f(x)的解析式,由f(α)=1求α,进而得cos
2α
+
5π 6
.
A = 5,
(2)①根据已知表格中的数据可得方程组
π 3
ω
+
φ
=
π 2
,
解之可得函数f(x)的
5π 6
ω
+
φ
=
3π 2
,
解析式,进而可补全表格.
②由①并结合函数图象平移可得,g(x)=5sin
2
x
+
2θ -
π 3
-2x
实质上是y=tan
x与y=
π 3
-2x的复合,应
按复合函数单调性求解.
方法总结 三角函数的单调性问题的常见类型及解题策略
1.已知三角函数解析式求单调区间
(1)求函数的单调区间应遵循简单化原则,将解析式进行化简,并注意复合
函数单调性规律“同增异减”.
(2)求形如y=Asin(ωx+φ)或y=Acos(ωx+φ)(其中ω>0)的单调区间时,要视“ωx
2π ω
=4×
7π 12
-
π 3
=π,得ω=2,故f(x)=3sin(2x+φ),将
