举例说明多层次模糊综合评价的步骤,并画出其层次结构图。
12 模糊综合评价模型

二 模糊综合评价模型模糊综合评判方法,是一种运用模糊数学原理分析和评价具有“模糊性”的事物的系统分析方法。
它是一种以模糊推理为主的定性与定量相结合、精确与非精确相统一的分析评价方法。
由于这种方法在处理各种难以用精确数学方法描述的复杂系统问题方面所表现出的独特的优越性,近年来已在许多学科领域中得到了十分广泛的应用。
2.1 模糊综合评判模型2.1.1单层次模糊综合评判模型给定两个有限论域U={u 1,u 2,…,um } (1) V={v 1,v 2,…,v n } (2)(1)式中,U 代表所有的评判因素所组成的集合;(2)式中,V 代表所有的评语等级所组成的集合。
如果着眼于第i(i=1,2,…,m)个评判因素u i ,其单因素评判结果为R i =[r i1,r i2,…,r in ],则m 个评判因素的评判决策矩阵为11112122122212n n m m m mn R r r r R r r r R R r r r ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦(3) 就是U 到V 上的一个模糊关系。
如果对各评判因数的权数分配为:1,2,,m A a a a ⎡⎤=⎣⎦(显然,A 是论域U 上的一,个模糊子集,且101,1mi i i a a =≤≤=∑)则应用模糊变换的合成运算,可以得到论域V 上的一个模糊子集,即综合评判结果:1,2,,n B A R b b b ⎡⎤=⨯=⎣⎦ (4)2.1.2多层次模糊综合评判模型在复杂大系统中,需要考虑的因素往往是很多的,而且因素之间还存在着不同的层次。
这时,应用单层次模糊综合评判模型就很难得出正确的评判结果。
所以,在这种情况下,就需要将评判因素集合按照某种属性分成几类,先对每一类进行综合评判,然后再对各类评判结果进行类之间的高层次综合评判。
这样,就产生了多层次模糊综合评判问题。
多层次模糊综合评判模型的建立,可按以下步骤进行:(1)对评判因素集合U ,按某个属性,将其划分成m 个子集,使它们满足:1()mi i ij U UU U i j =⎧=⎪⎨⎪⋂=Φ≠⎩∑ (5)这样,就得到了第二级评判因素集合: U={U 1,U 2,…,U m } (6)在(6)式中,U i ={U ik }(i=1,2,…,m ;k=1,2,…,nk)表示子集U i 中含有n k 个评判因素。
模糊综合评价法的步骤

模糊综合评价法的步骤
模糊综合评价法是一种基于模糊数学的多因素评价方法,它通过
模糊集合理论和模糊逻辑推理,对多个因素进行综合评价。
模糊综合
评价法的主要步骤如下:
1. 确定评价因素和评价等级:首先需要确定评价对象的因素和评
价等级,因素可以是多个,评价等级可以是定性的或定量的。
2. 建立模糊关系矩阵:根据评价因素和评价等级之间的关系,建
立模糊关系矩阵。
模糊关系矩阵是一个二维矩阵,其中每行表示一个
因素,每列表示一个评价等级。
3. 确定权重向量:根据各个因素的重要性,确定每个因素的权
重。
权重向量是一个一维向量,其中每个元素表示一个因素的权重。
4. 进行模糊合成:根据模糊关系矩阵和权重向量,进行模糊合成
得到综合评价结果。
模糊合成可以采用不同的方法,如模糊加权平均法、模糊综合评判法等。
5. 进行综合评价:根据模糊合成的结果,进行综合评价。
综合评
价结果可以是一个数值或一个模糊集合。
需要注意的是,模糊综合评价法的应用需要结合具体的问题和数据进行分析和处理,同时需要对模糊数学的基本理论和方法有一定的了解。
第十三章2层次分析法及模糊综合评价PPT课件

• 构造成对比较阵是数量依据,应由经验丰富、判 断力强的专家给出。
例1 国家 实力分析
国民 收入
例2 工作选择
国家综合实力
军事 力量
科技 水平
社会 稳定
美、俄、中、日、德等大国 工作选择
贡
收
发
声
~ n
(k1)
1 wi
n w i1
(k) i
3. 特征向量作为权向量——成对比较的多步累积效应
问题 一致阵A, 权向量w=(w1,…wn)T, aij=wi/wj
A不一致, 应选权向量w使wi/wj与 aij相差 尽量小(对所有i,j)。
用拟合方法确定w
2
n
min
wi (i1,,n) i1
n j1aij
任一元素xi,再考虑此元素属于集合 A 的可能
性。
A A a 1 A a 2 A a iA a n
a 1
a 2
a i
a n
模糊数学
(三)截集
模糊集合的 截集是指 X 中对 A 的隶属 度不小于 的一切元素组成的普通集合。
其定义为:
对于给定的实数 (01),定义
A { x | A ( x ) }
用成对比较法和1~9尺度,构造各层对上一层每一因素的 成对比较阵。
3)计算权向量并作一致性检验
对每一成对比较阵计算最大特征根和特征向量,作一致性 检验,若通过,则特征向量为权向量。
4)计算组合权向量(作组合一致性检验*)
组合权向量可作为决策的定量依据。
二. 层次分析法的广泛应用
• 应用领域:经济计划和管理,能源政策和分配, 人才选拔和评价,生产决策,交通运输,科研选题, 产业结构,教育,医疗,环境,军事等。
模糊综合评价法举例
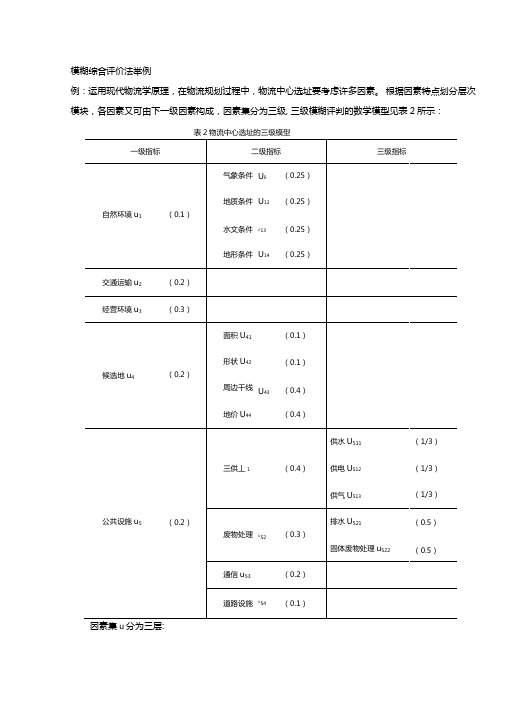
模糊综合评价法举例例:运用现代物流学原理,在物流规划过程中,物流中心选址要考虑许多因素。
根据因素特点划分层次模块,各因素又可由下一级因素构成,因素集分为三级, 三级模糊评判的数学模型见表2所示:表2物流中心选址的三级模型一级指标二级指标三级指标气象条件U li (0.25)地质条件U12 (0.25)自然环境u1(0.1)水文条件U13 (0.25)地形条件U14 (0.25)交通运输u2(0.2)经营环境u3(0.3)面积U41(0.1)形状U42 (0.1)候选地u4(0.2)周边干线U(0.4)43地价U44 (0.4)供水U511(1/3)三供丄1 (0.4)供电U512 (1/3)供气U513 (1/3)公共设施u5(0.2)排水U521(0.5)废物处理U52 (0.3)固体废物处理u522(0.5)通信u53(0.2)道路设施U54 (0.1)因素集u分为三层:第一层为U = di,U2,U3,U4,U5?第二层为 U^'.U ii,U i2,U13,U14 /;U^'.U41,U42,U43,U44^U^'.U51,U52,U53,U54?第三层为U5^ tU511 ,U512, U51^f ;U5^ ~ L U521,U522 p?假设某区域有8个候选地址,决断集V X代B,C,D,E,F,G,H?代表8个不同的候选地址,数据进行处理后得到诸因素的模糊综合评判如表3所示。
表3某区域的模糊综合评判⑴分层作综合评判U51 -山511川512山513?,权重阳-「1/ 3,1/ 3,1/ 3},由表3对丄仆丄②比^的模糊评判构成的单因素评判矩阵:'0.60 0.71 0.77 0.60 0.82 0.95 0.65 0.76"0.60 0.71 0.70 0.60 0.80 0.95 0.65 0.76卫.91 0.90 0.93 0.91 0.95 0.93 0.81 0.89』用模型Mg •)(矩阵运算)计算得:B51讥砥=(0.703,0.773,0.8,0.703,0.857,0.943,0.703,0.803)类似地:B52=乓2 R52 = (0.895,0.885,0.785,0.81,0.95,0.77,0.775, 0.77)‘0.7030.773 0.8 0.703 0.857 0.943 0.703 0.803、B5 =A5°R5 =(0.4 0.3 0.2 0.1)°0.895 0.885 0.785 0.81 0.95 0.77 0.775 0.770.81 0.94 0.89 0.60 0.65 0.95 0.95 0.89I 0.90 0.60 0.92 0.60 0.60 0.84 0.65 0.81 j =(0.802,0.823,0.826,0.704,0.818,0.882,0.769,0.811)巾.60 0.95 0.60 0.95 0.95 0.95 0.95 0.95'B4=代=(0.1 0.1 0.4 0.4) °0.60 0.69 0.92 0.92 0.87 0.74 0.89 0.95 0.95 0.69 0.93 0.85 0.60 0.60 0.94 0.78 ©.750.60 0.80 0.93 0.84 0.84 0.60 0.80 ;=(0.8,0.68,0.844,0.899,0.758,0.745,0.8,0.822)*0.91 0.85 0.87 0.98 0.79 0.60 0.60 0.95' B, f QR =(0.25 0.25 0.25 0.25)。
模糊综合评判方法在教师综合素质评价中的应用

分为类或层, 每类按单级模糊综合评判方法得到一个 评判结果, 再对所得的单级评判结果进行综合评估,
即可得到最终结果.
多层次模糊综合评判的步骤是: ( 1) 对因素集合 U 按属性划分为若干子集. 设 U
= { U1, U2, , Un} , 划分 U = { U1, U2, , Uk} , 且满
k
# 足 Ui = U, Ui ∃ Uj = , i % j . 第二层次因素子集 i= 1
, ak ) ( 这里 k = 4) 和 A i ( ai1 , ai2 , , aini ) , ( i = 1, 2, 3, 4) ( 这里 ni 均为 4) . 其次, 用二层次综合评价模型, 计算结构性指标 U i ( i = 1, 2, 3, 4) 的综合评价向量 B = A R. 评语集 V = { v1 , v2 , v3 , v4 } , v1 表示优秀, v2 表示合格, v3 表示基本合格, v4 表示不合格. 取评语 v j 相应分值, 用模糊向量单值化方法, 即可计算出被 评教师的综合评分值. 2. 1 确定准则层权重
根据专家意见, 用 AH P 方法将分别确定出主准 则层、子准则层各评价准则的重要程度排序.
用 1 ~ 9 标度, 通过两两比较, 建立正互反判断 矩阵, 再由特 征根法计 算出主准 则层( Ui 对目标 层 U) 的 权 重 向 量 为 A = ( 0 4011, 0 3587, 0 1713,
2005 年第 3 期
B
∋ 3
=
A3
R
∋ 3
=
( 0. 0831,
0. 4313,
0. 4313, 0. 4) ,
B
∋ 4
=
A4
R
模糊综合评价法 (2)

模糊综合评价法
模糊综合评价法是一种常用的多指标决策方法,它将模糊
数学理论应用于决策分析中。
该方法通过将不确定性和主
观性的因素引入评价过程,可以更好地处理实际决策问题。
模糊综合评价法的步骤如下:
1. 确定评价指标:根据具体的决策问题,确定相应的评价
指标,并对指标进行量化。
2. 确定评价等级:根据实际情况,确定评价指标的评价等级,一般分为五个等级:优秀、良好、一般、较差、差。
3. 构建模糊矩阵:根据评价指标的评价等级,构建模糊矩阵,每个指标对应一行,每个评价等级对应一列。
4. 模糊评价:对每个指标,根据实际情况进行模糊评价,
用模糊数表示,如“优秀”可以表示为(1,0,0,0,0)。
5. 模糊矩阵加权求和:对于每个指标,乘以其权重,然后
将所有指标的结果相加,得到综合评价值。
6. 模糊综合评价结果的解模糊化:可以使用模糊数学中的
聚合函数(如最大值法、最小值法等)将模糊综合评价结
果转化为确定性的数值。
7. 结果分析和决策:根据模糊综合评价结果进行结果分析,做出决策。
模糊综合评价法能够综合考虑多个指标的权重和评价等级,并且允许模糊的评价结果。
在实际决策问题中,它能够提
供更全面和准确的评价结果,有很广泛的应用领域,如企业绩效评价、项目评估和选优、人才选拔等。
综合评价方法 - 层次分析法加模糊评价方法

从数学角度来看,身边的现象可划分为:
1.确定性现象:如水加温到100 C就沸腾,这种现象的规 律性靠经典数学去刻画; 2.随机现象:如掷筛子,观看那一面向上,这种现象的 规律性靠概率统计去刻画; 3.模糊现象:如 “今天天气很热”,“某人个头 高”,…等等。 这些语言的准确性就要用模糊数学去刻画。
7
(4)层次分析法的优缺点
优点: 1 系统性——将对象视作系统,按照分解、比较、 判断、综合的思维方式进行决策——系统分析(与机 理分析、测试分析并列); 2 实用性——定性与定量相结合,能处理传统的 优化方法不能解决的问题; 3 简洁性——计算简便,结果明确,便于决策者 直接了解和掌握。 缺点: 1. 不能为决策提供新方案 2. 定量数据较少,定性成分多,不易令人信服 3. 指标过多时数据统计量大,且权重难以确定 4. 特征值和特征向量的精确求法比较复杂
可以看到两种方法求出的权重相差不大 同理可以求出准则层各判断矩阵的权重向量
17
层次总排序:在获得同一层次各要素之间的相对重要 度后,自上而下计算各级要素相对总体的综合重要度。 即针对上一层次而言,逐层计算本层次所有元素重要 性的权重。 Wi w j vij 综合重要度: j
得到的层次总排序的权值向量是否可以被满意接受, 需要进行一致性检验。 但在实际应用中,整体一致性的检验常常不必进行。 主要原因是对整体进行考虑是很困难的;另外,若单 层次排序下具有满意一致性,而整体不具有满意一致 性时,判断矩阵的调整非常困难。因此,一般情况下 可以不进行整体一致性检验。
安全系统工程学
综合评价方法
一、层次分析法(AHP)
二、模糊综合评价法
2
综合评价法 之层次分析法
一、层次分析法
多级模糊综合评价模型

多级模糊综合评价模型
多级模糊综合评价模型是一种常见的评价方法,它可以用于对复杂问题进行综合评价。
它的基本思想是将问题分解为多个层次,每个层次都有多个评价指标,通过模糊化处理,将各个指标的权重进行综合,得出最终的评价结果。
在实际应用中,多级模糊综合评价模型被广泛应用于企业管理、市场调研、经济决策等领域。
多级模糊综合评价模型的基本步骤包括:
1. 确定评价层次结构:将复杂问题分解为多个层次,每个层次都有多个评价指标。
2. 确定每个指标的权重:通过专家调查、问卷调查等方法,确定每个指标的重要程度。
3. 进行模糊化处理:将各个指标的权重进行模糊化处理,得出各个指标之间的关系。
4. 进行综合评价:通过模糊综合运算,得出最终的评价结果。
多级模糊综合评价模型的优点在于它可以处理复杂问题,并且能够考虑到不同指标之间的相互影响。
但是,它也存在一些缺点,比如需要大量的数据和专家意见,而且模型的建立比较复杂。
在实际应用中,多级模糊综合评价模型可以用于企业管理中的绩效评估、市场调研中的产品评价、经济决策中的投资决策等方面。
例如,在企业管理中,可以将企业分解为多个部门,每个部门再分解为多个岗位,通过对各个岗位的绩效指标进行评估,得出整个企业的绩效水平。
在市场调研中,可以将产品分解为多个方面,如性能、价格、外观等方面进行评估,得出产品在市场上的竞争力。
在经济决策中,可以将投资项目分解为多个方面,如投资风险、收益率等方面进行评估,得出是否进行投资的决策。
总之,多级模糊综合评价模型是一种非常实用的评价方法,在实际应用中有着广泛的应用前景。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
举例说明多层次模糊综合评价的步骤,并画出其层次
结构图。
模糊和综合评价法的步骤包括:
1、模糊综合评价指标的构建是进行综合评价的基础,评价指标的选取适宜,将直接影响综合评价的准确性,进行评价指标的构建应广泛涉猎与该评价指标系统行业资料或者相关的法律法规;
2、采用构建好权重向量通过专家经验法或者AHP层次分析法构建好权重向量;
3、构建评价矩阵建立适合的隶属函数,从而构建好评价矩阵;
4、评价矩阵和权重的合成采用适合的合成因子对其进行合成和对结果向量进行解释。
1、评价指标体系的建立
企业作为一个社会生产单位,其质量经济效益最终表现在产品质量和经济效益两个方面,而每个方面又由若干评价指标所决定。
相应地,评价指标集分为两个层次:第一层,总目标因素集;第二层,子目标因素集和子目标因素集。
2、评价集的确定
本模型的评语共分五个等级。
3、权重的确定
在进行模糊综合评价时,权重对最终的评价结果会产生很大的影响,权重选择的合适与否直接关系到模型的成败。
确定权重的方法有很多,如专家估计法、层次分析(AHP)法。
在综合有关专家意见
的基础上,本模型最终的权重确定结果如下:
权重确定的依据有下列三条:
1)产品质量和经济效益在综合评价系统中占有同等重要的地位,轻视任何一方对企业的发展都不利。
2)产品质量的决定权在用户而不是生产企业,只有用户满意的产品才是真正高质量的产品。
3)生产者在追求自身经济效益的同时,要兼顾消费者和社会的经济效益。
