高等固体物理学
高三物理知识点梳理固体物理学与材料科学

高三物理知识点梳理固体物理学与材料科学高三物理知识点梳理—固体物理学与材料科学固体物理学与材料科学是物理学的重要分支,涉及到固体物质的结构、性质和应用。
本文将对高三物理知识点进行梳理,主要集中于固体物理学与材料科学相关的内容。
通过对这些知识点的了解,可以加深对固体物理学与材料科学的理解,帮助提高物理学的学习效果。
1. 固体的结构与性质固体物质的结构与性质是固体物理学的核心内容,了解固体的结构有助于理解其性质和力学行为。
1.1. 晶体结构:晶体是由具有周期性排列的原子、离子或分子组成的,具有长程有序性的固体。
晶体结构包括晶格和晶胞两个概念。
晶格是原子、离子或分子排列的空间周期性结构,晶胞是晶体结构的最小单位。
1.2. 非晶体结构:非晶体是没有长程有序结构的固体,其结构具有无规则性。
与晶体相比,非晶体的性质较为复杂,难以确定其具体结构。
1.3. 晶体缺陷:晶体中存在各种类型的缺陷,包括点缺陷、线缺陷和面缺陷。
这些缺陷不仅影响晶体的结构,还对其性质和性能产生重要影响。
1.4. 物质的力学性质:固体物质具有弹性、塑性和脆性等不同的力学性质。
这些性质与晶体结构和缺陷密切相关,通过对固体物质的结构和性质的研究,可以深入了解物质的力学行为。
2. 材料科学的应用材料科学是研究材料组成、结构和性能以及其应用的学科。
以下是几个常见的材料科学应用领域。
2.1. 金属材料:金属材料是最常见的工程材料之一,其研究重点包括金属的合金化、强化、热处理等方面,以提高材料的力学性能。
2.2. 半导体材料:半导体材料广泛应用于电子器件中,如晶体管、太阳能电池等。
研究半导体材料的性质和结构有助于提高电子器件的性能和效率。
2.3. 高分子材料:高分子材料具有广泛的应用领域,如塑料、橡胶、合成纤维等。
研究高分子材料的结构和性质,可以改善材料的加工性能和使用性能。
2.4. 纳米材料:纳米材料是指尺寸在纳米级别的材料,具有独特的物理、化学和生物学性质。
高等固体物理(基泰尔)Su11

the Bloch T3/2 law experimentally confirmed
NEUTRON MAGNETIC SCATTERING
An x-ray photon sees the spatial distribution of electronic charge, whether the charge density is magnetized or unmagnetized. A neutron sees two aspects of a crystal: the distribution of nuclei and the distribution of electronic magnetization.
金属中自由电子在磁场方向的运动保持不变,而在垂直磁场的平面内电 子作圆周运动。此圆周运动产生的磁矩与外磁场方向相反,具有抗 磁性。
Paramagnetism
1. Atoms, molecules, and lattice defects possessing an odd number of electrons. Examples: free sodium atoms; NO; F centers in alkali halides
FERROMAGNETIC DOMAINS
In weak fields the volume of domains favorably oriented with respect to the field increases at the expense of unfavorably oriented domains; In strong fields the domain magnetization rotates toward the direction of the field. coercivity: Hc Br: the remanence induction Bs: the saturation induction B--- H or M----H B=0(H+M)
高等固体物理

选择矢量势
A(0,B,x0)
波函数为
(x,y)eik yy (x)
2 m 2 d d22 x1 2m c 2(xlc 2ky)2eE (xx)(x)
1
lc
c eB
2
.
经典回旋半径
解为:
i(E)
(i
1 2
)
c
eE (lc2k y
eE
2
m
2 c
)
i ( x,
y)
( x ( ik y y )
如 Fermi 能级处于能隙中
无外磁场,
g(E
)=
m 2 2
加磁场 Landau 能级
GH
ec
n ( F ) B
简并度 如电子占据
c g ( E )
eB hc
i 个 Landau 能级:
n ieB hc
1
h
R H (i) G H e 2i
.
应用: (a)电阻标准
自 19年 90起,h 电 25 阻 .80 1 标 (精 6 2 准 度 2 1 : 0 ~ 8) e2
xx
xx ,
2
2
xx xy
xy
xy
2
2
xx xy
如果 xy 0 , 则当 xx 为0时 xx 也为0.
.
另一方面
xynBeccxtx
由此, 当 xx 0 时, jx xyEy , xy 为霍尔电导
H
x
y
nec B
jy yx ExxE yx
在量子力学下(E沿x方向)
H 1 (PeA )2eEx 2m c
Room-Temperature Quantum Hall Effect in Graphene
高等固体物理学

高等固体物理学
高等固体物理学是研究物质的结构和性质的分支学科。
在这一领
域中,研究的对象是材料的晶体结构、电子结构以及它们在宏观和微
观层面上的物理性质。
在高等固体物理学中,晶体结构是一个非常重要的概念。
晶体是
由原子、分子或离子在周期性排列的模式中组成的。
这种排列方式决
定了晶体的物理性质。
晶体的晶格参数、晶体的空间群、晶体的空间
分组、晶体的晶格动力学,这些都是从晶体结构中获得的信息。
电子结构是高等固体物理学的另一个重要的研究领域。
电子结构
描述了电子在晶体中的分布方式。
通过研究电子结构,可以确定材料
的电导率、磁性以及光学性质。
一般来说,具有多余电子的物质是导体;带有缺电子的是半导体,而没有多余电子或缺电子的是绝缘体。
因此,研究电子结构可以为材料在各种应用中提供指导意义。
在高等固体物理学中还有一个非常重要的课题,那就是物理性质。
各种物理性质,如热容、热导率、电阻率、电荷输运,都取决于材料
的电子结构和晶体结构。
通过对这些性质的研究,可以理解材料在各
种条件下的行为,这对于研究材料的应用具有重要的意义。
总之,高等固体物理学在研究物质的结构和性质方面具有非常重
要的地位。
它为我们提供了深入了解和利用材料的基础平台。
只有深
入地了解物质的基本特性,才能更好地从中挖掘出各种实际应用。
高等固体物理第五章晶格振动与晶体热学性质

一维单原子链模型的振动既简单可解,又能较全面说明晶格振
动的特点。二维、三维振动的特点由一维结论推广得到。 一个
一维单原子链可以看作一个一维简单晶格。并满足三个假设,
(1)假定原子质量为m;
(2)原子限定在原子链方向运动, 偏离格点的位移用μn, μn+1…
表示;
(3)假定只考虑最近邻原子的相互作用。
。分别把上述两微分方程相加和相减,得:
d2(xdat2
xb)
k m(xa
xb
)
d2(xa dt2
xb
)
( k m
2K m )(xa
xb
)
Beihang University
2021/3/9
* 简正坐标和简正频率
d 2 q1 dt 2
k m
q1
d
2
q
2
dt 2
( k m
2K m
)q2
qq12
在理想情况下,不能脱离晶体格点平衡位置,晶格振动是在平衡位 置附近的微小振动。
Beihang University
2021/3/9
§5。2 一维单原子链
前面给出的简正坐标和简谐近似仅仅是解决问题的总的思 路,但真正求解晶格的振动模是很复杂的事。比如:要了解晶 格振动的物理模型、特征等。真正从微观结构导出力常数是固 体理论的内容,现在我们给出一种最简单的情况来讨论:一维 单原子链模型。
2021/3/9
原子的运动方程
只考虑相邻原子的作用,第n 个原子受到的作用力
大学固体物理ppt
绪 论:固体物理学应用
聚变发电
能源危机:
化石能源:2050石油枯竭,煤炭,可燃冰; 太阳能;风能;海洋能;核能:裂变和聚变
东方超环(EAST)
1.65亿元人民币。 韩国3亿美元, 美国5.7亿美元。
ITER
100亿美元
量子计算机(摩尔定律18月 P4,2000)
速度(大数质因子分解)100亿年 vs 30秒 解密 量子隐形传输
布拉伐格子 + 基元 = 晶体结构
一、布拉伐格子 → 表征了晶格的周期性
理想晶体:可看成是由完全相同的基本结构单元 (基元)在空间作周期性无限排列构成 单个原子或离子或若干个原子的集团
① 格点:代表基元中空间位置的点称为格点 一切格点是等价的 — 每个格点的周围环 境相同 → 因为一 切基元的组成,位相和取 向都相同!
, 为 一组基矢 Rl l1a1 l2a2 l3a3 a1, a2 , a3
x
1
3
二维布拉伐格子几种可能的基矢和原胞取法
二维晶格的晶系和布拉伐格子 晶系 轴和角度 布拉伐格子
斜方
长方
正方
六角
a≠b γ ≠90℃ a≠b γ = 90℃ a=b γ = 90℃ a=b γ=120℃
绪 论:《固体物理》的研究对象
一个超级大原子
T (0K附近)玻色-爱因斯坦凝聚态(BEC)
物 质 的 状 态
固态(晶体和非晶体) 液态(液晶体和非晶液体) 气态 (百万K) 等离子态:太阳(99%) 凝聚态物理
绪 论:《固体物理》的研究内容
晶体和非晶体的结构
固体理论: 电子,原子(离子)运动规律
固体宏观性质
固体材料的性质(半导体,金属,超导,绝缘体) 新型人工材料微观结构和宏观性质
高等固体物理-第三章

一维晶格的振动
晶格振动谱的推导
向下的箭头代表原子沿X轴向左振动 向上的箭头代表原子沿X轴向右振动 格波方程 格波波长
一 维 单 原 子 晶 格
xn Aei ( qnat )
格波波矢 格波相速度
2
2 1 cos qa m
2
qa sin m 2
这种 ω与q的关系称为一维单原子晶格(或布喇菲格子)中格 波的色散关系,或称振动频谱,注意ω为正。
School of Materials Science and Engineering / WHUT
晶格振动谱的推导
设由相同原子组成的一维无限 长晶格,如图示: 原子质量: m 平衡原子间距(晶格常数):a 离开平衡位臵距离:xi 设平衡时,两个原子间相互作用势能为U(a),令相对位移量 δ=xn-xn+1,则产生相对位移后,相互作用势能变成U(a+δ),则将 U(a+δ)在平衡位臵附近用Tailor级数展开,得到:
School of Materials Science and Engineering / WHUT
一维晶格的振动
晶格振动谱的推导
则第n个原子的运动方程可写成: F ma m d xn x x 2 x n 1 n 1 n dt 2 mxn xn1 xn1 2xn 即:
一 维 单 原 子 晶 格
可见在这种条件下第n’个原子与第n个原子具有相同的位相。进 而可看出,晶格中各个原子的振动存在固定的位相关系(原子振动相 互作用,相互联系)。这时可认为晶格中存在着角频率为ω的平面波,
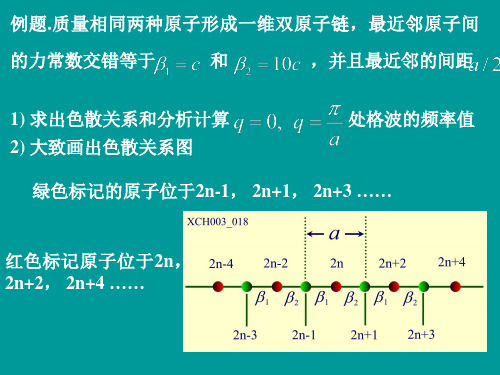
高等固体物理(基泰尔)例题
U G1 G0 E E1(0) U G1 G2 U G1 G3 0 (0) U G2 G0 U G2 G1 E E2 U G2 G3 U G3 G0 U G3 G1 U G3 G2 E E3(0)
O O nmax (max ) 0.222
E
O min
3.94 10 eV
2
n (
O min
O min
) 0.278
声学波频率的声子数目
A Emax 1.97 102 eV
A A nmax (max ) 0.876
二维正方格子
单原子晶体 德拜近似(连续弹性介质声学波近似): 二维:两支声学格波(一纵、一横) 两种极化方式 色散关系:线性 =vk 总模式数:2N 对于倒空间,k值密度:(L/2)2 对每种偏振模式:N=(L/2)2(k2) 模式密度:D()=dN/d 德拜温度: 晶格比热:
势能的平均值
势能的平均值
令
2 a2 b 函数的第n个傅里叶系数
第一个带隙宽度
E g1 2V1
2 a 3 m 2 3 m 2 2 第二个带隙宽度
8b 2
E g 2 2V2
a2 2 2 m m 16 2
2
b2
例题 用紧束缚近似求出面心
立方晶格和体心立方晶格s态 原子能级相对应的能带 函数 面心立方晶格 —— s态原子能级相对应的能带函数
—— s原子态波函数具有球对称性
—— 任选取一个格点为原点 —— 最近邻格点有12个
O
12个最邻近格点的位置
O
—— 类似的表示共有12项
—— 归并化简后得到面心立方s态原子能级相对应的能带
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高等固体物理学
固体物理作为凝聚态物理学中最大的分支,以固体特别是原子排列具有周期性结构的晶体为对象,基本任务是从微观上解释固体物质的宏观物理性质、构成物质的各种粒子的运动形态及其相互关系,是物理学中内容极丰富、应用极广泛的分支学科。
最近几十年来,由于新的实验条件和技术以前所未有的速度发展和进步,新材料不断涌现,因此不断开拓出固体物理新的研究领域。
同时,固体物理学的成就和实验手段对电子技术、计算技术以至整个信息产业、化学物理、催化学科、生命科学、地学等的影响日益增长,正在形成许多新的交叉学科。
对于经济和社会乃至人类日常生活具有革命性的影响。
本书对固体物理前沿的许多重要课题给出了简明的介绍,以清晰的教学方式提供了该领域已经得到很好确立的基础的背景材料。
把导论性的介绍与不断更新的高等论题成功地整合在一起,相关领域的研究生与高水平的研究人员将会从中受益并引起广泛的兴趣。
而对于希望对当代固体物理巨大的挑战得到一些概览的其他领域的学者也很有价值。
全书内容共分16章:1.导言;2.无相互作用电子气;
3.BornOppenheimer近似;
4.二次量子化;
5.HatreeFock近似;
6.相互作用电子气;
7.金属中的局域磁矩;
8.局域磁矩的淬火:近藤问题;
9.屏蔽与等离子体激元;10.玻色化;11.电子-晶格相互作用;12.金属中的超导电性;13.无序:定域与例外;14.量子相变;15.量子Hall效应及其它拓扑态;16.强耦合电子:莫特性(Mottness)。
本书把传统主题与现代进展有机地结合在一起的写作风格是其它书籍很少见到的。
它的内容清新、广泛,行文清晰,且容易理解,是高等固体物理学的一部很有价值的参考书。
