模式分解
模式分解例题

模式分解例题设有关系模式R(U, F),其中U={A ,B, C, D, E } , F = {AB C,B D, D E, C B },试问R最高为第几范式,并解释原因?如果R不是3NF或BCNF,要求将其分解为3NF和BCNF关系R中的函数依赖如下图表示R :A,B C ;B D ;D E ;C B第一范式规定关系的每一个分量必须是一个不可分的数据项。
可以看出,该关系满足第一范式。
如果关系模式R满足第一范式,且它的任何一个非主属性都完全函数依赖于任一个候选码,则R满足第二范式(简记为2NF)。
所以不是第二范式分解成第二范式R1 :A,B C ;C BR2:B D ;D E ;如果关系模式R满足2NF,并且它的任何一个非主属性都不传递依赖于任何候选码,则称R是第三范式(3NF),记作R 3NF。
分解成第三范式R1 :A,B C ;C BR21:B DR22:D E? 如果关系模式R是1NF,且每个属性都不传递依赖于R的候选码,那么称R是BCNF的模式。
R1 :A ,B C;C BR21:B DR22:D ER1中属性B传递依赖于R的候选码AB,故R1不是BCNF范式关系模式R 1NF,若X Y,且Y X时,X必含有候选码,则R BCNF。
R1中C B,且B C,但B不含有任何候选码,故R1不是BCNF范式分解成BCNF范式R11 :A,BR12 :C BR21:B DR22:D E候选码是什么?能够唯一标识一个元组的某一属性或属性组。
候选码:(A,B)和(A,C)假设有一个名为参加的关系,该关系有属性:职工(职工名)、工程(工程名)、时数(花费在工程上的小时数)和工资(职工的工资);一个参加记录描述一个职工花费在一个工程上的总时数和他的工资;另外,一个职工可以参加多个工程,多个职工可以参加同一个工程(用A、B、C、D 分别代表属性职工、工程、时数和工资)。
请回答如下各问题:1)确定这个关系的关键字;AB2)找出这个关系中的所有函数依赖;AB->C , A->D3)指出这个关系上的哪些函数依赖会带来操作异常现象;D对关键字AB的部分函数依赖可能会带来如下问题:数据冗余:一个职工参加多个工程,则职工的工资值会重复;更新异常:当改变职工的工资时,可能会只修改了一部分,从而造成数据不一致;插入异常:当一个职工尚未承担工程,但要插入职工信息(如工资)则不允许(因为没有完整的关键字);删除异常:当某个工程结束,删除工程信息时,可能会将职工信息(如工资)一同删除(如果职工只参加了一项工程)。
《关系模式分解》课件

索引优化
通过合理的关系模式分解,可以 为查询语句创建更有效的索引, 提高查询效率。
查询优化
分解后的关系模式可以简化查询 逻辑,减少查询复杂度,提高查 询效率。
缓存策略应用
利用数据库的缓存策略,可以减 少对物理存储的访问次数,提高 数据查询效率。
05
CATALOGUE
关系模式分解的挑战与未来发展
数据冗余问题
数据完整性维护
主键和外键约束
01
关系模式分解后,可以通过主键和外键约束来维护数据的完整
性,确保数据的准确性和一致性。
数据完整性检查
02
通过定期的数据完整性检查,可以及时发现并修复数据异常,
保证数据的可靠性。
事务处理能力
03
关系模式分解后,可以利用数据库的事务处理能力,确保数据
的完整性和一致性。
数据查询效率提升
案例二
总结词
数据安全与隐私保护
详细描述
某银行客户信息管理系统涉及到客户、账户、交易等多个实体的关系,这些关系中包含敏感信息。通 过关系模式分解,可以将敏感信息隐藏在虚拟属性中,降低数据泄露的风险,提高数据的安全性和隐 私保护。
案例三:某社交网络的关系模式分解
总结词
网络结构分析
详细描述
社交网络中存在着各种复杂的关系,如用户之间的关注关系、互动关系等。通过关系模 式分解,可以深入分析这些关系的结构特征,挖掘网络中的核心节点和社区结构,为社
关系模式分解
目录
• 关系模式分解简介 • 关系模式分解的基本概念 • 关系模式分解的方法 • 关系模式分解的应用 • 关系模式分解的挑战与未来发展 • 关系模式分解的案例分析
01
CATALOGUE
模式分解——无损连接分解
模式分解 ——无损连接分解
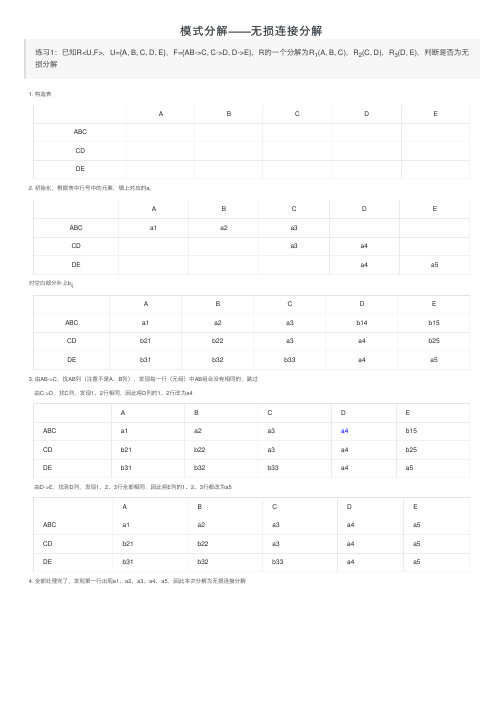
练习1:已知R<U,F>,U={A, B, C, D, E},F={AB->C, C->D, D->E},R的一个分解为R1(A, B, C),R2(C, D),R3(D, E),判断是否为无 损分解
1. 构造表
D
E
D
E
a4
a4Βιβλιοθήκη a5DEb14
b15
a4
b25
a4
a5
D a4 a4 a4
D a4 a4 a4
E b15 b25 a5
E a5 a5 a5
A
B
C
ABC
CD
DE
2. 初始化,根据表中行号中的元素,填上对应的ai
A
B
C
ABC
a1
a2
a3
CD
a3
DE
对空白部分补上bij
A
B
C
ABC
a1
a2
a3
CD
b21
b22
a3
DE
b31
b32
b33
3. 由AB->C,找AB列(注意不是A、B列),发现每一行(元组)中AB组合没有相同的,跳过 由C->D,找C列,发现1、2行相同,因此将D列的1、2行改为a4
A
B
C
ABC
a1
a2
a3
CD
b21
b22
a3
DE
b31
b32
b33
由D->E,找到D列,发现1、2、3行全部相同,因此将E列的1、2、3行都改为a5
A
模式分解

2.保持FD (函数依赖)的分解定义1:设F 是属性集U 上的FD 集,Z 是U 的子集,F 在Z 上的投影用πZ (F)表示,定义为πZ (F)={X →Y|X →Y ∈F +,且XY ⊆Z}定义2. 设},...{1K R R =ρ 是R 的一个分解,F 是R 上的FD 集,如果有)(1F R i ki π=Y ╞ F ,那么称分解ρ保持函数依赖集F 。
根据定义1,测试一个分解是否保持FD ,比较可行的方法是逐步验证F 中的每个FD 是否被)(1F R i ki π=Y 逻辑蕴涵。
如果F 的投影不蕴涵F ,而我们又用},...{1K R R =ρ表达R ,很可能会找到一个数据库实例σ 满足投影后的依赖,但不满足F 。
对σ的更新也有可能使r 违反FD 。
案例1:R (T#,TITLE ,SALARY )。
如果规定每个教师只有一个职称,并且每个职称只有 一个工资数目,那么R 上的FD 有T#→TITLE 和TITLE →SALARY 。
如果R 分解成ρ={R 1,R 2},其中R 1={T#,TITLE},R 2={T#,SALARY }。
则该分解具有无损连接性,但未保持函数依赖,丢失了依赖TITLE →SALARY 。
习题1:设关系模式R (ABC ),ρ={AB ,AC}是R 的一个分解。
试分析分别在F 1={A →B};F 2={A →C ,B →C},F 3={B →A},F 4={C→B,B→A}情况下, 是否具有无损分解和保持FD的分解特性。
算法1:分解成2NF模式集的算法设关系模式R(U),主码是W,R上还存在FD X→Z,并且Z是非主属性和X⊂W,那么W→Z就是非主属性对码的部分依赖。
此时,应把R分解成两个关系模式:R1(XZ),主码是X;R2(Y),其中Y=U-Z,主码仍为W,外码是X(参照R1)利用外码和主码的连接可以从R1和R2重新得到R。
如果R1和R2还不是2NF,则重复上述过程,一直到数据库模式中的每个关系模式都是2NF为止。
模式的分解

}
2018/10/5
11
判断无损连接的算法
算法6.2 判断一个分解的无损连接性 {R1 U1, F1 , R2 U2 , F2 ,..., Rk Uk , Fk是 }R<U,F〉的一 个分解,U={A1,A2,…,An},F={FD1,FD2,…, FDm},这里我们设F是一个极小依赖集,记FDi为 Xi→Ali。 (1)建立一张n列k行的表。一列对应一个属 性,一行对应一个分解后的模式;在i行j列中的空白 处,若属性Aj属于Ui,则填上aj,否则填上bij。
2018/10/5
8
6.4.2.1 分解的“无损连接性”
我们先来定义几个符号: 分解: {R1 U1, F1 , R2 U2 , F2 ,..., Rk Uk , Fk } 其中r是R<U,F>的一个关系。 再定义: m = ( r ) Ri 也就是说 是r在各个模式分解上的投 m 影的连接。
2018/10/5 3
本小节要讨论的内容
• “无损连接性”和“保持函数依赖”的含 义; • 对于这三种角度的分解可以达到的分离程 度,即可以达到第几范式; • 对于这几种分离的分解算法;
下面用一个实际分解的例子来引出本小 节的内容。
2018/10/5 4
一个分解实例
例4:一个关系模式R<U,F>,其中U={Sno,Sdept, Mn},F={Sno→Sdept,Sdept →Mn}。 如果我们把它分解成:
我们从r1,r2和r3这三个关系中已经不能回 答“某个学生在哪个系学习”了,显然这样的分 解是失败的。这是由于失去了关原来的关系。 而我们把r1,r2和r3做自然连接(它们的笛卡 尔积)后,我们得到的是一个具有4*4*4=64行的 没有实际意义的关系表。不能恢复表5.3所示的 含义了。
6.4模式的分解

算法6.5:(分解法)转换为BCNF的 无损连接分解*
例:R(U,F),U={X,Y,Z},F={Y→Z,XZ→Y}, 在保持无 损连接的情况下分解为BCNF。 解答:R的侯选码为XY和XZ;R为3NF。
由于存在着Y→Z,而Y不是码,根据算法6.5将R 分解为R1{(Y,Z),(Y→Z)}
分析两种分解的依赖保持性?
分解1:只有AB,显然,分解1不具有依赖保持性 分解2:保留了所有函数依赖,具有依赖保持性
简单练习: 判定无损连接性和函数依赖性
设S-C-M(S学号,C班级,M班主任)
F={S学号C班级,C班级M班主任,S学号M班主任}
1 {S C (学号,班级),C M (班级,班主任)} 2 {S C (学号,班级),S M (学号,班主任)} 3 {S M (学号,班主任),C M (班级,班主任)}
求得F ' F {S D, I B, IS Q, B O}, 故可得R的保持函数依赖的 3NF分解 {SD, IB, ISQ, BO}, 另外,F '中L, N类属性为I , S , 且( IS ) ISDBOQ 包含所有属性 , 故IS为唯一的候选码。在 的基础上增加IS即为R的无损连接 且保持函数依赖的 3NF分解。
分别求解F 和( Fi ) , 若两者相等,则表示分 解
i 1 k
前后的函数依赖集是等 价的,即具有保持函数 依赖性
例子
R(A,B,C), F={AB, C B}
分解1={(A,B) {AB},
分解2={(A,B) {AB}),
(A,C) }
(B,C) {C B}}
关系模式分解

举例:
例 5.8 设 有 关 系 模 式 R(A,B,C) , 函 数 依 赖 集
F={A→B , C→B} , 分 解 ρ ={R1,R2} , 其 中 R1=AB , R2=BC 。检验分解 ρ 是否具有无损联 接性。 分解ρ不具有无损联接性
三、保持函数依赖集
1、定义
设有关系模式 R(U,F) , F 是 R 的函数依赖集, ρ ={R1,R2,…,Rk}是R上的一个分解。如果所有函 数依赖集πRi(F)(i=1,2,…,k)的并集逻辑蕴 含 F 中的每一个函数依赖,则称分解 ρ 具有依赖 保持性,也即分解ρ 保持依赖集F。即
A R1 R2 R3 R4 R5 a1 a1 a1 a1 a1 B b12 a2 a2 b42 b52 C b13 b13 a3 a3 a3 D a4 a4 a4 a4 a4 E b15 b25 a5 a5 a5
例 5.7 设R(ABCDE),F={A→C,B→C,C→D,DE→C,
CE→A},ρ={R1(AD),R2(AB),R3(BE),R4(CDE), R5(AE)},检验分解ρ是否具有无损联接性。 第三步:判断
2、算法5.2 判断一个分解的无损联接性 输入:关系模式R(A1,…,An),
函数依赖集F,
R的一个分解ρ =(R1,…,Rk)。
输出:ρ 是否为无损联接的判断。 方法:
2、算法5.2 判断一个分解的无损联接性(续1)
(1)构造一个k行n列表S,其中:
A1 R1 … Ri … Rk … Aj … An
例 5.7 设R(ABCDE),F={A→C,B→C,C→D,DE→C,
CE→A},ρ={R1(AD),R2(AB),R3(BE),R4(CDE), R5(AE)},检验分解ρ是否具有无损联接性。 第二步:修正②B→C
第13讲模式分解

第13讲模式分解第13讲的主题是模式分解。
在这一讲中,我将向你介绍什么是模式分解,以及如何使用模式分解来解决问题。
首先,让我们来了解一下什么是模式。
模式是一种可重复的结构或行为方式,可以在不同的问题或情境中重复使用。
模式可以是实际存在的实体或过程,也可以是思维模式或行为模式。
模式分解是一种分析问题的方法,通过将问题分解成更小的、更具体的子问题来解决问题。
这种方法可以使复杂的问题变得更加可管理,并帮助我们更好地理解问题的本质。
模式分解的过程通常包括以下几个步骤:1.确定大问题:首先,我们需要明确整个问题的大框架和目标。
这有助于我们保持对问题的整体认识,并指导我们进行模式分解的过程。
2.列举模式:接下来,我们需要在问题中识别出重复出现的模式。
这些模式可能是具体的步骤、观念、数字等等。
列举这些模式有助于我们识别问题中的重点,并为下一步的分解提供线索。
3.分解子问题:一旦我们明确了模式,我们就可以将整个问题切分成更小的、更具体的子问题。
这可以通过将具有共同模式的元素归为一组来实现。
每个子问题都可以独立地解决,并且通过组合子问题的解决方案,可以获得整个问题的解决方案。
4.解决子问题:然后,我们需要逐个解决子问题。
这可能需要使用之前学到的其中一种解决技术,例如算法、数学公式、模拟等。
在解决子问题的过程中,我们可以进一步细化问题,并将其分解成更小的更具体的部分。
5.合并子问题:最后,我们需要将解决子问题的结果合并起来,以获得整个问题的解决方案。
这可以通过将子问题的解决方案进行组合操作来实现。
在合并子问题时,我们还需要确保解决方案的一致性和有效性。
通过模式分解,我们可以将复杂的问题分解成更小的、更容易处理的子问题,从而简化问题的解决过程,并提高解决问题的效率。
此外,模式分解还可以帮助我们深入了解问题的本质,识别出隐藏的模式和规律。
总结来说,模式分解是一种分析和解决问题的方法,通过将问题分解成更小的、更具体的子问题,并逐个解决这些子问题,最终得到整个问题的解决方案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
判断无损分解的方法。
原来数据库所有信息为前提来实现。其根本目标是节省存储空间, 避免数据不一致性,提高对关系的操作效率,同时满足应用需求。 实 际上,并不一定要求全部模式都达到BCNF不可。有时故意保留 部分 冗余可能更方便数据查询。尤其对于那些更新频度不高,查询 频度极 高的数据库系统更是如此。
小结
模式分解的定义。 无 损分解的定义。
i=l
•保持函数依赖分解还牵涉到其它相关的基本知识,在这里我们不作为 重 点来讲解。
6・6模式分解
回算法6.3判定分解的无损连接性
输入
关系模式R<U, F>的的一个分解p = (R1<U1, F1>, R2<U2, F2>,…,Rk<Uk, Fk>}
6・6模式分解
输出
•P是否为无损连接分解的判定
设关系模式RvU, F> ,如果把它分解为两 个 或多个子模式R1和R2,相应一个R关 系中 的数据就要被分解成R1、R2两个或 多个子 表。假如将这些子表自然连接, 即进行 R18R2操作,得到的结果与原来 关系中的 数据一致,信息并没有丢失,则 称该分解 具有无损连接性,否则如果R示 18R2,则 称该分解不具有无损连接性。
•重复如下过程,直到表不发生变化或一行成为a〔a2... ano
6・6模式分解
例:设关系模式R (ABCD), R分解成p=(AB, BC, CD}。如果R上成立的函 数依赖
集F1={B—A, C一D},那么p相对于F1是否为无损分解?如果R上成立的 函数
依赖集F2={A—B, C-D}呢? 解:利用算法6.3进行判断,在依赖集F1 上有: 1,利用算法6.3第一步,求出初始表格如图:
6・6模式分解
定义
•如果我们对折分后的子表进行复原工作,原表中所存在的函数依赖关 系 仍然存在,我们就说模式分解是保持了函数依赖的。
•设p={R1<U1, F1>, R2<U2, F2>z ... , Rn<Un, Fn> }是关系模式 RvU, F>的一个分解,p是保持函数依赖的分解,如果:
kstem
数据库系统概论
Introduction to Database Systems
主讲人:王岩 河南理工大学
知
第六章关系的规范化理论
识
点
\1 )模式设计中存的问题
2)函数依赖
❸第一范式和第二范式
(4 )第三范式
(5 ) BC范式
6)模式分解
6・6模式分解
定义
设有关系模式R (U)和R1 (U1) , R2 (U2) , Rk (Uk), 其中U={A1, A2, ......, An}, Ui包含于U (i=1, 2, k)且U =U1 o 令p={R1 (U1) , R2 (U2) , R (Uk) ), 则称p为R (U)的一个分解,也称为数据库模式,有时也称为模式 集。用p代替R (U)的过程称为关系模式的分解。
解:利用算法6.3进行判断,在依赖集F2上有: 1,利用算法6.3第一步,求出初始表格如图:
6・6模式分解
解:利用算法6.3进行判断
2,根据C一D,可把b24改成a4。据ATB,不能修改表格。此时表格没有一行 全 a行,因此相对于F2,R分解成p是损失分解。示意图如表所示。
6・6模式分解
注意:
一个关系模式分解可以得到不同关系模式集合,也就是说分解 方法不是唯一的。最小冗余的要求必须以分解后的数据库能够表达
从定义中可以看出模式分解的结果就是把表折分为多个表的,相应的原来 存 储在一张二维表中的数据就要分散存储到多张二维表中去。
6・6模式分解
\=\无损连接分解
般定义
形式化定义
对折分结果最基本的要求肯定是不能丢 失原来的信息。也就是说,我们所拆分 的这些子表应该能通过自然连接所得到 的结果与原来的表中的数据一致,如果 能达到这个要求,我们称该分解是无损 连接性的。
6・6模式分解
解:利用算法6.3进行判断 2,对函数依赖集F1,因为BTA,可以把改成al,据CTD,可把b24改成 a4o些时第 二行已是全a行,因此相对F1, R分解成p是无损分解。示意图如 表所示。
6・6模式分解
例:设关系模式R (ABCD), R分解成p={AB, BC, CD)。如果R上成立的函数依赖 集 F1={BTA, CTD},那么p相对于F1是否为无损分解?如果R上成立的函数依赖 集 F2={ATB, CTD}呢?
