静定刚架受力分析
静定平面刚架的内力分析- 内力图

静定平面刚架的内力分析 • 内力图
1.1 刚架结构的特征和基本类型
1. 刚架结构的特征
刚架是用刚结点将若干直杆联结而成的结构。当刚架的轴线和外力都在同一 平面时,此种钢架称为平面刚架。由静力平衡条件可以求出全部约束反力和内力 的平面刚架称为静定平面刚架。
刚架在构造方面具有杆件少、内部空间大、便于使用等特点;在受力方面, 由于刚结点能承受和传递弯矩,从而使结构中弯矩的分布较均匀,峰值较小,节 约材料。因此,刚架结构在工程中是最为常见的一种结构。
2. 静定平面刚架的基本类型 静定平面刚架的基本类型有三种:悬臂刚架、简支刚架和三铰刚架,分别如 图9-4 a 、b 、c 所示。
图9-4
1.2 静定平面刚架的内力计算及内力图绘制
静定平面刚架横截面上的内力一般有轴力 FN 、剪力 FQ 和弯矩 M 等三个内力, 其内力的计算方法与静定梁基本相同。通常将刚架拆成单个杆件,求出各杆的杆 端内力,然后利用杆端内力分别作出各杆件的内力图,再将各杆件的内力图组合 在一起,即得刚架的内力图。
计算杆端内力时,杆端内力的表示方法是在内力符号后面加两个下角标。例 如,对杆 AB 的杆端内力可表示为:MAB 表示杆 AB 在 A 端的弯矩,MBA 表示杆AB 在 B 端的弯矩;FQAB 表示杆 AB 在 A 端的剪力,FQBA 表示杆 AB 在 B 端的剪力。
在作刚架的内力图时,通常将弯矩图画在杆件弯曲时受拉的一侧,而不必标 注正负号;在作剪力图和轴力图时,剪力和轴力可画在杆件的任一侧,但必须标明 正负号。下面举例说明。
图9-6
② 求各杆的杆端弯矩,作 M 图。
杆CE :
M CE
22
4
1 2
8
42
24
结构力学3静定刚架受力分析

C
∑F = 0,
x
XB + XC = 0, XC = −P(↓)
XC
YC
B
XB
YB
3)取整体为隔离体 取整体为隔离体 ∑Fy = 0,YA +YB = 0,YA = −YB = −P(↓) l ∑ M A = 0, M A + P × 2 − YB × l = 0, 1 M A = Pl (顺时针转 ) 2
Pl
Pl
P
l
l
l
练习: 练习 试找出图示结构弯矩图的错误
练习: 练习 试找出图示结构弯矩图的错误
本章小结
一. 刚架的受力特点 二. 刚架的支座反力计算 三. 刚架指定截面内力计算 四.刚架弯矩图的绘制 五.计算结果的校核
作业
3-3 (a) 3-7(a) 3-8(c)
P
P
Pl
P
P
P
P
Pl
P
P
连接两个杆端的刚结点, 连接两个杆端的刚结点 §3-3 静定刚架受力分析 ,若 结点上无外力偶作用, 结点上无外力偶作用,则两 三. 刚架指定截面内力计算 个杆端的弯矩值相等, 个杆端的弯矩值相等,方向 与梁的指定截面内力计算方法相同. 与梁的指定截面内力计算方法相同. 相反. 相反.
第三章 静定结构受力分析
§3-3 静定刚架受力分析
§3-3 静定刚架受力分析
一. 刚架的受力特点
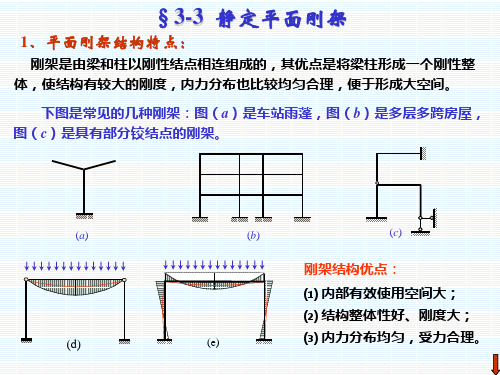
刚架是由梁柱组成的含有刚结点的杆件结构
1 2 ql l 8
梁
桁架
1 2 ql 8
弯矩分布均匀 可利用空间大
刚架
§3-3 静定刚架受力分析
二. 刚架的支座反力计算
静定刚架的分类: 静定刚架的分类 三铰刚架 (三铰结构 三铰结构) 三铰结构
结构力学 第3章静 定梁、平面刚架受力分析

q 与 q’间的转换关系:
qdx qds q q
cos
第3章
[例题] 试绘制图示斜梁内力图。
q
B
C
A
α
D VB
HA
l/3 l/3
l/3
VA
(1)求支座反力:
解:
X 0 MB 0 MA 0
HA 0
VA
ql 6
()
VB
ql 6
()
校核:
Y
qj 6
qj 6
ql 3
0
第3章
(2)AC段受力图:
(3)AD段受力图:
HAcosα HAsinα
HA VAsinα
VA VAcosα
MC
C
NC
α QC
HAcosα
dx
d2M dx2
q(x)
(1)在无荷区段q(x)=0,剪力图为水平直线,弯矩图为斜直线。
(2)在q(x)=常量段,剪力图为斜直线,弯矩图为二次抛物线。其凹下去的曲 线象锅底一样兜住q(x)的箭头。
(3)集中力作用点两侧,剪力值有突变、弯矩图形成尖点;集中力偶作用点两 侧,弯矩值突变、剪力值无变化。
解:
10KN/m A HA=0
4m VA=26.25kN
30KN.m
20KN
C
D
B
E
2m
2m
32.5 2.5
3m VB=33.75KN 60
(1)计算支座反力
静定梁和刚架内力分析

(0<x<l ) (0≤x<l)
M
(-)
(c)
x
2.作剪力图和弯矩图:
由剪力方程可知,当 0 <x <l,时(即 AB 段上),剪力为 常数,因此剪力图为一条水平的直线;由弯矩方程可知,AB 梁段上沿着轴线方向弯矩呈线性变化,因此,弯矩图为一条斜 直线,只需求出两个端截面上
F A FQ x m m l
在列平衡方程求解内力时,需事先确定截面内力的方向, 而此时截面内力为未知力,因此,一般假定截面内力沿其正向 作用,则计算得到的正负号就是该截面内力的正负号。 另外,在利用截面法求解前,通常先确定支座反力,因支 座反力并无正负规定,在求支反力前可任意假设正方向。
若结果为正,则表示支反力实际方向与假设方向相同;
上所有外力对该截面形心的力矩的代数和。
其中外力对横截面形心之矩正负号选取规律为: (1)力——不论横截面左侧还是右侧,只要向上就取正,
反之取负;
(2)力偶——横截面左侧顺时针或右侧逆时针取正,反之 取负。 利用上述结论,可以不画分离体的受力图、不列平衡方 程,直接得出横截面的剪力和弯矩。这种方法称为直接法。 直接法将在以后求指定截面内力中被广泛使用。
2
求梁指定截面上的内力的方法: 剪力:梁任一横截面上的剪力在数值上等于该截面一侧梁段 上所有外力在平行于截面方向投影的代数和。 其中外力正负号选取规律为: 横截面左侧梁段上向上的外力取正,横截面右侧梁段上
向下的外力取正;反之取负。
简记为左上右下取正,反之取负。
弯矩:梁任一横截面上的弯矩在数值上等于该截面一侧梁段
若外力或外力偶矩使所考虑的梁段产生向下凸的变形(即 上部受压,下部受拉)时,等式右方取正号,反之,取负号。 此规律可简化记为“下凸弯矩正”或“左顺,右逆弯矩 正” ,相反为负。
《结构力学》_龙驭球_第3章_静定结构的受力分析(2)
一、求支座反力
40 kN
在支座反力的计算过程中,应尽可能建立 独立方程。
B
D
C
20 kN/m
4m
MA 0 FY 0
FDY 4 40 2 (20 4) 2 0 FDY 60kN () FAY 40 60 0 FAY 20kN ()
FX 0 FAX 80kN ()
二、绘制内力图
⑴ 分段:根据荷载不连续点、结点;
解,本题剪力很容易用投影方程求得。
4kN/m
1kN
C
MDE D
E
8
14kN
4m
1kN B 4m
2kN
28 24
4
4D
8
E
F
A
B
M 图(kN·m)
14
D
E
2
2
16
1
F
A
B
FQ 图(kN)
③ 作FN 图 各杆轴力可以用投影方程求
解。也可根据剪力图, 取各结点 为隔离体,用投影方程求轴力。
④ 校核
16
14
40
载和B端外力偶作用的简支梁(图C)。
画M图时,将 B 端弯矩竖标画在受拉 80 A
侧,连以虚直线,再叠加上横向荷载产生
20
的简支梁的弯矩图,如图(d)示。
(b)
A
A
(c)
(d)
B 160
D
160
120
20 60
120
20
A M图 (kN·m)
80 F Q 图(kN)
F N 图(kN)
练习3-3.1:试计算图示简支刚架的支座反力,并绘制M、F Q 和 F N 图。
Fx 0, FBx 2 11kN()
结构力学3静定结构的受力分析-刚架

1 结构力学多媒体课件1、刚架由梁和柱组成的结构,其结点全部或部分是刚结点。
2、刚架的形式2)简支刚架1)悬臂刚架2、刚架的形式3)三铰刚架4)主从刚架3、刚架的特点1)杆数少,净空大,便于使用3、刚架的特点2)刚结点的特点①变形:刚结点处的各杆端不能发生相对移动和相对转动,因而受力变形后,各杆杆端转动了同一角度,即各杆之间的夹角保持不变。
②受力:刚结点可承受和传递弯矩保持角度不变3、刚架的特点3)横梁和竖柱连成整体,使整体刚度增大,弯矩的峰值减少二、刚架中各杆的杆端内力1、支座反力的计算⑴求反力时要先根据支座的性质正确定出反力未知量个数,不能多、不能少。
⑵假定反力方向,由平衡方程确定其数值。
⑶应尽量利用一个平衡方程求一个未知力。
⑷求出反力后要有没有用过的平衡方程校核。
l /2l /2l /2l /2CBAPF AY =0.5PF BY =0.5PF AX=0.75P F BX =0.25P2m 2m 4mCBA4m2kN/mGFEDF AX =1KNF CX =1KNF CY =3KNF BY =7KN2、杆端内力的计算⑴方法:截面法⑵内力符号结点处有不同的杆端截面。
各截面上的内力用该杆两端字母作为下标来表示,并把该端字母列在前面。
——AB杆A端的轴力。
FN AB——AB杆A端的剪力。
FQ AB——AB杆A端的弯矩。
MAB2、杆端内力的计算⑶内力的正负规定轴力FN:以拉力为正,压力为负。
剪力FQ:以绕隔离体顺时针转为正,反之为负。
弯矩M:不规定正负,但弯矩图画在受拉侧。
F N FNF Q F QM AB M BAF NF NF QF Q MBAM AB 竖杆剪力图和轴力图可画在任一侧,但必须标出正负;弯矩图画在受拉一侧,可不标正负。
2、杆端内力的计算 ⑷正确选取脱离体⑸注意结点平衡∑F X =0 ∑F Y =0 ∑M D =0一般先求出支座反力及铰结点处的内约束力,然后将刚架拆成杆件,逐杆绘制其内力图,将各杆的内力图合在一起就是刚架的内力图。
静定结构的内力—静定平面刚架(建筑力学)

对于比较复杂的情况,可取结点为隔离体,根据已知FS ,利用投影方程,求杆件轴力值。
【说明2】绘图规定:
1、M图约定绘在刚架的杆件受拉一侧,不标注正负号; 2、FS图和N图可绘在杆件的任一侧,但必须标注正负 号,一般杆左或杆上为正,杆右
【例1】试求作图示刚架的内力图。
FP
A
B
FP
FP
4
C
l
l
l/2
l/2 D
FP 4
FP
A
B
FPl
A
4
l/2
FP
FP
4
C
l/2 D
l
l
FP
4
B
C
D
FPl
4
M图
解: (1) 求支反力 (2)求作M图
MCB(求)
FPl
C
4
FPl
B
4
MBC(求)
A
B
FP FP/4
C FP/4
D
FS图
A
B
FP/4
FP
C
D
或杆下为负;其符号正负规定与梁相同。
【说明3】关于简单刚结点的概念,节点平衡
只有两杆相交组成的刚结点,称为简单刚结点。当无外力偶作用时,汇交于该处两杆的 杆端弯矩坐标 应绘在结点的同一侧(同在内侧或同在外侧),且数值相等。作M图时,可 充分利用这一特性。
【说明4】脱离体法是求内力的最基本方法,不要忘记。
绘制刚架内力图的要点总结如下:
(4)绘制杆件的轴力图,在只有横向垂直于杆件轴线荷载的情况下,只需 求出杆件一端的轴力,轴力图即可画出。 (5)必须进行内力图的校核。通常取刚架的一部分或一结点为分离体,按 已绘制的内力图画出分离体的受力图,验算该受力图上各内力是否满足 平衡方程
结构力学 4静定结构受力分析-刚架

P
Ph Ph a
P
h Ph a
集中力偶作用处无变化发生突变两直线平行集中力偶作用点弯矩无定义荷载不符注意这个铰该处支座反力沿着杆件轴线方向不产生弯矩铰上无弯矩集中力偶处弯矩有突变弯矩图正误判断作用在结点上的各杆端弯矩及结点集中力偶不满足平衡条件
静定结构受力分析
几何特性: 无多余联系的几何不变体系 几何特性: 静力特征: 仅由静力平衡条件可求全部反力、内力。 静力特征: 求解一般原则: 求解一般原则:从几何组成入手,按组成的相反 顺序进行逐步分析即可 本章内容: 静定梁;静定刚架 静定刚架; 三铰拱;静定 本章内容: 静定刚架 桁架;静定组合结构;静定结构总论 学习中应注意的问题:多思考,勤动手。本章是 学习中应注意的问题: 后面学习的基础,十分重要, 要熟练掌握!
几点说明 刚架内力仍然可以利用q、Q、M微分关系。 微分关系。 内力符号规定: 内力符号规定: N —— 拉力为正 Q —— 使杆段顺时针转动为正 M —— 绘在受拉一边 内力记号: 内力记号: NAB ——AB杆A端的轴力。 端的轴力。 杆 端的轴力 QAB——AB杆A端的剪力。 端的剪力。 杆 端的剪力 MAB ——AB杆A端的弯矩。 端的弯矩。 杆 端的弯矩
Q=0区段M图 平行于轴线
Q=0处
M
集中力作用 力无
集中力偶作用点 无
判断下列结构弯矩图形状是否正确,错的请改正。 判断下列结构弯矩图形状是否正确,错的请改正。
P D ↓↓↓↓↓↓↓↓ P D q ↓↓↓↓↓↓↓↓
×
B
C
×
E (a)
弯矩 图与 荷载 不符
B
C
q
A
A (b)
E
↓↓↓↓↓↓↓↓↓↓↓
×
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
16
§2-2 静定连接刚两架个受杆力端的分刚析结点,若
三. 刚架指定截面结个内点杆力上端计无的算外弯力矩偶值作相用等,,则 方两 向
与梁的指定截面相内反力. 计算方法相同.
例1: 求图示刚架1,2截面的弯矩
M1
M
C1 2 l
2
M2
P
A
XA
l
2
YA
l
2
B
l
XB
2
YB
M
简支刚架
单体刚架 (联合结构)
悬臂刚架
复合刚架
(主从结构)
3
1.单体刚架(联合结构)的支座反力(约束力)计算
方法:切断两个刚片之间的约束,取一个刚片为隔离体,假定 约束力的方向,由隔离体的平衡建立三个平衡方程.
例1: 求图示刚架的支座反力
C
B
C
B
l
2
YB
P
lP
A
l
2
A X A YA
解:
Fx 0, X A P 0, X A P()
MA
0, P
l 2
YB
l
0,YB
P 2
()
Fy
0,YA
YB
0,YA
YB
P 2
()
4
例2: 求图示刚架的支座反力
q
ql2 解:
ql
Fx 0, X A ql 0, X A ql()
l
A
Fy 0,YA ql 0,YA ql()
XA
l 2
MA YA
l 2
M A 0, M A ql l ql2 0,
P/4
P/4
解:
M 2 Pl / 4(右侧受拉)
YB P / 2() YA P / 2() X B P / 4() X A P / 4()
M1 Pl / 4(上侧受拉)
M1 M 2 (外侧受拉)
17
P
P
Pl
P
P
P
P
P P
P
P
Pl
P
13
习题: 求图示体系约束力.
A
M BM
M
M /l
M /l
l
C
l
M /l D M /l
M /l M /l
14
习题: 求图示体系约束力.
l
l
M
l
l
l
M /l M /l
M
0
15
§2-2 静定刚架受力分析
一. 刚架的受力特点 二. 刚架的支座反力计算 三. 刚架指定截面内力计算
Fy 0, NCD 6P()
Fx 0, X A 0
Fy 0,YA YB P 0,YA 2P()
11
3.复合刚架(主从结构)的支座反力(约若束附力属)计部算分上无
例1: 求图示刚架的支座反力
l/2
D
方分反,.法计:算外约先顺算力束序附力,附与属是属几部否部何分为组,分后成零上算顺?基的序本相部
Fy M
D0,0N, NDCBCP1212PP(() )
Fx 0,
N DA
2
()
7
2.三铰刚架(三铰结构)的支座反力(约束力)计算
方法:取两次隔离体,每个隔离体包含一或两个刚片,建立六
个平衡方程求解--双截面法.
例1: 求图示刚架的支座反力
解:1)取整体为隔离体
P
XA YA
XC
C
A
B
l
l
l 2
l 2
MA Fy
0, P 0,YA
l 2
YB
l
0,
YB
YB 0,YA YB
P
2
() P () 2
X B Fx 0, X A P XB 0
2
2
YB
2)取右部分为隔离体
C YC
B
XB
l
P
MC
0,
XB
l
YB
2
0,
XB
P4
()
Fy Fx
0,YC YB 0, X B
0,YC YB XC 0, XC
第二章 静定结构受力分析
§2-2 静定刚架受力分析
1
§2-2 静定刚架受力分析
一. 刚架的受力特点
刚架是由梁柱组成的含有刚结点的杆件结构
梁
1 8
ql2
l
桁架
1 ql2 8
刚架
弯矩分布均匀 可利用空间大
2
§2-2 静定刚架受力分析
一. 刚架的受力特点 二. 刚架的支座反力计算
静定刚架的分类:
三铰刚架 (三铰结构)
l/4
P
l/4
A
B
XA
解:1)取附属部分
C
X D P()
l
l
YA
YB
YC
YC P / 4() YD P / 4()
A XA
YA
YD X D
D
XD
B
YD
YB
2)取基本部分
P C
YC
X A P() YA P() YB P / 4()
12
思考题: 图示体系支反力和约束力的计算途径是怎样的?
P
P
4
() 2 ()
YB
8
例2: 求图示刚架的支座反力和约束力
P MA
XC
解:1)取整体为隔离体
C
l
2
Fx 0, XB P()
A
l 2
YA
C
B
l
2
YB
l
2
2)取右部分为隔离体
X B
MC
0,
X
B
l
YB
l 2
0,YB
2P()
Fy 0,YC YB 0,YC YB 2P()
Fx 0, XB XC 0, XC P()
Fx 0, XC XB ql / 2()
Fy 0,YA YB 2ql 0,YA ql() 3)取AB为隔离体
2)取AC为隔离体
Fy 0, YC YA ql 0
Fx 0, XB X A ql / 2()
l MC 0, X A l ql 2 YB l 0, X A ql / 2()
10
例4: 求图示刚架的反力和约束力 P
B
l
XB YB
P
C
E
XB
B
CE
YB
N CD
N EF
XA
A
l
D
F
l
l
YA
3)取BCE为隔离体
解:1)取BCE为隔离体
Fx 0, XB 0
2)取整体为隔离体
MC 0, P l YB l NEF l 0,
NEF 4P()
MA 0, P3l YB l 0,YB 3P()
3)取整体为隔离体
YC
Fy 0,YA YB 0,YA YB P()
B
X B
M
A
0, M
A
P
l 2
YB
l
0,
YB
M
A
1 2
Pl(顺时针转)
9
例3: 求图示刚架的约束力 q
XA A
B XB
C
YA
2ql
YBAຫໍສະໝຸດ 2qlll
l B
XA A
C
XC
YC
解:1)取AB为隔离体
YA
l M A 0,2ql 2 YB l 0,YB ql()
MA
0, ql
l 2
XC
l
0,
XC
1 2
ql()
1 Fx 0, NAB XC 2 ql()
6
例5: 求图示刚架的反力和约束力
C P
XA
A
D
E
l
B
YA
l
l
YB
解: 1)取整体
Fx 0, X A P()
MA
0,YB
1 2
P()
Fy
0,YA
1 2
P()
N EC
E
N DC
N DA
B
D
YB
2)取DBE部分
M A 2ql2 (逆时针转)
C
B
XB
例3: 求图示刚架的支座反力
l
2
解:
Fx 0, X B P() l P
MB
Fy 0,YA 0
2
A
MB 0, MB pl / 2(顺时针转) YA
l
5
例4: 求图示刚架的约束力 q
C
A
ql
l
l
l
B
A
ql
ql
C
XC
YC
N AB
解:
Fy 0,YC 0
