材料力学-组合变形
合集下载
材料力学组合变形
第八章 组合变形
组合变形和叠加原理 拉伸或压缩与弯曲旳组合 扭转与弯曲旳组合
目录
§8-1 组合变形和叠加原理
一、组合变形旳概念
构件在荷载作用下发生两种或两种以上旳基本变形,则构件 旳变形称为组合变形.
l 基本变形 u 拉伸、压缩
u 剪切
u 扭转
u 弯曲
二、处理组合变形问题旳基本措施－叠加法
叠加原理旳成立要求:内力、应力、应变、变形等与外力之 间成线性关系.
M A(F) 0
F 42 kN
H 40 kN, V 12.8 kN
l 内力图 l 危险截面
C 截面
M C 12 kNm, N 40 kN
l 设计截面旳一般环节
u 先根据弯曲正应力选择工字钢型号； u 再按组合变形旳最大正应力校核强度，必要时选择大一号或 大二号旳工字钢； u 若剪力较大时，还需校核剪切强度。
按第四强度理论
Qy My T
r4
1 W
Mz Qz
M 2 0.75T 2 47.4 MPa [ ]
(3) 曲柄旳强度计算
l 危险截面 III-III截面
l 计算内力 u 取下半部分
Qx Qz
N R2 C1 13 kN Mx m H2 d /2
765 Nm
M z R2 (a b / 2) 660 Nm
横截面上任意一点 （ z, y） 处旳正应 力计算公式为
1.拉伸正应力
FN
A
2.弯曲正应力
Mz y
Iz
FN Mz y
A Iz
( z,y)
Mz
z
O
x
FN
y
3.危险截面旳拟定
作内力图
F1
轴力
组合变形和叠加原理 拉伸或压缩与弯曲旳组合 扭转与弯曲旳组合
目录
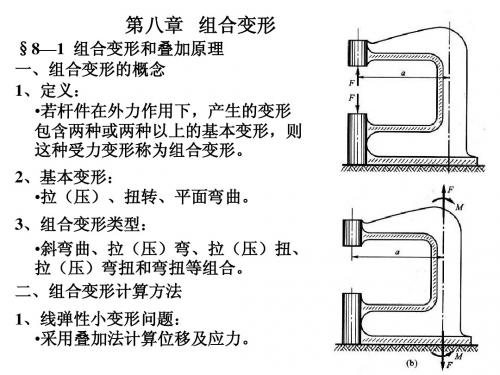
§8-1 组合变形和叠加原理
一、组合变形旳概念
构件在荷载作用下发生两种或两种以上旳基本变形,则构件 旳变形称为组合变形.
l 基本变形 u 拉伸、压缩
u 剪切
u 扭转
u 弯曲
二、处理组合变形问题旳基本措施－叠加法
叠加原理旳成立要求:内力、应力、应变、变形等与外力之 间成线性关系.
M A(F) 0
F 42 kN
H 40 kN, V 12.8 kN
l 内力图 l 危险截面
C 截面
M C 12 kNm, N 40 kN
l 设计截面旳一般环节
u 先根据弯曲正应力选择工字钢型号； u 再按组合变形旳最大正应力校核强度，必要时选择大一号或 大二号旳工字钢； u 若剪力较大时，还需校核剪切强度。
按第四强度理论
Qy My T
r4
1 W
Mz Qz
M 2 0.75T 2 47.4 MPa [ ]
(3) 曲柄旳强度计算
l 危险截面 III-III截面
l 计算内力 u 取下半部分
Qx Qz
N R2 C1 13 kN Mx m H2 d /2
765 Nm
M z R2 (a b / 2) 660 Nm
横截面上任意一点 （ z, y） 处旳正应 力计算公式为
1.拉伸正应力
FN
A
2.弯曲正应力
Mz y
Iz
FN Mz y
A Iz
( z,y)
Mz
z
O
x
FN
y
3.危险截面旳拟定
作内力图
F1
轴力
《材料力学组合变形》课件
这种变形通常发生在承受轴向力 和弯矩的杆件中，其变形特点是 杆件既有伸长或缩短，又有弯曲 。
拉伸与压缩组合变形的分析方法
01
02
03
弹性分析方法
基于弹性力学的基本原理 ，通过求解弹性方程来分 析杆件内部的应力和应变 分布。
塑性分析方法
在材料进入塑性阶段后， 采用塑性力学的基本理论 来分析杆件的承载能力和 变形行为。
材料力学在组合变形中的应用实例
01
02
03
04
桥梁工程
桥梁的受力分析、桥墩的稳定 性分析等。
建筑结构
高层建筑、大跨度结构的受力 分析、抗震设计等。
机械工程
机械零件的强度、刚度和稳定 性分析，如轴、轴承、齿轮等
。
航空航天
飞机和航天器的结构分析、材 料选择和制造工艺等。
材料力学在组合变形中的发展趋势
特点
剪切与扭转组合变形具有复杂性和多样性，其变形行为受到多种因素的影响，如 材料的性质、杆件的长度和截面尺寸、剪切和扭转的相对大小等。
剪切与扭转组合变形的分析方法
1 2 3
工程近似法
在分析剪切与扭转组合变形时，通常采用工程近 似法，通过简化模型和假设来计算杆件的应力和 变形。
有限元法
有限元法是一种数值分析方法，可以模拟杆件在 剪切与扭转组合变形中的真实行为，提供更精确 的结果。
弯曲组合变形的分析方法
叠加法
刚度矩阵法
叠加法是分析弯曲组合变形的基本方 法之一。该方法基于线性弹性力学理 论，认为各种基本变形的应力、应变 分量可以分别计算，然后按照线性叠 加原理得到最终的应力、应变分布。
刚度矩阵法是通过建立物体内任意一 点的应力、应变与外力之间的关系， 来求解复杂变形问题的一种方法。对 于弯曲组合变形，可以通过构建系统 的刚度矩阵来求解。
拉伸与压缩组合变形的分析方法
01
02
03
弹性分析方法
基于弹性力学的基本原理 ，通过求解弹性方程来分 析杆件内部的应力和应变 分布。
塑性分析方法
在材料进入塑性阶段后， 采用塑性力学的基本理论 来分析杆件的承载能力和 变形行为。
材料力学在组合变形中的应用实例
01
02
03
04
桥梁工程
桥梁的受力分析、桥墩的稳定 性分析等。
建筑结构
高层建筑、大跨度结构的受力 分析、抗震设计等。
机械工程
机械零件的强度、刚度和稳定 性分析，如轴、轴承、齿轮等
。
航空航天
飞机和航天器的结构分析、材 料选择和制造工艺等。
材料力学在组合变形中的发展趋势
特点
剪切与扭转组合变形具有复杂性和多样性，其变形行为受到多种因素的影响，如 材料的性质、杆件的长度和截面尺寸、剪切和扭转的相对大小等。
剪切与扭转组合变形的分析方法
1 2 3
工程近似法
在分析剪切与扭转组合变形时，通常采用工程近 似法，通过简化模型和假设来计算杆件的应力和 变形。
有限元法
有限元法是一种数值分析方法，可以模拟杆件在 剪切与扭转组合变形中的真实行为，提供更精确 的结果。
弯曲组合变形的分析方法
叠加法
刚度矩阵法
叠加法是分析弯曲组合变形的基本方 法之一。该方法基于线性弹性力学理 论，认为各种基本变形的应力、应变 分量可以分别计算，然后按照线性叠 加原理得到最终的应力、应变分布。
刚度矩阵法是通过建立物体内任意一 点的应力、应变与外力之间的关系， 来求解复杂变形问题的一种方法。对 于弯曲组合变形，可以通过构建系统 的刚度矩阵来求解。
材料力学10组合变形
材料力学10组合变形组合变形是指当结构受到外力作用时，由于各个零件的不同材料及尺寸性质的差异，导致各个零件产生不同的变形现象，从而使整个结构发生整体的变形。
组合变形是结构力学的重要内容，对于工程结构的设计、安全性评估和结构稳定性分析都至关重要。
本文将介绍组合变形的概念、分析方法和影响因素。
组合变形的概念：组合变形是指由于结构中不同零件的尺寸和材料性质的不一致，而导致结构在受力时产生的整体变形。
组合变形分为两类：一是刚体体变形，即结构在受力作用下整体平移、旋转或缩放；二是构件本身变形，即结构中各零件由于尺寸和材料的不一致而产生的内部变形。
组合变形的分析方法：组合变形的分析方法主要有两种：力法和位移法。
力法是指根据梁的变形方程和杨氏模量的定义，通过计算各零件在各个截面上的张力或弯矩，从而得到整体的变形情况。
位移法是指根据构件的位移和应变关系，通过求解位移方程组，从而得到整体的变形情况。
力法和位移法都是基于弹性理论，适用于较小变形和线性弹性材料的情况。
组合变形的影响因素：组合变形的大小与结构的几何形状、零件尺寸和材料性质有关。
影响组合变形的因素主要有以下几个方面：1.结构的几何形状：结构的几何形状对组合变形有重要影响。
例如，在长梁的弯曲变形中，梁的长度和曲率半径都会影响变形的大小。
2.零件的尺寸：零件的尺寸对组合变形有重要影响。
例如，在梁的弯曲变形中，梁的截面积和转动惯量会影响变形的大小。
3.零件的材料性质：零件的材料性质对组合变形有重要影响。
例如，在梁的弯曲变形中，梁的弹性模量和截面剪切模量会影响变形的大小。
4.外力的作用方式：外力的作用方式对组合变形有重要影响。
例如，在梁的弯曲变形中，集中力和均布力对变形的影响是不同的。
除了以上几个因素外，结构的边界条件和连接方式也会影响组合变形的大小。
此外，在实际工程中，结构中可能存在的缝隙、温度变化、材料老化等因素也会对组合变形产生影响。
对于设计工程结构来说，合理控制组合变形是非常重要的。
14-1组合变形-材料力学
Fz F sin
五、自由端的变形
z
A
y
y
FL3 cos
3EI z
z
B y
x
B z
FL3 sin
3EI y
B
z
y
查表7-1（3）
在 Fz B点的位移 z ：
例题14.1 图所示屋架结构。已知屋面坡度为1：2， 两屋架之间的距离为4m，木檩条梁的间距为1.5m， 屋面重（包括檩条）为1.4kN/m2。若木檩条梁采
"
Iy
Iy
'
M z y M y z
Iz
Iy
cos sin
M ( y z)
Iz
Iy
四、斜弯曲时的强度条件
1、中性轴的位置
M (
Iz
yo
sin
Iy
zo )
0
tan yo Iz tan
zo
和扭矩图如图c、d
危险截面在杆的根部（固定端）
（3）应力分析
B
M W
T
T Wp
在杆的根部取一单元体分析
y 0, x B , xy T
计算主应力
1
3
B
2
( B
2
)2
2 T
2 0
（4）强度分析
选择第三、第四强度理论
r3
入偏心拉伸的强度条
4
32
件校核
32.4106 32.4MPa 35MPa
满足强度条件，最后选用立柱直 d = 12.5cm
材料力学课件第8章组合变形zym
§8—4 扭转与弯曲的组合 一、圆截面杆弯扭组合 实例： （一）实例： 已知：塑性材料轴尺寸，传动力偶Me。 已知：塑性材料轴尺寸，传动力偶 。 试建立轴的强度条件。 试建立轴的强度条件。 解： 1、确定危险点： 、确定危险点： （1）外力分析 ） F 计算简图： ①计算简图： Fτ 由 ∑ M x = 0 得： FD = Me 2 可确定F 由F可确定 τ。 可确定 外力分解： ②外力分解： 变形判断： ③变形判断： AB段扭转变形，BE段弯扭组合变 段扭转变形， 段弯扭组合变 段扭转变形 形，EC段弯曲变形。 段弯曲变形。 段弯曲变形
解： 、确定各边为中性轴时的压力作用点： 1、确定各边为中性轴时的压力作用点： b2 h2 2 iy = , iz2 = 12 12 h az = ∞ AB截距： a y = − , 截距： 截距 2 h2 iz2 12 = h , zF = 0 F作用点 坐标： yF = − = − 作用点a坐标 作用点 坐标： h 6 ay − 2 同样确定b,c,d点。 同样确定 点 2、连线 确定截面核心。 、连线a,b,c,d确定截面核心。 确定截面核心 解：
3 由： W ≥ M max = 12 ×10 N ⋅ m 6
[σ ]
100 × 10 Pa
= 12 × 10−5 m3 = 120cm3
查表选定16号工字钢。 查表选定 号工字钢。 号工字钢 （2）组合变形校核计算： ）组合变形校核计算： 16号工字钢：W=141cm3,A=26.1cm3 号工字钢： 号工字钢
2、应力状态分析 、 均为单向应力状态 单向应力状态。 均为单向应力状态。
'' σ A = σ ′ +σ A =
F (0.425m) F × (0.075m) + −3 2 15 ×10 m 5310 ×10−8 m 4
材料力学 第7章 组合变形
y
1
z x
1
式中M——危险截面的弯矩 T——危险截面的扭矩
2
y
2
例 3 某齿轮传动轴上装有两个直圆柱齿轮，C轮的输入功
率NkC=15kW，不考虑功率损耗，轴的转速n=850r/min， 直径d=50mm，材料的[]=50MPa，两轮节圆直径分别为 D1=300mm， D2=120mm，压力角=20，试校核轴的强度。
FAx
800
.
D
.
A
.
. .
C
.
B 1500
2500
c max
FN M max A Wz
A FAy y
FC
FCx
FCy C
F B
F x
40 10 12 10 4 26.1 10 141 10 6
3 3
FN 40kN
12kNm M
100.5 MPa [ ]
第七章
作业
7-2 7-4 7-5 7-8 7-13 7-17 7-21
第七章
7.1 7.2
组合变形杆的强度
组合变形的概念 弯曲与拉伸（压缩）的组合
7.3
偏心压缩与截面核心
7.4 扭转与弯曲的组合 7.5 复合梁的强度计算
7.6
开口薄壁梁的切应力
组合变形杆的强度
7.1
组合变形概念
F
截面核心—— 在轴向压力作用下，使杆的横截面上只产 生压应力的载荷作用区域
偏心压缩与截面核心
五、截面核心
2.确定方法
压力作用区域。 当压力作用在此区域内时，横截面上无拉应力。 ay 截面核心 az
1
z x
1
式中M——危险截面的弯矩 T——危险截面的扭矩
2
y
2
例 3 某齿轮传动轴上装有两个直圆柱齿轮，C轮的输入功
率NkC=15kW，不考虑功率损耗，轴的转速n=850r/min， 直径d=50mm，材料的[]=50MPa，两轮节圆直径分别为 D1=300mm， D2=120mm，压力角=20，试校核轴的强度。
FAx
800
.
D
.
A
.
. .
C
.
B 1500
2500
c max
FN M max A Wz
A FAy y
FC
FCx
FCy C
F B
F x
40 10 12 10 4 26.1 10 141 10 6
3 3
FN 40kN
12kNm M
100.5 MPa [ ]
第七章
作业
7-2 7-4 7-5 7-8 7-13 7-17 7-21
第七章
7.1 7.2
组合变形杆的强度
组合变形的概念 弯曲与拉伸（压缩）的组合
7.3
偏心压缩与截面核心
7.4 扭转与弯曲的组合 7.5 复合梁的强度计算
7.6
开口薄壁梁的切应力
组合变形杆的强度
7.1
组合变形概念
F
截面核心—— 在轴向压力作用下，使杆的横截面上只产 生压应力的载荷作用区域
偏心压缩与截面核心
五、截面核心
2.确定方法
压力作用区域。 当压力作用在此区域内时，横截面上无拉应力。 ay 截面核心 az
材料力学- 8组合变形
l/2 l/2
D
A P
C
d
B
Q
l/2
D
l/2
解：
B
A P
mA
C
Q Q 1 mC QD 2 A M C
Ql/4
B
（1）受力分析与计算简 图：将载荷Q向轮心平移 （2）内力分析，画出弯 矩图和扭矩图；找出危险 面和危险点：危险面在中 点C处 （3）代公式：求最大安 全载荷Q
d
T
QD/2
r3
设计中常采用的简便方法：
因为偏心距较大，弯曲应力 是主要的，故先考虑按弯曲强 度条件 设计截面尺寸
M Wz 6000 6 35 10 d 3 32
解得立柱的近似直径 取d=12.5cm,再代 入偏心拉伸的强 度条件校核
d 0.12 m
15000 6000 3.14 0.1252 3.14 0.1253 4 32 32.4 106 32.4MPa 35MPa
M 2 T2 [ ] Wz
l/2
D
l/2
Ql Q M 0.8 0.2Q 4 4
B
A P
mA
C
d
T
Q Q 1 mC QD 2 A M C
Ql/4
QD Q 0.36 0.18Q 2 2
r3
B
M 2 T2 [ ] Wz
Wz
ቤተ መጻሕፍቲ ባይዱ 3
32
T
QD/2
（1）计算内力
将立柱假想地截开，取上段为 研究对象，由平衡条件，求出 立柱的轴力和弯矩分别为
F
N
FN P 15000 N M Pe 15000 0.4 6000N m
D
A P
C
d
B
Q
l/2
D
l/2
解：
B
A P
mA
C
Q Q 1 mC QD 2 A M C
Ql/4
B
（1）受力分析与计算简 图：将载荷Q向轮心平移 （2）内力分析，画出弯 矩图和扭矩图；找出危险 面和危险点：危险面在中 点C处 （3）代公式：求最大安 全载荷Q
d
T
QD/2
r3
设计中常采用的简便方法：
因为偏心距较大，弯曲应力 是主要的，故先考虑按弯曲强 度条件 设计截面尺寸
M Wz 6000 6 35 10 d 3 32
解得立柱的近似直径 取d=12.5cm,再代 入偏心拉伸的强 度条件校核
d 0.12 m
15000 6000 3.14 0.1252 3.14 0.1253 4 32 32.4 106 32.4MPa 35MPa
M 2 T2 [ ] Wz
l/2
D
l/2
Ql Q M 0.8 0.2Q 4 4
B
A P
mA
C
d
T
Q Q 1 mC QD 2 A M C
Ql/4
QD Q 0.36 0.18Q 2 2
r3
B
M 2 T2 [ ] Wz
Wz
ቤተ መጻሕፍቲ ባይዱ 3
32
T
QD/2
（1）计算内力
将立柱假想地截开，取上段为 研究对象，由平衡条件，求出 立柱的轴力和弯矩分别为
F
N
FN P 15000 N M Pe 15000 0.4 6000N m
材料力学——8组合变形
A
F m
B
T 15kN m
M max 20kN m
W
15kN· m
D 3
32
(1 )
4
+
r3
20kN· m
-
M2 T2 157.26MPa [ ] W
例题8 传动轴如图所示。在A处作用一个外力偶矩
m=1kN· m，皮带轮直径 D=300mm，皮带轮紧边拉力为 F1，松边拉力为F2。且F1=2F2，L=200mm，轴的许用 应力[]=160MPa。试用第三强度理论设计轴的直径
例3 直径为d=0.1m的圆杆受力如图,T=7kNm,P=50kN, []=100MPa,试按第三强度理论校核此杆的强度。 解：拉扭组合,危险点应力状态如图 T P A T P
P 450 10 3 6.37 MPa A 0.12
T 167000 35 .7MPa 3 Wn 0.1
P
P
1
1
a a
a a
未开槽前 立柱为轴向压缩
N P P P 1 2 A A (2a) 4a2
开槽后 立柱危险截面为偏心压缩;
P
1
P
1
a a
a a
P
1
Pa/2
1
N M P Pa 2 2P 2 2 A W 2 a a 1 2a 2 a a 6 2 P a2 开槽后立柱的最大压应力 8 2 P 4a 未开槽前立柱的最大压应力
2、相当应力计算 第三强度理论,计算相当力
2 0
r 3 1 3 2 4 2
第四强度理论,计算相当应力
r 4 2 3 2
3、强度校核
F m
B
T 15kN m
M max 20kN m
W
15kN· m
D 3
32
(1 )
4
+
r3
20kN· m
-
M2 T2 157.26MPa [ ] W
例题8 传动轴如图所示。在A处作用一个外力偶矩
m=1kN· m，皮带轮直径 D=300mm，皮带轮紧边拉力为 F1，松边拉力为F2。且F1=2F2，L=200mm，轴的许用 应力[]=160MPa。试用第三强度理论设计轴的直径
例3 直径为d=0.1m的圆杆受力如图,T=7kNm,P=50kN, []=100MPa,试按第三强度理论校核此杆的强度。 解：拉扭组合,危险点应力状态如图 T P A T P
P 450 10 3 6.37 MPa A 0.12
T 167000 35 .7MPa 3 Wn 0.1
P
P
1
1
a a
a a
未开槽前 立柱为轴向压缩
N P P P 1 2 A A (2a) 4a2
开槽后 立柱危险截面为偏心压缩;
P
1
P
1
a a
a a
P
1
Pa/2
1
N M P Pa 2 2P 2 2 A W 2 a a 1 2a 2 a a 6 2 P a2 开槽后立柱的最大压应力 8 2 P 4a 未开槽前立柱的最大压应力
2、相当应力计算 第三强度理论,计算相当力
2 0
r 3 1 3 2 4 2
第四强度理论,计算相当应力
r 4 2 3 2
3、强度校核
《材料力学》第八章组合变形
解 (1)外力分析，确定变形类型—拉弯组合；
（2）内力分析，确定危险截面—整个轴；
M=600(kN·cm) FN=15(kN)
(3)应力计算，确定危险点—ａ、b点；
P产生拉伸正应力： t
FN AFNd 2源自4FNd 24
M拉产弯生组弯合曲：的正应力：wmax
M Wy
M
d3
32
32M
d3
P M= a Pe
补例8.1 已知： P=2kN,L求=：1mσm,Iazx=628×104mm4,Iy=64×1040mm2740 2844
解:1.分解P力。 Py Pcos φ Pz Psin φ 2．画弯矩图，确定危险截面--固定端截面。 3．画应力分布图，确定危险点—A、 B点
σ” σ’
A
x
y
Pyl
M
z
践中，在计算中，往往忽略轴力的影响。
4.大家考虑扭转、斜弯曲与拉（压）的组合怎么处理？
例8.5 图8.14a是某滚齿机传动轴AB的示意图。轴的直径为35 mm，材料为45钢， [σ]=85 MPa。轴是由P=2.2kW的电动机通过
带轮C带动的，转速为n=966r／min。带轮的直径为D=132 mm，
Mz Py l - x Pcosφ l - x Mcosφ My Pz l - x Psinφ l - x Msinφ
式中的总弯矩为：M Pl- x
3.计算两个平面弯曲的正应力。在x截面上任取一点A(z 、y)，
与弯矩Mz、My对应的正应力分别为σ’和σ”，故
- Mz y , - M yz
第八章 组合变形
基本要求: 掌握弯曲与拉伸（或压缩）的组合、扭转与弯曲的组合 的强度计算。
重点： 弯曲与拉伸（或压缩）的组合，扭转与弯曲的组合。
（2）内力分析，确定危险截面—整个轴；
M=600(kN·cm) FN=15(kN)
(3)应力计算，确定危险点—ａ、b点；
P产生拉伸正应力： t
FN AFNd 2源自4FNd 24
M拉产弯生组弯合曲：的正应力：wmax
M Wy
M
d3
32
32M
d3
P M= a Pe
补例8.1 已知： P=2kN,L求=：1mσm,Iazx=628×104mm4,Iy=64×1040mm2740 2844
解:1.分解P力。 Py Pcos φ Pz Psin φ 2．画弯矩图，确定危险截面--固定端截面。 3．画应力分布图，确定危险点—A、 B点
σ” σ’
A
x
y
Pyl
M
z
践中，在计算中，往往忽略轴力的影响。
4.大家考虑扭转、斜弯曲与拉（压）的组合怎么处理？
例8.5 图8.14a是某滚齿机传动轴AB的示意图。轴的直径为35 mm，材料为45钢， [σ]=85 MPa。轴是由P=2.2kW的电动机通过
带轮C带动的，转速为n=966r／min。带轮的直径为D=132 mm，
Mz Py l - x Pcosφ l - x Mcosφ My Pz l - x Psinφ l - x Msinφ
式中的总弯矩为：M Pl- x
3.计算两个平面弯曲的正应力。在x截面上任取一点A(z 、y)，
与弯矩Mz、My对应的正应力分别为σ’和σ”，故
- Mz y , - M yz
第八章 组合变形
基本要求: 掌握弯曲与拉伸（或压缩）的组合、扭转与弯曲的组合 的强度计算。
重点： 弯曲与拉伸（或压缩）的组合，扭转与弯曲的组合。
材料力学第8章组合变形
MB
M
2 yB
M
2 zB
(364 N m)2 (1000N m)2 1064N m
•由Mz图和My图可知， B截面上的总弯矩最大， 并且由扭矩图可见B截 面上的扭矩与CD段其 它横截面上相同，TB ＝-1000 N·m，于是判 定横截面B为危险截面。
3. 根据MB和TB按第四强度理论建立的强度条件为
Wp
r4
M 2 0.75T 2
W
300N.m 1400N
300N.m
1500N 200
150
300N.m
128.6N.m
120N.m
（2）作内力图
危险截面E 左处
T 300N.m
M
M
2 y
M
2 z
176N.m
（3）由强度条件设计d
r3
M2 T2 W
W d 3
32
32 M 2 T 2
第8章 组合变形
8.1 组合变形和叠加原理 8.2 拉伸或压缩与弯曲的组合 8.3 偏心压缩和截面核心 8.4 扭转与弯曲的组合 8.5 组合变形的普遍情况
8.1 组合变形和叠加原理
组合变形——实际构件由外力所引起的变形包含两种或两 种以上的基本变形。如压力框架、烟囱、传动轴、有吊车 的立柱。 叠加原理——如果内力、应力、变形等与外力成线性关系， 则在小变形条件下，复杂受力情况下组合变形构件的内力， 应力，变形等力学响应可以分成几个基本变形单独受力情 况下相应力学响应的叠加，且与各单独受力的加载次序无 关。 前提条件：
即 亦即 于是得
r4
M 2 0.75T 2 [ ]
W
•请同学们按
照第三强度理 (1064 N m)2 0.75(1000 N m)2 100106 Pa W
材料力学第八章-组合变形
12 103 141106
94.3MPa 100MPa
故所选工字钢为合适。
材料力学
如果材料许用拉应力和许用压应力不 同，且截面部分 区域受拉，部分区域 受压，应分别计算出最大拉应力 和最 大压应力，并分别按拉伸、压缩进行 强度计算。
材料力学
=+
材料力学
t,max
=+
t,max
①外力分析：外力向形心简化并沿主惯性轴分解。
②内力分析：求每个外力分量对应的内力方程和 内力图，确定危险面。
③应力分析：画危险面应力分布图，叠加，建立 危险点的强度条件。
一般不考虑剪切变形；含弯曲组合变形，一般以弯
曲为主，其危险截面主要依据Mmax，一般不考虑弯
曲切应力。
材料力学
四.叠加原理
构件在小变形和服从胡克定律的条件下， 力的独立性原理是成立的。即所有载荷作用 下的内力、应力、应变等是各个单独载荷作 用下的值的代数和。
材料力学
F F
350
150
y
50 z
50 150 z0 z1
显然，立柱是拉伸和弯曲的 组合变形。
1、计算截面特性（详细计算略） 面积 A 15103 m2
z0 75mm I y 5310 cm4
材料力学
2、计算内力 取立柱的某个截面进行分析
FN F
M (35 7.5) 102 F 42.5102 F
组合变形
§8.1 组合变形和叠加原理 §8.2 拉伸或压缩与弯曲的组合 §8.3 偏心压缩和截面核心 §8.4扭转与弯曲的组合
content
1、了解组合变形杆件强度计算的基本方法 2、掌握拉（压）弯组合变形和偏心拉压杆 件的应力和强度计算 3、掌握圆轴在弯扭组合变形情况下的强度 条件和强度计算
材料力学：第11章：组合变形
2
≤[σ]
2
M + 0.75T W
3
≤[σ]
πd
32
例：图示悬臂梁的横截面为等边三角形， 图示悬臂梁的横截面为等边三角形， C为形心，梁上作用有均布载荷ｑ，其作用方 为形心，梁上作用有均布载荷ｑ，其作用方 为形心 ｑ， 向及位置如图所示，该梁变形有四种答案： 向及位置如图所示，该梁变形有四种答案： A）平面弯曲； （√ ）平面弯曲； （C）纯弯曲； ）纯弯曲； （B）斜弯曲； ）斜弯曲； （D）弯扭结合。 ）弯扭结合。
Mz y My σ′=− =− sin ϕ Iz Iz
σ ′′ = −
ቤተ መጻሕፍቲ ባይዱ
My z Iy
Mz =− cos ϕ Iy
Py
Mz
Pz
My
y z σ = σ ′ + σ ′′ = − M sin ϕ + cos ϕ I Iy z
下面确定中性轴的位置： 下面确定中性轴的位置： 设中性轴上某一点的坐标为 y0 、 z0，则
α
ϕ
中性轴
ϕ
中性轴
二、位移计算 斜弯曲概念 为了计算梁在斜弯曲时的挠度， 为了计算梁在斜弯曲时的挠度，仍应用叠加法
fy = Py l
3
3EI Z
Pl3 = sin ϕ 3EI Z
Pl3 Pz l 3 fz = = cosϕ 3EI y 3EI y
ϕ
f =
2 fy
+f
2 z
tg β =
fy fz
=
Iy Iz
tg ϕ
tg β = tgα
α
β =α
ϕ
中性轴 总挠度f与中 总挠度 与中 性轴垂直
材料力学组合变形
材料力学组合变形材料力学是研究材料在外力作用下的力学性能和变形行为的学科。
组合变形是指将不同的材料组合在一起，并在外力作用下共同发生变形。
本文将探讨材料力学中的组合变形及其应用。
材料的组合变形主要有两种形式，即均匀变形和非均匀变形。
均匀变形是指组合材料中各个组分材料的变形均匀一致，不发生相对滑动或相对滑动微小。
在均匀变形中，组合材料的整体变形主要由各个组分材料的线弹性或体弹性共同引起。
例如，当钢筋混凝土受到拉力作用时，钢筋和混凝土发生均匀的拉伸变形。
非均匀变形是指组合材料中各个组分材料的变形不一致，发生相对滑动或相对滑动巨大。
在非均匀变形中，组合材料的整体变形主要由各个组分材料的弹性、塑性和断裂等共同引起。
例如，当金属板与橡胶层组合时，金属板可以发生弯曲变形，而橡胶层则可以发生弹性变形和形变。
组合变形在实际应用中有着广泛的应用。
首先，组合变形可以通过调节组分材料的比例和形状来实现特定的力学性能。
例如，通过调节纤维增强复合材料中纤维的方向和分布，可以显著改变其强度和刚度。
此外，通过组合不同的材料，还可以实现热膨胀系数匹配、界面应力分散等功能，从而降低材料的应力集中和断裂风险。
其次，组合变形还可以实现材料的远程感应和控制。
例如，利用形状记忆合金和橡胶组合的智能材料，在外力作用下可以实现形状变化和应变分布的调控。
这种材料可以应用于自适应结构、智能传感器等领域。
此外，通过组合不同的材料，还可以实现流变性能的调控，进而应用于动态振动控制等领域。
最后，组合变形还可以实现材料的多功能性和复合性能。
通过组合不同材料的优势，可以实现多功能材料的设计和制备。
例如，通过合理选择纳米材料和纤维增强复合材料等，可以实现具备高强度、低密度、耐热和导电等多种特性的复合材料。
此外，通过组合不同材料的力学性能，还可以实现弹性材料、减振材料和防护材料的设计与制备。
综上所述，材料力学中的组合变形是一种重要的力学现象，具有广泛的应用前景。
29-31材料力学-组合变形
P 200 图. （2）
dP
P M
1maxAP1
M Wz1
350000350506
0.20.3 0.20.32
11.7M Pa
2max
P A
3 5 0 0 0 08.7 5MP a 0.20.2
15
[例5] 图示钢板受力P=100kN，试求最大正应力；若将缺口
移至板宽的中央，且使最大正应力保持不变，则挖空宽度为多
结果表明，最大压应力与许用应力接近相等，故无需重新 选取截面的型号。
11
二、偏心拉伸(压缩)
如果外力的作用线平行于杆件的轴线，但不通过杆件横截
面的形心，则将引起偏心拉伸(压缩)。
1、分解： P
x P y
z My
x z Mz
Py My
12
2、应力分析：
x z Mz P y
P
MZ
z
My y
My
xP
P A
发生最大拉应力，且
tmax
tmax
在截面的外侧边缘上发生最大压应力，且 cmaxcmax
最后，由抗拉强度条件 得
F P ≤ 45.1kN。
由抗压强度条件得
F P ≤ 171.3kN
为使立柱同时满足抗拉和抗压强度条件，压力FP不应超过
45.1kN 。
20
[例7] 方形截面杆的横截面面积在 mn 处减少一半，试求由轴
30
弯扭组合问题的求解步骤：
① 外力分析：外力向形心简化并分解。 ② 内力分析：每个外力分量对应的内力方程和内力图，确定
危险面。 ③应力分析：建立强度条件。
r3
My2 Mz2 Mn2 W
r4
My2Mz20.7 5Mn2 W
材料力学组合变形
材料力学组合变形材料力学是指材料在受力作用下产生的力学变形过程，组合变形是指在材料受到多个作用力时产生的整体力学变形过程。
材料力学组合变形是研究材料在受到多个作用力时的变形行为。
在材料力学中，材料的力学行为可以通过弹性模量、屈服强度、断裂强度等参数来描述。
当材料受到作用力时，会发生弹性变形和塑性变形。
弹性变形是指材料在受力后恢复到原始形状的变形；而塑性变形是指材料在受力后不完全恢复到原始形状的变形。
对于组合变形而言，材料会受到多个作用力，因此其变形行为会更为复杂。
组合变形中，作用在材料上的多个力可以是同方向的也可以是不同方向的。
如果作用在材料上的力是同方向的，材料会受到共同作用力的影响，从而发生整体变形。
例如，在拉伸材料时，受到的力方向是相同的，材料会发生拉伸变形。
而如果作用在材料上的力是不同方向的，材料会受到不同方向的作用力，从而引起复杂的变形。
例如，在压缩材料时，受到的力方向是不同的，材料会发生挤压变形。
组合变形中，材料不仅会发生弹性变形和塑性变形，还会发生刚塑性变形和刚塑性折断。
刚塑性变形是指材料在受到力后发生弹性变形和塑性变形之前的刚性变形。
而刚塑性折断是指材料在受到力后发生弹性变形和塑性变形之后的断裂行为。
这些变形与断裂行为的发生受到材料的性质和作用力的大小和方向等因素的影响。
组合变形也可以通过应变和位移来描述。
应变是指材料单位长度或单位体积的变化，是描述材料变形的量度。
位移是指材料单位长度或单位体积的实际变化，是描述材料移动的量度。
通过应变和位移的变化，可以对材料力学组合变形进行分析和计算，从而得到材料变形的性质和行为。
总之，材料力学组合变形是材料在受到多个作用力时产生的整体力学变形过程。
通过研究材料的力学行为，可以了解材料在不同作用力下的变形行为，并进一步应用于工程设计和材料选择等领域。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
max
N A
M
2 z
M
2 y
[ ]
W
例4： 一 个拉伸试件载荷为P=80kN , 截面为1080mm2,
的矩形，加工好以后发现试件上缘有裂缝 ,为防止裂纹
在应力集中下扩展，在试件上部挖去一个r =10mm 的半
圆孔，试校核其强度 。如果强度不够，可采取什么措施
补救？[]=140MPa
r P
P解：无挖裂去纹小时孔后:
度条件。
§8-2 拉伸(压缩)与弯曲的组合作用
轴向拉压：外力的合力作用线与杆的轴线重合。 偏心拉压:外力的合力作用线与杆的轴线不重合。
偏心拉压问题的解题方法：在危险截面，将合力平移，使其 通过截面形心。问题简化为
偏心拉压 = 轴向拉压 + 弯曲
Y
P
1、危险截面—离集中力P较远的任 意截面均为危险截面。
②分别独立计算各种基本变形，然后叠加。
（假设：各个基本变形互不影响）
4.实例：
P
P z
R
x
M
y
P
P q
hg
水坝
5.组合变形的研究方法 —— 叠加原理
①外力分析：外力向形心(或弯心)简化并沿主惯性轴分解 ②内力分析：求每个外力分量对应的内力方程和内力图，确
定危险面。 ③应力分析：画危险面应力分布图，叠加，建立危险点的强
无论什么材料，只有一个危险点即：最大拉应力点。
偏心压缩时，最大拉应力σTmax < 最大压应力σCmax ，
对于塑性材料，只有一个危险点即：最大压应力点。
对于脆性材料，则有两个危险点即：最大压应力点和最大拉应 力点。
最大拉、压应力：
拉/压 N M max （拉为正，压为负）
max
强度条件：
A Wz
N M max [ ]
A WZ max
(对脆性材料，要区分[T ]和[C ])
基本工作： ①安全校核 ②截面设计 ③确定承载力
例1：AB为工字梁[ ] 100MPa ，试选工字梁型号。
0.8m
D
T
A
H
2.5m
V CB
P=8kN 1.5m
tan 0.8
2.5
解：(1) 求V,H
由 M A 0 V 2.5 P (2.5 1.5) 0
力危 状险 态点
为 单 向 应
z
危险点的强度条件
C max
中
C max
性
轴
T max
z
T max
Cmax ( y) (z) C
Mz Wz
My Wy
N A
C
T max ( y) (z) C
（ M z Wz
My Wy
-
N ） A
T
y 横截面尺寸 b
几 何
性
h
质
Wz
bh2 6
Z
e 2、将力P向截面形心平移
l
P
P
偏心拉压 = 轴向拉压 + 弯曲
e
M
M z Pe
NP
N
A
Mz y
Iz
确定危险点：将应力叠加，找出最大应力σmax的作用点
结果
max
N A
Mz Wz
(拉，在最上沿的各点)
或者
偏心拉压时，中性轴不再过截面形 心，甚至没有中性轴。
注意：偏心拉伸时，最大拉应力σTmax > 最大压应力σCmax ，
一、斜弯曲：杆件弯曲后，挠曲线与外力（横向力）不共面。
二、斜弯曲的研究方法 ： 1.分解：将外载沿横截面的两个形心主轴分解，于是得到两
个正交的平面弯曲（双向弯）。 2.横截面为矩形或工字形（有棱角），则先计算应力后叠加：先
P P
P A
Mz
z
Mz wz
My
y
My wy
p
z
z
y
y
My=P ·zP
c
P z •叠加求最大压应力和最大拉应力
Mz=P
C/T (y) (z) C
·yP y
P yp Pzp P
z
wz
wy A
y
(y)
y
(z)
危险点的应力状态
中 性 轴
T max
C max
C max
T max
，Wy
hb2 6
例3：结构如图，在端部Py过形心且与沿y轴方向，在中部Pz过形心 且与沿z轴方向。尺寸如图。
求此梁的最大应力。
Pz
z
H
y L
x Py
解：对于圆截面杆，在危险截面的形心处，分解出与基
本变形对应的载荷，将绕Y轴和Z轴的弯矩My、Mz用
双箭头矢量表示，然后按照矢量合成的方法，计算出
合弯矩M：，根据弯曲应力的分布规律，可以找到危 险点。
Mz=PyL
M
M
2 y
M
2 z
My=PzH x
最大拉应力σT
Pz
z
H
y L
Py
z
Mz
最大压应力σC
My
M
y 中性轴
Mz=PyL
M
M
2 y
M
2 z
My=PzH x
最大拉应力σT
Pz
z
H
y L
Py
z
Mz
最大压应力σC
My
M
y 中性轴
如果在危险截面的危险点处，还有轴向的拉（压） 应力，则还要进一步迭加，最后进行强度校核。
P A
100MPa
r
e r 2 N P MZ Pe P r 2
bP
N N P 114MPa
MZ
A (b r)t
t
对称
挖孔
(b
P 2r)t
MZ WZ
Pr 2 (b r)2t
6
4
max
114
49 163MPa
强度不够！
§8–3 斜弯曲
§8-1 组合变形的概念和实例
1.基本变形：
①拉伸、压缩 ②扭转 ③弯曲
2.组合变形：
在复杂外载作用下，构件的变形会包含几种 简单变形，当几种变形所对应的应力属同一量 级时，不能忽略之，这类构件的变形称为组合 变形。
3.组合变形问题的处理方法:
叠加原理（条件:小变形）。
①将荷载分解简化成与基本变形对应的等 效静力荷载。
查表P324 16号 W=141cm3 A=26.1cm2
②考虑N，M作用校核：
max
N M max A Wz
40 103 26.1 104
12 103 141 104
100.5MPa [ ] 100MPa
100.5 100 0.5% 16号工字钢满足要求
100
例2：脆性材料偏心压缩
基本方法：通过将偏心的载荷二次平移到截面形心，
得到简单变形的迭加形式
Pz
zP
A
y
My=P·zP
PP z y
yP
My=P·zP
PP z
Mz=P·yP y
•基本变形应力计算
My=P·zP
P z
Mz=P·yP y
(y) Mz Pyp
wz
wz
(z) M y P zp
wy
wy
C
P A
危险截面上的各种应力分布
V 12.8kN
(2) 内力图
H V 40kN
tan
D
0.8m
A 2.5m
CB P=8kN
1.5m
12 40
M kN·m N kN
(3) 选型号：一般弯曲应力远大于拉压应力，可以先按照弯曲 强度试算。
①由 Mmax选：
W
M max
[ ]
12 103 100 106
12 105 m3 120cm3