材料力学(单辉祖)第十章组合变形
第10章-组合变形

应力状态-单向+纯剪切 强度条件(塑性材料)
2 r3 M N 4 T [ ] 2 2 r4 M N 3 T [ ] 2
单辉祖:材料力学教程
15
例 题
例10-3 图示钢质传动轴,Fy = 3.64 kN, Fz= 10 kN, F’z =1.82 kN, F’y = 5 kN, D1 = 0.2 m, D2 = 0.4 m, [] = 100 MPa, 轴径 d=52 mm, 试按第四强度理论校核轴的强度
③ 将所得结果叠加,即得杆件组合变形时的应力。
单辉祖:材料力学教程 5
§2 弯拉(压)组合 §3 偏心压缩
弯拉(压)组合 例题
偏心压缩
单辉祖:材料力学教程
6
弯拉(压)组合
产生弯曲与轴向拉压的组合变形的情况:
杆上除作用有横向力外,同时还作用有轴向力; 外力作用线虽然平行于杆轴,但不通过截面形心。
max
8.66 103 N 8.27 103 N m 111.5MPa [ ] 3 2 5 3 1.8110 m 7.75 10 m
9
单辉祖:材料力学教程
例10-2 图中所示结构,承受载荷F=12kN作用。横梁AC用 No14工字钢制成,许用应力[σ]=160MPa,试校核其强度。
2 2 M T r3 [ ] W
2 2 r4 M 3 T [ ]
2 2 M 0 . 75 T r4 [ ] W 单辉祖:材料力学教程
14
弯拉(压)扭组合强度计算
弯拉扭组合 危险截面-截面A 危 险 点- a
a M N M
材料力学第10章 组合变形

因此,截面O为危险截面。
危险截面上,由轴力引起的正应力均匀分布,其值
为
,由弯矩引起的正应力线性分布,其值为
。利用叠加原理,将拉伸及弯曲正应力叠加
后,危险截面上正应力沿截面高度的变化情况如图10.5
(e)所示,仍为线性分布。而且可以看出,最大拉应
力和最大压应力分别发生在O截面上、下边缘各点,其
值为
(10.4)
图10.5
依据上述分析,弯拉(压)组合变形时危险点处于单向应力状态,所以可将 截面上的σmax与材料的许用应力相比较建立其强度条件。对于拉压强度相等 的材料,强度条件为
对于抗拉与抗压性能不同的材料,强度条件为
下面举例说明弯拉(压)组合变形的强度计算。 例10.2如图10.6(a)所示的钢支架,已知载荷F=45 kN,尺寸如图。 (1)如材料为钢材,许用应力[σ]=160 MPa,试选择AC杆的工字钢型号。 (2)如材料为铸铁,许用拉应力[σt]=30 MPa,许用压应力[σc]=160 MPa,且AC杆截面形式和尺寸如图10.6(e)所示,A=15×10-3 m2,z0=75mm ,Iy=5.31×10-5 m4。试校核AC杆的强度。
其力矩矢量分别与y轴和z轴的正向一致(见图10.2(b))。 为了确定横截面上最大正应力点的位置,先求截面中性轴位置。记中性轴上 任一点的坐标为(y0,z0),由于中性轴上各点处的正应力均为零,所以由式 可得中性轴方程为
(10.2) 可见,中性轴是一条通过横截面形心的直线(见图10.2(c)),其与y轴的 夹角θ为
图10.3 例10.1如图10.4(a)所示,20a号工字钢悬臂梁承受均布载荷q和集中力
。已知钢的许用弯曲正应力[σ]=160 MPa,a=1 m。试求梁的许可 载荷集度[q]。 解由于梁所受到的横向力不在梁的两个纵向对称面内,此时可以将横向力向 两个纵向对称面分解(向y和z轴分解),从而将其看成是梁在其两个相互垂
第十章-组合变形
= 1.064kN ⋅ m
0.227kN.m 1kN.m Mz 图 0.364kN.m
2 2 M C = M yC + M zC
My 图 0.568kN.m
_
= 0.227 + 0.568 = 0.612kN ⋅ m
2
2
B截面为危险截面。 截面为危险截面。 截面为危险截面
T 图 1kN..m
3)校核强度
2
=
M +T Wz
2
M r3 = Wz
2
σ r4 =
M + 0.75T Wz
2
M r4 = Wz
σ r3 =
M +T Wz
2
2
σ r4 =
M + 0.75T Wz
2
2
第三、 第三、第四强度理论的第三种表达形式
M r3 = M + T
2
2
M r 4 = M + 0.75T
2
2
第三、第四强度理论的相当弯矩 第三、 使用条件: 使用条件: 符合第二种表达形式的使用条件, 1. 符合第二种表达形式的使用条件, 圆截面杆, 2. 圆截面杆, 正应力主要由弯矩产生, 3. 正应力主要由弯矩产生, 切应力主要由扭矩产生。 4. 切应力主要由扭矩产生。
偏心拉伸(压缩) 二、偏心拉伸(压缩)
F z (yF,zF) y F z y My My=FzF F Mz My Mz=FyF z y
1. 应力计算:对载荷进行等效平移、分组和叠加。 应力计算:对载荷进行等效平移、分组和叠加。
P z y My z y Mz z y
σ=
FN M y z0 M z y0 ± ± Iz Iy A
材料力学10组合变形

10 组合变形110 组合变形10.1 斜弯曲10.2 拉伸(压缩)与弯曲组合变形10.3 弯曲与扭转组合变形10.4 偏心拉伸与压缩10.5 截面核心23轴向拉压M eM e扭转○○○F平面弯曲一、基本变形回顾FF4轴向拉压AF N=σFFFF NFσ5扭转PI M T ρτ=Pm axW M T =τM eM eM eM TM Tτmaxτmaxρτ6平面弯曲z z I y M =σ中性层xyz主轴平面xyσ(M z )中性轴zzW M ±=m in m ax σσF Qy M z7zx yσ(M y )中性轴平面弯曲yy I z M =σyy W M ±=m in m axσσ中性层xyz主轴平面xzF Qz M yyxz8事实上,基本变形不过是简化模型,只有在一种变形特别突出,其余变形可以忽略不计的情况下才有可能发生。
FF q <<FFF当几种基本变形的影响相近时再用简单模型计算,将会引起较大的误差。
二、组合变形结构上同时发生两种或两种以上的基本变形。
F檩条斜弯曲:两平面弯曲的组合910压弯组合变形ABF AxF AyPF F xF y压弯组合变形1112偏心压缩拉弯组合变形1314q弯扭组合变形15弯扭组合变形F双向弯曲与扭转组合变形16组合变形的形式有很多种,本章学习四种典型形式。
1. 斜弯曲;2. 拉伸(压缩)与弯曲组合;3. 弯曲与扭转组合;4. 偏心拉伸与压缩。
应注意通过这四种典型组合变形的学习,学会一般组合变形的计算原理和方法。
1718三、组合变形下的计算⑤用强度理论进行强度计算。
基本解法:①外力分解或简化:使每一组力只产生一个方向的一种基本变形;②分别计算各基本变形下的内力及应力;④对危险点进行应力分析;分析方法:叠加法前提条件:小变形思考题1. 分析组合变形时,先分后合的依据是什么?2.叠加原理的适用条件是什么?能否应用于大变形情况?1920平面弯曲斜弯曲:两个相互垂直平面内平面弯曲的组合一、斜弯曲的特征10.1 斜弯曲21受力特征:外力作用线通过截面的弯曲中心,但不与任一形心主轴重合或平行;变形特征:变形后的挠曲线不与外力作用面相重合或平行。
材料力学10组合变形PPT课件

0McIozsy0sIiynz0
中性轴方程
cos
Iz y0
sIiynz0
0
( y0,z0 )
z
α φ
(1)中性轴是一条过截面形心 F 的直线;
y 中性轴
斜率 tany0 Iz tan
29
z0 Iy
10.1 斜弯曲
tan Iz tan
Iy
(2) 当Iz≠Iy,α ≠ φ,中性
轴与荷载线不垂直。
z
F
17
三、组合变形下的计算
分析方法:叠加法 前提条件:小变形
基本解法:
①外力分解或简化:使每一组力只产生一个方向的一种 基本变形; ②分别计算各基本变形下的内力及应力;
④对危险点进行应力分析; ⑤用强度理论进行强度计算。
18
思考题
1. 分析组合变形时,先分后合的依据是什么? 2.叠加原理的适用条件是什么? 能否应用于 大变形情况?
F
Fy
Fx B P
压弯组合变形
10
压弯组合变形
11
12
偏心压缩
拉弯组合变形
13
q
弯扭组合变形
14
F
弯扭组合变形
15
双向弯曲与扭转组合变形
16
组合变形的形式有很多种,本章学习四种典型形式。 1. 斜弯曲; 2. 拉伸(压缩)与弯曲组合; 3. 弯曲与扭转组合; 4. 偏心拉伸与压缩。
应注意通过这四种典型组合变形的学习,学会一般 组合变形的计算原理和方法。
A
B
C
22
10.1 斜弯曲
二、斜弯曲的研究方法
1.分解 将外力沿横截面的两个形心主轴分解,得到两个正 交的平面弯曲。
材料力学第十章 组合变形

r 3 2 4 2
r3
2 M y M z2 T 2
W
M 2 T 2 W
r 4 3
2
2
2 M y M z2 0.75T 2
r4
W
M 2 0.75T 2 W
例3 图示空心圆杆,
内径d=24mm,外
径D=30mm, P1=600N, []=100MPa,试用 第三强度理论校核 A
Lmax D1
⑤变形计算
ymax D 2
f f
2 y 2 z
fz
f
tg
fy fz
f fy
当j = 时,即为平面弯曲。
例1结构如图,P过形心且与z轴成j角,求此梁的最大应力与挠度。 解:危险点分析如图 中性轴 h Pz
x
Py
P z j z
D2 P 变形计算 Py y
P
P
10203 [ 1020252 ] 12 7.27105 mm4
M 5P 3 500Nm 10
P N M
20 20
y yC z
应力分析如图
100
N M z max max A I yc
P
100 103 500 55 103 6 800 10 7.27107
P Mz y Myz x A Iz Iy
三、中性轴方程
P M z y0 M y z0 x 0 A Iz Iy
对于偏心拉压问题 P Py y Pz z P yP y0 z P z0 P 0 P 0 (1 2 2 )0 y 2 2 A Aiz Aiy A iz iy y
1
材料力学 第十章 组合变形(4,5,6)
[例10-7]:偏心拉伸杆,弹 性模量为E,尺寸、受力如图 所示。求: (1)最大拉应力和最大压 应力的位置和数值; (2)AB长度的改变量。 分析:这是偏心拉伸问题
最大拉应力发生在AB线 上各点,最大压应力发 生在CD线上各点。
CL11TU24
解:(1)应力分析
Ph Pb N P, M y , M z 2 2 t N M y Mz c A Wy Wz
3.算例 [例10-4]求高h,宽b的矩形截面的截面核。 b (1)作中性轴Ⅰ,z , a y a 解:
(2)求载荷点① , 2 iy b2 2 b zF ② az 2 6 b 3 z iz ③ yF 0 ① ay ④ (3)作中性轴Ⅱ , h a z , a y 2 b y b (4)求载荷点② , 2 2 2 Ⅰ 2 2 iy iz h h h z F 0, yF ay 6 2 3 az
(1)过截面周边上的一点作切线,以此作为第一 根中性轴; (2)据第一根中性轴的截距求第一个载荷点坐标; (3)过截面周边上相邻的另一点作切线,以此作 为第二根中性轴; (4)按(2)求于第二个中性轴对应的第二个载荷 点坐标; (5)按以上步骤求于切于周边的各特征中性轴对应 的若干个载荷点,依次连接成封闭曲线即截面核心。
中性轴把横截面分为受拉区和受压区,两个 区范围的大小受载荷作用点坐标的控制。 定义:使横截面仅受一种性质的力时载荷作用 的最大范围成为截面核心。
二.截面核心的求法 1.截距与载荷坐标的关系
z F , az ; zF , az
2.作截面核心的方法
zF 0, az ; zF , az 0
解:(1)简化外力:
材料力学 第十章组合变形(123)PPT课件
18
例题 8-1
解:1. 将集中荷载F 沿梁横截面的两个对称轴y、z分解为
F y F c4 o o 0 s q 2 ca 4 o o 0 s 0 .3q 8 a 3
F z F s4 io n 0 q 2sa 4 io n 0 0 .3q 2 a 1
19
例题 8-1
2. 梁的计算简图如图b所示,并分别作水平弯曲和 竖直弯曲的弯矩My图和Mz 图(图c ,d)。
纵向对称面:梁的轴线与横截面纵向对称轴所构成的平面
平面弯曲:当作用在梁上的载荷和支反力均
位于纵向对称面内时,梁的轴线由直线弯成
一条位于纵向对称面内的曲线。 F'
F'
F
F'
纵向对称面?
轴线
7
CL7TU1
一.定义:斜弯曲—荷载不作用在构件的纵向对称 面内,梁的轴线变形后不在位于外力所在平面内。
一.力的分解
Fy Fcos
Fz Fsin
z
C
(y, z)
Fz
Fy
Fy
8
CL11TU3
Mz Fy(l x)以z为中性轴弯曲
My Fz(l x)以y为中性轴弯曲
Mz Fcos(lx)Mcos My Fsin(lx)Msin
二.基本变形分析
1.应力计算
z
M
的应力
z
Mz yMycos
Iz
Iz
y
9
M
的应力
y
Myz Mzsin
21
例题 8-1 z
(e)
MyA
z
D1 z
MzA
D2
y
yyBiblioteka (m )A a x M W y y A M W z zA 0 3 .6 .5 q 1 4 1 (1 6 2 2 0 ) 0 .2 2 q 3 6 1 ( 1 6 7 2 6 0 ) (2.1 5130)q
材料力学第10章 组合变形综述资料.
当力和弯矩作用在一个非对称平面上,杆件弯曲方向?
2020/7/3
F F
F F
16
材料力学-第10章 组合变形
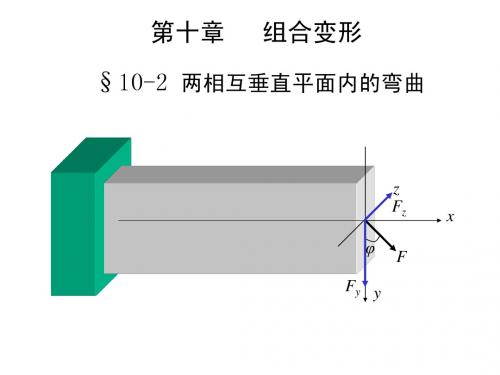
两相互垂直平面内的弯曲
矩形截面分析:
中性轴
Mz z
My
M
z
θ
M
y
y
如果弯曲平面和弯矩作用平面一致,那么必须
2020/7/3
17
材料力学-第10章 组合变形
14
材料力学-第10章 组合变形
两相互垂直平面内的弯曲
对于圆形截面,杆的变形与弯矩作用平面在同一平面内
A
A
F
F
F
w
w
弯曲平面在哪 个方向?
对于矩形截面,变形与弯矩作用平面是否仍在同一 平面?
2020/7/3
15
材料力学-第10章 组合变形
两相互垂直平面内的弯曲
圆形截面:任何通过轴心的力引起的弯矩所作用的平面均为 截面的对称面
2020/7/3
10
叠加原理
材料力学-第10章 组合变形
基本方法
变形
线弹性、小变形
分解
基本变形1 基本变形2 基本变形n
叠加
组合变形
2020/7/3
11
2020/7/3
材料力学-第10章 组合变形
计算简图
借助于带轮或齿轮传递功率 的传动轴,工作时在齿轮的齿上 均有外力作用。
将作用在齿轮上的力向轴的 截面形心简化便得到与之等效的 力和力偶,这表明轴将承受横向 载荷和扭转载荷。
矩形截面应力分析:
矩形截面内任一点的弯曲正应力
Mz z
My
Mz
[理学]材料力学第10章_OK
max
F M y zmax
A
Iy
M z ymax Iz
24
若材料的许用拉应力[σt]和许用压应力[σc]不相等时,则须
分别对最大拉应力和最大压应力做强度计算。
t max
F A
限的各点产生拉应力时取正值,产生压应力时取负值。还
可以根据杆件的变形情况来确定。例如图9.7b中确定G点 的应力时,在My作用下G处于受压区,则式中第二项取负 值,在Mz作用下G处于受拉区,则式中第三项取正值。
在F、My、Mz各自单独作用下,横截面上应力的分布情
况如图9.10a、b、c所示。图9.10d为三者共同作用下横截面 上的应力分布情况。
M y z M sin z
Iy
Iy
M
co s
Iz
y sin
Iy
z
M和y、z可均取绝对值,应力的正负号根据梁的变形来直接判断。
8
3、 中性轴方程
为确定截面上最大正应力点的位置,先确定中性轴
的方程:设x0、y0为中性轴上任一点的坐标,由中性轴
各点处的正应力均为零,得中性轴方程为:
力发生在铅垂直径
的上、下两端点C1
29
和C2处。
危险截面上弯曲正应力在与中性轴C3C4垂直方向的变化 如图e,扭转切应力沿直径C3C4和C1C2的变化如图f。
其中正应力和切应力值为
M W
Fl πd 3 / 32
T
Wp
T 2W
Fa πd 3 /16
30
对于许用拉、压应力相等的塑性材料制成的杆,这两 点的危险程度是相同的。为此,取其中的点C1来研究。 C点的应力状态如图(g)所示。可见C点处于平面应力 状态,其三个主应力为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
弯压组合
可见,危险截面为C截面 其轴力和弯矩分别为
FNC 3 kN M c M max 4 2 8kN m
A
FAy
10kN m a x
g g f
C m
FBy
B
危险点 截面C上的最低点f 和最高点g
FN M c s A W
f
18
弯压组合
A I
4
10kN
解 首先计算折杆的支座反力 由平衡方程可得 FAx A
FAx 0, FAy 5kN, FBy 5kN
FAy
m
10kN
C 1.2m B 1.6m FBy
a x 1.6m
m
由于折杆左右对称,所以只需分析一半即可。 折杆AC部分任一截面上的内力
FN FAy sin 3 kN FS FAy cos 4 kN M xFAy cos
杆件变形分析步骤 首先, 在杆件原始尺寸上分别计算由横向力和 轴向力引起变形、应力 然后, 利用叠加原理,合成在横向力和轴向力 共同作用下杆件变形、应变和应力等物理量 若杆件抗弯刚度EI较大,轴力引起杆件的弯曲 变形较小,可以忽略
10
弯拉组合
细长杆件强度问题, 受力如图,抗弯刚度 EI,截面抗弯模量W , 横截面面积A。
n
e n
P
z b h y
30
偏心拉伸(压缩)
解: 1. 力系简化 力P对竖直杆作用等效于作 用在杆轴线上一对轴力P和 一对作用在竖直平面内力 偶mz=Pe
FN P 2000 N, M z mz Pe 120 N m
mz P
n
e n
P
mz P
可见,竖直杆发生弯拉组合变形
31
偏心拉伸(压缩)
1 Iz 0.93 0.4 0.43 0.6 12 27.5 10 3 m 4
F 0.6 D 0.4 C E o
z 0.2 0.2 G 单位:m H A y
0.45
0.45
B
iy
2
Iy
A Iz 2 iz 4.58 10 2 m 2 A 38
8 10 2 m 2
19
f
偏心拉伸(压缩)
x
o
P z y A(yp, zp)
20
偏心拉伸(压缩)
概念 当杆件上外力作用线与杆件轴线平行但不 重合时,将引起杆件偏心拉伸(压缩)
设杆件横截面有两个对称轴, 且在杆件一端的横截面上作 用有偏心拉力P,作用点为 A(yp , zp)。 下面分析杆件的变形
x
o
P
z y A ( y p, z p)
内力分析---基本变形
FN Fs M 忽略轴力对弯曲变形影响 轴力FN引起轴向变形 忽略剪力Fs对弯曲变形贡献 弯矩M引起弯曲变形
11
A
P C a b
B F
弯拉组合
内力图---危险截面
FN=F
Pb ,0 x a ab FS Pa , a x l ab
2
2 iy iz a y , az yp zp
2
az1
z
C1 ay1
y
A1(yp1, zp1)
iy
2
得外力作用点坐标A1(yp1, zp1)
y p1
iz , z p1 a y1 a z1
36
2
iy
2
偏心拉伸(压缩)
以此类推, 选取截面边界上的一点C2,得 外力作用点的坐标A2(yp2, zp2) 选取截面边界上的一点C3,得 外力作用点的坐标A3(yp3, zp3) ……. 选取截面边界上的一点Cn,得 外力作用点的坐标An(ypn, zpn)
24
偏心拉伸(压缩)
根据叠加原理,横截面上 点(x, y, z)处正应力为
s s s s
Py p P Pz p z y A Iy Iz
x
my
P o
mz
z
y A(yp, zp)
根据惯性矩和惯性半径关系,有
I y A i y , I z A iz
偏心拉伸(压缩)
对边界切线① ,其坐标轴截距为 从而,外力作用点P1的坐标 2
a y 0.45, az
z
2 iy iz y p 0.102, z p 0 ay az
F
G
④
③
D E
同理,对边界切线② ,外力作用 点P2的坐标为(0, 0.2) 对边界切线③ ,外力作用点P3的 坐标为(0.102, 0) 对边界切线④ ,外力作用点P4的 坐标为(0, −0.133)
A
P C a e d z c y b
B F
sN
sM
s N s M
f
横截面一点的应力公式
FN M s ( y, z ) y A Iz
危险点:C截面ed和c计
A
P C a b
B F
plastic : brittle :
s max
FN M max [s ] A Wz
第十章 组合变形
主 讲人: 张能辉
1
组合变形概念
杆件基本变形
杆件的自由扭转变形
杆件的轴向拉伸(压缩)变形
杆件的平面弯曲变形
2
组合变形概念
工程实际中,构件在外载荷的作用下, 经常发生两种或两种以上的基本变形 组合变形——杆件除基本变形(拉伸、 压缩、平面弯曲和自由扭转)以外的其 它变形形式称为组合变形
z yp P s 1 p z 2 2 A i i y z P x z
o
y
y A(yp, zp)
z o ay az y
中性轴
34
偏心拉伸(压缩)
当外力作用点位于截面形心附近 的某个区域时,中性轴不穿过横 截面,这个区域被称为截面核心。 当外力作用在截面核心边界上时, 中性轴恰好与截面边界相切。 可利用该关系确定截面核心位置
my
P o
mz
z
y A(yp, zp)
23
偏心拉伸(压缩)
2. 应力分析
轴向力P作用下, 横截面上正应力为
P s A
x
my
P o
mz
z
A(ypy , zp)
在弯矩My=zp P, Mz=yp P作用下, 横截面上正应力为
s
my Iy z Pz p Iy z
Py p Mz s y y Iz Iz
26
偏心拉伸(压缩)
中性轴与坐标轴oy和oz交点为
iy iz a y , az yp zp
2 2
1
zp iy
2
z0
yp iz
2
y0 0
z D1 o D2 ay az y
中性轴
可见,中性轴是一条不通过形心的直线,且中性轴 与偏心力作用点分别处于截面形心的相对两侧。 确定中性轴后,横截面上距中性轴最远的两点D1 和D2分别为拉应力和压应力最大值点(危险点)。
C2 az1 An A1 C3 z C1 A3 A2 Cn y ay1
连接点C1,C2,C3,,Cn,得一条封闭曲线, 该曲线就是截面核心的边界。 曲线所围成的区域为截面核心。
37
偏心拉伸(压缩)
已知y、z两轴为截面形心 主惯性轴。试确定图示T字 形截面的截面核心。
解 横截面几何性质
A 0.9 0.4 0.4 0.6 0.6 m2 1 I y 0.9 0.43 0.4 0.63 3 48 10 3 m 4
s t max [s t ]
s c max [s c ]
14
弯压组合
15
弯压组合
10kN C 1.2m B 1.6m 1.6m
A
折杆由两根无缝钢管焊接而成,已知两 根钢管直径均为140mm,壁厚为10mm, 其它几何尺寸和受力情况如图,求折杆 危险截面上的最大正应力和最小正应力。
16
弯压组合
P
z y
My=zp P
z y
Mz=yp P
z y z y
+
+
=
中性轴
轴向拉伸
绕oy轴弯曲
绕oz轴弯曲
偏心拉伸
29
偏心拉伸(压缩)
夹具夹零件时受到外力作用 已知外力P=2kN, 作用线与夹 具竖杆轴线间距离 e=60mm, 竖直杆横截面尺寸b=10mm, h=22mm, 材料许用应力[s ]=170MPa 校核竖直杆的强度
3
组合变形概念
工程实例
示意图
受力图
=
平面弯曲
+
轴向压缩
4
组合变形概念
=
+
受力图
轴向压缩
平面弯曲
5
组合变形概念
受力图
扭转变形
弯曲变形
=
+ +
弯曲变形
6
组合变形概念
在构件的组合变形中
如果材料在线弹性、小变形范围内,可先将外 载荷简化为几组符合基本变形外力作用条件的 外力系,在原始尺寸上分别计算构件在每一种 基本变形形式下的内力、应力和变形。然后利 用叠加原理,综合考虑各基本变形,以确定构 件的总内力、应力和变形,从而确定构件的危 险截面、危险点,进行强度计算
( D 2 d 2 ) 40.8 10 4 m 2 , ( D d ) 868 10 m
4 4 8 4
m A a x
g f
C m B
FBy
64 I W 124 10 6 m 3
D 2
FAy
