第十章_logit回归
logistic回归分析精选PPT课件
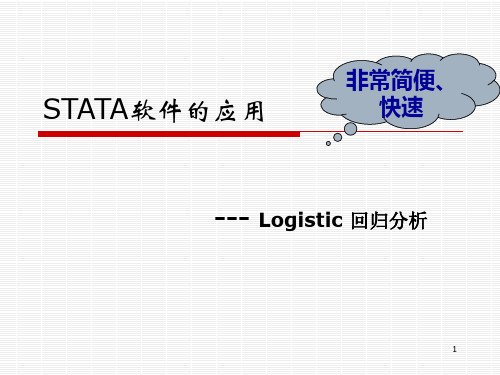
Number of obs =
LR chi2(1)
=
Prob > chi2
=
Pseudo R2
=
152 30.67 0.0000 0.1455
------------------------------------------------------------------------------
case |
Coef. Std. Err.
z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
exposure | 2.112829 .4228578 5.00 0.000 1.284043 2.941615
2
二分类资料的分析
非条件logistic模型:成组病例对照研究资料 条件logistic模型:配比病例对照研究资料3源自非条件logistic回归模型
lo ( p ) g 0 + i 1 X 1 + t = 2 X 2 k X k
01X1+ 2X2+ + kXk
p1ee01X12X2 kXk 1
|------------------------+----------------------
Odds ratio |
8.271605
| 3.4193 21.33091 (exact)
Attr. frac. ex. |
.8791045
| .7075425 .9531197 (exact)
Attr. frac. pop |
.4626866
《Logistic回归》课件

公式
f(x)=1/(1+e^-x)其中,x是一个实数,源自表示 自然对数的底数。特点
• 输出范围在0-1之间,代 表了一个概率值;
• 函数有单峰性,中心对 称,可以确定最大值和
• 最在小输值入;接近0时函数近 似于线性函数。
应用场景:二元Logistic回归
乳腺癌预测
贷款审核
二元Logistic回归被广泛应用于医 学界用于识别患有乳腺癌的女性。
数据预处理
4
的潜在关系和规律。
对需要进行缩放、归一化、标准化等处
理的变量进行预处理。
5
模型拟合
将数据划分训练集和测试集,通过模型 对训练集进行拟合,并评估模型预测能 力。
模型评估方法
混淆矩阵
将预测结果与真实结果进行比对,计算假正率、假负率、真正率和真负率等指标。
ROC曲线
通过绘制真正率与假正率的曲线,评估模型的预测能力。
AUC指标
ROC曲线下的面积就是AUC,AUC越大说明模型预测结果越准确。
常见模型优化方法
1 数据增强
通过合成数据或者样本扩 增等方法,增加数据量, 提高模型泛化性能。
2 特征选择
选择对于问题最重要的变 量,避免过拟合。
3 模型集成
通过结合多个模型的结果, 提高整体预测能力。
应用探索:Logistic回归的扩展
2 作用
通过逻辑函数将线性变量转化为概率值,从 而进行二元分类。
3 优点
简单易懂、易于解释和使用,对于大规模数 据集有效率。
4 缺点
只适用于二元分类问题,并且在分类较为复 杂的非线性问题上表现较差。
sigmoid函数
介绍
sigmoid函数是Logistic回归模 型中核心的激活函数,将输入 值映射到0-1的概率分布区间内。
10_第十讲_Logistic回归1228

0.12
0.13
0.88
0.87
-1.99243
-1.90096
• 以结果变量为二分类变量为例:
– P/(1-P)为比数,定义Y=ln(P/(1-P))
• 其基本思路与多元线性回归分析相同。
– 将应变量由二分类变量转为连续性变量; – 确定m个自变量 (研究因素与混杂因素)。
Logistic模型的构建
(二)Logistic回归的应用条件
• 样本含量足够,一般为自变量个数的5-10倍; • 结果变量满足独立性,常为二分类变量资料, 自变量可以是数值变量/分类变量或等级资料; • 分析前需将分类变量资料与等级资料定量化。
(三)Logistic回归的用途
• 可以在控制1个或多个混杂因素的条件下,探 讨某个事件的发生与研究因素的关系;研究 各因素主效应及其相互间的交互作用; • 在临床研究中多用于鉴别诊断、评价疗效、 分析与疾病预后有关的因素、筛选主要危险 因素、预测不良事件发生。
冠心 病 Total
control case
P=0.029
• 吸烟:
冠 心病 * 吸 烟 C r o s s t a b u l a t i o n Count 吸烟 N 冠心 病 Total control case 10 3 13 Y 18 23 41 Total 28 26 54
P=0.038
0.99 0.98 0.97 0.96
-4.59512 -3.89182 -3.4761 -3.17805
0.05
0.06 0.07
0.95
0.94 0.93
-2.94444
-2.75154 -2.58669
0.08
0.09 0.1 0.11
Logistic回归分析PPT课件

汕大医学院预防医学教研室
1
第一节 Logistic 回归
Logistic regression:
是研究分类变量统计分析的一种重要方 法。研究两水平或多水平反应变量与其影 响因子间关系的回归分析(线性回归分析: 应变量为连续计量资料)。 Logistic回归模型是一种概率模型, 通常以疾 病,死亡等结果发生的概率为因变量, 影响疾 病发生的因素为自变量建立回归模型。
19
• Logistic回归中的常数项(b0)表示,在不接触任 何潜在危险/保护因素条件下,效应指标发生与 不发生事件的概率之比的对数值。
• Logistic回归中的回归系数( bi )表示,某一因 素改变一个单位时,效应指标发生与不发生事件 的概率之比的对数变化值,即OR的对数值。
20
Logistic回归系数的意义
11
• (1)取值问题 • (2)曲线关联 • 反应变量与自变量的关系通常不是直线关
系,而是S型曲线。曲线回归时,往往采用 变量变换,使得曲线直线化,再进行直线 回归方程的拟合。能否考虑对所预测的因 变量加以变换。1970年,COX引入了用于 人口学领域的Logit变换。
12
概率P是以0.5为对称点,分布在0~1的范围内 的,而相应的Logit(P)的大小为
4
实例
试验者术前检查了53例前列腺癌患者,拟 用年龄(AGE)、酸性磷酸酯酶(ACID)两个连 续型的变量,X射线(X-RAY)、术前探针活 检病理分级(GRADE)、直肠指检肿瘤的大小 与位置(STAGE)三个分类变量与手术探查结 果变量NODES(1、0分别表示癌症的淋巴结 转移与未转移 )建立淋巴结转移的预报模 型。
5
53例接受手术的前列腺癌患者情况
第10讲 第10章 Logistic回归

Odds 1 机会比率 Odds 2
若消费支出2000元且有卡 (X1=2,X2=1),则
P (Y 1 | X 1 2, X 2 1) Odds1 1 P (Y 1 | X 1 2, X 2 1)
若消费支出2000元且无卡 (X1=2,X2=0),则
P (Y 1 | X 1 2, X 2 0) Odds2 1 P (Y 1 | X 1 2, X 2 0)
利用机会比率与回归系数之间的关系就容易计算机 会比率的估计值
SPSS 分析结果中的估计机会
Va riable s in the E quation St ep a 1 信用卡 年消费 Co nstant B 1.099 .342 -2.146 S. E. .445 .129 .577 Wald 6.105 7.050 13.82 6 df 1 1 1 Si g. .013 .008 .000 Exp(B ) 3.000 1.407 .117
exp( 2.1464 0.3416X 1 1.098X 2 ) ˆ y 1 exp( 2.1464 0.3416X 1 1.098X 2 )
例如估计去年消费支出为2000元而没有信用卡的顾 客购买商品的概率,此时X1=2,X2=0,代入上式
exp( 2.1464 0.3416 2 1.098 0) p 1 exp( 2.1464 0.3416 2 1.098 0)
已知 X1=2,X2=1,P(Y=1)=0.4099. 已知 X1=2,X2=0,P(Y=1)=0.1880.
0.4099 Odds 1 0.6946 1 0.4099 0.1880 Odds 2 0.2315 1 0.1880
Odds 1 0.6946 机会比率 3.00 Odds 2 0.2315
第十章:离散状态变量的回归

• (3)一只球队的成绩
1,胜 Y=
2,负 3,平
二、因变量是离散状态的回归
• 2、离散状态因变量回归方程的意义 (两状态的情况)
Di 0 1X i i
能否进行 这样的回
归呢?
Di 0 或 1
二、因变量是离散状态的回归
• 2、离散状态因变量回归方程的意义 (两状态的情况)
Di的期望值:
所以,应该采用“可行的广义最小二 乘法”,而不是“普通最小二乘法”
二、因变量是离散状态的回归
• 3、离散状态因变量回归遇到的障碍 (2)异方差
步骤: A. 使用OLS进行估计,并得到拟合值 Dˆi
B. 在原方程左右同时除以 Dˆi(1 Dˆi )
之后,再进行OLS估计;
二、因变量是离散状态的回归
二、因变量是离散状态的回归
• 3、离散状态因变量回归遇到的障碍
答案:可以,但有问题!
二、因变量是离散状态的回归
• 3、离散状态因变量回归遇到的障碍 (1)误差非正态分布
i Di (0 1X i ) 其中,Di是1或0的随机变量;
而X是非随机的,或者虽然是随机的,但不 一定是正态的。
即使X是随机的且是正态的,εi也不会是正 态的。
在线性回归与二值结果之间,引入 一个连续取值的潜变量(latent variable)
例如,在前例中,引入一个“实力” 潜变量,Z。
二、因变量是离散状态的回归
• 4、解决方法
“让球数”直接的与“实力”相关联, 而“实力”与“结果”相关联。
Z 0 1X i i
Z 0时,D ( 1 获胜);注值意不:一阀定 Z 0时,D ( 0 输); 为0!
What Point Spreads Say About the Probability of Winning in the NFL: I
第十章_logit回归

第十章 logitic 回归本章导读:Logitic 回归模型是离散选择模型之一,属于多重变数分析范畴,是社会学、生物统计学、临床、数量心理学、市场营销、会计与财务等实证分析的常用方法。
10.1 logit 模型和原理Logistic 回归分析是对因变量为定性变量的回归分析。
它是一种非线性模型。
其基本特点是:因变量必须是二分类变量,若令因变量为y ,则常用y=1表示“yes ”,y=0表示“no ”。
[在发放股利与不发放股利的研究中,分别表示发放和不发放股利的公司]。
自变量可以为虚拟变量也可以为连续变量。
从模型的角度出发,不妨把事件发生的情况定义为y=1,事件未发生的情况定义为0,这样取值为0、1的因变量可以写作:⎩⎨⎧===事情未发生事情发生01y 我们可以采用多种方法对取值为0、1的因变量进行分析。
通常以P 表示事件发生的概率(事件未发生的概率为1-P ),并把P 看作自变量x 的线性函数。
由于y 是0-1型Bernoulli 分布,因此有如下分布:P=P (y=1|x ):自变量为x 时y=1的概率,即发放现金股利公司的概率1-P=P (y=0|x ):自变量为x 时y=0的概率,即不发放现金股利公司的概率 事件发生和不发生的概率比成为发生比,即相对风险,表现为PP odds -=1.因为是以 对数形式出现的,故该发生比为对数发生比(log odds ),表现为)1ln(P P odds -=。
对数发生比也是事件发生概率P 的一个特定函数,通过logistic 转换,该函数可以写成logistic 回归的logit 模型:)1(log )(log PP P it e -= Logit 一方面表达出它是事件发生概率P 的转换单位;另一方面,它作为回归的因变量就可以自己与自变量之间的依存关系保持传统回归模式。
根据离散型随即变量期望值的定义,可得:E(y)=1(P)+0(1-P)=P进而得到x P y E 10)(ββ+==因此,从以上分析可以看出,当因变量的取值为0、1时,均值x y E 10)(ββ+=总是代表给定自变量时y=1的概率。
Logistic回归2

第十章 Logistic 回归分析第一节 Logistic 回归基本概念线性回归模型的一个局限性是要求因变量是定量变量(定距变量、定比变量)而不能是定性变量(定序变量、定类变量)。
但是在许多实际问题中,经常出现因变量是定性变量(分类变量)的情况。
可用于处理分类因变量的统计分析方法有:判别分别(Discriminant analysis)、Probit 分析、Logistic 回归分析和对数线性模型等。
在社会科学中,应用最多的是Logistic 回归分析。
Logistic 回归分析根据因变量取值类别不同,又可以分为Binary Logistic 回归分析和Multinomial Logistic 回归分析,Binary Logistic 回归模型中因变量只能取两个值1 和0(虚拟因变量),而Multinomial Logistic 回归模型中因变量可以取多个值。
本章将只讨论Binary Logistic 回归,并简称Logistic 回归。
因变量只取两个值,表示一种决策、一种结果的两种可能性。
从模型角度出发,不妨把事件发生的情况定义为Y=1,事件未发生的情况定义为Y=0,这样取值为0、1 的因变量可以写为下式:10y ⎧=⎨⎩ 事件发生 事件未发生我们可以采用多种方法对取值为0、1 的因变量进行分析。
通常以p 表示事件发生的概率(事件未发生的概率为1-p ),并把p 看作自变量X i 的线性函数,即p = P ( y = 1) = F (i i X β) i = 1,2,… , k不同形式的F(·),就有不同形式的模型,最简单的莫过于使F(·)为一线性函数,即01122k k =+++++p X X X ββββε (10-113)我们可能会认为可用普通最小二乘法对上式进行估计,但因p 的值一定在区间[0,1]内,而且当p 接近于0或1时,自变量即使有很大变化p 的值也不可能变化很大,所以对上式直接用普通最小二乘法进行估计是行不通的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十章 logitic 回归本章导读:Logitic 回归模型是离散选择模型之一,属于多重变数分析范畴,是社会学、生物统计学、临床、数量心理学、市场营销、会计与财务等实证分析的常用方法。
10.1 logit 模型和原理Logistic 回归分析是对因变量为定性变量的回归分析。
它是一种非线性模型。
其基本特点是:因变量必须是二分类变量,若令因变量为y ,则常用y=1表示“yes ”,y=0表示“no ”。
[在发放股利与不发放股利的研究中,分别表示发放和不发放股利的公司]。
自变量可以为虚拟变量也可以为连续变量。
从模型的角度出发,不妨把事件发生的情况定义为y=1,事件未发生的情况定义为0,这样取值为0、1的因变量可以写作:⎩⎨⎧===事情未发生事情发生01y 我们可以采用多种方法对取值为0、1的因变量进行分析。
通常以P 表示事件发生的概率(事件未发生的概率为1-P ),并把P 看作自变量x 的线性函数。
由于y 是0-1型Bernoulli 分布,因此有如下分布:P=P (y=1|x ):自变量为x 时y=1的概率,即发放现金股利公司的概率1-P=P (y=0|x ):自变量为x 时y=0的概率,即不发放现金股利公司的概率 事件发生和不发生的概率比成为发生比,即相对风险,表现为PP odds -=1.因为是以 对数形式出现的,故该发生比为对数发生比(log odds ),表现为)1ln(P P odds -=。
对数发生比也是事件发生概率P 的一个特定函数,通过logistic 转换,该函数可以写成logistic 回归的logit 模型:)1(log )(log PP P it e -= Logit 一方面表达出它是事件发生概率P 的转换单位;另一方面,它作为回归的因变量就可以自己与自变量之间的依存关系保持传统回归模式。
根据离散型随即变量期望值的定义,可得:E(y)=1(P)+0(1-P)=P进而得到x P y E 10)(ββ+==因此,从以上分析可以看出,当因变量的取值为0、1时,均值x y E 10)(ββ+=总是代表给定自变量时y=1的概率。
虽然这是从简单线性回归分析而得,但也适合复杂的多元回归函数情况。
k k x x x itP y E ββββ++++==Λ22110log )(β0为常数项,β1,β2,…,βk 分别为k 个自变量的回归系数。
因此,logistic 模型为:kk k k x x x x x x P P e e e e P f ββββββββ+++++++++=+=ΛΛ221102211011)(10.2 模型的stata 程序Stata 有两个命令可进行二元logistic 回归分析:logit 和logistic 。
其分析的结果的实质是一样的。
但输出的结果的表现形式有所不同。
前者提供参数估计,后者提供发生比。
Logit 命令:Logit 因变量 变量1 变量2… 变量m/*二元非线性回归的基本命令,输出回归系数*/Logistic 命令:logistic 因变量 变量1 变量2… 变量m/*二元非线性回归的基本命令,输出发生比*/lfit/* lfit 是模型适定性诊断命令*/clogit 因变量 变量1 变量2… 变量m ,strata(配对编号变量) [or]/* clogit 是条件logistic 回归命令*/10.3 关于股利政策的logit 模型及解释use E:\stata\logit.dta/*打开stata 数据集*/(1)logit 命令. logit cashdum roa td size lagcashdum growth cg12 firstIteration 0: log likelihood = -753.6759Iteration 1: log likelihood = -464.64549Iteration 2: log likelihood = -413.47149Iteration 3: log likelihood = -384.32824Iteration 4: log likelihood = -376.73079Iteration 5: log likelihood = -376.20593Iteration 6: log likelihood = -376.20303Logistic regression Number of obs = 1116 LR chi2(7) = 754.95 Prob > chi2 = 0.0000 Log likelihood = -376.20303 Pseudo R2 = 0.5008------------------------------------------------------------------------------cashdum | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+----------------------------------------------------------------roa | 36.27163 3.999394 9.07 0.000 28.43296 44.11029 td | -.3322466 .4976051 -0.67 0.504 -1.307535 .6430414 size | .1079257 .0839493 1.29 0.199 -.0566119 .2724633 lagcashdum | 2.815261 .2006755 14.03 0.000 2.421944 3.208578growth | .4252429 .2686294 1.58 0.113 -.1012611 .9517469 cg12 | .1585007 .0477705 3.32 0.001 .0648722 .2521292 first | 1.665727 .5831852 2.86 0.004 .5227054 2.80875 _cons | -6.445765 1.332788 -4.84 0.000 -9.057982 -3.833548这里,log likelihood 即对数似然值,乘以2即为-2LL ,是模型的估计方法。
在进行逐步回归时,通过比较不同模型的-2LL ,判断模型的拟合程度。
取值越小,模型的适应性越好;取值越大,模型的效果越差。
Number of obs 是我们所使用的样本量。
LR chi2(7)即为卡方检验统计量,也就是回归模型无效假设(即所有协变量的发生比均为1)所对应的似然比检验量,其中的(7)为自由度,Prob > chi2是模型无效假设检验对应的P 值。
这两个指标与线性回归的F 统计量和其P 值的功能大体一致。
0.0000数值表明,该模型是显著的。
另一个统计量Pseudo R2是伪决定系数R 2。
虽不完全等于R 2,但大致提供模型中自变量对因变量变异的解释能力。
Coef.是每个自变量对应的系数估计。
在logistic 回归分析中,该系数为对数;Std.Err 即系数对应的标准误;OLS 通过t 检验来判断自变量对因变量的影响是否显著,logistic 模型使用z 检验来达到该目的。
因此,z 是单个系数检验的统计量;P>|z|是系数检验的P 值;最后两列为系数95%的置信区间。
二元logit 回归分析中系数的解释与多元线性回归分析中回归系数的解释并无不同,βi 表示,x i 改变一个单位时,logitP 的平均变化量。
Logit 回归中的常数项(β0)表示,在不接触任何潜在危险(或保护因素)条件下,因变量发生与不发生的概率之比的对数值。
Logit 回归中的回归系数(βi )表示,某一自变量改变一单位时,因变量发生与不发生时间的概率之比的对数变化值,即发生比(Odds Ratio )的对数值。
由于系数为对数,故不能像线性回归那样将其直接解释为自变量对因变量的影响程度。
只有将其转换为风险比后,系数才更有明确的意义。
比如,分析结果显示,size (单位为千元)的回归系数为0.11。
但我们不能将系数解释为size 每增加一单位,发放股利的概率增加11%。
事实上,我们并不知道规模对股利发放概率的影响程度,虽然我们知道其影响性质和显著水平。
就变量lagcashdum 来说,上期发放股利的公司的概率高于上期不发放股利的公司,但我们并不知道二者之间的差别有多大。
当自变量为连续性变量时(如size ),e (βi )表示xi 增加一个计量单位的对数比;当自变量为二分类变量时(如:lagcashdum ),发生/是=1,不发生/否=0,则logistic 回归中的系数即为是/否的对数值。
若上面的系数转化为风险比(Odds Ratio ),则可直接比较组间差异以及自变量对因变量的影响程度。
转化公式为:)1/()1/(0011p p p p OR --= (2)logistic 命令Stata 另外一个命令可以直接输出风险比:. logistic cashdum roa td size2 lagcashdum growth cg12 firstLogistic regression Number of obs = 1116LR chi2(7) = 754.95Prob > chi2 = 0.0000Log likelihood = -376.20303 Pseudo R2 = 0.5008------------------------------------------------------------------------------cashdum | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+----------------------------------------------------------------td | .7173104 .3569373 -0.67 0.504 .2704861 1.902258 size2 | 1.113965 .0935166 1.29 0.199 .9449608 1.313195 lagcashdum | 16.69753 3.350786 14.03 0.000 11.26774 24.74386 growth | 1.529962 .4109928 1.58 0.113 .903697 2.590231cg12 | 1.171753 .0559752 3.32 0.001 1.067023 1.286762first | 5.28952 3.08477 2.86 0.004 1.686584 16.58916roa | 5.66e+15 2.26e+16 9.07 0.000 2.23e+12 1.44e+19 ------------------------------------------------------------------------------Odds Ratio为自变量各自对应的风险比;Std.Err.即相应的风险比的标准差;z是单个风险比=1检验的z统计量;P>|z|是耽搁风险比=1检验的P值;最后两列为95%的置信区间。
