常见值概率曲线(利用累积频率的正态分布曲线)
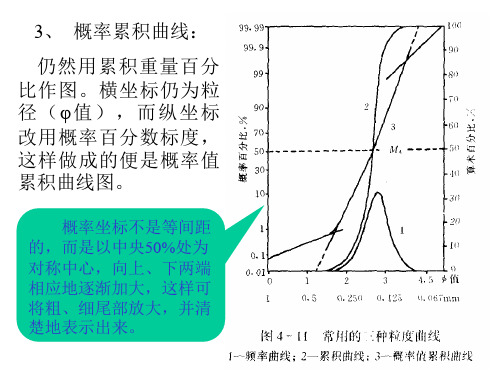
概率累积曲线
(2)标准偏差(σ1): 用标准偏差(σi)确定的六个分选级别: σ1<0.35,分选极好; σ1=0.35~0.50,分选好; σ1=0.50~0.71,分选较好;σ1=0.71~1.00,分选中等; σ1=1.00~2.00,分选较差;σ1=2.00~4.00,分选差; σ1>4.00,分选极差; 分选性的实际意义: 分选性的实际意义: 分选性的好坏也可以作为环境标志。沉积物的分 选程度与沉积环境的水动力条件有密切关系。总的来 说,从风成砂丘—海(湖)滩砂—河道砂—冰川和冲 积扇沉积,其分选程度依次变差。
2、标准偏差和分选系数: 标准偏差和分选系数是用来表示颗粒大小均匀程度 的参数。 (1)分选系数(SO): 式中P25 和P75 分别代表累积曲线上颗粒含量25%和 75%处所对应的颗粒直径。 当颗粒分选很好时,P25和P75两值很靠近,所以SO 值就接近于1;相反,SO值越大则说明分选性越差。 根据SO值可以划分分选等级:SO=1~2.5,分选好; SO=2.5~4.0,分选中等;SO>4.0,分选差。
峰值的等级界限: 峰值的等级界限: 值越大峰越尖,越小越平 KG<0.67,很平坦; KG =0.67~0.90,平坦; KG =0.90~1.11,中等(正态); KG =1.11~1.56,尖锐; KG =1.56~3.00,很尖锐; KG>3.00,非常尖锐。
二、粒度分析在区分沉积环境中的应用: (一)粒度判别函数及成因图解: 1、萨胡判别函数: 、萨胡判别函数:
3、偏度(SK1): 偏度是用来表示频率曲线对称性的参数, 实质上反映粒度分布的不对称程度的。
频率曲线按其对称形态特征可分为三类: 频率曲线按其对称形态特征可分为三类:
(1)正态: 峰两侧粗细粒径的百分比含量互相对应地减少, 形成以峰为对称轴的对称曲线。此时中值、平均粒径 和众数三者为同一数值,说明沉积物分选好。 SK1=0 (2)正偏态: 曲线形态不对称,峰偏向粗粒度一侧,细粒一侧 有一低的尾部,说明沉积物以粗组分为主,分选性变 差 。SK1>0 (3)负偏态: 曲线形态不对称,峰偏向细粒度一侧,粗粒一侧 有一低的尾部,说明沉积物以细组分为主,分选性变 差。SK1<0。
常态分布曲线和正态分布曲线[001]
![常态分布曲线和正态分布曲线[001]](https://img.taocdn.com/s3/m/9147610def06eff9aef8941ea76e58fafab045ea.png)
常态分布曲线和正态分布曲线常态分布曲线和正态分布曲线是统计学中经常使用的两种概率分布曲线。
这两种曲线在形状、特征以及应用领域上存在一些差异,但其核心思想是相同的。
本文将深入探讨常态分布曲线和正态分布曲线的异同点,并介绍它们在实际应用中的重要性。
首先,我们来了解一下常态分布曲线。
常态分布曲线又称为钟形曲线或高斯曲线,是一种在统计学中常见的概率分布曲线。
它的特点是在均值处有一个高峰,向两侧逐渐下降,呈现出对称的特点。
常态分布曲线的形状可以由其均值和标准差来确定。
均值决定了曲线的中心位置,而标准差则决定了曲线的宽度。
当标准差较大时,曲线相对较宽,而当标准差较小时,曲线相对较窄。
而正态分布曲线是常态分布曲线的特例,也被称为正态概率密度函数。
正态分布曲线是以均值为中心,自由度为1的对称分布曲线。
它呈钟形曲线状,左右两侧都延伸至无穷远,且曲线与x轴的交点在正负无穷远处。
正态分布曲线的面积在均值左右对称,且由标准差决定了曲线的陡峭程度。
正态分布曲线的面积在均值左右对称,且由标准差决定了曲线的陡峭程度。
常态分布曲线和正态分布曲线的应用广泛。
它们在统计学和概率论中被广泛用于描述连续型随机变量的分布。
常态分布曲线和正态分布曲线的形状可以通过概率分布参数来调整,从而适应不同的实际情况。
因此,它们在统计推断、抽样分析、质量控制和风险评估等领域中具有重要的应用价值。
在实际应用中,常态分布曲线和正态分布曲线还可以用于推断总体特征、研究变量之间的关系以及预测未来趋势。
例如,在市场营销中,可以利用常态分布曲线和正态分布曲线来分析顾客的消费行为,从而预测未来的销售额。
在制造业中,可以使用常态分布曲线和正态分布曲线来评估产品的质量控制,以确保产品符合标准要求。
在金融领域中,可以利用常态分布曲线和正态分布曲线来衡量投资风险和预测股票价格的涨跌。
总而言之,常态分布曲线和正态分布曲线是统计学中两种重要的概率分布曲线。
它们具有相似的形状和特征,但又有一些微妙的差异。
概率累积曲线

概率累积曲线
概率累积曲线是表示随机变量分布状态的数学曲线,描述了变量不同取值出现的频率。
概率累积曲线是一种折线图,它根据抽样数据绘制出来,表示给定一个随机变量X介于某
两个取值X1和X2之间的概率密度(或频率)随X的变化趋势及其概率累积的变化情况。
概率累积曲线可以用来表示变量的分布范围、离散程度等,也可以帮助理解变量的概
率变化情况,比直方图更加有效。
它的定义是:如果随机变量X的概率密度函数为f(x),则它的概率累积曲线C(x)定义为:
C(X) = P(X <x) = ∫_x^∞ f(x)dx
其中P(X<X)表示X取值不超过x的概率,是一个介于0-1之间的数值,可以用来衡量
X取值范围的离散程度。
概率累积曲线默认从x轴的负无穷处开始,即C(-∞)=0,再沿着X的变化逐渐累积至
P(X<X)=1,即C(∞)=1,概率累积曲线的特性就是从(-∞,0)到(∞,1)一直呈现出上升趋势。
概率累积曲线在许多统计学和数学研究中有着广泛的应用。
它可以用来计算两个变量
X和Y之间的相关性,测量样本数据分布统计特性,进行概率计算和相关性分析,测量样
本数据稳定性,以及其他大量用途。
《正态分布曲线》PPT课件

具有两头低、中间高、左右对称的基本特征
2.正态曲线的性质
ms ( x)
y
1 e
2s y
(
xm )2 2s 2
, x (, )
y
μ= -1
μ=1
σ=0.5
μ=0
σ=1
σ=2
-3 -2 -1 0 1 2 x -3 -2 -1 0 1 2 3 x -3 -2 -1 0 1 2 3 4 x
x=m
x=m
x=m
b
P(a X b) a m,s (x)dx
1.正态分布定义 y
如果对于任何实数 a<b,随机变量X满足:
b
0
ab
x
P(a X b) a m,s (x)dx
则称X 的分布为正态分布. 正态分布由参数m、s
唯一确定, m、s分别表示总体的平均数与标准差.
正态分布记作N( m,s2).其图象称为正态曲线.
S(-,-X)
S(X,)=S(-,-X)
X=m
正态曲线下的面概积率规律(重要)
• 对称区域面积相等。
S(-x1, -x2)
S(x1,x2)=S(-x2,-x1)
-x1 -x2 x2 x1
X=m
3.特殊区间的概率:
m s ( , ) 若X~N
,则对2 于任何实数a>0,概率
P(m a x ≤ m a)
总之,正态分布广泛存在于自然界、生 产及科学技术的许多领域中。
正态分布在概率和统计中占有重要地位。
2.正态曲线的性质
ms ( x)
1
e
(
xm )2 2s 2
2 s
y
ห้องสมุดไป่ตู้
y
正态性分析的方法总结

四、直方图
直方图,是一种二维统计图表,它的两个坐标分别是统 计样本和该样本对应的某个属性的度量。当直方图为钟 型分布时,则可判断其正态。
五、箱线图
箱形图又称为盒须图、盒式图或箱线图,是一种用作显 示一组数据分散情况资料的统计图。因型状如箱子而得 名。在各种领域也经常被使用,常见于品质管理。在箱 线图中,观察矩形位置和中位数,若矩形位于中间位置, 且中位数位于矩形的中间位置,则分布为正态或近似正 态,对称的;g2>3是分布的峰度比正态分布 的峰度低阔;g2<3时,表面分布的峰度比正态分布的峰 度高狭。当N>1000时,g2值才比较可靠
假设检验方法
一、Kolmogorov-Smirno(KS)检验(基于经验分布函数(ECDF)的检验)
Kolmogorov-Smirnov检验法是检验单一样本是否来自某一特定分布。比如检 验一组数据是否为正态分布。它的检验方法是以样本数Kolmogorov-Smirnov 检验法是检验单一样本是否来自某一特定分布。比如检验一组数据是否为正 态分布。它的检验方法是以样本数。 即对于假设检验问题: H0:样本所来自的总体分布服从某特定分布; H1:样本所来自的总体分布不服从某特定分布。
三、Q-Q图
Q-Q图是一种散点图,对应于正态分布的Q-Q图,就是由 标准正态分布的分位数为横坐标,样本值为纵坐标的散 点图。要利用QQ图鉴别样本数据是否近似于正态分布, 只需看QQ图上的点是否近似地在一条直线附近,而且该 直线的斜率为标准差,截距为均值。 用QQ图还可获得样 本偏度和峰度的粗略信息。
五、Anderson-Darling检验
是一种最小距离估计方式,也是估计偏离正态性的最有 效的统计量之一,对于样本量小于等于25很有效,大样 本可能被拒绝正态性,样本量大于等于200一般都会通过 Anderson-Darling检验.该检验对与偏态的尾部分布较敏 感。
05-概率分布-正态分布

而后根据指标的实际用途确定单侧或双侧界值,根
据研究目的和使用要求选定适当的百分界值,常用 95%。 .
双侧临界值:标准正态分布双侧尾部面积之和等于α 时所 对应的正侧变量值,记作Zα /2。
单侧临界值:标准正态分布单侧尾部面积等于α 时所对应 的正侧变量值,记作Zα 。
以不同的方法计算参考值范围:
3. 求上、下界值
下界: x 1.96s 117.4 1.9610.2 97.41( g / l ) 上界: x 1.96s 117.4 1.9610.2 137.39( g / l )
所以,该地健康女性血红蛋白的95%参考值范围是 (97.41,137.39)g/l。
体重频率密度
图5-1 体重频率密度图
图5-2 概率密度曲线示意图
故对连续性随机变量而言:
变量某区间取值的概率 = 正态曲线该变量区间的面 积
推 断:
测得一个孕妇体重在54-68kg的概率有多大? 孕妇体重在哪个范围内算是正常的呢?
一、正态分布的概念和 密度函数
正态分布( normal distribution):是描述连续型
X 1.64S X 1.96S
X 2.58S
X-1.28S
X 1.28S X 1.64S
X 2.33S
X-1.64S X-2.33S
举例1:调查某地120名健康女性血红蛋白,直方图显 示其分布近似正态,试估计该地健康女性血红蛋白 的95%参考值范围。 解析: 1. 分布近似正态 2. 过高过低均为异常 正态分布法求参考值范围 设定双侧界值
3. 标准正态分布区间(-2.58,2.58)的面积占总面积的99%
2.左半侧Z 值对应面积的查法:标准正态分布是以 0 为中 心左右对称,所以该表只计算曲线下一半的面积即可 。
正态分布曲线

卡方检验
总结词
卡方检验是一种非参数检验方法,用于检验正态分布曲线的假设。
详细描述
卡方检验通过比较实际观测频数与理论频数,计算卡方统计量,以检验数据是否符合正态分布。如果样本数据符 合正态分布,则卡方统计量将接近于期望值。卡方检验的优点是不需要假设数据符合特定的分布形式,因此适用 于更广泛的数据类型。
考试分数分布
分数集中
考试分数通常呈现正态 分布,即大部分考生成 绩集中在平均分附近, 高分和低分成绩占少数。
标准差
考试分数的标准差可以 反映成绩分布的离散程 度,标准差越小,成绩 越集中。
及格率
考试及格分数线通常设 定在正态分布的60分左 右,以确保大部分考生 能够通过。
股票价格波动
波动幅度
股票价格的波动幅度通常呈现正态分布,即大部分时间股票价格波动较小,极端波动的情 况较少。
特征
集中性
正态分布曲线下的面积大部分集中在均值附近,离均值越远概率 越小。
对称性
正态分布曲线关于y轴对称,即概率密度函数是偶函数。
均匀递增性
在均值左侧,曲线从负无穷增加到0;在均值右侧,曲线从0增加 到正无穷。
概率密度函数
01
正态分布的概率密度函数为高斯函数,也称为钟形曲线。
02
概率密度函数表示随机变量取某个值的概率密度,即单位区间
详细描述
Z检验基于正态分布的性质,通过计算样本数据的均值和标准 差,与理论值进行比较,以检验数据是否符合正态分布。如 果样本数据符合正态分布,则Z检验统计量将接近于标准正态 分布种常用的假设检验方法,用于检验正态分布曲线的假设。
详细描述
t检验基于样本数据的均值和标准差,通过计算t统计量,与临界值进行比较,以 检验数据是否符合正态分布。如果样本数据符合正态分布,则t检验统计量将接 近于标准正态分布的临界值。
《正态分布曲线》课件

使用Python绘制正态分布曲线
count, bins, ignored = plt.hist(data, 30, density=True)
plt.plot(bins, (1/(sigma * np.sqrt(2 * np.pi))) * np.exp(- (bins - mu)2 / (2 * sigma2)), linewidth=2, color='r')
密度等。正态分布曲线可以用来描述这些物理量的分布情况。
03
社会调查
在社会调查中,许多调查数据呈现正态分布特征,例如民意调查、市场
调查等。正态分布曲线可以用来描述这些调查数据的分布情况。
CHAPTER 05
正态分布曲线的扩展知识
正态分布的假设检验
假设检验基本原理
假设检验是统计学中用于判断样本数据是否符合某种假设的一种方法。在正态分布的情境 下,通常假设数据符合正态分布,然后通过检验统计量进行判断。
THANKS
[ 感谢观看 ]
置信区间的应用
置信区间在统计学中有着广泛的应用,如回归分析、方差分析、实验设计等。在正态分布的情境下,我 们可以通过计算置信区间来评估样本数据的可靠性和稳定性。
正态分布与其他分布的比较
01 02 03
正态分布的优势
正态分布是一种非常重要的概率分布,其概率密度函数具 有许多优良的性质,如对称性、可加性等。此外,许多自 然现象和随机变量都呈现出近似正态分布的特性,因此正 态分布在统计学中具有广泛的应用。
《正态分布曲线》ppt 课件
CONTENTS 目录
• 正态分布曲线的定义 • 正态分布曲线的性质 • 正态分布曲线的绘制 • 正态分布曲线的应用 • 正态分布曲线的扩展知识
