简谐振动的旋转矢量图.ppt
合集下载
《大学物理》第14章 振动

速度超前位移 /2 vmax = A = (k/m)1/2A
a = - 2A cos (t + ) = 2A cos (t + + )
加速度超前位移 amax = 2A = (k/m)A
上页 下页 返回 退出
相位和初相
相位 (t 0 ) :决定简谐运动状态的物理量。
其中v为物体 m 距平衡位置 x 处的速度。 忽略摩擦,总机械能 E 保持不变。随着 物体来回振动,势能和动能交替变化。
上页 下页 返回 退出
§ 14-3简谐振动的能量
在x = A 和 x = - A处,v = 0,
E = m(0)2/2 + kA2/2 = kA2/2 (14-10a) 简谐振子的总机械能正比于振幅的平方。
dx/dt = - A sin (t + ) d2x/dt2 = - 2 A cos (t + ) = - 2 x
0 = d2x/dt2 + (k/m) x = - 2 x + (k/m) x
(k/m - 2) x = 0 只有当 (k/m - 2) = 0 时,x不为零。因此
a = - (410 m/s2) cos(1650t). (c) 在t = 1.0010-3 s 时刻
x = A cos t
= (1.510-4 m) cos[(1650 rad/s)(1.0010-3 s)]
= (1.510-4 m) cos(1.650 rad/s) = -1.210-5 m.
上页 下页 返回 退出
§ 14-1 弹簧的振动
例题 14-1 汽车弹簧。当一个质量为200公斤的 一家四口步入一辆总质量为1200公斤的汽车 里,汽车的弹簧压缩了3厘米。(a) 假设汽车 里的弹簧可视为单个弹簧,弹簧劲度系数为 多少? (b) 如果承载了300公斤而不是200公 斤,则汽车将下降多少厘米?
a = - 2A cos (t + ) = 2A cos (t + + )
加速度超前位移 amax = 2A = (k/m)A
上页 下页 返回 退出
相位和初相
相位 (t 0 ) :决定简谐运动状态的物理量。
其中v为物体 m 距平衡位置 x 处的速度。 忽略摩擦,总机械能 E 保持不变。随着 物体来回振动,势能和动能交替变化。
上页 下页 返回 退出
§ 14-3简谐振动的能量
在x = A 和 x = - A处,v = 0,
E = m(0)2/2 + kA2/2 = kA2/2 (14-10a) 简谐振子的总机械能正比于振幅的平方。
dx/dt = - A sin (t + ) d2x/dt2 = - 2 A cos (t + ) = - 2 x
0 = d2x/dt2 + (k/m) x = - 2 x + (k/m) x
(k/m - 2) x = 0 只有当 (k/m - 2) = 0 时,x不为零。因此
a = - (410 m/s2) cos(1650t). (c) 在t = 1.0010-3 s 时刻
x = A cos t
= (1.510-4 m) cos[(1650 rad/s)(1.0010-3 s)]
= (1.510-4 m) cos(1.650 rad/s) = -1.210-5 m.
上页 下页 返回 退出
§ 14-1 弹簧的振动
例题 14-1 汽车弹簧。当一个质量为200公斤的 一家四口步入一辆总质量为1200公斤的汽车 里,汽车的弹簧压缩了3厘米。(a) 假设汽车 里的弹簧可视为单个弹簧,弹簧劲度系数为 多少? (b) 如果承载了300公斤而不是200公 斤,则汽车将下降多少厘米?
大学物理B(Ⅱ)旋转矢量

2
t 0.667s
x
A
00 7.5 A 2
A v
t0
例 一简谐运动的运动
曲线如图所示,求振动周
期.
t(s) t 0
A A2 0 A x
t 7.5
2π T T
t 7.5s
T 18s
例 已知谐振动的 A 、T ,求 1)如图简谐运动方
A'
44
因为 v0 0 ,由旋转矢量图可知 ' π 4
x Acos(t ) 0.0707cos(6.0t π)
4
例2 一质量为 0.01kg 的物体作简谐运动,其振
幅为 0.08m,周期为 4s ,起始时刻物体在 x 0.04m
处,向 Ox轴负方向运动(如图).试求
(1)t 1.0s 时,物体所处的位置和所受的力;
A/2 t ta
A 0 A x
t0
π ( π) 2π
3 33
tb
T
2π
T 3
的最短时间.
v
x/m
0.08 0.04 o 0.04 0.08
法一 设由起始位置运动到 x 0.04m 处所
需要的最短时间为 t
0.04 0.08cos(π t π) 23
t 0.667s
解法二
t 时刻
t
π3 π3
0.08 0.04 o 0.04
起始时刻
x/m
0.08
t π
3
π s1
x 0.08cos(π t π ) 23
m 0.01kg
v
x/m
0.08 0.04 o 0.04 0.08
x 0.08cos(π t π ) 23
t 1.0s 代入上式得 x 0.069m
t 0.667s
x
A
00 7.5 A 2
A v
t0
例 一简谐运动的运动
曲线如图所示,求振动周
期.
t(s) t 0
A A2 0 A x
t 7.5
2π T T
t 7.5s
T 18s
例 已知谐振动的 A 、T ,求 1)如图简谐运动方
A'
44
因为 v0 0 ,由旋转矢量图可知 ' π 4
x Acos(t ) 0.0707cos(6.0t π)
4
例2 一质量为 0.01kg 的物体作简谐运动,其振
幅为 0.08m,周期为 4s ,起始时刻物体在 x 0.04m
处,向 Ox轴负方向运动(如图).试求
(1)t 1.0s 时,物体所处的位置和所受的力;
A/2 t ta
A 0 A x
t0
π ( π) 2π
3 33
tb
T
2π
T 3
的最短时间.
v
x/m
0.08 0.04 o 0.04 0.08
法一 设由起始位置运动到 x 0.04m 处所
需要的最短时间为 t
0.04 0.08cos(π t π) 23
t 0.667s
解法二
t 时刻
t
π3 π3
0.08 0.04 o 0.04
起始时刻
x/m
0.08
t π
3
π s1
x 0.08cos(π t π ) 23
m 0.01kg
v
x/m
0.08 0.04 o 0.04 0.08
x 0.08cos(π t π ) 23
t 1.0s 代入上式得 x 0.069m
简谐振动演示09

2 1
2 A2
2 A1 A2 cos( 2 1 )
o
2 2 2
60
0
A
x
A A A 5 10 (m)
平衡位置 x = 0
55
关于谐振动的合成的计算
教材
下册书 P38 9-5 9-28 9-30
56
(二)、 同一直线上两个不同频率谐振动的合成
当 2 1时 2 1 2 1 x1
9-6
9-7
基训:P93 例1 习题:A卷:一 1. 2. B卷:一 1.
17
9-2、旋转矢量
1.设一矢量 OM 逆时针方向 匀速转动,角速为
OM A
y
y
M
A
t 0
2. t 时刻矢端 M 点的位
o
t 0 x
置(坐标) x A cos(t 0 ) y A sin( t 0 )
由此可见: 旋转矢量的端点在坐标轴上投影点的运 动为谐振动 旋转矢量旋转一周 投影点全振动一次
19
X
例1
一谐振动的相位为
3 3 3 画旋转矢量,指出其投影点 的位置
, 2
,
60
x
o
60
例2
质点在平衡位置向 x 轴正向运动,
画对应的旋矢,指出其相位是多 少? 3 ( )
t=0时与x轴
正方向夹角 t时刻与x轴
x
正方向夹角
t=0时 刻 与t时 夹角
相位 t +
平衡位置 x=0 t
简谐振动的解题方法:
1. 解析法 2. 图示法
x A cos(t )
3。旋转矢量法(几何法) x x
2 A2
2 A1 A2 cos( 2 1 )
o
2 2 2
60
0
A
x
A A A 5 10 (m)
平衡位置 x = 0
55
关于谐振动的合成的计算
教材
下册书 P38 9-5 9-28 9-30
56
(二)、 同一直线上两个不同频率谐振动的合成
当 2 1时 2 1 2 1 x1
9-6
9-7
基训:P93 例1 习题:A卷:一 1. 2. B卷:一 1.
17
9-2、旋转矢量
1.设一矢量 OM 逆时针方向 匀速转动,角速为
OM A
y
y
M
A
t 0
2. t 时刻矢端 M 点的位
o
t 0 x
置(坐标) x A cos(t 0 ) y A sin( t 0 )
由此可见: 旋转矢量的端点在坐标轴上投影点的运 动为谐振动 旋转矢量旋转一周 投影点全振动一次
19
X
例1
一谐振动的相位为
3 3 3 画旋转矢量,指出其投影点 的位置
, 2
,
60
x
o
60
例2
质点在平衡位置向 x 轴正向运动,
画对应的旋矢,指出其相位是多 少? 3 ( )
t=0时与x轴
正方向夹角 t时刻与x轴
x
正方向夹角
t=0时 刻 与t时 夹角
相位 t +
平衡位置 x=0 t
简谐振动的解题方法:
1. 解析法 2. 图示法
x A cos(t )
3。旋转矢量法(几何法) x x
简谐振动的动力学特征及运动学-PPT

• 动力学方程
d2 dt
x
2
2
x
0
9
§4-1 简谐振动的动力学特征
x Acos(t )
T 2π 取 0
x xt图
A
o
T
A
v vt 图
t
v A sin(t ) A
o
Tt
A cos(t π ) A
2
a a t图
a A 2 cos(t ) A 2
o
Tt
A 2 cos(t π ) A 2
两振动位相之差
=2- 1
•当=2k ,k=0,±1,±2…,两振动步调相同,称同相
•当=(2k+1) , k=0,±1,±2...
两振动步调相反,称反相
•0<<
2 超前于1 或 1滞后于2
位相差反映了两个振动不同程度的参差错落
•谐振动的位移、速度、加速度之间的位相关系
x
A cos( t
A sin(
§4-2 简谐振动的运动学
例题 质点沿x轴作谐振动, 周期T=s, t=0时, xo 2m ,o 2 2m / s,求振动方程。
解: x =Acos( t+ )
2 2
T
A
xo2
o2 2
2
cos 2
2
sin 2
2
3
4
得x 2cos( 2t 3 )m
4 32
dt 2
x Acos(t 0 )
cos(t
0
)
sin(t
0
2
)
令
'
0
2
x Asin(t ' )
简谐振动的运动规律也可用正弦函数表示.
旋转矢量

v
x/m
0.08 0.04 o 0.04 0.08
第九章 振 动
11
物理学
第五版
9-2 旋转矢量
已知 m 0.01kg, A 0.08 m,T 4 s
t 0, x 0.04 m, v0 0 求(1)t 1.0 s, x, F
解 A 0.08 m 2 π π s1
第九章 振 动
4
物理学
第五版
9-2 旋转矢量
用旋转矢量图画简谐运动的x t图
第九章 振 动
5
物理学
第五版
9-2 旋转矢量
讨论 相位差:表示两个相位之差
(1)对同一简谐运动,相位差可以给出 两运动状态间变化所需的时间.
x1 Acos(t1 )
x Acos(t )
2
2
(t ) (t )
(A) 0~π/2之间. (B) π/2~π之间. (C) π~3π/2之间. (D) 3π/2~2π之间。
解:位移向下为正。当小盘处在最低位置时刻有一个小
物体落到盘上,则振子系统向下还是向上运动?
考虑到新的平衡位置相对原平衡位置向下移动的距离小于 原振幅,位移接近正的最大值,速度向下。采用旋转矢量 法可知初相位在第四象限。
物理学
第五版
选择进入下一节:
本章目录
9-1 简谐运动 振幅 周期和频率 相位
9-2 旋转矢量
9-3 单摆和复摆
9-4 简谐运动的能量
9-5 简谐运动的合成
* 9-6 阻尼振动 受迫振动 共振
第九章 振 动
19
法一 设由起始位置运动到x= -0.04 m处所 需要的最短时间为t
v x/m
旋转矢量法求解简谐振动初相位

Ke y wo r d s: Ha r mo n i c Vi b r a t i o n Th e I n i t i a l P h a s e T h e Eo t a t i o n V e c t o r
简谐振动 是一种最基本 的振动形式 , ห้องสมุดไป่ตู้
但对 于一个 确定的简谐 振动来说 , 显 然 只 振 动 的 初位 置在 圆周上 的 对应位 置便 可 以求
Ab s t a c t : C o n t a i n s t h e t h r e e e l e me n t s o f t h e a mp J i t u d e, f r e q u e n c y ,p h a s e a n g l e k i n e ma t i c s e q u a t i o n o f s i mp l e h a r mo n i c v i b r a t i o n, a n d i n
丛 Q : !
工 业 技 术
Sc i e n c e a n d Te c h n o l o g y I n n o v a t i o n H e r a l d
旋 转 矢 量 法 求解 简谐 振 动初 相 位 ①
唐义思 ( 重庆人文科技学 院 重庆
摘
4 0 1 5 2 4 )
要: 简谐振 动的运动学方程中包含振 幅, 角频率, 初相位 三个要素, 而在这三个要 素中, 初相位的求解相对来说 b 较麻烦, 一般情况下都是
采用 公式法来求辟 初相 位, 但 这种方法 求解过程相当 麻烦并 容易 出 错, 在该文中 介绍 使用 旋转矢 量法来求解初相位 的方法, 使用 该方法 来求解
t h e s e t h r e e e l e me n t s , s o l v i n g t he i n i t i a l p h a s e o f r e l a t i v e l y t r o u b l e , u n d e r n o r ma l c i r c u ms t a n c e s a r e t h e f o r mu l a t o s o l v e t h e i ni t i a l p h a s e , b u t t h i s me t h o d i n s o l v i n g p r o c e s s c u mb e r s o me a n d p r o n e t o e r r o r ,i n t h i s p a p e r d e s c r i b e s t h e u s e o f r o t a t i o n v e c t o r me t h o d t o s e e k s o l ut i o n o f i n i t i a l p h a s e ,t he me t h o d i s u s e d t o s o l v e t h e i n i t i a l p ha s e i s v e r y s i mp l e ,t he o p e r a t i o n i s a l s o q u i t e s ma l 1 .
9-3 简谐运动的图示法

5 t =0 24 3
第九章 振 动
5 t =0 24 3
3)到达点P相应位置所需时间
t P= .6s 1
9
物理学
第五版
物理学
第五版
9-3 简谐运动的图示法
二 简谐运动的矢量图示法
旋转矢量:自
原点O作一矢量 A ( A A ),且 A
在Oxy平面内绕点O 作逆时针匀角速转
v
0.08 0.04
x/m
o
0.04
0.08
28
第九章 振 动
物理学
第五版
物理学
第五版
9-3 简谐运动的图示法
法二
t
时刻
t
π3 π3
起始时刻
x/m
0.08
2 3
0.08 0.04
o
0.04
π t 3
π3 1 t T T 2π 6
第九章 振 动
0.667 s
29
x/m
x A cos( t )
解一(解析法):
0.10 0.05
0
P 4.0 t/s
A 0.10m t 0 0 x0 0.05m
0.05 0.10 cos
=
v0 A sin 0
t1 4.0s x1 0m
,
3 π 0 0.10 cos(4 )
x/m
0.10 0.05
0
P t/s
4.0
第九章 振 动
21
物理学
第五版
物理学
第五版
9-3 简谐运动的图示法
x/m 0.10 0.05 0 P
x A cos( t )
第九章 振 动
5 t =0 24 3
3)到达点P相应位置所需时间
t P= .6s 1
9
物理学
第五版
物理学
第五版
9-3 简谐运动的图示法
二 简谐运动的矢量图示法
旋转矢量:自
原点O作一矢量 A ( A A ),且 A
在Oxy平面内绕点O 作逆时针匀角速转
v
0.08 0.04
x/m
o
0.04
0.08
28
第九章 振 动
物理学
第五版
物理学
第五版
9-3 简谐运动的图示法
法二
t
时刻
t
π3 π3
起始时刻
x/m
0.08
2 3
0.08 0.04
o
0.04
π t 3
π3 1 t T T 2π 6
第九章 振 动
0.667 s
29
x/m
x A cos( t )
解一(解析法):
0.10 0.05
0
P 4.0 t/s
A 0.10m t 0 0 x0 0.05m
0.05 0.10 cos
=
v0 A sin 0
t1 4.0s x1 0m
,
3 π 0 0.10 cos(4 )
x/m
0.10 0.05
0
P t/s
4.0
第九章 振 动
21
物理学
第五版
物理学
第五版
9-3 简谐运动的图示法
x/m 0.10 0.05 0 P
x A cos( t )
简谐振动
I
G A
H
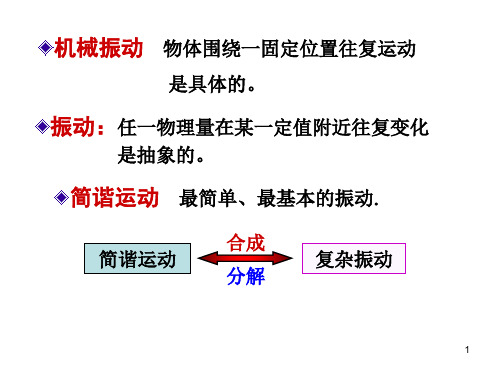
简谐振动曲线如图 以上描述简谐振动的方法称为简 谐振动的矢量图解法.
T
N
J
M
K T
L
t
12
旋转矢量
自Ox轴的原点 O作一矢量 A,使 它的模等于振动的 振幅A,并使矢量 A A 在 Oxy平面内绕点 t 0 O作逆时针方向的 o x0 x 匀角速转动,其角 x0 A cos 速度 与振动频率 相等,这个矢量就 叫做旋转矢量.
18
解:设物体沿x 轴作简谐振动
A = 10.0 cm = 0.100 m
m 0.500 当t = 0 时 ,x = A ,cos =1 ,
所以 x = 0.100 cos 8.00 t m
k
32.0
rad s
1
8.00 rad s
-1
即 =0
速度、加速度的最大值为 vm = A = 8.00×0.100 m s1 = 0.800 ms1 am= 2 A = (8.00)2 ×0.100 m s2 = 6.40 ms2 所以 v = 0.800 sin 8.00 t ms1
x0 A cos
2 A x0
2
2 v0
v0 Asin
v0 t an x0
10
对给定振动系统,周期由系统本身性质决定, 振幅和初相由初始条件决定.
讨论
已知 t
0, x 0, v 0 求
π A sin 0 取 2 o π x A cos( t ) A 2
π 2 v0 A sin 0
0 A cos
v
x
x
T 2
G A
H
简谐振动曲线如图 以上描述简谐振动的方法称为简 谐振动的矢量图解法.
T
N
J
M
K T
L
t
12
旋转矢量
自Ox轴的原点 O作一矢量 A,使 它的模等于振动的 振幅A,并使矢量 A A 在 Oxy平面内绕点 t 0 O作逆时针方向的 o x0 x 匀角速转动,其角 x0 A cos 速度 与振动频率 相等,这个矢量就 叫做旋转矢量.
18
解:设物体沿x 轴作简谐振动
A = 10.0 cm = 0.100 m
m 0.500 当t = 0 时 ,x = A ,cos =1 ,
所以 x = 0.100 cos 8.00 t m
k
32.0
rad s
1
8.00 rad s
-1
即 =0
速度、加速度的最大值为 vm = A = 8.00×0.100 m s1 = 0.800 ms1 am= 2 A = (8.00)2 ×0.100 m s2 = 6.40 ms2 所以 v = 0.800 sin 8.00 t ms1
x0 A cos
2 A x0
2
2 v0
v0 Asin
v0 t an x0
10
对给定振动系统,周期由系统本身性质决定, 振幅和初相由初始条件决定.
讨论
已知 t
0, x 0, v 0 求
π A sin 0 取 2 o π x A cos( t ) A 2
π 2 v0 A sin 0
0 A cos
v
x
x
T 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Aω
x Acos(t )
ωt A (t=0)
O
x x0 X
5
3. 旋转矢量法(参考圆法)
6
旋转矢量与振动曲线
7
例1:一个沿 x 轴作谐振动的弹簧振子, 振幅为 A,周期为T,若 t = 0 时,质点的 状态分别为:(1)x0=-A;(2)过平衡 位置向x正向运动;(3)过 x = A/2 处向x 负方向运动;试求相应的初相,并写出用
解:①
xx
A
0o
2
Tt
12
②正最大位移 x
A
o
0
A
o
t
③(1/2)位移处且速度为正值
x
A
A
O
2
t
=-
3
Axo
2
13
例3:一轻弹簧的倔强系数为k,其下悬有一 质量为m的盘子。现有一质量为M的物体从 离盘h高度处自由下落到盘子中并和盘子粘 在一起,于是盘子开始振动。(1)此时的 振动周期与空盘子做振动时的周期有何不同? (2)取平衡位置为原点,位移以向下为正, 并以弹簧开始振动时作为记时起点,写出余 弦函数形式的振动方程。
画出振动曲线。
x A
o -A
m
Ox x0 = 0
Tt
由这三个特征量可以写出振动方程:
x Acos(t )
2
T
4
3. 旋转矢量法
①矢量 A(模与振幅等值)以角速度ω
(与角频率等值)逆时针旋转。
② t = 0时, A 与x轴正向夹角为 .
用旋转矢量在x轴上的投影来表示谐振
动的位移x。
17
解: (1) T盘 2
m, k
T盘物 2
mM k
(2) y Acos( 2 t )
T
A
x02
v02
2
,
arctan(
v0
x0
)
15
有一质量为M的物体从离盘h高度处自由下落到盘 子中并和盘子粘在一起,于是盘子开始振动。取平
衡位置为原点,位移以向下为正,并以弹簧开始振 动时作为记时起点,写出余弦函数形式的振动方程。
=-
2
旋转矢量法:
=- 或 3
22
x
A
cos(
2
T
t
2
)
2
10
(3)解析法略 (过 x = A/2 处向x负方向运动)
旋转矢量法:
=
A
3
3
0 Ax
2
x
Acos(
2
T
t
3
)
11
例2:画出质点处于①平衡位置且速度小于 零,②正最大位移,③(1/2)位移处且速度 为正值的旋转矢量,说明初相的大小并画出 振动曲线。
1. 解析法
x Acos(t ) t =0
v Asin(t )
x0 Acos
v0 Asin
由此解出A,
Aarcxt02an(v022vx0 0 )
3
2. 曲线法
由振动曲线可知 振幅A,周期T
和初相 。
由振幅A,周期
T和初相 可以
)
A
cos(
2
T
t
)
(1)解析法(x0=-A)
由x0 Acos A, cos 1, =
旋转矢量法:
= 或-
x Acos( 2 t )
T
9
(2)解析法(过平衡位置向x正向运动)
x0
Acos
0
2
v0 Asin>0 sin<0
余弦函数表示的振动方程。
解:所求振动方程为
x
A cos( t
)
Aபைடு நூலகம்
cos(
2
T
t
)
8
例1:一个沿 x 轴作谐振动的弹簧振子,振幅为
A,周期为T,其振动方程用余弦函数表示。若
t = 0 时,质点的状态分别为:(1)x0=-A;试 求相应的初相,并写出振动方程。
解: x
A cos( t
14
例3:一轻弹簧的倔强系数为k,其下悬有一质量 为m的盘子。现有一质量为M的物体从离盘h高度
处自由下落到盘子中并和盘子粘在一起,于是盘 子开始振动。(1)此时的振动周期与空盘子做振 动时的周期有何不同?(2)取平衡位置为原点,
位移以向下为正,并以弹簧开始振动时作为记时 起点,写出余弦函数形式的振动方程。
第7章 机械振动
简谐振动的旋转矢量图
1
回顾: • 掌握简谐振动的判断方法。 • 掌握简谐振动的特征量。 • 掌握简谐振动的速度加速度。
x Acos(t )
2
7.1.3 A,ω, 的确定 x Acos(t )
ω由振动系统本身的性质所决定,
ω一定时 A, 由初始条件决定。
下落: v 2gh
碰撞:mv (m M )v0 t 0, y0 (2 1 )
A
y02
v02
2
,
1
2
O
h
y
arctan(
v0
y0
),
(2) y Acos( 2 t )
T
16
本节课小结: (1)A,ω, 的确定。 (2)掌握旋转矢量法。 作业:7-5
