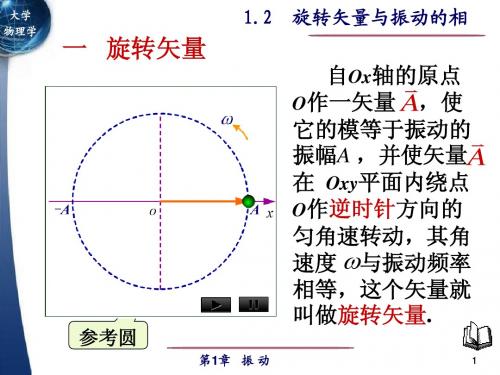
大学物理 旋转矢量
合集下载
大学物理-11第十一讲简谐振动、振动能量、旋转矢量法

振动方程 x0.15cos5tmxAcost
14
例:边长l的立方体木块浮于静水中,浸入水中部分 的高度为b。今用手将木块压下去,放手让其开始运 动。忽略水的阻力,证明木块作谐振动。 解:以水面为原点建立坐标OX。
任意时刻 F浮水(bx)l2g mgF浮ma
水 b l2g水 l2(bx)gm a
力使 减小.
mgsinmldd2t2
很小,sin mg
ml
d2
dt2
l m
f mg
d 2
dt 2
g
l
0
角谐振动
解为 0cos(t)
g T 2 l
l
g
12
例:如图所示装置,轻弹簧k =50N/m,滑轮 M =1kg,
半径 R =0.2m,物体 m =1.5kg。若将物体由平衡位置
X
P
xAcos(t)
◆可用该旋转矢量末端的投影点 P 的运动来表示简 谐振动。
16
旋转矢量法的应用
1.确定初位相 ●由初始位置 x0 确定旋转矢量两个可能的位置。 (特殊情况下只有一个位置) ●根据初始速度方向,由旋转矢量两个可能的位 置中确定初始位置,从而找出初相.。
A
Ox
17
例:确定下列情况的初位相 (a) 已知 t = 0 时,x = -A。 (b) 已知 t = 0时,x = 0,且向 x 轴正方向运动。 (c) 已知 t = 0,x = -A/2,且向 x 轴负方向运动。 (d) 已知 t = 0,x = -A/2,且向 x 轴正方向运动。
13
d2x dt2
k x0 m(1/2)m
d2x dt 2
14
例:边长l的立方体木块浮于静水中,浸入水中部分 的高度为b。今用手将木块压下去,放手让其开始运 动。忽略水的阻力,证明木块作谐振动。 解:以水面为原点建立坐标OX。
任意时刻 F浮水(bx)l2g mgF浮ma
水 b l2g水 l2(bx)gm a
力使 减小.
mgsinmldd2t2
很小,sin mg
ml
d2
dt2
l m
f mg
d 2
dt 2
g
l
0
角谐振动
解为 0cos(t)
g T 2 l
l
g
12
例:如图所示装置,轻弹簧k =50N/m,滑轮 M =1kg,
半径 R =0.2m,物体 m =1.5kg。若将物体由平衡位置
X
P
xAcos(t)
◆可用该旋转矢量末端的投影点 P 的运动来表示简 谐振动。
16
旋转矢量法的应用
1.确定初位相 ●由初始位置 x0 确定旋转矢量两个可能的位置。 (特殊情况下只有一个位置) ●根据初始速度方向,由旋转矢量两个可能的位 置中确定初始位置,从而找出初相.。
A
Ox
17
例:确定下列情况的初位相 (a) 已知 t = 0 时,x = -A。 (b) 已知 t = 0时,x = 0,且向 x 轴正方向运动。 (c) 已知 t = 0,x = -A/2,且向 x 轴负方向运动。 (d) 已知 t = 0,x = -A/2,且向 x 轴正方向运动。
13
d2x dt2
k x0 m(1/2)m
d2x dt 2
大学物理规范作业A(本一)振动解答

2
( D)
根据
1 2 E kA , 2
15 Ek E E P E 16
Ek 15 所以 : E 16
3
3.已知一简谐振动x1=4cos(10t+3π /5),另有一个 同方向简谐振动x2=6cos(10t+φ );若令两振动合成 的振幅最小,则φ 的取值应为:
( A)
3
,
7 ( B) , 5
7
三、计算题
1.作简谐振动的小球,速度最大值vm=3cm/s,振幅A=2cm , 若令速度具有正最大值的时刻为t=0,求(1)振动周期; (2)加速度最大值;(3)振动表达式。
x A cos(t ) 解:设振动方程为:
dx ⑴速度为 v A sin(t ) dt
x2 y2 1 2 。 2 A1 A2
由振动方程得 1 4 ,
2
4
所以 2 1 2 将其代入合振动轨迹方程:
x 2 y 2 2 xy 2 2 1 cos sin 2 1 2 2 A1 A2 A1 A2 x2 y2 质点的轨迹方程: 2 2 1 A1 A2
大学物理规范作业
总(07) 振 动
1
一、选择题 1.一质点作简谐振动,周期为T。当它由平衡位置 向x轴正向运动时,从二分之一最大位移到最大位 移处,这段路程所需要的时间为:
( A) T / 4 , ( B) T / 6, ( C) T / 8 , ( D) T / 12
(B)
分析: 当质点从二分之一最大位移处运动到最大 位移处时,旋转矢量转过的角度为:
vm 0.03 1.5rad / s A 0.02
( D)
根据
1 2 E kA , 2
15 Ek E E P E 16
Ek 15 所以 : E 16
3
3.已知一简谐振动x1=4cos(10t+3π /5),另有一个 同方向简谐振动x2=6cos(10t+φ );若令两振动合成 的振幅最小,则φ 的取值应为:
( A)
3
,
7 ( B) , 5
7
三、计算题
1.作简谐振动的小球,速度最大值vm=3cm/s,振幅A=2cm , 若令速度具有正最大值的时刻为t=0,求(1)振动周期; (2)加速度最大值;(3)振动表达式。
x A cos(t ) 解:设振动方程为:
dx ⑴速度为 v A sin(t ) dt
x2 y2 1 2 。 2 A1 A2
由振动方程得 1 4 ,
2
4
所以 2 1 2 将其代入合振动轨迹方程:
x 2 y 2 2 xy 2 2 1 cos sin 2 1 2 2 A1 A2 A1 A2 x2 y2 质点的轨迹方程: 2 2 1 A1 A2
大学物理规范作业
总(07) 振 动
1
一、选择题 1.一质点作简谐振动,周期为T。当它由平衡位置 向x轴正向运动时,从二分之一最大位移到最大位 移处,这段路程所需要的时间为:
( A) T / 4 , ( B) T / 6, ( C) T / 8 , ( D) T / 12
(B)
分析: 当质点从二分之一最大位移处运动到最大 位移处时,旋转矢量转过的角度为:
vm 0.03 1.5rad / s A 0.02
大学物理B(Ⅱ)旋转矢量

2
t 0.667s
x
A
00 7.5 A 2
A v
t0
例 一简谐运动的运动
曲线如图所示,求振动周
期.
t(s) t 0
A A2 0 A x
t 7.5
2π T T
t 7.5s
T 18s
例 已知谐振动的 A 、T ,求 1)如图简谐运动方
A'
44
因为 v0 0 ,由旋转矢量图可知 ' π 4
x Acos(t ) 0.0707cos(6.0t π)
4
例2 一质量为 0.01kg 的物体作简谐运动,其振
幅为 0.08m,周期为 4s ,起始时刻物体在 x 0.04m
处,向 Ox轴负方向运动(如图).试求
(1)t 1.0s 时,物体所处的位置和所受的力;
A/2 t ta
A 0 A x
t0
π ( π) 2π
3 33
tb
T
2π
T 3
的最短时间.
v
x/m
0.08 0.04 o 0.04 0.08
法一 设由起始位置运动到 x 0.04m 处所
需要的最短时间为 t
0.04 0.08cos(π t π) 23
t 0.667s
解法二
t 时刻
t
π3 π3
0.08 0.04 o 0.04
起始时刻
x/m
0.08
t π
3
π s1
x 0.08cos(π t π ) 23
m 0.01kg
v
x/m
0.08 0.04 o 0.04 0.08
x 0.08cos(π t π ) 23
t 1.0s 代入上式得 x 0.069m
t 0.667s
x
A
00 7.5 A 2
A v
t0
例 一简谐运动的运动
曲线如图所示,求振动周
期.
t(s) t 0
A A2 0 A x
t 7.5
2π T T
t 7.5s
T 18s
例 已知谐振动的 A 、T ,求 1)如图简谐运动方
A'
44
因为 v0 0 ,由旋转矢量图可知 ' π 4
x Acos(t ) 0.0707cos(6.0t π)
4
例2 一质量为 0.01kg 的物体作简谐运动,其振
幅为 0.08m,周期为 4s ,起始时刻物体在 x 0.04m
处,向 Ox轴负方向运动(如图).试求
(1)t 1.0s 时,物体所处的位置和所受的力;
A/2 t ta
A 0 A x
t0
π ( π) 2π
3 33
tb
T
2π
T 3
的最短时间.
v
x/m
0.08 0.04 o 0.04 0.08
法一 设由起始位置运动到 x 0.04m 处所
需要的最短时间为 t
0.04 0.08cos(π t π) 23
t 0.667s
解法二
t 时刻
t
π3 π3
0.08 0.04 o 0.04
起始时刻
x/m
0.08
t π
3
π s1
x 0.08cos(π t π ) 23
m 0.01kg
v
x/m
0.08 0.04 o 0.04 0.08
x 0.08cos(π t π ) 23
t 1.0s 代入上式得 x 0.069m
1-1 简谐运动方程及旋转矢量

热力学基础 f ( P,V , T ) C
气体动理论 k N 0
量子物理
E = h
xPx h
1 2 1 mv f(v)dv kT 2 2 h E , p h
第九章
振动
Chapter 9 Vibration
String theory: Theory of everything
2. 简谐运动的运动学分析 运动方程 x A cos(t )
(1)描述简谐运动的基本物理量 A——振幅
ω——角频率
T——周期 ν——频率 ωt +φ——相位
A A
x
T
o
t
初相:表示物体在初 始时刻的振动状态。
v A sin( t )
a A cos(t )
l
FT m
g l
o
Acos(t )
问题:
P
Simple Harmonic Motion (SHM)
5. 简谐运动的两个实例——单摆和复摆 (2)复摆 5
o
d 2 转动正向 2 sin 0 dt
2
lc
*
C
P
( C点为质心)
mglc J
3. 旋转矢量法
简谐运动 平衡位置 振幅 角频率 初相 相位 位移 旋转矢量 圆心
A
t
o
x
半径 角速度
初始角度 t时刻的夹角
半径在x轴上的投影
例1 已知某简谐运动的振动曲线如图所示, 位移的单位为cm,时间单位为s,则此简谐振 动的
振幅 A= 角频率
2 cm
4 rad s 1 3
大学物理规范作业(本一)15解答

A2 = A A1
利用旋转矢量法,如图示, 可得第二个谐振动得振幅为10cm, 与第一个谐振动的位相差为
10
A2
A1
3
A 合 20
π 10 3
6
π
2
3.质量为m 劲度系数为k的弹簧振子在t=0时位于最大 3.质量为m,劲度系数为k的弹簧振子在t=0时位于最大 质量为 t=0 k 位移x=A x=A处 该弹簧振子的振动方程为x=_________ t ) x=_________; 位移x=A处,该弹簧振子的振动方程为x=_________; A cos( m π m 时振子第一次达到x=A/2处;t = ____________时振子第一次达到x=A/2处 在t1=____________时振子第一次达到x=A/2 2 π π m 3 k ____________时振子的振动动能和弹性势能正好相等 时振子的振动动能和弹性势能正好相等; (____________时振子的振动动能和弹性势能正好相等; n + ) 2 4 k 3π m ______________时振子第一次以振动的最大速度 t3=______________时振子第一次以振动的最大速度 k k 2 沿轴正方向运动. vm=___________沿轴正方向运动. ___________沿轴正方向运动 A m k 解:依题意 ω = ,0 = 0 m k 弹簧振子的振动方程: = A cos(ωt + 0 ) = A cos( x t) 振子第一次到达x=A/2处时位相变化=π/3,有:
π
则O点振动方程为 y 0 = A cos(ω t + ) 2 入射波波动方程为:
2
π
x π 2πx π y1 = A cos[ω (t ) + ] = A cos(ωt + ) u 2 λ 2
1.2旋转矢量与振动的相
1A : A 0.12 m 2 1 2 : S T 3 :
当t=0时,x0=0.06m, 带入表达式
x x0 0.12cos 0.06
1 cos 2
,
3
17
第1章 振 动
大学 物理学
1.2
旋转矢量与振动的相
另一个初始条件:当t=0时,质点向x轴正向运动
v0 0 x A coswt v A sinwt
即: 当t=0时,
v0 A sin 0
3
sin 0 3
x 0.12 cos t m 或x 0.12 cos t SI 3 18 3 振动 第1章
A2
O
x1
x
x A1
反相
T
A2 o - A2 -A1
t
x2
此种情况称为两振动反相(振动步调完全相反)
第1章 振 动
12
大学 物理学
1.2
旋转矢量与振动的相
Q2 t 0
3若 2 1 0
X2先于x1到达平衡位置、 负的最大等 称为: X2超前于x1, x1 落后于 X2
x
x
o
a
若此时 矢量末端在m点:则当t ,x , v 0
第1章 振 动
8
大学 物理学
1.2
旋转矢量与振动的相 m
x
A A2
a
b
v0
t
tb
a
o
A
v
A
p1 x o Ap2t A
2 n
v0
可以证明:当矢量处于x轴上面,则v<0;反之则v>0 由x~t图象可知:当处于b点时,v<0 所以此时矢量末端在m点
大学物理旋转矢量

极坐标表示法
极坐标与平面角
旋转矢量在极坐标系中由一个起点、一个长度和一个平面角唯一确定。平面角表示矢量旋转的方向和角度。
旋转矢量的运算
在极坐标系中,可以通过加减、数乘等运算得到新的旋转矢量。
直角坐标表示法
直角坐标与平面矢量
旋转矢量在直角坐标系中由三个分量唯一确定,这三个分量表示矢量在x、y、z轴上的投影。
结论总结
总结实验结果,得出结论,并指出实验的局限性和未来改进的方向 。
THANKS
感谢观看
旋转矢量的积分
当一个旋转矢量在某区间内进行积分时,其 结果为该区间内所有点处的切线方向与该区 间内所有点处的速度方向一致的点所组成的
线段。
04
旋转矢量在物理中的应用
角动量守恒定律
角动量定义
物体的转动惯量和转动半径的乘积称为角动量。
角动量守恒定律
在没有外力矩作用的情况下,物体的角动量保持不变。
旋转矢量表示
旋转矢量的应用领域
物理学
旋转矢量在物理学中广泛应用于描述物体的 旋转运动,如刚体的转动、电磁场的旋涡等 。
工程学
在机械工程、航空航天等领域,旋转矢量可以用于 分析物体的动态平衡、稳定性等问题。
电子技术
在电子技术中,旋转矢量可以用于描述信号 的相位、频率等参数,以及进行数字信号处 理。
02
旋转矢量的表示方法
03
旋转矢量的运算规则
加法运算规则
平行四边形法则
当两个旋转矢量相加时,以两个矢量的末端 为起点,分别画出平行四边形的两个相邻边 ,连接对角线,得到的结果是两个旋转矢量 相加后的矢量。
三角形法则
当两个旋转矢量相加时,以一个矢量的起点 为起点,画另一个矢量的平行线,得到的结 果是两个旋转矢量相加后的矢量。
大学物理-旋转矢量
3.初始条件
t 0 x0 A v0 0
A A cos cos 1
x o A
y
x
A
A
o
xo
A
物理学教程 (第二版)
l
t
第五章 机械振动
5 – 2 旋转矢量
4.初始条件
x
t 0
o
x0 0
v0 0
0 A cos cos 0
/ 2 , 3 / 2
y
x
3 A
o
2
x
以 o为 原点 旋转矢 量A的端点
x 在 轴上的
投影点的运 动为简谐运 动.
第五章 机械振动
5 – 2 旋转矢量
物理学教程 (第二版)
x Acos(t )
旋 转 矢量 A的
x 端点在
轴上的投 影点的运 动为简谐 运动.
第五章 机械振动
5 – 2 旋转矢量
y vm t π
2
t
0
an
a v
m 0.01kg o 0.04 0.08
x 0.08cos(π t π ) 23
t 1.0s 代入上式得 x 0.069m
F kx m 2x 1.70103 N
第五章 机械振动
5 – 2 旋转矢量
物理学教程 (第二版)
(2)由起始位置运动到 x 0.04m 处所需要
A
x
物理学教程 (第二版)
vm A an A 2
x Acos(t )
v A cos(t π )
2
a A2 cos(t )
第五章 机械振动
5 – 2 旋转矢量
用旋转矢量表示简谐运动初相
1.初始条件 t 0 x0 A v0 0
t 0 x0 A v0 0
A A cos cos 1
x o A
y
x
A
A
o
xo
A
物理学教程 (第二版)
l
t
第五章 机械振动
5 – 2 旋转矢量
4.初始条件
x
t 0
o
x0 0
v0 0
0 A cos cos 0
/ 2 , 3 / 2
y
x
3 A
o
2
x
以 o为 原点 旋转矢 量A的端点
x 在 轴上的
投影点的运 动为简谐运 动.
第五章 机械振动
5 – 2 旋转矢量
物理学教程 (第二版)
x Acos(t )
旋 转 矢量 A的
x 端点在
轴上的投 影点的运 动为简谐 运动.
第五章 机械振动
5 – 2 旋转矢量
y vm t π
2
t
0
an
a v
m 0.01kg o 0.04 0.08
x 0.08cos(π t π ) 23
t 1.0s 代入上式得 x 0.069m
F kx m 2x 1.70103 N
第五章 机械振动
5 – 2 旋转矢量
物理学教程 (第二版)
(2)由起始位置运动到 x 0.04m 处所需要
A
x
物理学教程 (第二版)
vm A an A 2
x Acos(t )
v A cos(t π )
2
a A2 cos(t )
第五章 机械振动
5 – 2 旋转矢量
用旋转矢量表示简谐运动初相
1.初始条件 t 0 x0 A v0 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
l
o
A A cos
cos 1
A
y
x
A
o
x o
A
t
第五章 机械振动
4.初始条件 t0 x0 0 v0 0
5 – 2
旋转矢量
x
o
物理学教程 (第二版)
l
0 A cos cos 0
y
x
A
/ 2 , 3 / 2
oA
3 2
5 – 2
旋转矢量
物理学教程 (第二版)
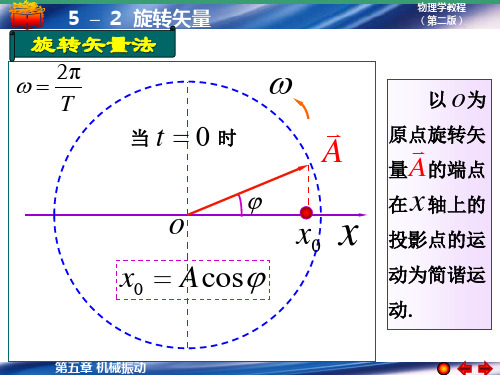
旋转矢量法
2π T
当
t 0
时
A
以 o为 原点旋转矢
量 A的端点
在
o
x0 A cos
第五章 机械振动
x0
x
x 轴上的
投影点的运 动为简谐运 动.
5 – 2
旋转矢量
物理学教程 (第二版)
2π T
A
t t
时
以 o为 原点旋转矢
x1 A1 cos(t 1 )
x2 A2 cos(t 2 )
2 1
为其它
(t 2 ) (t 1 )
0 同步
π 反相
超前
落后
x
x
x
o
t
第五章 机械振动
o
t
o
t
5 – 2
旋转矢量
物理学教程 (第二版)
例1 如图所示,一轻弹簧的右端连着一物体,弹 1 簧的劲度系数 k 0.72N m ,物体的质量 m 20g .
(1)把物体从平衡位置向右拉到 x 0.05 m 处停 下后再释放,求简谐运动方程; A (2)求物体从初位置运动到第一次经过 处时的 2 速度; (3)如果物体在 x 0.05 m 处时速度不等于零, 而是具有向右的初速度 v0 0.30m s1 ,求其运动方程.
2π π 1 s T 2
第五章 机械振动
5 – 2
旋转矢量
物理学教程 (第二版)
A 0.08 m
t 0, x 0.04m
π v0 0 3
0.08 0.04
2π π 1 s T 2
代入 x
0.04 0.08cos
A cos(t ) π 3
A
π 3
x/m
0.08 π ) 3
0.04 π x 0.08 cos( t 2
o
第五章 机械振动
5 – 2
旋转矢量
物理学教程 (第二版)
m 0.01kg
0.08 0.04
v
o
0.04 0.08
x/m
π π x 0.08 cos( t ) 2 3
t 1.0s 代入上式得
x A cos(t )
6.0s 1
A x
2 0
v
2 0 2
o
0.0707m
π 4
x
A'
由旋转矢量图可知 π 4
π x A cos(t ) 0.0707 cos( 6.0t ) 4
第五章 机械振动
5 – 2
旋转矢量
物理学教程 (第二版)
t
量 A的端点
o
x
x0
x
在
x 轴上的
投影点的运 动为简谐运 动.
x A cos(t )
第五章 机械振动
5 – 2
旋转矢量
物理学教程 (第二版)
x A cos(t )
矢量 A的
端点在 轴上的投 影点的运 动为简谐 运动.
第五章 机械振动
旋转
x5 – 2Fra bibliotekAo
v A sin t
A 2
x
0.26m s
第五章 机械振动
1
(负号表示速度沿 Ox 轴负方向)
5 – 2
旋转矢量
物理学教程 (第二版)
(3)如果物体在 x 0.05 m 处时速度不等于零, 而是具有向右的初速度 v0 0.30m s1 ,求其运动方程. 解
旋转矢量
x
o
物理学教程 (第二版)
l
A
y
2
A
x
/ 2 , 3 / 2
o
x o
t
v0 A sin 0, sin 0 取 / 2
第五章 机械振动
3.初始条件
t0 x0 A v0 0
5 – 2
旋转矢量
x
A
物理学教程 (第二版)
x o
t
v0 A sin 0, sin 0 取 3 / 2
第五章 机械振动
5 – 2
旋转矢量
物理学教程 (第二版)
讨论
相位差:表示两个相位之差 .
1)对同一简谐运动,相位差可以给出两运动状 态间变化所需的时间. (t 2 ) (t1 )
旋转矢量
物理学教程 (第二版)
用旋转矢量表示简谐运动初相 1.初始条件 x t0 o A x0 A v0 0
l
A A cos
cos 1
第五章 机械振动
A
o
y
x
A
0
x
o
t
2.初始条件 t0 x0 0 v0 0 0 A cos cos 0
5 – 2
2
x 0.069 m
F kx m x 1.70 103 N
第五章 机械振动
5 – 2
旋转矢量
物理学教程 (第二版)
(2)由起始位置运动到 x 0.04 m 处所需要 的最短时间.
v
0.08 0.04
x/m
0.04 0.08
o
法一 设由起始位置运动到 x 0.04 m 处所 需要的最短时间为 t
第五章 机械振动
o
A
x
5 – 2
旋转矢量
物理学教程 (第二版)
A (2)求物体从初位置运动到第一次经过 处时的 2 速度;
解
x A cos(t ) A cos(t )
A
x 1 cos( t ) A 2 π 5π t 或 3 3 π 由旋转矢量图可知 t 3
π π 0.04 0.08 cos( t ) 2 3
t 0.667 s
第五章 机械振动
5 – 2 解法二
旋转矢量
物理学教程 (第二版)
t
时刻
π 3
t
o
起始时刻
π 3
0.04 0.08
x/m
0.08 0.04
π t 3
第五章 机械振动
π 1 s 2
t 0.667 s
x/m
o
第五章 机械振动
0.05
5 – 2 解 (1)
旋转矢量
物理学教程 (第二版)
x A cos(t )
1
k 0.72N m m 0.02kg
6.0s
1
A 0.05 m
由旋转矢量图可知
0
x A cos(t )
0.05 cos 6.0t m
旋转矢量
物理学教程 (第二版)
y vm
t
0
an
π t 2
A
vm A
v a
an A
2
x
x A cos(t )
π v A cos( t ) 2
a A cos(t )
2
第五章 机械振动
5 – 2
例2 一质量为 0.01kg 的物体作简谐运动,其振 幅为 0.08 m ,周期为 4s ,起始时刻物体在 x 0.04 m 处,向 Ox 轴负方向运动(如图).试求 (1) t
1.0s
时,物体所处的位置和所受的力;
v
0.08 0.04
x/m
0.04 0.08
o
解
A 0.08 m
x A cos(t1 ) x A cos(t2 )
t t 2 t1
x
A
A2
a
b
π 3
Ab
o
A
v
t
A
0 A
x
π 3 1 t T T 2π 6
2
Aa A
第五章 机械振动
5 – 2
旋转矢量
物理学教程 (第二版)
2)对于两个同频率的简谐运动,相位差表示它 们间步调上的差异.(解决振动合成问题)
