简谐振动旋转矢量表示法.ppt
合集下载
大学物理B(Ⅱ)旋转矢量

2
t 0.667s
x
A
00 7.5 A 2
A v
t0
例 一简谐运动的运动
曲线如图所示,求振动周
期.
t(s) t 0
A A2 0 A x
t 7.5
2π T T
t 7.5s
T 18s
例 已知谐振动的 A 、T ,求 1)如图简谐运动方
A'
44
因为 v0 0 ,由旋转矢量图可知 ' π 4
x Acos(t ) 0.0707cos(6.0t π)
4
例2 一质量为 0.01kg 的物体作简谐运动,其振
幅为 0.08m,周期为 4s ,起始时刻物体在 x 0.04m
处,向 Ox轴负方向运动(如图).试求
(1)t 1.0s 时,物体所处的位置和所受的力;
A/2 t ta
A 0 A x
t0
π ( π) 2π
3 33
tb
T
2π
T 3
的最短时间.
v
x/m
0.08 0.04 o 0.04 0.08
法一 设由起始位置运动到 x 0.04m 处所
需要的最短时间为 t
0.04 0.08cos(π t π) 23
t 0.667s
解法二
t 时刻
t
π3 π3
0.08 0.04 o 0.04
起始时刻
x/m
0.08
t π
3
π s1
x 0.08cos(π t π ) 23
m 0.01kg
v
x/m
0.08 0.04 o 0.04 0.08
x 0.08cos(π t π ) 23
t 1.0s 代入上式得 x 0.069m
t 0.667s
x
A
00 7.5 A 2
A v
t0
例 一简谐运动的运动
曲线如图所示,求振动周
期.
t(s) t 0
A A2 0 A x
t 7.5
2π T T
t 7.5s
T 18s
例 已知谐振动的 A 、T ,求 1)如图简谐运动方
A'
44
因为 v0 0 ,由旋转矢量图可知 ' π 4
x Acos(t ) 0.0707cos(6.0t π)
4
例2 一质量为 0.01kg 的物体作简谐运动,其振
幅为 0.08m,周期为 4s ,起始时刻物体在 x 0.04m
处,向 Ox轴负方向运动(如图).试求
(1)t 1.0s 时,物体所处的位置和所受的力;
A/2 t ta
A 0 A x
t0
π ( π) 2π
3 33
tb
T
2π
T 3
的最短时间.
v
x/m
0.08 0.04 o 0.04 0.08
法一 设由起始位置运动到 x 0.04m 处所
需要的最短时间为 t
0.04 0.08cos(π t π) 23
t 0.667s
解法二
t 时刻
t
π3 π3
0.08 0.04 o 0.04
起始时刻
x/m
0.08
t π
3
π s1
x 0.08cos(π t π ) 23
m 0.01kg
v
x/m
0.08 0.04 o 0.04 0.08
x 0.08cos(π t π ) 23
t 1.0s 代入上式得 x 0.069m
简谐振动的动力学特征及运动学-PPT

• 动力学方程
d2 dt
x
2
2
x
0
9
§4-1 简谐振动的动力学特征
x Acos(t )
T 2π 取 0
x xt图
A
o
T
A
v vt 图
t
v A sin(t ) A
o
Tt
A cos(t π ) A
2
a a t图
a A 2 cos(t ) A 2
o
Tt
A 2 cos(t π ) A 2
两振动位相之差
=2- 1
•当=2k ,k=0,±1,±2…,两振动步调相同,称同相
•当=(2k+1) , k=0,±1,±2...
两振动步调相反,称反相
•0<<
2 超前于1 或 1滞后于2
位相差反映了两个振动不同程度的参差错落
•谐振动的位移、速度、加速度之间的位相关系
x
A cos( t
A sin(
§4-2 简谐振动的运动学
例题 质点沿x轴作谐振动, 周期T=s, t=0时, xo 2m ,o 2 2m / s,求振动方程。
解: x =Acos( t+ )
2 2
T
A
xo2
o2 2
2
cos 2
2
sin 2
2
3
4
得x 2cos( 2t 3 )m
4 32
dt 2
x Acos(t 0 )
cos(t
0
)
sin(t
0
2
)
令
'
0
2
x Asin(t ' )
简谐振动的运动规律也可用正弦函数表示.
简谐运动的旋转矢量描述法

π
4
A g a'*
h' * g'* *
t f O b*' T T f'* 3T T 5T
e
c' 4* 2*e' 4
4
-A
d*'
T 2 (旋转矢量旋转一周所需的时间)
用旋转矢量图画简谐运动的 x t 图
T 2π (旋转矢量旋转一周所需的时间)
二、旋转矢量法对相位的表示
若某时刻t,测得质点的位移为x =A/2,向OX轴负方
简谐运动的旋转 矢量表示法
一、简谐运动的旋转矢量表示法
P
t=t
t+
o
A t=0
A
x·
x
x Aco(s t )
x Aco(s t )
旋 转 矢量 A的
x 端点在
轴上的投
影点的运
动为简谐
运动.
x Acos(t )
用旋转矢量图画简谐运动的 x t 图
x
Ah
a
bO
c -Ad
x
x Acos(t )
向运动
M
A
O 3P
X
M
三、旋转矢量法对相位差的表示
A2
A1
O
相位差 2 1 2kπ
x
(k 0,1, 2,)
两个振动同相,步调相同
A1
O
A2
相位差 2 1 (2k 1)π
x
(k 0,1,)
两个振动反相,步调相反
例题 两个同方向、同频率的谐振动,频率为2s-1,
当第一个振子从平衡位置向正向运振动的相位差。
解:
2 1
A 2
t
o
02简谐振动的运动学精品PPT课件

19
t t
o
A
t
x
x Acos(t )
点旋以转o矢为量原A
的端点在 x 轴
上的投影点的
运动为简谐运
动.
第4章 机械振动
4–2 简谐振动的运动学
20
y
vm t π
2
t an
A
0
a
v
x
x Acos(t )
vm A v A sin(t )
an A 2
a A 2 cos(t )
雌性蚊子 雄性蚊子 苍蝇 黄蜂
355~415 455~600 330 220
第4章 机械振动
4–2 简谐振动的运动学
例 如图所示系统(细线的质 量和伸长可忽略不计),细线 静止地处于铅直位置,重物位 于O 点时为平衡位置.
若把重物从平衡位置O 略 微移开后放手, 重物就在平衡 位置附近往复的运动.这一振 动系统叫做单摆. 求单摆小角 度振动时的周期.
12
x 简谐运动中, x和 v
间不存在一一对应的关系. A
x A cos(t 0 ) o
v A sin(t 0 ) A
v v
T 2
xt 图
v T t
3、位相和初位相 t 0
1) t 0 (x, v) 存在一一对应的关系;
2)相位在 0 ~ 2π 内变化,质点无相同的运动状态;
相差 2nπ (n为整数 )质点运动状态全同.(周期性)
4–2 简谐振动的运动学
1
一 简谐振动的运动学方程
d2x 2x 0
dt 2
x Acos(t 0 )
cos(t
0
)
sin(t
0
2
)
旋转矢量和振动合成
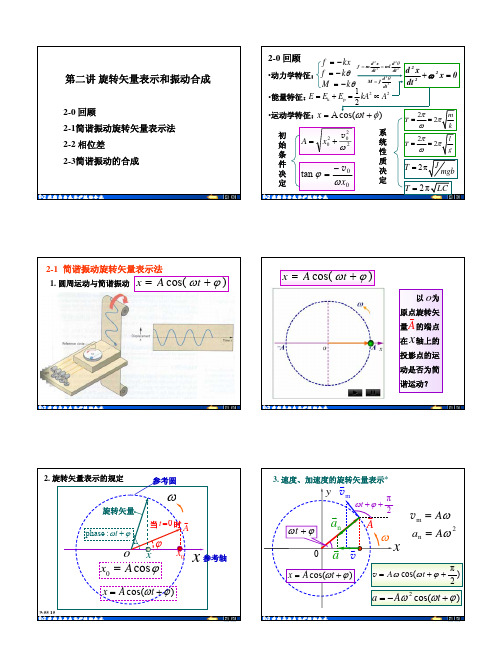
x = A 2 ,且向x 负向运动。
如:位相ωt2 +φ = 3π 2,问状态? x =0 ,且向 x 正向运动。
ω
Aπ
3
o
x
例2. 已知状态求位相(特别是初位相)
如:t =0,x0 = A 2,v0>0,求φ ?
φ = 5π 3 或 φ = −π 3
A2
如:t = 0 ,x0 = − A 2 ,v0 <0,求 φ ? −A 2 o
x/m
x/m
v A2 Δϕ
v A1
0.2
21
0.1
o
1234
56
t/s
解: A = 0.2m
ϕ1
=
−
π 2
T = 4s ω = 2π = π (1/s)
T2
x1
=
π 0.2 cos(
2
t
−
π 2
)
(SI)
Δt
=
Δϕ ω
φ2
=
−
π 3
x2
=
பைடு நூலகம்
π 0.2 cos(
2
t
−
π )
3
(SI)
(
=
π π
6 2
=
1 3
ω
Av
v A3
vϕ3
x ϕ
v
ϕ
A2
2
ϕ1 A1
多个同方向同频率简谐运动合成仍为简谐运动
11:00 10 9-2 旋转矢量表示和振动合成
x1 = A0 cos ω t
x2 = A0 cos( ω t + Δϕ )
xxNL3 ==LAA00ccooss[(ωωt
t +
如:位相ωt2 +φ = 3π 2,问状态? x =0 ,且向 x 正向运动。
ω
Aπ
3
o
x
例2. 已知状态求位相(特别是初位相)
如:t =0,x0 = A 2,v0>0,求φ ?
φ = 5π 3 或 φ = −π 3
A2
如:t = 0 ,x0 = − A 2 ,v0 <0,求 φ ? −A 2 o
x/m
x/m
v A2 Δϕ
v A1
0.2
21
0.1
o
1234
56
t/s
解: A = 0.2m
ϕ1
=
−
π 2
T = 4s ω = 2π = π (1/s)
T2
x1
=
π 0.2 cos(
2
t
−
π 2
)
(SI)
Δt
=
Δϕ ω
φ2
=
−
π 3
x2
=
பைடு நூலகம்
π 0.2 cos(
2
t
−
π )
3
(SI)
(
=
π π
6 2
=
1 3
ω
Av
v A3
vϕ3
x ϕ
v
ϕ
A2
2
ϕ1 A1
多个同方向同频率简谐运动合成仍为简谐运动
11:00 10 9-2 旋转矢量表示和振动合成
x1 = A0 cos ω t
x2 = A0 cos( ω t + Δϕ )
xxNL3 ==LAA00ccooss[(ωωt
t +
10-1 简谐振动的矢量图示法
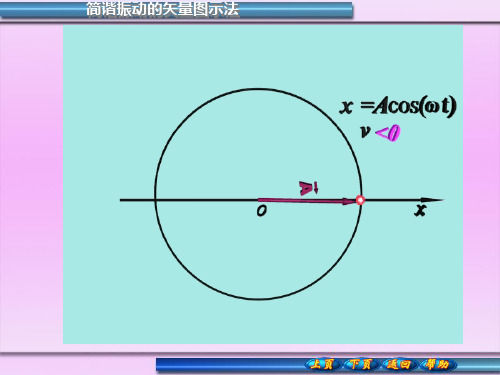
简谐振动的矢量图示法
简谐振动的矢量图示法
A 的长度
振幅A
A旋转的角速度
振动圆频率 O
ω
M
A
t 0
P
X
x
A 旋转的方向
逆时针方向
A 与参考方向x 的夹角 振动相位
M 点在 x 轴上投影(P点)的运动规律:
x Acos(t 0 )
矢量OM 的端点 M 所画的圆叫参考圆。 矢量 OM 0 是 t = 0 时刻的位置,它与 x 轴的夹角φ叫初相位。 简谐振动的参考圆和矢量表示方法十分形
x
A 2
A 1.0
0
t
补例 1一谐振动的振动曲线如图所示。
求:ω 、φ 以及振动方程。
x
A 2
A 1.0
0
t
补例 1一谐振动的振动曲线如图所示。
求:ω 、φ 以及振动方程。
x
A 2
A 1.0
0
t
t
=
0时
{
x 0
=
A 2
补例 1一谐振动的振动曲线如图所示
求:ω 、φ 以及振动方程。
x
A 2
A 1.0
解:已知 A = 0.12 m,T = 2s,
ω = 2π/T = π ( rad/s ).
( t =1 s ) B ’
ω
(1) 初态 t = 0 时,
x = 0.06, v >0, 初相 φ = -π/3 ,
-0.06
●
O 0.06
●
φ
Δφ
x (m
运动表达式为:
( t = 5/3 s) B
A(t=0)
速度v 0
P
A
x
M
简谐振动的矢量图示法
A 的长度
振幅A
A旋转的角速度
振动圆频率 O
ω
M
A
t 0
P
X
x
A 旋转的方向
逆时针方向
A 与参考方向x 的夹角 振动相位
M 点在 x 轴上投影(P点)的运动规律:
x Acos(t 0 )
矢量OM 的端点 M 所画的圆叫参考圆。 矢量 OM 0 是 t = 0 时刻的位置,它与 x 轴的夹角φ叫初相位。 简谐振动的参考圆和矢量表示方法十分形
x
A 2
A 1.0
0
t
补例 1一谐振动的振动曲线如图所示。
求:ω 、φ 以及振动方程。
x
A 2
A 1.0
0
t
补例 1一谐振动的振动曲线如图所示。
求:ω 、φ 以及振动方程。
x
A 2
A 1.0
0
t
t
=
0时
{
x 0
=
A 2
补例 1一谐振动的振动曲线如图所示
求:ω 、φ 以及振动方程。
x
A 2
A 1.0
解:已知 A = 0.12 m,T = 2s,
ω = 2π/T = π ( rad/s ).
( t =1 s ) B ’
ω
(1) 初态 t = 0 时,
x = 0.06, v >0, 初相 φ = -π/3 ,
-0.06
●
O 0.06
●
φ
Δφ
x (m
运动表达式为:
( t = 5/3 s) B
A(t=0)
速度v 0
P
A
x
M
振动力学教程PPT课件

动的叠加-----------谐波分析
•
2、非周期:利用傅立叶积分作谐波分析
• δ函数又称为单位脉冲函数-----它的性质、应用
示成一系列简谐振
第22页/共35页
第一节:简谐振动及其表示方法
•一、简谐振动的表示方法
• (一)正弦函数表示
2、A、ω、Φ ------简谐振动三要素
第23页/共35页
第24页/共35页
船舶的模态分析和强度分析,飞行器的结构振动和声疲劳分析等。
3) 在土木建筑、地质工程中:建筑、桥梁等结构物的模态分析,地震
引起结构物的动态响应,爆破技术的研究等。
4) 在医学、生物工程中:脑电波、心电波、脉搏波动等的信号处理等。
第12页/共35页
2途径:
1)从具体的工程对象提炼出力学模型 2)建立数学模型------应用力学知识建立所研究问题的数学模型 3)对数学模型进行分析和计算,求出请确、近似或数值解。 4) 比较------将计算结果与工程问题的实际现象或实验研究的测试结果进行 比较,考察理论结果是否解决该工程问题,如不能解决而数学模型及求解均无错 误,则需要修改力学模型重复上述过程。
第9页/共35页
5 随机振动
20世纪50年代,航空和航天工程的发展对振动力学提出了更高 的要求,确定性的力学模型无法处理包含随机因素的工程问题----如大气湍流引起的飞机颤振、喷气噪音导致飞行器表面结构 的声疲劳、火箭运载工具有效负荷的可靠性等。工程的需要迫使 人们用概率统计的方法研究承受非确定性载荷的机械系统和结构 的响应、稳定性和可靠性等, 从而 形成了随机振动这一振动力 学的重要组成部分。 在工程问题中振动信号的采集和处理是随机振动理论应用的前提, 由于计算机的迅速发展和快速第1傅0页/立共35叶页 变换算法的出现,随机振动
第四章振动下
结论: 结论:
振子在振动过程中, (1) 振子在振动过程中,动能和势能分别随时间 变化,但任一时刻总机械能保持不变。 变化,但任一时刻总机械能保持不变。 (2) 动能和势能的变化频率是弹簧振子振动频 率的两倍。 频率一定时, (3)频率一定时,谐振动的总能量与振幅的平方 成正比。(适合于任何谐振系统) 。(适合于任何谐振系统 成正比。(适合于任何谐振系统) 弹性势能
小结:
描述简谐振动的三种方法: 描述简谐振动的三种方法: 运动方程,振动曲线,旋转矢量。 运动方程,振动曲线,旋转矢量。
的简谐振动, 例1:一物体沿 轴作振 幅为 A 的简谐振动,若初始时该球的 :一物体沿x轴作振 状态为( ) ;(2)在平衡位置且向X轴正方向运动 轴正方向运动; 状态为(1)X0= -A;( )在平衡位置且向 轴正方向运动; ;( 处向X轴负方向运动;(4) 轴负方向运动;( (3)在 X0=1/2 A 处向 轴负方向运动;( )在 ) / 方向运动。试用旋转矢量法确定相应的初相位。 处向正 方向运动。试用旋转矢量法确定相应的初相位。 3π r ϕ = ϕ =π
k = m
得
X
g b
mg
b, v 0 = 0
g t+π) b
A =b, φ = π
[ 例2] 一谐振动的振动曲线如图所示。 一谐振动的振动曲线如图所示。
ω 以及振动方程。 求: ϕ 0 以及振动方程。
−
π
x
x
A 2
3r
A
1.0
0
解:
t
r A
A
π
2
x
π
3
t=
A x0 = = A cos ϕ 0 2 0时 v 0 = − ω A sin ϕ 0 > 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x 0.104m v 0.188m / s
a 1.03m / s2
A
t 时刻
x/m
0.12 0.06 o π0.06 0.12
3
A
起始时刻
第十一章 振 动
15
大学物 理学
11-1 简谐振动的旋转矢量表示法
(3)从初始时刻开始第一次通过平衡位 置的时刻.
通过平衡位置时,x=0,则由位移公式:
12
大学物 理学
11-1 简谐振动的旋转矢量表示法
又 v Asin(t ) 则 v0 Asin()
根据题意 v0 0
则
3
简谐运动表达式为:
x 0.12 cos( t )
3
0.12 0.06 o π0.06 0.12
v0
0,
3
3
A
x/m
第十一章 振 动
13
大学物 理学
11-1 简谐振动的旋转矢量表示法
相位的意义: 表征任意时刻(t)物体振动状态
(相貌). 物体经一周期的振动,相位改变 2π .
第十一章 振 动
7
大学物 理学
11-1 简谐振动的旋转矢量表示法
讨论 ➢ 相位差:表示两个相位之差
(1)对同一简谐运动,相位差可以给出 两运动状态间变化所需的时间.
x1 Acos(t1 ) x2 Acos(t2 )
0 0.12 cos(t )
3
所以:t (2k 1) , k 1, 2,
3
2
k
t
6
第十一章 振 动
16
大学物 理学
11-1 简谐振动的旋转矢量表示法
第一次过平衡点时,k=1,所以:
5
t 6 5 0.83(s)
6
A
x/m
0.12 0.06 o π0.06 0.12
3
A
起始时刻
(t2 ) (t1 )
t
t2
t1
第十一章 振 动
8
大学物 理学
x
Aa
A2
b
o A v
11-1 简谐振动的旋转矢量表示法
t A
tb
x o A ta A
2
π
3
t π 3T 1 T 2π 6
第十一章 振 动
9
大学物 理学
11-1 简谐振动的旋转矢量表示法
(2)对于两个同频率的简谐运动,相位 差表示它们间步调上的差异(解决振动合成
A
t
x
x Acos(t )
点旋以转o矢为量原A
的端点在 x轴
上的投影点的
运动为简谐运
动.
第十一章 振 动
4
大学物 理学
11-1 简谐振动的旋转矢量表示法
y
vm t π
2
t an
A
O a v x
vm A
v A sin(t )
an A 2
x Acos(t )
a A2 cos(t )
大学物 理学
11-1 简谐振动的旋转矢量表示法
旋转矢量
自Ox轴的原点 O作一矢量 A,使 它 振的 幅模A ,等并于使振矢动量的A
在 Oxy平面内绕点
O作逆时针方向的
匀角速转动,其角
速度 与振动频率
相等,这个矢量就 叫做旋转矢量.
第十一章 振 动
1
大学物 理学
11-1 简谐振动的旋转矢量表示法
x Acos(t )
(2)t T / 4 时,质点的位置、速度、加速度
此简谐运动的速度为:
v Asin(t ) 0.12 sin( t )
3
加速度为:
a 2 A cos(t ) 0.12 2 cos( t )
3
第十一章 振 动
14
大学物 理学
11-1 简谐振动的旋转矢量表示法
将t=T/4=0.5s分别代入位移、速度、加 速度的公式,得:
点旋以转矢o为量原A
的端点在 x轴
上的投影点的
运动为简谐运
动.
第十一章 振 动
2
大学物 理学
11-1 简谐振动的旋转矢量表示法
t 0
o
A
x0 x
x0 Acos
点旋以转o矢为量原A
的端点在 x轴
上的投影点的
运动为简谐运
动.
第十一章 振 动
3
大学物 理学
11-1 简谐振动的旋转矢量表示法
t t
o
第十一章 振 动
5
大学物 理学
11-1 简谐振动的旋转矢量表示法
用旋转矢量图画简谐运动的x t图
第十一章 振 动
6
大学物 理学
11-1 简谐振动的旋转矢量表示法
相位 t
x A cos(t )
v A sin(t )
相位 (位相) (t) t
初相位 t 0时,(t)
问题).
x1
A1
cos(t
1
)
x A cos(t )
2
2
2
(t 2 ) (t 1)
2
1
第十一章 振 动
10
大学物 理学
2 1
0同步 x
11-1 简谐振动的旋转矢量表示法
超前
π 反相 为其它 落后
x
x
o
to
o
t
t
第十一章 振 动
11
大学物 理学
11-1 简谐振动的旋转矢量表示法
例 一质点沿x轴作简谐运动,振幅 A=0.12 m,周期T=2 s,当t=0时,质点对平衡 位置的位移x0=0.06m.此时刻质点向x正向运动。 试求:
(1)此简谐运动的表达式
解 A 0.12 m 2 π s1
T
t 0,x0 0.06 m
代入 x Acos(t )
π
3
第十一章 振 动
第十一章 振 动
17
