专题:力的正交分解法和力的分解的几种常见的情况
力的分解与正交分解

F2
F
sin
θ
F1
NEXT
第五节
力的分解
2、具体实例
例3:按力的作用效果分解并根据图示求分力的大小。
60
o
30
o
F2 F1
sin 30
o
G1 G G2 G
G1 G sin 30
o
G 2
F1
G1
30
o
G2
cos 30
o
G 2 G cos 30
o
3 2
F
Fx F cos
x
物体处于平衡态满足方程为:
F y合 0
Fx合 0
NEXT
第五节
力的分解
4、正交分解法
(2)例1:如图,重为500N的人通过滑轮的轻绳牵引重200N的物 体,当绳与水平成60o角时,物体静止,不计滑轮与绳子的摩擦, 求地面对人的支持力和摩擦力。
y
FT 1 FT cos 100 N FT 2 FT sin 100 3 N FT
NEXT
第五节
力的分解
2、具体实例
例题1.把一个物体放在倾角为θ 的斜面上,物体并没有在 重力作用下竖直下落,从力的作用效果看,应怎样将重力分解 ?两个分力的大小与倾角有什么关系?
G1
sin
G1 G G2 G
G1 G sin G 2 G cos
G
G2
cos
NEXT
第五节
力的分解
2、具体实例
例1:按力的作用效果分解并根据图示求分力的大小。
sin cos
专题:力的正交分解法和力的分解的几种常见的情况
专题:力的正交分解法和力的分解的几种常见的情况 一.力的正交分解法1.定义:将一个力分解为两个相互垂直的分力的方法称为正交分解法。
2.目的:将力的合成化简为同向、反向或垂直方向的分力,便于运用代数运算公式解决矢量的运算,“分解”的目的是为了更好地“合成”。
3.适用情况:适用于计算三个或三个以上的力的合成。
4.步骤:(1)建立坐标系:以共点力的作用点为坐标原点,直角坐标系x 轴和y 轴的选择应使尽量多的力在坐标轴上。
(2)正交分解各力:将每一个不在坐标轴上的力分解到x 轴和y 轴上,并求出各分力的大小。
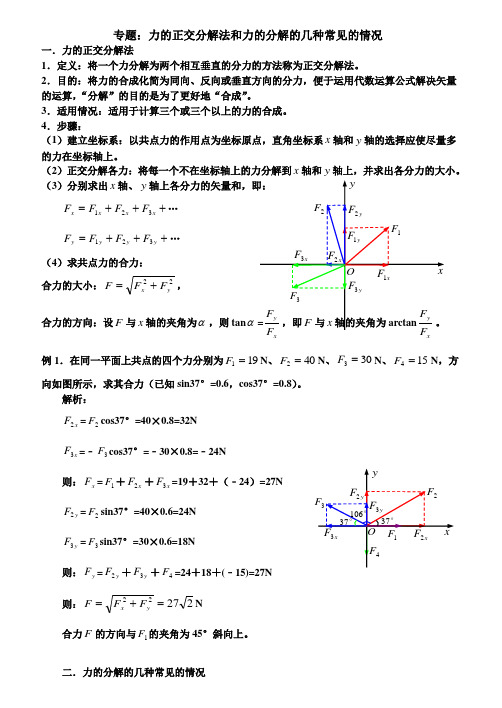
(3)分别求出x 轴、y+++=x x x x F F F F 321… +++=y y y y F F F F 321… (4)求共点力的合力: 合力的大小:22y x F F F +=,合力的方向:设F 与x 轴的夹角为α,则tan αxx例1.在同一平面上共点的四个力分别为191=F N 、402=F N 、303=F N 、154=F N ,方向如图所示,求其合力(已知sin37°=0.6,cos37°=0.8)。
解析:x F 2=2F cos37°=40×0.8=32N x F 3=﹣3F cos37°=﹣30×0.8=﹣24N则:x F =1F +x F 2+x F 3=19+32+(﹣24)=27Ny F 2=2F sin37°=40×0.6=24N y F 3=3F sin37°=30×0.6=18N则:y F =y F 2+y F 3+4F =24+18+(﹣15)=27N 则:22722=+=y x F F F N合力F 的方向与1F 的夹角为45°斜向上。
二.力的分解的几种常见的情况1.已知两个分力的方向(在同一直线上的情况除外),有唯一解。
2.已知一个分力的大小和方向,有唯一解。
(完整)1力的正交分解法及其应用

又f =μN;
③
联立①②③得F=μGB+FA(cos θ-μsin θ). 可见,随着θ不断减小,水平力F将不断增大.
答案 随着θ不断减小,水平力F将不断增大
返回
练习8如图1所示,重物的质量为m,轻细绳AO和BO的 A端、B端是固定的,平衡时AO水平,BO与水平面的夹
角为θ,AO的拉力F1和BO的拉力F2的大小是多少?
为θ3,绳子的张力为F3。不计摩擦。则( A.θ1=θ2 =θ3 B.θ1= θ2<θ3 C.F1>F2>F3 D.F1=F2<F3
)
θθ
θ
答案:BD
拓展练习1如图所示,质量为m的物体在与竖直方向成 θ角的恒力F作用下沿粗糙墙面向上匀速运动,求物 体与墙壁间的动摩擦因数。
F θ
F G cos - sin
正交分解力的目的: 化复杂的矢量运算为普通的代数运算。便于运
用普通代数运算公式来解决矢量的运算。
基本思想: 正交分解法求合力,运用了“欲合先分”的策
略,即先分解再合成,降低了运算的难度,是一种 重要物理思维方法。
五、典例 求合力
例1一个物体受到四个力的作用,已知F1=1N,方向
正东;F2=2N,方向东偏北600,F3= 3 3 N,方向西
解题步骤 1、画出物体的受力图 2、建立直角坐标系 3、正交分解各力
4、别写出x、y方向的方程
5、根据方程求解
练习2质量为m的物体在与水平方向成θ角的恒力F作 用下,沿水平天花板向右做匀速直线运动。物体与天 花板间动摩擦因数为μ。请写出物体受摩擦力大小的 表达式。
F mg sin cos
练习3如图所示,用绳AO和BO吊起一个重100N的物体, 两绳AO、BO与竖直方向的夹角分别为30o和40o,求绳 AO和BO对物体的拉力的大小。
力的合成与分解知识点总结

力的合成与分解知识点总结力是物理学中的一个重要概念,力的合成与分解是解决力学问题的基础。
下面我们来详细总结一下力的合成与分解的相关知识点。
一、力的合成1、合力的概念如果一个力作用在物体上产生的效果跟几个力共同作用在物体上产生的效果相同,这个力就叫做那几个力的合力,那几个力就叫做这个力的分力。
2、共点力如果几个力都作用在物体的同一点,或者它们的作用线相交于一点,这几个力就叫做共点力。
3、力的合成法则(1)平行四边形定则两个力合成时,以表示这两个力的线段为邻边作平行四边形,这两个邻边之间的对角线就代表合力的大小和方向。
(2)三角形定则将两个分力首尾相接,连接始端与末端的有向线段就表示合力的大小和方向。
4、合力的计算(1)已知两个分力的大小和方向,求合力的大小和方向,直接运用平行四边形定则或三角形定则计算。
(2)已知两个分力的大小和夹角θ,合力的大小可以通过公式:$F =\sqrt{F_1^2 + F_2^2 + 2F_1F_2\cos\theta}$计算,合力的方向可以通过三角函数关系求得。
5、合力的范围(1)两个力的合力范围:$|F_1 F_2| \leq F \leq F_1 + F_2$。
(2)三个力的合力范围:先求出其中两个力的合力范围。
再看第三个力在这个范围内的情况,从而确定三个力的合力范围。
二、力的分解1、力的分解的概念求一个已知力的分力,叫做力的分解。
2、力的分解遵循的原则力的分解是力的合成的逆运算,同样遵循平行四边形定则或三角形定则。
3、力的分解的方法(1)按照力的实际作用效果进行分解。
例如,放在斜面上的物体受到的重力可以分解为沿斜面方向向下的分力和垂直斜面方向向下的分力。
(2)正交分解法将一个力沿着互相垂直的两个方向进行分解。
4、力的分解的唯一性(1)已知两个分力的方向,有唯一解。
(2)已知一个分力的大小和方向,有唯一解。
(3)已知两个分力的大小,其解的情况可能有:两力之和大于合力时,有两解。
_力的分解知识点与习题及答案

力的分解基本知识点与练习题基本知识点一、分力的概念1、几个力,如果它们共同产生的效果跟作用在物体上的一个力产生的效果相同,则这几个力就叫做那个力的分力(那个力就叫做这几个力的合力)。
2、分力与合力是等效替代关系,其相同之处是作用效果相同;不同之处是不能同时出现, 在受力分析或有关力的计算中不能重复考虑。
二、力的分解1、力的分解的概念:求一个已知力的分力叫做力的分解。
2、力的分解是力的合成的逆运算。
同样遵守力的平行四边形定则:如果把已知力F作为平行四边形的对角线,那么,与力F共点的平行四边形的两个邻边就表示力F的两个分力F1和F2。
3、力的分解的特点是:同一个力,若没有其他限制,可以分解为无数对大小、方向不同的力(因为对于同一条对角线.可以作出无数个不同的平行四边形),通常根据力的作用效果分解力才有实际意义。
4、按力的效果分解力F的一般方法步骤:(1)根据物体(或结点)所处的状态分析力的作用效果(2)根据力的作用效果,确定两个实际分力的方向;(3)根据两个分力的方向画出平行四边形;(4)根据平行四边形定则,利用学过的几何知识求两个分力的大小。
也可根据数学知识用计算法。
三、对一个已知力进行分解的几种常见的情况和力的分解的定解问题将一个力F分解为两个分力,根据力的平行四边形法则,是以这个力F为平行四边形的一条对角线作一个平行四边形。
在无附加条件限制时可作无数个不同的平行四边形。
这说明两个力的合力可唯一确定,一个力的两个分力不是唯一的。
要确定一个力的两个分力,一定有定解条件。
假设合力F一定1、当俩个分力F1已知,求另一个分力F2,如图F2有唯一解。
2、当俩个分力F1, F2的方向已知,求这俩个力,如图F1,F2有唯一解3、当俩个分力F1,F2的大小已知,求解这俩个力。
A、当F1F2一组解。
B、F1F2,无解。
C、F1F2,俩个解。
4、当一个分力的方向已知,另一个大小未知。
①2sinθ,无解。
②2sinθ,一个解。
力的合成和分解

力的合成和分解力是物体之间相互作用的结果,在物理学中扮演着重要的角色。
而力的合成和分解是研究力的基本性质及其应用的关键概念。
本文将详细讨论力的合成和分解的概念、原理和实际应用。
一、力的合成力的合成是指将两个或多个力的作用效果视为一个总的力的作用效果。
这是因为多个力的合成效果等于这些力的矢量和。
在数学上,力的合成可以看作是矢量的加法。
具体而言,如果有两个力F₁和F₂作用于同一物体上,它们可以通过以下方法合成:1. 图解法:在纸上将力的矢量F₁和F₂按照一定比例画出来,然后将它们首尾相连,形成一个三角形。
通过测量这个三角形的边长,可以得到力的合力的大小和方向。
2. 分解成分向量法:将力F₁沿某个坐标轴分解为两个分量F₁₁和F₁₂,将力F₂沿同一坐标轴分解为两个分量F₂₁和F₂₂。
然后,将这些分量相互相加,得到合力的大小和方向。
二、力的分解力的分解是指将一个力分解为两个或多个互相垂直的力的过程。
通过力的分解,我们可以研究物体在不同方向上受到的力的情况。
在实际应用中,力的分解常常用于解析力的问题以及计算物体的平衡条件。
常见的力的分解方法有:1. 正交分解法:将力按某个坐标系的轴方向进行分解,得到与该轴方向垂直的两个分力。
这样,原来的力可以表示为这两个分力的矢量和。
2. 三角函数分解法:利用三角函数的性质,将力分解为两个互相垂直的力。
通常选择水平和垂直方向为坐标轴,利用正弦和余弦函数得到这两个力的大小和方向。
三、力的合成和分解的应用力的合成和分解在物理学中有着广泛的应用。
以下是其中一些常见的应用领域:1. 静力学:力的合成和分解在静力学中经常使用,可以用来解析力的问题以及计算物体的平衡条件。
例如,可以通过力的合成和分解来计算斜面上物体受到的支持力和分解重力的分量。
2. 动力学:在动力学中,力的合成和分解可以帮助我们计算物体的加速度和运动轨迹。
特别是在斜面上滑动和投射运动中,力的合成和分解是解决问题的关键。
力的分解原则和方法

力的分解原则和方法力的分解原则是物理学中的一种基本概念,用于将一个力分解为多个力的合力。
力的分解可以将复杂的力系统简化为更容易处理的问题,是物理学和工程学中常用的方法之一。
力的分解方法主要有平行力分解法和正交力分解法两种。
1.平行力分解法平行力分解法是将一个力分解为平行于特定方向的多个力的合力。
这种方法适用于力矩问题和多体系统问题的求解。
其基本原理是利用平行四边形法则或三角法则将力分解为多个平行的力,然后再计算这些力的合力。
例如,一个斜向上的力F可以被分解为平行于水平方向的力F_x和平行于竖直方向的力F_y。
使用三角法则可以得到F_x = F*cosθ和F_y = F*sinθ。
其中,θ是力F与水平方向的夹角。
2.正交力分解法正交力分解法是将一个力分解为垂直于特定方向的多个力的合力。
这种方法适用于斜面问题和斜坡上物体的自由体图分析。
其基本原理是将力分解为正交或垂直的两个力,一个是垂直于斜面或斜坡的力,另一个是平行于斜面或斜坡的力。
例如,一个斜向上的力F可以被分解为垂直于斜面的力F_n和平行于斜面的力F_t。
使用三角法则可以得到F_n = F*sinθ和F_t =F*cosθ。
其中,θ是力F与斜面的夹角。
力的分解原则还包括力的矢量分解和力的标量分解。
1.力的矢量分解力的矢量分解是将一个力矢量分解为不同方向上的分力矢量的和。
这种方法可以应用于三维空间中力的分解问题。
对于一个力矢量F,可以分解为x轴、y轴和z轴上的分力矢量F_x、F_y和F_z。
例如,一个力矢量F = F_xi + F_yj + F_zk可以分解为F_xi、F_yj和F_zk三个分力矢量的和。
其中,i、j和k是x、y和z轴上的单位矢量。
2.力的标量分解力的标量分解是将一个力分解为标量的和。
这种方法适用于只需要考虑力的大小而不考虑方向时的问题。
对于一个力F,可以分解为x 轴、y轴和z轴上的分力F_x、F_y和F_z。
例如,一个力F可以分解为F_x + F_y + F_z。
力的分解知识点与习题及答案

力的分解基本知识点与练习题基本知识点一、分力的概念1、几个力,如果它们共同产生的效果跟作用在物体上的一个力产生的效果相同,则这几个力就叫做那个力的分力那个力就叫做这几个力的合力;2、分力与合力是等效替代关系,其相同之处是作用效果相同;不同之处是不能同时出现, 在受力分析或有关力的计算中不能重复考虑;二、力的分解1、力的分解的概念:求一个已知力的分力叫做力的分解;2、力的分解是力的合成的逆运算;同样遵守力的平行四边形定则:如果把已知力F作为平行四边形的对角线,那么,与力F共点的平行四边形的两个邻边就表示力F的两个分力F1和F2;3、力的分解的特点是:同一个力,若没有其他限制,可以分解为无数对大小、方向不同的力因为对于同一条对角线.可以作出无数个不同的平行四边形,通常根据力的作用效果分解力才有实际意义;4、按力的效果分解力F的一般方法步骤:1根据物体或结点所处的状态分析力的作用效果2根据力的作用效果,确定两个实际分力的方向;3根据两个分力的方向画出平行四边形;4根据平行四边形定则,利用学过的几何知识求两个分力的大小;也可根据数学知识用计算法;三、对一个已知力进行分解的几种常见的情况和力的分解的定解问题将一个力F分解为两个分力,根据力的平行四边形法则,是以这个力F为平行四边形的一条对角线作一个平行四边形;在无附加条件限制时可作无数个不同的平行四边形;这说明两个力的合力可唯一确定,一个力的两个分力不是唯一的;要确定一个力的两个分力,一定有定解条件;假设合力F一定1、当俩个分力F1已知,求另一个分力F2,如图F2有唯一解;2、当俩个分力F 1, F2的方向已知,求这俩个力,如图F1, F2有唯一解3、当俩个分力F1, F2的大小已知,求解这俩个力;A、当F1F2一组解;B、F1F2,无解;C、F1F2,俩个解;4、当一个分力的方向已知,另一个大小未知;①2sinθ,无解; ②2sinθ,一个解;③2sinFθ,一组解; ④2sinθ,一组解⑤2sinθ为问题的临界条件;5、当一个分力的大小1F已知,求另一个分力2F;①当F1 、F 2时,只有一组解;②当F与2F的夹角先增大后减小, F2一直增大;四、力的正交分解法:1、将一个力沿着两个相互垂直的方向进行分解的方法称为力的正交分解法;力的正交分解法是力学问题中处理力的最常用的方法;2、力的正交分解法的优点:其一,借助数学中的直角坐标系x,y对力进行描述;其二,几何图形关系简单,是直角三角形,解直角三角形方法多,容易求解;3、正交分解的实质:把力的平行四边形合成运算,转化成力的直线运算;4、正交分解的一般步骤:①建立x-O-y直角坐标系②将所有力依次向x轴和y轴上分解为Fx1、Fx2……,Fy1、Fy2……③分别求出x轴和y轴上的合力Fx、Fy④求出合力F,大小F y2 、Fx2 方向Fx、 Fy tan5、正交坐标系的选取原则①把更多的力,放在x轴和y轴上,分解的越少,解题越简单;②把加速度的方向,建立成一个轴,垂直加速度的方向为另一个轴,有时要分解加速度③正交分解的最高目标,使解题简单;复习练习题一、选择题;1.一个力F分解为两个力F1和F2,那么下列说法中错误的是是物体实际受到的力和F2不是物体实际受到的力C.物体同时受到F1、F2和F三个力作用和F2共同作用的效果与F相同2.下列说法中错误的是 A.一个力只能分解成惟一确定的一对分力B.同一个力可以分解为无数对分力 C.已知一个力和它的一个分力,则另一个分力有确定值D.已知一个力和它的两个分力方向,则两分力有确定值3. 已知某力的大小为10 N,则不可能将此力分解为下列哪组力N、3 N N、6 N N、100 N N、400 N4.下列哪一组物理量在运算时遵从平行四边形定则A.位移、速度、加速度、力B.位移、长度、速度、电流C.力、位移、热传递、加速度D.速度、加速度、力、路程5. 在光滑的斜面上自由下滑的物体受到的力是A. 重力和斜面的支持力B. 重力,下滑力和斜面的支持力C. 重力,下滑力D. 重力,支持力,下滑力和正压力6.将一个力分解成两个力,则这两个分力与合力的关系是A.两分力大小之和一定等于合力的大小B.任一分力都一定小于合力C.任一分力都一定大于合力D.任一分力都可能大于、小于或等于合力7.物体在斜面上保持静止状态,下列说法中正确的是①重力可分解为沿斜面向下的力和对斜面的压力②重力沿斜面向下的分力与斜面对物体的静摩擦力是一对平衡力③物体对斜面的压力与斜面对物体的支持力是一对平衡力④重力垂直于斜面方向的分力与斜面对物体的支持力是一对平衡力A.①②B.①③C.②③D.②④ 8.上海南浦大桥,桥面高46m,主桥全长846m,引桥全长7500m,引桥做得这样长的主要目的是A.减小汽车的重力平行于引桥桥面向下的分力B.减小汽车对桥面的压力C.增大汽车的下滑力D.减小汽车的下滑力9.在水平木板上放一个小铁块,逐渐抬高木板一端,在铁块下滑前的过程中,铁块受到的摩擦力F 和铁块对木板的正压力F N 的变化情况是A. F 和F N 都不断增大B. F 增大,F N 减小C. F 减小,F N 增大D. F和F N 都减小10.如图,某同学把放在斜面上的木箱的重力分解为F 1和F 2两个力,F 1平行于斜面向下,F 2垂直于斜面向下,下列关于这两个力的说法中,正确的是A. F 1是木箱受的力B. F 2是斜面受的压力C. F 2是木箱受的力D.斜面受的压力与F 2大小相等11.在图中两个体重相同的小孩静止坐在秋千上,两秋千的绳子是一样的;下面的叙述正确的是A.甲中绳子容易断B.乙中绳子容易断C.甲、乙中绳子一样容易断D.不确定12.用三根轻绳将质量为m 的物块悬挂在空中,如图所示,已知绳ac 和bc 与竖直方向的夹角分别为30o 和60o, A F F G则ac 绳和bc 绳中的拉力分别为 23,21mg 21,23mg 43,21mg 21,43mg 13.三段不可伸长的细绳OA 、OB 、OC 能承受的最大拉力相同,它们共同悬挂一重物,如图所示,其中OB 是水平的,A 端、B 端固定,若逐渐增加C 端所挂物体的质量,则最先断的绳是A.必定是OAB.必定是OBC.必定是OCD.可能是OB ,也可能是OC14.两绳相交,绳与绳、绳与天花板间夹角的大小如图所示,现用一力F 作用于交点A,F 与右绳间的夹角为a ,保持F 的大小不变,改变a 角的大小,忽略绳本身的重力,则下述哪种情况下,两绳所受的拉力相等=150o =135o =120o =90o15.一质量为m 的物体放在水平面上,在与水平面成θ角的力F 的作用下由静止开始运动,物体与水平面间的动摩擦因数为μ,如图所示,则物体所受摩擦力 F f<μmg =μmg >μmg D.不能确定二、填空题;1.复习:力的合成原则:_________________;2.力的分解是_________________的逆运算,它也遵守_________________定则;3.将竖直向下的20N 的力,分解为两个力,其中一个力大小为15N,水平向左,则另一个分力的大小为__________N,方向__________;4.如图,力F=50N 作用于放在水平面上的物体,F 与水平成37°角,如果根据F 的作用效果将它分解成两个力,那么较小的分力F 1=__________N,较大的分力F 2=__________N;要求画出力的分解图,已知sin37°=,cos37°=5.重力为G 的物体放在倾角为α的固定斜面上,现对物块施加一个与斜面垂直的压力F,如图所示,则物体对斜面的压力的大小为__________;6.如图所示,物体静止在光滑水平面上,受到一个水平恒力F 1的作用,要使物体沿OA 方向作直线运动,必须对物体再施加一个力F 2,这个力的最小值为__________; OA 与水平方向的夹角为θ7.已知一个力F=100N,把它分解为两个力,已知其中一个分力F 1与F 的夹角为30°,则另一个分力F 2的最小值为__________N;8.将18N 竖直向下的力,分解为两个分力,其中一个分力沿水平方向且大小为24N,则另一个分力的大小是__________N;三、解答题;1.如图,重力等于G 的球放在倾角为α的斜面上,用一块竖直的板挡住,请根据重力的作用效果分解重力,并计算两分力的大小;2.如图所示,在三角架B 点用一根细绳挂一个50N 的重物G,求横梁AB 和斜梁BC所受的力;3.如图所示,一半径为r 的球重为G,它被长为r 的细绳挂在光滑的竖直墙壁上;求:1细绳拉力的大小;2墙壁受的压力的大小;4.如图所示,两条轻绳AO=BO,A、B两端分别与均质水泥杆的两端固定;现在O点用F=600N的竖直向上的力吊起水泥杆,求在下列两种情况下,力F沿两条绳方向的两个分力的大小:1∠AOB=120°;2∠AOB=90°;5.用两根轻质的绳子AB和BC吊一个0.5kg的灯,如果BC绳处于平,AB绳与水平夹角为60°,求绳AB和BC所受的拉力;g=kg参考答案一、选择题;1. C2. A3. A4. A5. A6. D7. D8. A9. B 10. D 11.B 12. A13. A 14. B 15. A二、填空题;1. 平行四边形定则2. 力的合成;力的平行四边形3. 25;斜向右下,与水平面呈53°角sinθ7. 50 8. 304. 30 ;405. F+Gcosα6. F1三、解答题;1. 水平向左的力,大小为Gtanα;垂直斜面向下的力,大小为G/cosα2. 50√3N;100N3. 12√3G/3 2√3G/34. 1600N 2300√2N5. 98√3/3N; 49√3/3N。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题:力的正交分解法和力的分解的几种常见的情况 一.力的正交分解法
1.定义:将一个力分解为两个相互垂直的分力的方法称为正交分解法。
2.目的:将力的合成化简为同向、反向或垂直方向的分力,便于运用代数运算公式解决矢量的运算,“分解”的目的是为了更好地“合成”。
3.适用情况:适用于计算三个或三个以上的力的合成。
4.步骤:
(1)建立坐标系:以共点力的作用点为坐标原点,直角坐标系x 轴和y 轴的选择应使尽量多的力在坐标轴上。
(2)正交分解各力:将每一个不在坐标轴上的力分解到x 轴和y 轴上,并求出各分力的大小。
(3)分别求出x 轴、y
+++=x x x x F F F F 321… +++=y y y y F F F F 321… (4)求共点力的合力: 合力的大小:22y x F F F +=
,
合力的方向:设F 与x 轴的夹角为α,则tan αx
x
例1.在同一平面上共点的四个力分别为191=F
N 、402=F N 、303=F N 、154=F N ,方向如图所示,求其合力(已知sin37°=0.6,cos37°=0.8)。
解析:
x F 2=2F cos37°=40×0.8=32N x F 3=﹣3F cos37°=﹣30×0.8=﹣24N
则:x F =1F +x F 2+x F 3=19+32+(﹣24)=27N
y F 2=2F sin37°=40×0.6=24N y F 3=3F sin37°=30×0.6=18N
则:y F =y F 2+y F 3+4F =24+18+(﹣15)=27N 则:22722=+=
y x F F F N
合力F 的方向与1F 的夹角为45°斜向上。
二.力的分解的几种常见的情况
1.已知两个分力的方向(在同一直线上的情况除外),有唯一解。
2.已知一个分力的大小和方向,有唯一解。
3.已知两个分力的大小
(1)当1F ≠2F 时,有两解。
(2)1F =2F 时,有唯一解。
F 1F 1F F 2F 1F
2
F
F 平行四边形定则
三角形定则
2F 的方向 2F 的方向 1F 的方向 1F 的方向 F F 2F 1F
F
1F
2F
F
1F
2F
F
1F
2F
F
1F
2F
F
2F
1F
平行四边形定则
平行四边形定则
三角形定则
三角形定则
1F
2F
F
1F
F F
平行四边形定则
三角形定则
1F
F
2F
平行四边形定则
三角形定则
1F
F
2F
以F 2的大 小作圆弧
以F 1的大 小作圆弧
4.已知合力F 、一个分力2F 的方向和另一个分力1F 的大小,求2F 的大小和1F 的方向,有多种情况。
(1)当1F <F sin α时,无解。
(2)当1F =F sin α时,有唯一解。
(3)当F sin α<1F <F 时,有两解。
(4)当1F >F 时,有唯一解。
例2.将力F 分解为两个不为零的力,下列情况具有唯一解的是( AD ) A .已知两个分力的方向,并且不在同一直线上 B .已知一个分力的大小和另一个分力的方向
F
1F
的方向2F 的方向2F F
2F
的方向2F
F
2F 1F
平行四边形定则
三角形定则
的方向2F
2F F
1F
F
2F
1F
的方向2F
平行四边形定则
三角形定则
1F
F
1F
的方向2F
的方向2F 的方向2F
的方向2F
F
F
F
1F
1F
2F
1F
2F 平行四边形定则
三角形定则
F 1F
的方向2F F
的方向2F
2F
1F
F
1F
的方向2 2F
平行四边形定则
三角形定则
C.已知两个分力的大小
D.已知一个分力的大小和方向
简析:A.有唯一解;B.可能无解,可能有唯一解,也可能有两解;C.可能有唯一解,也可能有两解;D.有唯一解。
