Excel指数平滑法案例分析
实验三 用EXCEL进行指数分析

实验三用EXCEL进行指数分析实验目的:用EXCEL进行指数分析实验步骤:指数分析法是研究社会经济现象数量变动情况的一种统计分析法。
指数有总指数与平均指数之分,在这一节我们介绍如何用Excel进行指数分析与因素分析。
一、用Excel计算总指数【例1】:图中是某企业甲、乙、丙三种产品的生产情况,以基期价格p作为同度量因素,计算生产量指数。
如图1图1用EXCEL计算总指数资料及结果计算步骤:第一步:计算各个p0q0:在G2中输入“=C2*D2”,并用鼠标拖曳将公式复制到G2:G4区域。
第二步:计算各个p0*q1:有H2中输入“=C2*F2”,并用鼠标拖曳将公式复制到H2:H4区域。
第三步:计算Σp0q0和Σp0q1:选定G2:G4区域,单击工具栏上的“Σ”按钮,在G5出现该列的求和值。
选定H2:H4区域,单击工具栏上的“Σ”按钮,在H5出现该列的求和值。
第四步:计算生产量综合指数Iq=Σp0q1/Σp0q0:在C6中输入“=H5/G5”便可得到生产量综合指数注意:在输入公式的时候,不要忘记等号,否则就不会出现数值。
二、用Excel计算平均指数现以生产量平均指数为例,说明加权算术平均法的计算方法。
【例2】:图中的A1:A4区域内是某企业生产情况的统计资料,我们要以基期总成本为同度量因素,计算生产量平均指数。
如图2图2用EXCEL计算平均指数资料及结果计算步骤:第一步:计算个体指数k=q1/q0:在F2中输入“=D2/C2”。
并用鼠标拖曳将公式复制到F2:F4区域。
第二步:计算k*p0q0并求和。
在G2中输入“=F2*E2”并用鼠标拖曳将公式复制到G2:G4区域。
选定G2:G4区域,单击工具栏上的:“Σ”按钮,在G5列出现该列的求和值。
第三步:计算生产量平均指数:在C7中输入“=G5/E5”即得到所求的值。
三、用Excel进行因素分析【例3】:我们还用上面的例子,有关资料如图3图3用EXCEL进行因素分析资料及结果进行因素分析的计算步骤如下:第一步:计算各个p0*q0和∑p0q0:在G2中输入“C2*D2”,并用鼠标拖曳将公式复制到G2:G4区域。
Excel指数平滑法案例分析

Excel应用案例指数平滑法移动平均法的预测值实质上是以前观测值的加权和,且对不同时期的数据给予相同的加权。
这往往不符合实际情况。
指数平滑法则对移动平均法进行了改进和发展,其应用较为广泛。
1. 指数平滑法的基本理论根据平滑次数不同,指数平滑法分为:一次指数平滑法、二次指数平滑法和三次指数平滑法等。
但它们的基本思想都是:预测值是以前观测值的加权和,且对不同的数据给予不同的权,新数据给较大的权,旧数据给较小的权。
①一次指数平滑法设时间序列为,则一次指数平滑公式为:式中为第 t周期的一次指数平滑值;为加权系数,0<<1。
为了弄清指数平滑的实质,将上述公式依次展开,可得:由于0<<1,当→∞时,→0,于是上述公式变为:由此可见实际上是的加权平均。
加权系数分别为,,…,是按几何级数衰减的,愈近的数据,权数愈大,愈远的数据,权数愈小,且权数之和等于1,即。
因为加权系数符合指数规律,且又具有平滑数据的功能,所以称为指数平滑。
用上述平滑值进行预测,就是一次指数平滑法。
其预测模型为:即以第t周期的一次指数平滑值作为第t+1期的预测值。
②二次指数平滑法当时间序列没有明显的趋势变动时,使用第t周期一次指数平滑就能直接预测第t+1期之值。
但当时间序列的变动出现直线趋势时,用一次指数平滑法来预测仍存在着明显的滞后偏差。
因此,也需要进行修正。
修正的方法也是在一次指数平滑的基础上再作二次指数平滑,利用滞后偏差的规律找出曲线的发展方向和发展趋势,然后建立直线趋势预测模型。
故称为二次指数平滑法。
设一次指数平滑为,则二次指数平滑的计算公式为:若时间序列从某时期开始具有直线趋势,且认为未来时期亦按此直线趋势变化,则与趋势移动平均类似,可用如下的直线趋势模型来预测。
式中t为当前时期数;T为由当前时期数t到预测期的时期数;为第t+T期的预测值;为截距,为斜率,其计算公式为:③三次指数平滑法若时间序列的变动呈现出二次曲线趋势,则需要用三次指数平滑法。
Excel变量与三次指数平滑模拟预测方法

#在 XB 单元格中输入 (1""$: M 4;< ""8$:R4GB<:RKB,&B8 ) # 选 取 XB 单 元 格 # 拖 动 填 充 柄 至 X:@ 单元格 $
则完成了三次指数平滑参数 Y’%-’%T’ 计算公式的输入 ’ ! 下转第 ;:Z 页 "
FGK1
NIJK1 ; !OJKLO ’
! 指标含义是否可比 $ 如国民收入
易与国民总收入混淆 $ 前者是五大物质 生产部门的净产值之和 # 是改革开放前 反映经济总量的主要指标 ’ 后者即过去 所称的国民生产总值 $ 两者指标含义 ( 口 径 ( 及计算方法是完全不同的 $
’ 数据是否经过修正 $ 统计既然是
对社会经济发展变化的一种事后反映# 随着基础数据的不断完善 # 或者计算方 法和分类标准发生了变化 # 就有必要对 一些数据进行修正 # 不仅是当年和上年 数据 # 而且要对历史数据进行调整 # 这是 统计上的国际惯例 $ 如美国季度国内生 产总值及其增长率 # 一般季后 #( 天公布 预 测 数 据 # 季 后 *( 天 公 布 初 步 统 计 数 据 # 季后 E( 天公布初修正统计数据 $ 所 以利用统计资料时 # 必须以最新修正的 数据为准 $ ! 作者单位 : 浙江工商大学统计学院 "
! 在 运 算 表 !44 " 中 # 选 取 ’()’/2 区
域 # 并单击复制 ’
! 作者单位 : 江苏常熟理工学院 "
! 责任编辑 : 亦 民"
!"#
统计与决策
万方数据
Excel变量与三次指数平滑模拟预测方法
作者: 作者单位: 刊名: 英文刊名: 年,卷(期): 引用次数: 丁沧海 江苏常熟理工学院 统计与决策 STATISTICS AND DECISION 2005,(11) 1次
利用Excel进行指数平滑分析

利用Excel进行指数平滑分析与预测(2)【例】连续10年的灌溉面积。
第一步,录入数据(图1)。
图1 原始数据第二步,选项设置。
沿着主菜单的“工具(T)→数据分析(D)”路径打开“数据分析”选项框,选中“指数平滑”(图2)。
图2 数据分析选项框与“指数平滑”的位置确定以后,弹出移动平均对话框(图3),然后按如下步骤进行设置:⒈将光标置入“输入区域”对应的空白栏,然后用鼠标从B1到B11选中全部时间序列连同标志;⒉选中“标志”(位于第一行);⒊在“阻尼系数”对应的空白栏中键入“0.9”,表示指数平滑系数为0.1(即取α=0.1。
注意:指数平滑系数与阻尼系数的关系是“平滑系数+阻尼系数=1”);⒋将光标置入“输出区域”对应的空白栏,选中从C2到C11的单元格,作为计算结果的输出位置;⒌选中“图表输出”和“标准误差”,这样会自动生成移动平均坐标图和标准误差值。
注意:如果“输入区域”对应的空白栏设置为“$B$2:$B$11”,即不包括数据标志项,则不要选中“标志”(图4)。
图3 指数平滑选项框(包括数据标志)图3 指数平滑选项框(不包括数据标志)第三步,输出结果。
完成上述设置以后,确定,即可得到计算结果,包括指数平滑结果及其标准误差(图5),以及指数平滑曲线图(图6)。
图5 移动平均结果:平滑系数为α=0.1图6 阻尼系数为0.9(平滑系数为0.1)的移动平均预测曲线(水红色)如果不借助E x cel 的“数据分析”工具,指数平滑计算也是非常简单的,有关计算方法在“利用Exc el 进行指数平滑分析与预测(1)”中已经详细说明,不赘述,下面只介绍标准误差的计算方法。
与移动平均法的标准误差计算类似,我们有两种途径。
计算方法之一:利用平方根命令sqr t 和计算两个数组相对数值误差的平方和命令sumxm y 2。
指数平滑实训操作过程

第十章综合实训
目标:
1.用EXCEL 表进行一次指数平滑预测。
内容与要求:
1. 按班级每1人为一组,用下列资料,用EXCEL 进行一次指数平滑预测。
平滑系数α=0.5,=∧
1y 8。
ABC 公司销售额资料表
形成过程截图和最终成果截图上交。
成果与检测:
“实训过程考核”(按过程截图)与 “实训结果考核”(按最终成果截图)结合。
(参考答案
1. 将数据输入EXCEL 表,点击工具,并点加载宏,选分析工具库,并点确定(如参考图10-1EXCEL 截图1所示)。
参考图10-1EXCEL截图1
2点击工具,并点击数据分析,选指数平滑(如参考图10-2EXCEL截图2所示)
参考图10-2EXCEL截图2
再确定
3输入区域选B2:B14,阻尼系数选0.5,输出区域选C2:C14,并勾选图表输出(如参考图10-3EXCEL截图3所示)
参考图10-3EXCEL截图3
4点击确定,可得预测值(如参考图10-4EXCEL截图4所示)
参考图10-4EXCEL截图4)。
指数平滑法 实例

指数平滑法实例?
答:指数平滑法是一种常用的时间序列预测方法,可以用于预测未来的销售、需求等。
以下是两个指数平滑法的应用实例:
实例一:某软件公司的销售预测
某软件公司A给出了2000-2005年的历史销售资料。
根据经验判断法,A公司2000-2005年销售额时间序列波动很大,长期趋势变化幅度较大,呈现明显且迅速的上升趋势,宜选择较大的α值,可在0.5-0.8间选值,以使预测模型灵敏度高些。
经过第一次指数平滑后,数列呈现直线趋势,故选用二次指数平滑法即可。
试算结果后,得到了预测模型,可以用于预测2006年的销售额。
实例二:某地财政收入预测
已知某地1983年至1993年的财政收入数据,试用指数平滑法求解趋势直线方程并预测1996年的财政收入。
通过分析工具和计算,得到了趋势线预测模型,从而可以计算出1996年的财政收入预测值。
以上两个实例仅供参考,指数平滑法的应用非常广泛,可以根据不同的数据和需求进行灵活应用。
指数平滑法应用案例

Excel应用案例指数平滑法移动平均法的预测值实质上是以前观测值的加权和,且对不同时期的数据给予相同的加权。
这往往不符合实际情况。
指数平滑法则对移动平均法进行了改进和发展,其应用较为广泛。
1. 指数平滑法的基本理论根据平滑次数不同,指数平滑法分为:一次指数平滑法、二次指数平滑法和三次指数平滑法等。
但它们的基本思想都是:预测值是以前观测值的加权和,且对不同的数据给予不同的权,新数据给较大的权,旧数据给较小的权。
①一次指数平滑法设时间序列为,则一次指数平滑公式为:式中为第 t周期的一次指数平滑值;为加权系数,0<<1。
为了弄清指数平滑的实质,将上述公式依次展开,可得:由于0<<1,当→∞时,→0,于是上述公式变为:由此可见实际上是的加权平均。
加权系数分别为,,…,是按几何级数衰减的,愈近的数据,权数愈大,愈远的数据,权数愈小,且权数之和等于1,即。
因为加权系数符合指数规律,且又具有平滑数据的功能,所以称为指数平滑。
用上述平滑值进行预测,就是一次指数平滑法。
其预测模型为:即以第t周期的一次指数平滑值作为第t+1期的预测值。
②二次指数平滑法当时间序列没有明显的趋势变动时,使用第t周期一次指数平滑就能直接预测第t+1期之值。
但当时间序列的变动出现直线趋势时,用一次指数平滑法来预测仍存在着明显的滞后偏差。
因此,也需要进行修正。
修正的方法也是在一次指数平滑的基础上再作二次指数平滑,利用滞后偏差的规律找出曲线的发展方向和发展趋势,然后建立直线趋势预测模型。
故称为二次指数平滑法。
设一次指数平滑为,则二次指数平滑的计算公式为:若时间序列从某时期开始具有直线趋势,且认为未来时期亦按此直线趋势变化,则与趋势移动平均类似,可用如下的直线趋势模型来预测。
式中t为当前时期数;T为由当前时期数t到预测期的时期数;为第t+T期的预测值;为截距,为斜率,其计算公式为:③三次指数平滑法若时间序列的变动呈现出二次曲线趋势,则需要用三次指数平滑法。
使用excel计算指数平滑和移动平均
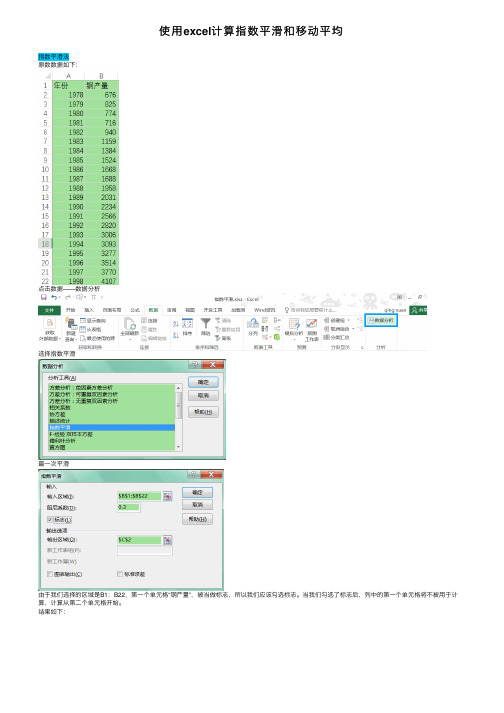
使⽤excel计算指数平滑和移动平均
指数平滑法
原数数据如下:
点击数据——数据分析
选择指数平滑
最⼀次平滑
由于我们选择的区域是B1:B22,第⼀个单元格“钢产量”,被当做标志,所以我们应该勾选标志。
当我们勾选了标志后,列中的第⼀个单元格将不被⽤于计算,计算从第⼆个单元格开始。
结果如下:
做⼆次平滑
这⾥,我们不再采⽤标志,所以数据区间选择在C3:C22
对⽐⼀下
阻尼系数=0.3
阻尼系数=0.05
阻尼系数=0.9
画在⼀张图上对⽐下,可见阻尼系数越⼤,曲线越平。
移动平均(⼀阶和⼆阶)
同理可以使⽤excel计算得到如下表:
相关数据⽂件:附件列表。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Excel应用案例
指数平滑法
移动平均法的预测值实质上是以前观测值的加权和,且对不同时期的数据给予相同的加权。
这往往不符合实际情况。
指数平滑法则对移动平均法进行了改进和发展,其应用较为广泛。
1. 指数平滑法的基本理论
根据平滑次数不同,指数平滑法分为:一次指数平滑法、二次指数平滑法和三次指数平滑法等。
但它们的基本思想都是:预测值是以前观测值的加权和,且对不同的数据给予不同的权,新数据给较大的权,旧数据给较小的权。
①一次指数平滑法
设时间序列为,则一次指数平滑公式为:
式中为第 t周期的一次指数平滑值;为加权系数,0<<1。
为了弄清指数平滑的实质,将上述公式依次展开,可得:
由于0<<1,当→∞时,→0,于是上述公式变为:
由此可见实际上是的加权平均。
加权系数分别为,
,…,是按几何级数衰减的,愈近的数据,权数愈大,愈远的数据,
权数愈小,且权数之和等于1,即。
因为加权系数符合指数规律,且又具有平滑数据的功能,所以称为指数平滑。
用上述平滑值进行预测,就是一次指数平滑法。
其预测模型为:
即以第t周期的一次指数平滑值作为第t+1期的预测值。
②二次指数平滑法
当时间序列没有明显的趋势变动时,使用第t周期一次指数平滑就能直接预测第t+1
期之值。
但当时间序列的变动出现直线趋势时,用一次指数平滑法来预测仍存在着明显的滞后偏差。
因此,也需要进行修正。
修正的方法也是在一次指数平滑的基础上再作二次指数平滑,利用滞后偏差的规律找出曲线的发展方向和发展趋势,然后建立直线趋势预测模型。
故称为二次指数平滑法。
设一次指数平滑为,则二次指数平滑的计算公式为:
若时间序列从某时期开始具有直线趋势,且认为未来时期亦按此直
线趋势变化,则与趋势移动平均类似,可用如下的直线趋势模型来预测。
式中t为当前时期数;T为由当前时期数t到预测期的时期数;为第t+T期的预
测值;为截距,为斜率,其计算公式为:
③三次指数平滑法
若时间序列的变动呈现出二次曲线趋势,则需要用三次指数平滑法。
三次指数平滑是在二次指数平滑的基础上再进行一次平滑,其计算公式为:
三次指数平滑法的预测模型为:
其中:
④加权系数的选择
在指数平滑法中,预测成功的关键是的选择。
的大小规定了在新预测值中新数据和原预测值所占的比例。
值愈大,新数据所占的比重就愈大,原预测值所占比重就愈小,反之亦然。
若把一次指数平滑法的预测公式改写为:
则从上式可以看出,新预测值是根据预测误差对原预测值进行修正得到的。
的大小表明了修正的幅度。
值愈大,修正的幅度愈大,值愈小,修正的幅度愈小。
因此,值既代表了预测模型对时间序列数据变化的反应速度,又体现了预测模型修匀误差的能力。
在实际应用中,值是根据时间序列的变化特性来选取的。
若时间序列的波动不大,比较平稳,则应取小一些,如0.1~0.3;若时间序列具有迅速且明显的变动倾向,则应取大一些,如0.6~0.9。
实质上,是一个经验数据,通过多个值进行试算比较而定,哪个值引起的预测误差小,就采用哪个。
2. 应用举例
已知某厂1978~1998年的钢产量如下表所示,试预测1999年该厂的钢产量。
下面利用
选择工具菜单中的数据分析命令,此时弹出数据分析对话框。
在分析工具列表框中,选择指数平滑工具。
这时将出现指数平滑对话框,如图8-4所示。
图8-4
在输入框中指定输入参数。
在输入区域指定数据所在的单元格区域B1:B22;因指定的输入区域包含标志行,所以选中标志复选框;在阻尼系数指定加权系数0.3。
在输出选项框中指定输出选项。
本例选择输出区域,并指定输出到当前工作表以C2为左上角的单元格区域;选中图表输出复选框。
单击确定按钮。
这时,Excel给出一次指数平滑值,如图8-5所示。
图8-5 从图8-5可以看出,钢产量具有明显的线性增长趋势。
因此需使用二次指数平滑法,即在一次指数平滑
的基础上再进行指数平滑。
所得结果如图8-6所示。
图8-6
利用前面的截距和斜率计算公式可得:
于是,可得钢产量的直线趋势预测模型为:
预测1999年的钢产量为:。
