必修5 正余弦定理资料整理
高中数学必修五知识点大全

知识点串讲必修五第一章:解三角形1.1.1正弦定理1、正弦定理:在一个三角形中,各边和它所对角的正弦的比相等,即sin sin abA B =sin cC =一般地,已知三角形的某些边和角,求其他的边和角的过程叫作解三角形。
2、已知∆ABC 中,∠A 060=,a =求sin sin sin a b c A B C++++ 证明出sin sin a b A B =sin c C ==sin sin sin a b c A B C++++ 解:设sin sin a b A B =(>o)sin c k k C== 则有sin a k A =,sin b k B =,sin c k C = 从而sin sin sin a b c A B C ++++=sin sin sin sin sin sin k A k B k C A B C++++=k又sin a A =2k ==,所以sin sin sin a b c A B C++++=2 评述:在∆ABC 中,等式sin sin a b A B =sin c C ==()0sin sin sin a b c k k A B C ++=>++ 恒成立。
3、已知∆ABC 中,sin :sin :sin 1:2:3A B C =,求::a b c(答案:1:2:3)1.1.2余弦定理1、余弦定理:三角形中任何一边的平方等于其他两边的平方的和减去这两边与它们的夹角的余弦的积的两倍.即 2222cos a b c bc A =+-2222cos b a c ac B =+-2222cos c a b ab C =+-从余弦定理,又可得到以下推论:222cos 2+-=b c a A bc 222cos 2+-=a c b B ac 222cos 2+-=b a c C ba2、在∆ABC 中,已知=a c 060=B ,求b 及A⑴解:∵2222cos =+-b a c ac B=222+-⋅cos 045=2121)+-=8∴=b求A 可以利用余弦定理,也可以利用正弦定理:⑵解法一:∵cos 2222221,22+-=b c a A bc ∴060.=A解法二:∵sin 0sin sin45,=a A B b2.4 1.43.8,+=21.8 3.6,⨯=∴a <c ,即00<A <090,∴060.=A评述:解法二应注意确定A 的取值范围。
必修五正弦定理和余弦定理

必修五第一讲 正弦定理知识梳理1.正弦定理:在一个三角形中,各边和它所对角的正弦的比相等,即a sin A =b sin B =csin C.2.解三角形:一般地,把三角形的三个角A 、B 、C 和它们的对边a 、b 、c 叫做三角形的元素,已知三角形的几个元素求其他元素的过程叫做解三角形.题型分析[例1] 在△ABC 中,已知a [解] A =180°-(B +C )=180°-(60°+75°)=45°.由b sin B =a sin A 得,b =a sin B sin A =8×sin 60°sin 45°=46,由a sin A =c sin C得,c =a sin C sin A =8×sin 75°sin 45°=8×2+6422=4(3+1).∴A =45°,b =46,c =4(3+1). [变式训练]在△ABC 中,已知c =10,A =45°,C =30°,解这个三角形. 解:∵A =45°,C =30°,∴B =180°-(A +C )=105°.由a sin A =c sin C 得a =c sin A sin C =10×sin 45°sin 30°=10 2. 由b sin B =c sin C 得b =c sin B sin C =10×sin 105°sin 30°=20sin 75°,∵sin 75°=sin (30°+45°)=sin 30°cos 45°+cos 30°sin 45° =2+64,∴b =20×2+64=52+5 6.[例2] 在△ABC [解] ∵a sin A =c sin C ,∴sin C =c sin Aa =6×sin 45°2=32,∴C =60°或C =120°.当C =60°时,B =75°,b =c sin B sin C =6sin 75°sin 60°=3+1; 当C =120°时,B =15°,b =c sin B sin C =6sin 15°sin 120°=3-1. ∴b =3+1,B =75°,C =60°或b =3-1,B =15°,C =120°. [变式训练]在△ABC 中,若c =6,C =π3,a =2,求A ,B ,b .解:由a sin A =c sin C ,得sin A =a sin C c =22.∴A =π4或A =34π.又∵c >a ,∴C >A ,∴只能取A =π4, ∴B =π-π3-π4=5π12,b =c sin Bsin C=6·sin 5π12sinπ3=3+1.[例3] 在△ABC 中,sin 2 A =sin 2 B +sin 2 C ,且sin A =2sin B ·cos C .试判断△ABC 的形状.[解] 由正弦定理,得sin A =a 2R ,sin B =b 2R ,sin C =c2R.∵sin 2 A =sin 2 B +sin 2 C ,∴⎝⎛⎭⎫a 2R 2=⎝⎛⎭⎫b 2R 2+⎝⎛⎭⎫c 2R 2, 即a 2=b 2+c 2,故A =90°.∴C =90°-B ,cos C =sin B .∴2sin B ·cos C =2sin 2 B =sin A =1. ∴sin B =22.∴B =45°或B =135°(A +B =225°>180°,故舍去).∴△ABC 是等腰直角三角形. [变式训练]在△ABC 中,若b =a cos C ,试判断该三角形的形状.解:∵b =a cos C ,a sin A =bsin B=2R .(2R 为△ABC 外接圆直径)∴sin B =sin A ·cos C .∵B =π-(A +C ),∴sin (A +C )=sin A ·cos C .即sin A cos C +cos A sin C =sin A ·cos C , ∴cos A sin C =0,∵A 、C ∈(0,π),∴cos A =0,∴A =π2,∴△ABC 为直角三角形.[随堂检测]1.(2012·广东高考)在△ABC 中,若∠A =60°,∠B =45°,BC =32,则AC =( )A .43B .2 3 C. 3D.32解析:选B 由正弦定理得:BC sin A =AC sin B ,即32sin 60°=AC sin 45°,所以AC =3232×22=23,故选B.2.在△ABC 中,a =5,b =3,C =120°,则sin A ∶sin B 的值是( A )A.53B.35C.37D.573.在△ABC 中,若(sin A +sin B )(sin A -sin B )=sin 2 C ,则△ABC 是________三角形. 解析:由已知得sin 2 A -sin 2 B =sin 2 C ,根据正弦定理知sin A =a 2R ,sin B =b 2R ,sin C =c2R,所以⎝⎛⎭⎫a 2R 2-⎝⎛⎭⎫b 2R 2=⎝⎛⎭⎫c 2R 2,即a 2-b 2=c 2,故b 2+c 2=a 2.所以△ABC 是直角三角形.答案:直角 4.(2012·北京高考)在△ABC 中,若a =3,b =3,∠A =π3,则∠C 的大小为________.解析:由正弦定理可知sin B =b sin Aa =3sin π33=12,所以∠B =π6或5π6(舍去),所以∠C =π-∠A -∠B =π-π3-π6=π2. 5.不解三角形,判断下列三角形解的个数.(1)a =5,b =4,A =120°; (2)a =7,b =14,A =150°; (3)a =9,b =10,A =60°. 解:(1)sin B =b sin 120°a =45×32<32,所以△ABC 有一解.(2)sin B =b sin 150°a=1,所以△ABC 无解.(3)sin B =b sin 60°a =109×32=539,而32<539<1,所以当B 为锐角时,满足sin B =539的B 的取值范围为60°<B <90°.当B 为钝角时,有90°<B <120°,也满足A +B <180°,所以△ABC 有两解.课后作业一、选择题1.在△ABC 中,下列式子与sin A a的值相等的是( )A.b cB.sin B sin AC.sin C cD.csin C解析:选C 由正弦定理得a sin A =c sin C ,所以sin A a =sin Cc. 2.(2013·浏阳高二检测)在△ABC 中,若sin A >sin B ,则A 与B 的大小关系为( )A .A >B B .A <BC .A ≥BD .A 、B 的大小关系不确定解析:选A ∵sin A >sin B ,∴2R sin A >2R sin B ,即a >b ,故A >B .3.一个三角形的两个角分别等于120°和45°,若45°角所对的边长是46,那么120°角所对边长是( )A .4B.12 3 C .4 3D .12解析:选D 若设120°角所对的边长为x ,则由正弦定理可得:x sin 120°=46sin 45°,于是x =46·sin 120°sin 45°=46×3222=12,故选D.4.△ABC 的三个内角A ,B ,C 所对的边分别为a ,b ,c ,a sin A sin B +b cos 2A =2a ,则ba=( )A .2 3B.2 2C.3D. 2解析:选D 由正弦定理,得sin 2A sin B +sin B cos 2A =2sin A ,即sin B ·(sin 2A +cos 2A )=2sin A .所以sin B =2sin A .∴b a =sin Bsin A= 2.5.以下关于正弦定理或其变形的叙述错误的是( )A .在△ABC 中,a ∶b ∶c =sin A ∶sinB ∶sinC B .在△ABC 中,若sin 2A =sin 2B ,则a =bC .在△ABC 中,若sin A >sin B ,则A >B ,若A >B ,则sin A >sin B 都成立D .在△ABC 中,asin A =b +c sin B +sin C解析:选B 由正弦定理易知A ,C ,D 正确.对于B ,由sin 2A =sin 2B ,可得A =B ,或2A +2B =π,即A =B ,或A +B =π2,∴a =b ,或a 2+b 2=c 2,故B 错误.二、填空题6.在△ABC 中,若a =14,b =76,B =60°,则C =________.解析:由正弦定理知a sin A =b sin B ,又a =14,b =76,B =60°,∴sin A =a sin B b =14sin 60°76=22,∵a <b ,∴A <B ,∴A =45°,∴C =180°-(B +A )=180°-(60°+45°)=75°.答案:75° 7.在△ABC 中,B =30°,C =120°,则a ∶b ∶c =________.解析:A =180°-B -C =30°,由正弦定理得a ∶b ∶c =sin A ∶sin B ∶sin C ,即a ∶b ∶c =sin 30°∶sin 30°∶sin 120°=1∶1∶ 3.答案:1∶1∶ 38.在△ABC 中,若A =120°,AB =5,BC =7,则sin B =________.解析:由正弦定理,得sin C =AB ·sin A BC =5sin 120°7=5314.可知C 为锐角,∴cos C =1-sin 2C =1114.∴sin B =sin(180°-120°-C )=sin(60°-C )=sin 60°·cos C -cos 60°·sin C =3314.答案:3314三、解答题9.(2011·安徽高考)在△ABC 中,a ,b ,c 分别为内角A ,B ,C 所对的边长,a =3,b =2,1+2cos(B +C )=0,求边BC 上的高.解:由1+2cos(B +C )=0和B +C =π-A ,得1-2cos A =0,所以cos A =12,sin A =32.再由正弦定理,得sin B =b sin A a =22.由b <a 知B <A ,所以B 不是最大角,B <π2,从而cos B =1-sin 2B =22.由上述结果知sin C =sin(A +B )=22×(32+12)=6+24. 设边BC 上的高为h ,则有h =b sin C =3+12. 10.在△ABC 中,已知a 2sin B cos B =b 2sin Acos A,试数列△ABC 的形状.解:∵a 2sin B cos B =b 2sin A cos A ,a =2R sin A ,b =2R sin B ,∴4R 2sin 2 A sin B cos B =4R 2sin 2 B sin Acos A.又∵sin A sin B ≠0,∴sin A cos A =sin B cos B ,即sin 2A =sin 2B ,∴2A =2B ,或2A +2B =π,即A =B ,或A +B =π2.故△ABC 是等腰三角形或直角三角形.必修五第二讲 余弦定理知识梳理 余弦定理题型分析[例1] 在△ABC 中,若a [解] 由于a ∶b ∶c =1∶3∶2,可设a =x ,b =3x ,c =2x .由余弦定理的推论,得cos A =b 2+c 2-a 22bc =3x 2+4x 2-x 22×3x ×2x =32,故A =30°.同理可求得cos B =12,cos C =0,所以B =60°,C =90°.[变式训练]边长为5,7,8的三角形中,最大角与最小角的和是________.解析:设中间角为θ,由于8>7>5,故θ的对边的长为7,由余弦定理,得cos θ=52+82-722×5×8=12.所以θ=60°,故另外两角和为180°-60°=120°.答案:120°[例2] 在△ABC [解] 由余弦定理得:b 2=a 2+c 2-2ac cos B =82+[4(3+1)]2-2×8×4(3+1)·cos 60°=64+16(4+23)-64(3+1)×12=96,∴b =4 6.法一:由cos A =b 2+c 2-a 22bc =96+16(3+1)2-642×46×4(3+1)=22,∵0°<A <180°,∴A =45°.故C =180°-A -B =180°-45°-60°=75°.法二:由正弦定理a sin A =b sin B ,∴8sin A =46sin 60°,∴sin A =22,∵b >a ,c >a ,∴a 最小,即A 为锐角.因此A =45°.故C =180°-A -B =180°-45°-60°=75°. [变式训练]在△ABC ,已知a =22,b =23,C =15°,解此三角形.解:c 2=a 2+b 2-2ab cos C =(22)2+(23)2-2×22×23×cos(45°-30°)=8-43=(6-2) 2∴c =6- 2. 法一:由余弦定理的推论得cos A =b 2+c 2-a 22bc =(23)2+(6-2)2-(22)22×23×(6-2)=22.∵0°<A <180°,∴A =45°,从而B =120°.法二:由正弦定理得sin A =a sin C c =22×6-246-2=22.∵a <b ,∴A <B ,又0°<A <180°,∴A 必为锐角,∴A =45°,从而得B =120°.[例3] 在△[解] 法一:由余弦定理b 2=a 2+c 2-2ac cos B ,得32=a 2+(33)2-2a ×33×cos 30∴a 2-9a +18=0,得a =3或6.当a =3时,A =30°,∴C =120°.当a =6时,由正弦定理得sin A =a sin Bb =6×123=1.∴A =90°,∴C =60°.法二:由b <c ,B =30°,b >c sin 30°=33×12=332知本题有两解.由正弦定理得sin C =c sin Bb =33×123=32, ∴C =60°或120°,当C =60°时,A =90°,△ABC 为直角三角形.由勾股定理得a =b 2+c 2=32+(33)2=6,当C =120°时,A =30°,△ABC 为等腰三角形,∴a =3.[变式训练]已知:在△ABC 中,cos A =35,a =4,b =3,则c =________.解析:A 为b ,c 的夹角,由余弦定理得a 2=b 2+c 2-2bc cos A ,∴16=9+c 2-6×35c ,整理得5c 2-18c -35=0.解得c =5或c =-75(舍).答案:5[例4] 在△ABC 中,若a cos A [解] 由余弦定理可得a ·b 2+c 2-a 22bc +b ·a 2+c 2-b 22ac =c ·a 2+b 2-c 22ab等式两边同乘以2abc 得a 2(b 2+c 2-a 2)+b 2(a 2+c 2-b 2)=c 2(a 2+b 2-c 2),整理化简得a 4+b 4-2a 2b 2=c 4,∴(a 2-b 2)2=c 4.因此有a 2-b 2=c 2或b 2-a 2=c 2.即a 2=b 2+c 2或b 2=a 2+c 2故△ABC 为直角三角形. [变式训练].在△ABC 中,若cos A =sin Bsin C,试判断其形状.解:由cos A =sin B sin C 得cos A =bc ,即b 2+c 2-a 22bc =b c,∴b 2+c 2-a 2=2b 2,即a 2+b 2=c 2,因此△ABC 是以C 为直角的直角三角形.[例5]如图所示,在四边形ABCD 中,AD ⊥CD ,AD =10,AB =14,∠BDA =60°,∠BCD =135°,求出BC 的长. [解]设BD =x .在△ABD 中,根据余弦定理,AB 2=AD 2+BD 2-2AD ·BD cos ∠BDA ,∴142=102+x 2-2×10×x cos60°,即x 2-10x -96=0,解得x 1=16,x 2=-6(舍去),∴BD =16.∵AD ⊥CD ,∠BDA =60°,∴∠CDB =30°.在△BCD 中,由正弦定理,BC sin ∠CDB =BDsin ∠BCD,∴BC =16sin 30°sin 135°=8 2.注:将四边形ABCD 分解为两个△ABD 和△BCD ,利用余弦定理列出关于x 的一元二次方程,化简方程时易出错,应注意步骤及计算的准确性. 由AD ⊥CD ,∠BDA =60°得∠CDB =30°,学生有时不易想到. [变式训练]如图所示,在△ABC 中,已知B =45°,D 是BC 边上一点,AD =5,AC =7,DC =3,求AB . 解:在△ADC 中,cos C =AC 2+DC 2-AD 22·AC ·DC =72+32-522×7×3=1114.又∵0°<C <180°,∴sin C =5314.在△ABC 中,AC sin B =AB sin C ,∴AB =sin C sin B ·AC =5314·2·7=562. [随堂注册]1.在△ABC 中,已知A =30°,且3a =3b =12,则c 的值为( C )A .4B .8C .4或8D .无解2.在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,若c 2-a 2-b 22ab>0,则△ABC ( C )A .一定是锐角三角形 B.一定是直角三角形 C .一定是钝角三角形 D .是锐角或直角三角形3.(2012·陕西高考)在△ABC 中,角A ,B ,C 所对边的长分别为a ,b ,c .若a =2,B =π6,c =23,则b =________.解析:由余弦定理得b 2=a 2+c 2-2ac cos B =4+12-2×2×23×32=4,所以b =2.答案:2 4.在△ABC 中,已知a =7,b =3,c =5,则最大的角是________.解析:∵a >c >b ,∴A 为最大角.cos A =b 2+c 2-a 22bc =32+52-722×3×5=-12,又∵0°<A <180°,∴A =120°.答案:120°5.在△ABC 中,已知a =5,b =3,角C 的余弦值是方程5x 2+7x -6=0的根,求第三边c 的长.解:5x 2+7x -6=0可化为(5x -3)(x +2)=0.∴x 1=35,x 2=-2(舍去).∴cos C =35.根据余弦定理,c 2=a 2+b 2-2ab cos C =52+32-2×5×3×35=16∴c =4,即第三边长为4.课后作业一、选择题1.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若A =π3,a =3,b =1,则c =( B )A .1B.2C.3-1D. 32.在△ABC 中,若a =8,b =7,cos C =1314,则最大角的余弦值是( )A .-15B.-16 C .-17 D .-18解析:选C 由余弦定理,得c 2=a 2+b 2-2ab cos C =82+72-2×8×7×1314=9,所以c =3,故a 最大,所以最大角的余弦值为cos A =b 2+c 2-a 22bc =72+32-822×7×3=-17.3.在△ABC 中,B =60°,b 2=ac ,则此三角形一定是( B )A .直角三角形 B.等边三角形 C .等腰直角三角形 D .钝角三角形4.(2013·宁阳高二检测)在△ABC 中,b cos A =a cos B ,则△ABC 是( )A .等边三角形B.等腰三角形 C .直角三角形 D .锐角三角形解析:选B 因为b cos A =a cos B ,所以b ·b 2+c 2-a 22bc =a ·a 2+c 2-b 22ac.所以b 2+c 2-a 2=a 2+c 2-b 2.所以a 2=b 2.所以a =b .故此三角形是等腰三角形.5.在△ABC 中,B =60°,最大边与最小边之比为(3+1)∶2,则最大角为( )A .45°B.60° C .75° D .90°解析:选C 由题意可知c <b <a ,或a <b <c ,不妨设c =2x ,则a =(3+1)x ,∴cos B =a 2+c 2-b 22ac.即12=(3+1)2x 2+4x 2-b 22·(3+1)x ·2x ∴b 2=6x 2.∴cos C =a 2+b 2-c 22ab =(3+1)2x 2+6x 2-4x 22(3+1)x ·6x=22,∴C =45°, ∴A =180°-60°-45°=75°. 二、填空题6.(2012·湖北高考)设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c .若(a +b -c )(a +b +c )=ab ,则角C =________解析:∵(a +b )2-c 2=ab ,∴cos C =a 2+b 2-c 22ab =-12,C =2π3.答案:2π37.在△ABC 中,A =120°,AB =5,BC =7,则sin Bsin C的值为________.解析:由余弦定理可得49=AC 2+25-2×5×AC ×cos 120°,整理得:AC 2+5·AC -24=0,解得AC =3或AC =-8(舍去),再由正弦定理可得sin B sin C =AC AB =35.答案:358.在△ABC 中,若sin A ∶sin B ∶sin C =3∶5∶7,则C 的大小是________.解析:因为sin A ∶sin B ∶sin C =3∶5∶7,由正弦定理可得a ∶b ∶c =3∶5∶7,设a =3k (k >0),则b =5k ,c =7k ,由余弦定理的推论得cos C =a 2+b 2-c 22ab =-12,又0°<C <180°,所以C =120°.答案:120°三、解答题9.在△ABC 中,若已知(a +b +c )(a +b -c )=3ab ,并且sin C =2sin B cos A ,试判断△ABC 的形状. 解:由正弦定理,可得sin B =b 2R ,sin C =c2R .由余弦定理,得cos A =b 2+c 2-a 22bc.代入sin C =2sin B cos A ,得c =2b ·b 2+c 2-a 22bc .整理得 a =b .又因为(a +b +c )(a +b -c )=3ab ,所以a 2+b 2-c 2=ab ,即cos C =a 2+b 2-c 22ab =12.故C =π3.又a =b ,所以△ABC 为等边三角形.10.在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,且2b ·cos A =c ·cos A +a ·cos C(1)求角A 的大小;(2)若a =7,b +c =4,求bc 的值.解:(1)根据正弦定理2b ·cos A =c ·cos A +a ·cos C ⇒2cos A sin B =sin A cos C +cos A sin C =sin (A +C )=sin B ,∵sin B ≠0,∴cos A =12,∵0°<A <180°,∴A =60°.(2)由余弦定理得:7=a 2=b 2+c 2-2bc ·cos 60°=b 2+c 2-bc =(b +c )2-3bc ,把 b +c =4代入得bc =3,故bc =3.必修五第三讲 正、余弦定理在三角形中的应用知识梳理三角形的面积公式(1)S =12a ·h a (h a 表示a 边上的高).(2)S =12ab sin C =12bc sin A =12ac sin B .三角形的面积公式S =12ab sin C 与原来的面积公式S =12a ·h (h 为a 边上的高)的关系为:h =b sin C ,实质上b sin C 就是△ABC 中a 边上的高.题型分析[例1] 在△ABC 中,已知C =[解] 由正弦定理知AB sin C =AC sin B ,即23sin 120°=2sin B ,所以sin B =12,由于AB >AC ,所以C >B ,故B =30°.从而A =180°-120°-30°=30°.所以△ABC 的面积S =12AB ·AC ·sin A =12·23·2·sin 30°= 3.[变式训练].(1)在△ABC 中,若A =60°,b =16,S △ABC =643,则c =________.(2)在△ABC 中,若a =3,b =2,c =4,则其面积等于________.解析:(1)由已知得S △ABC =12·bc ·sin A ,即643=12×16×c ×sin 60°,解得c =16.(2)由余弦定理得cos A =b 2+c 2-a 22bc =4+16-92×2×4=1116,所以sin A =1-cos 2 A =31516,于是S △ABC =12bc sin A =12×2×4×31516=3154.答案:(1)16 (2)3154[例2] 在△ABC 中,求证:a -c cos B b -c cos A =sin Bsin A.[解] 法一:左边=a -c (a 2+c 2-b 2)2ac b -c (b 2+c 2-a 2)2bc =a 2-c 2+b 22a ·2b b 2-c 2+a 2=b a =2R sin B 2R sin A =sin Bsin A=右边,其中R 为△ABC 外接圆的半径.∴a -c cos B b -c cos A =sin Bsin A.法二:左边=sin A -sin C cos B sin B -sin C cos A =sin (B +C )-sin C ·cos B sin (A +C )-sin C ·cos A =sin B cos C sin A cos C =sin Bsin A=右边,(cos C ≠0)∴a -c ·cos Bb -c ·cos A =sin B sin A.[变式训练].在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,求证:a b -ba =c ⎝⎛⎭⎫cos B b-cos A a .证明:由余弦定理的推论得cos B =a 2+c 2-b 22ac ,cos A =b 2+c 2-a 22bc,代入等式右边,得右边=c ⎝⎛⎭⎫a 2+c 2-b 22abc-b 2+c 2-a 22abc =2a 2-2b 22ab =a 2-b 2ab =a b -b a =左边,∴a b -ba =c ⎝⎛⎭⎫cos Bb -cos A a .[例3] (2012·江西高考)在△B -C )-1=6cos B cos C .(1)求cos A ; (2)若a =3,△ABC 的面积为22,求b ,c .[解] (1)由3cos(B -C )-1=6cos B cos C ,得3(cos B cos C -sin B sin C )=-1,即cos(B +C )=-13,从而cos A =-cos(B +C )=13.(2)由于0<A <π,cos A =13,所以sin A =223.又S △ABC =22,即12bc sin A =22,解得bc =6.由余弦定理a 2=b 2+c 2-2bc cos A ,得b 2+c 2=13,解方程组⎩⎪⎨⎪⎧ bc =6,b 2+c 2=13,得⎩⎪⎨⎪⎧ b =2,c =3,或⎩⎪⎨⎪⎧b =3,c =2.解决三角形的综合问题,除灵活运用正、余弦定理及三角形的有关知识外,一般还要用到三角函数、三角恒等变换、方程等知识.因此,掌握正、余弦定理,三角函数的公式和性质是解题关键.[变式训练].在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且满足cos A 2=255,AB ·AC =3.(1)求△ABC 的面积; (2)若b +c =6,求a 的值.解:(1)∵cos A 2=255,∴cos A =2cos 2A 2-1=35,sin A =45.又由AB ·AC =3,得bc cos A =3,∴bc =5,∴S △ABC =12bc sin A =2.(2)∵bc =5,b +c =6,∴b =5,c =1或b =1,c =5.由余弦定理,得a 2=b 2+c 2-2bc cos A =20, ∴a =2 5.[例4]如图,在四边形ABCD 中,AC =CD =12AB =1,AB ·AC =1,sin ∠BCD =35.(1)求BC 边的长;(2)求四边形ABCD 的面积.[解] (1)∵AC =CD =12AB =1,∴AB ·AC =AB ·AC ·cos ∠BAC =2cos ∠BAC =1,∴cos ∠BAC =12,∴∠BAC =60°.(3分)在△ABC 中,由余弦定理有:BC 2=AB 2+AC 2-2AB ·AC ·cos ∠BAC =22+12-2×2×1×12=3,∴BC =3(6分)(2)由(1)知,在△ABC 中有:AB 2=BC 2+AC 2,∴△ABC 为直角三角形,且∠ACB =90°,(7分) ∴S △ABC =12BC ·AC =12×3×1=32.(8分)又∠BCD =∠ACB +∠ACD =90°+∠ACD ,sin ∠BCD =35,∴cos ∠ACD =35,(9分)从而sin ∠ACD =1-cos 2∠ACD =45,(10分)∴S △ACD =12AC ·CD ·sin ∠ACD =12×1×1×45=25.(11分)∴S 四边形ABCD =S △ABC +S △ACD =32+25=4+5310.(12分)[变式训练]在△ABC ,中,AB =2,cos C =277,D 是AC 上一点,AD =2DC ,且cos ∠DBC =5714. 求:(1)∠BDA 的大小;(2) AD ·CB .解:(1)由已知得cos ∠DBC =5714,cos C =277,从而sin ∠DBC =2114,sin C =217,∴cos ∠BDA =cos(∠DBC +∠C )=5714×277-2114×217=12,∴∠BDA =π3.(2)设DC =x ,则AD =2x ,AC =3x ,设BC =a ,则在△DBC 中,由正弦定理得x sin ∠DBC =asin ∠BDC ,∴a =7x .在△ABC 中,由余弦定理,得4=(3x )2+(7x )2-2·3x ·7x ·277.解得x =1,∴AC =3,BC =7.∴AD ·CB =AD ·CB cos(π-C )=2×7×⎝⎛⎭⎫-277=-4. [随堂检测]1.已知△ABC 的面积为32,且b =2,c =3,则A 的大小为( )A .60°或120°B .60°C .120°D .30°或150°解析:选A 由S △ABC =12bc sin A 得32=12×2×3×sin A ,所以sin A =32,故A =60°或120°,故选A.2.在△ABC 中,若AC AB =cos Bcos C,则( )A .A =CB.A =B C .B =CD .以上都不正确解析:C ∵AC AB =sin B sin C =cos Bcos C ∴sin B cos C =cos B sin C ∴sin(B -C )=0又∵-π<B -C <π,∴B -C =0,即B =C .3.等腰△ABC 中,顶角A =120°,腰长AB =1,则底边BC 长为________. 解析:易知∠B =∠C =30°,由正弦定理知:BC sin 120°=1sin 30°,∴BC = 3.答案: 34.三角形的两边分别为3 cm,5 cm ,它们所夹角的余弦值为方程5x 2-7x -6=0的根,则这个三角形的面积为________.解析:方程5x 2-7x -6=0的两根为x 1=2,x 2=-35,因此两边夹角的余弦值等于-35,并可求得正弦值为45,于是三角形面积S =12×3×5×45=6(cm 2).答案:6 cm 25.在△ABC 中,若B =30°,AB =23,AC =2,求△ABC 的面积.解:∵AB =23,AC =2,B =30°,∴根据正弦定理,有sin C =AB sin B AC =23×122=32,又∵AB >AC ,∴C >B ,则C 有两解,(1)当C 为锐角时,C =60°,A =90°,∴S △ABC =12AB ·AC sin A =2 3.(2)当C 为钝角时,C =120°,A =30°,∴S △ABC =12AB ·AC sin A = 3.综上可知,△ABC 的面积为23或 3.课后作业一、选择题1.在△ABC 中,已知AB =2,BC =5,△ABC 的面积为4,若∠ABC =θ,则cos θ是( )A.35B.-35 C .±35 D .±45解析:选C ∵S △ABC =12AB ·BC sin ∠ABC =12×2×5×sin θ=4.∴sin θ=45.又θ∈(0,π),∴cos θ=±1-sin 2 θ=±35.2.在△ABC 中,已知A =30°,a =8,b =83,则△ABC 的面积为( )A .32 3 B.16 C .323或16 D .323或16 3解析:选D 在△ABC 中,由正弦定理a sin A =b sin B ,得sin B =b sin A a =83×128=32,又b >a ,∴B =60°或120°.当B =60°时,C =180°-30°-60°=90°,∴S △ABC =12×8×83=323;当B =120°时,C =180°-30°-120°=30°,∴S △ABC =12ab sin C =12×8×83×12=16 3.3.在△ABC 中,A =60°,AB =2,且△ABC 的面积S △ABC =32,则边BC 的边长为( ) A. 3B.3C.7 D .7解析:选A ∵S △ABC =12AB ·AC sin A =32,∴AC =1由余弦定理可得BC 2=AB 2+AC 2-2AB ·AC cos A=4+1-2×2×1×cos 60°=3.即BC = 3.4.△ABC 的周长为20,面积为103,A =60°,则BC 的边长等于( )A .5B.6 C .7D .8解析:选C 如图由题意得⎩⎪⎨⎪⎧a +b +c =20 (1)12bc sin 60°=10 3 (2)a 2=b 2+c 2-2bc cos 60° (3)由(2)得bc =40.由(3)得a 2=b 2+c 2-bc =(b +c )2-3bc =(20-a )2-3×40∴a =7.5.某人从出发点A 向正东走x m 后到B ,向左转150°再向前走3 m 到C ,测得△ABC 的面积为334 m 2,则此人这时离开出发点的距离为( )A .3 m B. 2 m C .2 3 m D. 3 m解析:选D 在△ABC 中,S =12AB ×BC sin B ,∴334=12×x ×3×sin 30°,∴x = 3.由余弦定理,得AC = AB 2+BC 2-2AB ×BC ×cos B =3+9-9= 3 (m).二、填空题6.△ABC 的两边长分别为2,3,其夹角的余弦值为13,则其外接圆的半径为________.解析:不妨设b =2,c =2,cos A =13,则a 2=b 2+c 2-2bc ·cos A =9,∴a =3.又∵sin A =1-cos 2 A =223,∴外接圆半径为R =a 2sin A =32·223=928.答案:9287.一艘船以4 km /h 的速度沿着与水流方向成120°的方向航行,已知河水流速为2 km/h ,则经过 3 h ,该船实际航程为________.解析:如图所示,在△ACD 中,AC =23,CD =43,∠ACD =60°,∴AD 2=12+48-2×23×43×12=36,∴AD =6,即该船实际航程为6 km.答案:6 km8.在△ABC 中,a =b +2,b =c +2,又知最大角的正弦等于32,则三边长为________.解析:由题意知a 边最大.sin A =32,∴A =120°,∴a 2=b 2+c 2-2bc cos A .∴a 2=(a -2)2+(a -4)2+(a -2)(a -4).∴a 2-9a +14=0,a =2(舍去),a =7.∴b =a -2=5,c =b -2=3.答案:a =7,b =5,c =3 三、解答题9.在△ABC 中,若c =4,b =7,BC 边上的中线AD 的长为72,求边长a .解:∵AD 是BC 边上的中线,∴可设CD =DB =x ,则CB =a =2x .∵c =4,b =7,AD =72,在△ACD 中,有cos C =72+x 2-(72)22×7×x ,在△ABC 中,有cos C =72+(2x )2-422×7×2x .∴49+x 2-49414x =49+4x 2-1628x 解得x=92.∴a =2x =9. 10.(2010·浙江高考)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,设S 为△ABC 的面积,满足S =34(a 2+b 2-c 2).(1)求角C 的大小;(2)求sin A +sin B 的最大值.解:(1)由题意可知12ab sin C =34·2ab cos C ,所以tan C =3,因为0<C <π,所以C =π3.(2)由已知sin A +sin B =sin A +sin(π-C -A )=sin A +sin(2π3-A )=sin A +32cos A +12sin A =3sin(A +π6)≤ 3.当△ABC 为正三角形时取等号,所以sin A +sin B 的最大值是 3.。
正余弦定理知识点及题型归纳

正余弦定理是三角学中的重要知识点,用于解决与三角形相关的问题。
下面是对正余弦定理的知识点及题型归纳:一、正弦定理1. 定义:在任意三角形ABC中,设角A、B、C所对应的边分别为a、b、c,那么有sinA/a = sinB/b = sinC/c。
2. 性质:-等式两边同时乘以任意非零常数,等式仍然成立;-等式两边同时除以相同的角,等式仍然成立;-等式两边同时取反函数,等式仍然成立。
3. 应用:-已知三个角的度数,求边长;-已知两个边的长度,求第三个边的长度;-已知一个角和一条边的长度,求另外两个角的度数;-已知一个角和两条边的长度,求第三个角的度数。
二、余弦定理1. 定义:在任意三角形ABC中,设角A、B、C所对应的边分别为a、b、c,那么有cosA = (b ²+ c²- a²) / (2bc)。
2. 性质:-等式两边同时乘以任意非零常数,等式仍然成立;-等式两边同时除以相同的角,等式仍然成立;-等式两边同时取反函数,等式仍然成立。
3. 应用:-已知三个角的度数,求边长;-已知两个边的长度,求第三个边的长度;-已知一个角和一条边的长度,求另外两个角的度数;-已知一个角和两条边的长度,求第三个角的度数。
三、题型归纳1. 已知三个角的度数,求边长:-根据正弦定理或余弦定理,将已知的角度代入公式中,求解边长;-如果已知的是弧度制的角度,需要将其转换为角度制。
2. 已知两个边的长度,求第三个边的长度:-根据正弦定理或余弦定理,将已知的两个边的长度代入公式中,求解第三个边的长度;-如果已知的是弧度制的角度,需要将其转换为角度制。
3. 已知一个角和一条边的长度,求另外两个角的度数:-根据正弦定理或余弦定理,将已知的角度和边的长度代入公式中,求解另外两个角的度数;-如果已知的是弧度制的角度,需要将其转换为角度制。
4. 已知一个角和两条边的长度,求第三个角的度数:-根据正弦定理或余弦定理,将已知的角度和两条边的长度代入公式中,求解第三个角的度数;-如果已知的是弧度制的角度,需要将其转换为角度制。
高中数学必修五公式整理

高中数学必修五公式声明:本文非原创,由于界面阅读感不好而本人进行重新排版。
第一章 三角函数一.正弦定理:2(sin sin sin a b cR R A B C===为三角形外接圆半径) 变形:2sin (sin )22sin (sin )22sin (sin )2a a R A A R b b R B B R c c R C C R ⎧==⎪⎪⎪==⎨⎪⎪==⎪⎩推论:::sin :sin :sin a b c A B C =二.余弦定理:三.三角形面积公式:111sin sin sin ,222ABC S bc A ac B ab C ∆===第二章 数列一.等差数列: 1.定义:a n+1-a n =d (常数)2.通项公式:()d n a a n ∙-+=11或()d m n a a m n ∙-+=3.求和公式:()()d n n n n a a a S n n 21211-+=+=4.重要性质(1)a a a a q p n m q p n m +=+⇒+=+(2) m,2m,32m m m S S S S S --仍成等差数列二.等比数列:1.定义:)0(1≠=+q q a a nn 2.通项公式:q a a n n 11-∙=或q a a mn m n -∙=3.求和公式: )(1q ,1==na S n )(1q 11)1(11≠--=--=qqa a q q a S n n n2222222222cos 2cos 2cos a b c bc Ab ac ac B c a b ab C =+-=+-=+-222222222cos 2cos 2cos 2b c a A bca cb B aca b c C ab+-=+-=+-=4.重要性质(1)a a a a q p n m q p n m =⇒+=+(2)()m,2m,32q 1m m m m S S S S S --≠-仍成等比数列或为奇数三.数列求和方法总结:1.等差等比数列求和可采用求和公式(公式法).2.非等差等比数列可考虑(分组求和法) ,(错位相减法)等转化为等差或等比数列再求和, 若不能转化为等差或等比数列则采用(拆项相消法)求和.注意(1):若数列的通项可分成两项之和(或三项之和)则可用(分组求和法)。
(完整版)必修五;正弦定理与余弦定理

必修五:正弦定理和余弦定理一:正弦定理1:定理内容:在一个三角形中,各边的长和它所对角的正弦的比相等,即R Cc B b A a 2sin sin sin ===(R 是三角形外接圆半径) 2:公式变形(1)R Aa C B A cb a 2sin sin sin sin ==++++ (2)⎪⎩⎪⎨⎧C R c B R b A R a sin 2sin 2sin 2===或R c C R b B R a A 2sin ,2sin ,2sin === (3)⎪⎩⎪⎨⎧B c C b A c C a A b B a sin sin sin sin sin sin ===(4)Rabc A bc B ac C ab S ABC 4sin 21sin 21sin 21====∆ 以下是ABC ∆内的边角关系:熟记(5)B A B A b a >⇔>⇔>sin sin (大边对大角)(6)B A B A cos cos <⇔>(7)⎪⎩⎪⎨⎧+=+=+=)sin(sin )sin(sin )sin(sin B A C C A B C B A 思考A cos 与)cos(C B +的关系(8)2cos 2sin C B A += (9)若AD 是ABC ∆的角平分线,则AC DC AB DB = 思考题:1:若B A sin sin =,则B A ,有什么关系?2:若B A 2sin 2sin =,则B A ,有什么关系?3:若B A cos cos =,则B A ,有什么关系?4:若21sin >A ,则角A 的范围是什么?解三角形:已知三角形的几个元素,求其他元素的过程叫做解三角形.例1:已知ABC ∆,根据下列条件,解三角形.(1)10,45,60=︒=∠︒=∠a B A .(2)︒=∠==120,4,3A b a .(3)︒=∠==30,4,6A b a .(4)︒=∠==30,16,8A b a .(5)︒=∠==30,4,3A b a .思考:在已知“边边角”的情况下,如何判断三角形多解的情况判断方法:(1)用正弦定理:比较正弦值与1的关系(2)作图法:用已知角所对的高与已知角所对的边长比较.练习:(1)若︒=∠==45,12,6A b a ,则符合条件的ABC ∆有几个?(2)若︒=∠==30,12,6A b a ,则符合条件的ABC ∆有几个?(3)若︒=∠==45,12,9A b a ,则符合条件的ABC ∆有几个?例2:根据下列条件,判断三角形形状.(1)C B A 222sin sin sin =+.(2)C B A cos sin 2sin =(3)B b A a cos cos =(4)A b B a tan tan 22=二:余弦定理1:定理内容:三角形任何一边的平方等于其他两边的平方和减去这两边与它们夹角的余弦的积的两倍.即A bc c b a cos 2222-+=B ac c a b cos 2222-+=C ab b a c cos 2222-+= 另一种形式:bca cb A 2cos 222-+=. 请写出另两个:例1:根据下列条件,解三角形.(1)在ABC ∆中,︒=∠==120,4,5C b a ,求边c .(2)在ABC ∆中,︒=∠==60,8,5C b a ,求边c .(3)在ABC ∆中,8,7,5===c b a ,求最大角与最小角的和.(4)在ABC ∆中,13:8:7sin :sin :sin =C B A ,求C cos .(5)在ABC ∆中,8,120,34=+︒=∠=b a C c ,求ABC ∆的面积.(6)在ABC ∆中,34,60,4=︒=∠=∆ABC S C c ,求ABC ∆的周长.(7)在ABC ∆中,1)(22=--bcc b a ,求A ∠. (8)在ABC ∆中,4,3,2===c b a ,判断ABC ∆的形状.(9)求证:在ABC ∆中,)cos cos cos (2222C ab B ac A bc c b a ++=++.(10)求证:平行四边形两对角线的平方和等于它各边的平方和.。
高中数学必修五1.1正弦定理和余弦定理 课件 (共34张PPT)

两种途径 根据所给条件确定三角形的形状,主要有两种途径: (1)化边为角;(2)化角为边,并常用正弦(余弦)定理实施边、角 转换.
双基自测 1.(人教A版教材习题改编)在△ABC中,A=60° ,B=75° ,a =10,则c等于( A.5 2 10 6 C. 3 ). B.10 2 D.5 6
a 解析 由A+B+C=180° ,知C=45° ,由正弦定理得: sin A = c 10 c 10 6 sin C,即 3= 2.∴c= 3 . 2 2 答案 C
sin A cos B 2.在△ABC 中,若 a = b ,则 B 的值为( A.30° 解析 B.45° C.60° D.90°
4. 已知两边和其中一边的对角, 解三角形时, 注意解的情况. 如 已知 a,b,A,则 A 为锐角 图形 A 为钝角或直角
关系 式 解的 个数
a<b sin A a=bsin A
bsin A<a< b 两解
a≥b a>b a≤b
无解
一解
一解 一解 无解
一条规律 在三角形中,大角对大边,大边对大角;大角的正弦值也较大, 正弦值较大的角也较大,即在△ABC 中,A>B⇔a>b⇔sin A >sin B. 两类问题 在解三角形时,正弦定理可解决两类问题:(1)已知两角及任一 边,求其它边或角; (2) 已知两边及一边的对角,求其它边或 角.情况(2)中结果可能有一解、两解、无解,应注意区分.余 弦定理可解决两类问题:(1)已知两边及夹角求第三边和其他两 角;(2)已知三边,求各角.
正弦定理和余弦定理
基础梳理 a b c 1.正弦定理:sin A=sin B=sin C=2R,其中 R 是三角形外接 圆的半径.由正弦定理可以变形为: (1)a∶b∶c=sin A∶sin B∶sin C; (2)a= 2Rsin A ,b= 2Rsin B ,c= 2Rsin C ; a b c (3)sin A=2R,sin B=2R,sin C=2R等形式,以解决不同的三 角形问题.
必修5知识点梳理
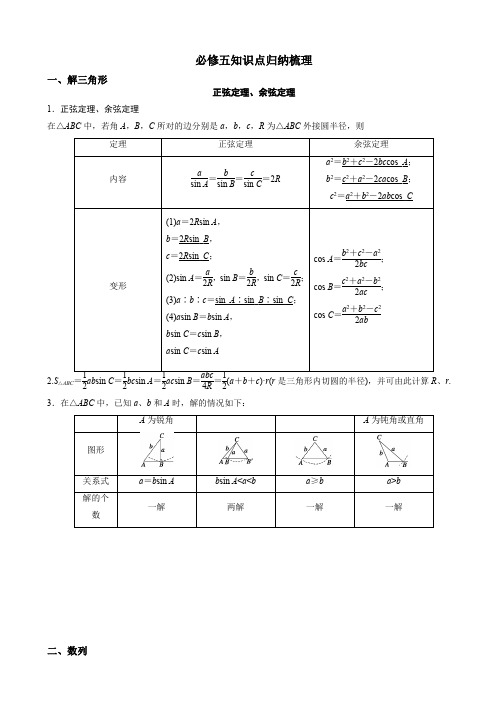
必修五知识点归纳梳理一、解三角形正弦定理、余弦定理1.正弦定理、余弦定理在△ABC中,若角A,B,C所对的边分别是a,b,c,R为△ABC外接圆半径,则2.S△ABC=12ab sin C=12bc sin A=12ac sin B=abc4R=12(a+b+c)·r(r是三角形内切圆的半径),并可由此计算R、r.3.在△ABC中,已知a、b和A时,解的情况如下:a=b sin A b sin A<a<b a≥b a>b 二、数列1.数列的定义按照一定顺序排列的一列数称为数列,数列中的每一个数叫做这个数列的项. 2.数列的分类3.数列的表示法数列有三种表示法,它们分别是列表法、图象法和解析法. 4.数列的通项公式如果数列{a n }的第n 项与序号n 之间的关系可以用一个式子来表示,那么这个公式叫做这个数列的通项公式.5.数列通项求法一、观察法观察法是求数列通项公式的最基本的方法,其实质就是通过观察数列的特征,找出各项共同的构成规律,横向看各项之间的关系结构,纵向看各项与项数之间的关系,从而确定出数列的通项二、公式法求通项直接利用等差数列或等比数列的定义求通项的方法叫定义法,这种方法适应于已知数列类型的题目.d n a a n )(11-+= (已知数列{a n }为等差数列) 11-*=n n b b q(已知数列{b n }为等比数列)三、由数列的前n 项和求数列通项(应用与的关系求通项)有些数列给出{}的前n 项和与的关系式=,利用该式写出,两式做差,再利用导出与的递推式,从而求出。
利用公式求解时,要注意对n 分类讨论,但若能合写时一定要合并.四、由数列的递推关系求通项公式对于递推公式确定的数列的求解,通常可以通过递推公式的变换,转化为等差数列或等比数列问题,有时也用到一些特殊的转化方法与特殊数列. 类型1:递推公式为nS na n a n S n a n S ()n f a 11()n n S f a ++=11n n n a S S ++=-1n a +n a n a ⎩⎨⎧≥⋅⋅⋅⋅⋅⋅⋅-=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=-211n S S n S a n nn n )(1n f a a n n +=+解法:把原递推公式转化为,利用累加法(逐差相加法)求解。
必修五正弦定理和余弦定理讲义

1.1 正弦定理和余弦定理一、正弦定理:在一个三角形中,各边和它所对角.......的正弦的比相等,即:A a sin =B b sin =C csin 注意:(1)正弦定理中,各边与其对角的正弦严格对应;(2)正弦定理中的比值是一个定值,具有一定几何意义,即为三角形外接圆的直径:A a sin =B b sin =Ccsin =2R [ R 指的是三角形外接圆半径 ];(3)正弦定理主要实现三角形中的边角互化.................;(4)S =C ab sin 21=A bc sin 21=B ac sin 21;(5)常用的公式: ①A +B +C =π,sin(A .....+.B)..=.sinC ....,. cos(A .....+.B)..=-..cosC ....,.tan(A .....+.B)..=-..tanC ....,.sin 2B A +=cos 2C ,cos 2B A +=sin 2C;②a =2RsinA ,b =2RsinB ,c =2RsinC ;③A >B ⇔a >b 【大角对大边】;④a +b >c ,a -b <c ;⑤a :b :c =sinA :sinB :sinC ;⑥a sinB =bsinA ,bsinC =csinB ,a sinC =csinA 。
例1:下列有关正弦定理的叙述:(1)正弦定理只适用于锐角三角形;(2)正弦定理不适用于直角三角形;(3)在某一确定的三角形中,各边与它所对角的正弦的比是一定值;(4)在△ABC 中,sinA :sinB :sinC = a :b :c 。
其中正确的个数有( ) A :1个 B :2个 C :3个 D :4个 【解析】:B变式练习1:在△ABC 中,角A :角B :角C =2 :1 :1,则a :b :c 等于( )A :4 :1 :1B :2 :1 :1C :2 :1 :1D :3 :1 :1 【解析】:C变式练习2:在△ABC 中,角A :角B :角C =4 :1 :1,则a :b :c 等于( )A :4 :1 :1B :2 :1 :1C :2 :1 :1D :3 :1 :1 【解析】:D例2:在△ABC 中,a =2,b =1,∠A =450,∠B =___________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【正弦定理】()1正弦定理:2sin sin sin a b c R ABC===,(2)推论:正余弦定理的边角互换功能① 2sin a R A =,2sin b R B =,2sin c R C =②sin 2a A R =,sin 2b B R=,sin 2c C R=③sin sin sin a bc ABC===sin sin sin a b c A B C++++=2R④::sin :sin :sin a b c A B C = (3)在三角形中:考查目标一:已知三角形两角及其中一角的对边求解三角形。
典例1.已知:在ABC ∆中, 45=∠A , 30=∠C ,10=c ,解此三角形。
同步练习:1.在ABC ∆中,(1)已知︒=75A ,︒=45B ,23=c ,求a ,b ; (2)已知︒=30A ,︒=120B ,12=b ,求a ,c .考查目标二:已知三角形两边及其中一边的对角求解三角形。
典例2.已知下列三角形的两边及其一边的对角,判断三角形的情况,有解的作出解答。
(1)a=7,b=9,A=100(2)a=10,b=20,A=75(3)a=10,c=56,C=60(4)a=2030A 6b 3==,,同步练习:已知下列各三角形的两边和其中一边的对角,先判断三角形是否有解?如果有解,再做出解答.(1)︒===10587A b a ,, (2)︒===802010A b a ,, (3)若△ABC 满足下列条件:① a = 4,b = 10,∠A = 30︒; ② a = 6,b = 10,∠A = 30︒; ③ a = 6,b = 10,∠A = 150︒; ④ a = 12,b = 10,∠A = 150︒; ⑤ a + b + c = 4,∠A = 30︒,∠B = 45︒.则△ABC 恰有一个的是( )A. ①④B. ①②③C. ④⑤D. ①②⑤1.有分别满足下列条件的两个三角形:(1)B=30°,a=14, b=7; (2) 那么下面判断正确的是( )A.(1)只有一解,(2)只有一解B.(1)有两解,(2)有两解C.(1)有两解,(2)只有一解D.(1)只有一解,(2)有两解 11. 满足条件a=4,b=23,A=︒45的△ABC 的个数是 ( ) A. 1个 B. 2个 C. 无数个 D. 不存在2.若三角形的三个角的比是1:2:3,最大的边是20,则最小的边是_____.考察目标三:求三角形面积。
典例3:在ABC 2AC 32AB 30B ABC 0∆===∆,求,,中,若的面积。
同步练习:仿照正弦定理的证法一,证明C ab S ABC sin 21=∆,并运用此结论解决下面问题:(1)在ABC ∆中,已知2=a ,3=b ,︒=150C ,求ABC S ∆;(2)在ABC ∆中,已知10=c ,︒=45A ,︒=30C ,求b 和ABC S ∆;【余弦定理】()2余弦定理:222222222222222222cos ,22cos ,2cos ,cos ,22cos .cos .2b c aA bca b c bc A a c b b a c ac B B ac c a b ab C a b c C ab ⎧+-=⎪⎧⎪=+-+-⎪⎪=+-⇒=⎨⎨=+-⎪⎪⎩+-⎪=⎪⎩【熟悉公式】例1:在∆ABC 中,a=1,b=2,∠c=120°求c 的值。
例2:在∆ABC 中,已知a=22,b =23,c=26+,求三内角A 、B 、C 。
同步练习:1、平行四边形两角邻边的长分别为64和34,它们的夹角为 45,求这个平行四边形的两条对角线的长与它们面积。
2、在∆ABC 中,已知74,56,84===c b a ,求A 及ABC S ∆3、在△ABC 中,sinA:sinB:sinC=3:2:4, 则cosC 的值为( )A. - 1/4B.1/4C. - 2/3D.2/34、在△ABC 中,若sinA :sinB :sinC=5:7:8,则B 的大小是( ) A.3πB.6πC.32πD.3π或32π5、在△ABC 中,若sinA :sinB :sinC=3:2:4,则cosC 的值为 ( )A.32B. 32-C.41D. 41-6、已知△ABC 的三内角的正弦之比为4:5:6, 周长为7.5,则其三边长为____________. 【判断三角形形状】【解题思路】:判定三角形形状时,一般考虑两个方向进行变形:(1)一个方向是边,走代数变形之路,通常是正、余弦定理结合使用; (2)另一个方向是角,走三角变形之路.通常是运用正弦定理0、在△ABC 中,已知a=7,b=10,c=6,则△ABC 的形状是( )A. 钝角三角形B. 锐角三角形C. 直角三角形D. 等边三角形2、在⊿ABC 中,如果(a+b+c)(b+c-a)=3bc,且sinA=2sinBcosC,试确定⊿ABC 的形状。
3、已知⊿ABC 中,三个内角A,B,C 的对边分别是a,b,c,若⊿ABC 的面积为S,且2S=(a+b)²-c²,求tanC 的值。
4、【公式变形转化】1、在⊿ABC 中,已知a=2,则bcosC+ccosB 等于______.2、在⊿ABC 中,如果(a+b+c)(b+c-a)=3bc,那么A 等于( ) A.30° B.60° C.120° D.150°3、已知⊿ABC 中,∠A=60°,最大边和最小边的长是方程3x²-27x+32=0的两实根,那么BC 边长等于______. 【提高题】1、在△ABC 中,A=︒60,b=1,且面积为3,则=++++CB A c b a sin sin sin ( )A. 338 B. 3392 C. 3326 D. 322、在△ABC 中,A=3π,BC=3,则△ABC 的周长为( )A. 3)3s i n (34++πB B. 3)6sin(34++πBC. 3)3sin(6++πB D.3)6sin(6++πB3、在△ABC 中,三个内角A 、B 、C 满足:)cos (cos sin sin sin C B A C B +=+, 则角A 为( )A. 2πB. 3πC. 6πD. 34π4、 在△ABC 中,若CcB b A a cos cos cos ==,则△ABC 是( )C B A c b a c b a C B A ABC sin )sin(,,,,,222-=-∆证明:对边分别为中,角在A. 直角三角形B. 等边三角形C. 钝角三角形D. 等腰直角三角形5、若△ABC 的三内角A ,B ,C 成等差数列,则cos 2 A + cos 2C 的最小值为 .6、在△ABC 中,若∠C = 60º,则cos A cos B 的取值范围是( )A. ⎥⎦⎤⎢⎣⎡-41 21,B. ⎥⎦⎤⎢⎣⎡41 0, C. ⎥⎦⎤⎢⎣⎡-41 43,D. 以上都不对【计算题】6、如图,在四边形ABCD 中,已知AD ⊥CD, AD=10, AB=14, ∠BDA=60︒, ∠BCD=135︒ 求BC 的长为多少?24. 已知A 、B 、C 为△ABC 的三个内角,它们的对边分别为a 、b 、c ,若m =(cosB ,sinC ),n =(cosC ,-sinB ),且m ·n =21.(1)求A ;(2)若a=32,△ABC 的面积S=3,求b+c 的值.25. 在△ABC 中,cosB=135-,cosC=54.(1)求sinA 的值; (2)设△ABC 的面积为233,求BC 的长.26. 三角形ABC 中的三个内角A 、B 、C 的对边分别为a 、b 、c ,已知ac b c a +=+222,且a :c=(3+1):2,求角C 的大小.DCA27. 在△ABC 中, 角A 、B 、C 所对的边长分别为a 、b 、c ,设a 、b 、c 满足条件222a bc c b =-+和bc =21+3,求A 和tanB 的值.3. 在△ABC 中,a ,b ,c 分别为角 A ,B ,C 的对边,且272cos 2sin 42=-+A C B .(1)求∠A 的大小;(2)若a =3,b + c = 3,求b 和c 的值.(三)典例分析: 问题1.在ABC △中,,,a b c 分别是三个内角,,A B C 的对边.如果()()22sin abA B +⋅-=()()22sin ,abA B -⋅+且A B ≠.求证:A B C △为直角三角形问题2.()1求22sin20cos 8020cos 80︒+︒+︒︒()2在A B C △中,角A 、B 、C 对边分别为a 、b 、c ,求证:()222sin sin A B a b cC--=问题 3.在A B C △中,,,a b c 分别是三个内角,,A B C 的对边,且274sincos 222B C A +-=.()1求角A 的度数;()2若 3.a b c =+=求,b c 的值问题4.(05天津)在A B C △中,CB A ∠∠∠、、所对的边长分别为c b a 、、,设c b a 、、满足条件222a bc cb =-+和12cb=+,求A ∠和B tan 的值(四)课后作业:1.(08届孝昌二中高三质检A B C 中,已知222sin sin sin sin B C A A C --=,则B ∠的大小为.A 150︒ .B 30︒.C 120︒.D 60︒2.(07届高三西安中学3月月考)已知锐角A B C △中,角,,A B C 的对边分别为c b a ,,,且2223tan bc a ac B -+=;()1求B ∠;()2求函数()sin 2sin cos f x x B x =+0,2x π⎛⎫⎡⎤∈⎪⎢⎥⎣⎦⎝⎭的最大. 3.已知A B C △的面积()22S a b c =--,且8b c +=,求A B C △面积的最大值。
