控制图应用步骤
第六章控制图、过程能力和直方图
在工序控制中需要了解的三个方面，都能在控制图上得到。 (1) 在连续的生产监控中，有无变化的征兆； (2) 有无急剧的变化； (3) 有无越出控制范围的异常值。
－－控制图的作用：
在质量诊断方面，可以用来度量过程的稳定性，即过程是否处于统计控制状态； 在质量控制方面，可以用来确定什么时候需要对过程加以调整，而什么时候则需使过程保持相应的稳定状态； 在质量改进方面，可以用来确认某过程是否得到了改进。
1.864
1.816
1.777
E2
2.660
1.772
1.457
1.290
1.134
1.109
1.054
1.010
0.975
m3A2
1.880
1.187
0.796
0.691
0.549
0.509
0.430
0.410
0.360
D3
－
－
－
－
－
0.076
0.136
0.184
0.223
d2
1.128
1.693
P
－
n －
（1－ ）
Pn
－
Pn
－
3
u
－
3
n
u
－
＋
u
－
3
n
u -
c
－
3
c —
c
－
3
c ＋
控制系数选用表
n
2
3
4
5
6
7
8
9
10
A2
1.880
1.023
0.729
0.577
0.483
Xbar—R控制图的操作步骤及应用示例
X—R控制图的操作步骤及应用示例用于控制对象为长度、重量、强度、纯度、时间、收率和生产量等计量值的场合。
X控制图主要用于观察正态分布的均值的变化，R控制图主要用于观察正态分布分散或变异情况的变化，而X-R控制图则将二者联合运用，用于观察正态分布的变化。
X-R控制图的操作步骤步骤1：确定控制对象，或称统计量。
这里要注意下列各点：（1）选择技术上最重要的控制对象。
（2）若指标之间有因果关系，则宁可取作为因的指标为统计量。
（3）控制对象要明确，并为大家理解与同意。
（4）控制对象要能以数字来表示。
（5）控制对象要选择容易测定并对过程容易采取措施者。
步骤2：取预备数据（Preliminary data）。
（1）取25个子组。
（2）子组大小取为多少？国标推荐样本量为4或5。
（3）合理子组原则。
合理子组原则是由休哈特本人提出的，其内容是：“组内差异只由偶因造成，组间差异主要由异因造成”。
其中，前一句的目的是保证控制图上、下控制线的间隔距离6σ为最小，从而对异因能够及时发出统计信号。
由此我们在取样本组，即子组时应在短间隔内取，以避免异因进入。
根据后一句，为了便于发现异因，在过程不稳，变化激烈时应多抽取样本，而在过程平稳时，则可少抽取样本。
如不遵守上述合理子组原则，则在最坏情况下，可使控制图失去控制的作用。
步骤3：计算Xi，Ri。
步骤4：计算X，R。
步骤5：计算R图控制线并作图。
步骤6：将预备数据点绘在R图中，并对状态进行判断。
若稳，则进行步骤7；若不稳，则除去可查明原因后转入步骤2重新进行判断。
步骤7：计算X图控制线并作图。
将预备数据点绘在X图中，对状态进行判断。
若稳，则进行步骤8；若不稳，则除去可查明原因后转入步骤2重新进行判断。
步骤8：计算过程能力指数并检验其是否满足技术要求。
若过程能力指数满足技术要求，则转入步骤9。
步骤9：延长X-R控制图的控制线，作控制用控制图，进行日常管理。
上述步1~步骤8为分析用控制图。
实施控制图的五个步骤
实施控制图的五个步骤1. 收集数据在实施控制图之前，首先需要收集相关的数据。
这些数据可以是产品质量，生产过程中的参数，设备的运行时间等等。
数据的收集可以通过手工记录、自动采集或者传感器等方式进行。
在收集数据时，要确保数据的准确性和完整性，避免漏报和误报。
•选择目标指标：确定需要监控和控制的目标指标，如产品质量指标、生产效率指标等。
•确定数据采集方式：选择适合的数据采集方式，可通过扫描仪、传感器、自动采集软件等方式进行。
•确保数据的准确性：采集数据时要注意数据的准确性，避免人为误差或设备故障导致的数据错误。
2. 分析数据收集到数据之后，需要对数据进行分析，以了解当前情况和趋势。
数据分析可以通过统计方法、图表分析等方式进行。
•数据清洗和处理：对收集到的数据进行清洗和处理，去除异常值和重复数据，保证数据的准确性。
•统计分析：使用统计方法对数据进行分析，如计算平均值、标准差、极差等，以了解数据的分布情况和变动趋势。
•图表分析：通过绘制控制图、趋势图等图表，将数据可视化，以便更直观地了解数据的变化趋势。
3. 建立控制图建立控制图是实施控制图的核心步骤，它可以帮助我们监控和控制过程的稳定性和可靠性。
建立控制图时，需要确定控制限和参数的计算方式。
•确定控制限：根据数据的统计分析结果，确定控制图的控制限。
常用的控制限有平均线、上下控制限和警戒线等。
•计算参数：根据数据的分布情况和变动趋势，计算控制图所需的参数，如平均值、标准差、极差等。
•绘制控制图：根据建立的控制限和计算的参数，使用统计软件或Excel等工具绘制控制图。
4. 分析控制图分析控制图是判断过程是否稳定的关键步骤。
通过对控制图的分析，可以了解过程的稳定性和可靠性，并及时发现异常和特殊因素。
•判断稳定性：观察控制图上是否存在超出控制限的点，如果存在，则说明过程可能存在特殊因素。
•判断规律性：根据控制图上点的分布情况，判断是否存在规律性，如趋势、周期性等。
控制图的作法及使用(教材)
二:管制图原理
μ- kσ
μ
μ+kσ
二:管制图原理
当一分配经证实为一常态分配时,则算出此常
态分配之标准差σ及平均值μ后，其特性可用 下列图表说明：
μ±kσ μ±0.67σ 在内机率 50.00% 在外机率 50.00%
μ±1σ μ±1.96σ μ±2σ μ±2.58σ
μ±3σ
68.26% 95.00% 95.45% 99.00%
1.3 非机遇原因 又称为：可避免之原因、人为原因、
特殊原因、异常原因、 局部原因等等。 例如: Δ 未遵照操作标准而操作，所发生之变异。 Δ 虽然遵照操作标准，但操作标准不完善，以致 发 生之变异。 Δ 机器设备之变动，发生之变异。 Δ 操作人员之更动，造成之变异。 Δ 原材料之不同，发生之变异。 Δ 量具不准确，造成之变异 。
二 .管制图原理 二:管制图原理
2.何谓变异性
在生产中变异永远存在.例如:同种原料内的变
化,机械的振动,当这些变化量极小时,制程仍 可被接受.这些称为机遇原因(chance cause) 或一般原因(common cause),称其在管制中 (in control)。
二 .管制图原理 二:管制图原理
一:管制图的概论
1. 所谓管制图:管制图上均包含有中心线
(Central line (CL)) 及上下两条管制界线 [Uppe r and Lowe r Control Lim i ts, (UCL)(LCL)]，用以测知制程是否在正常状态 。 2. 管制图系于 1924 年由美国品管大师 W. A . S h e w h a r t 博士发明。
7．c控制图（缺陷数控制图） 用于控制一部机器，一个部件，一定长度，
控制图的实施步骤
控制图的实施步骤简介控制图是质量管理中常用的一种统计工具，用于监控和改进过程稳定性和一致性。
它能够帮助我们识别生产过程中的特殊原因变异，及时采取措施进行改进。
本文将介绍控制图的实施步骤，并给出相应的操作指南。
步骤一：收集数据收集数据是实施控制图的第一步，通过收集过程中产生的相关数据，我们可以对过程的稳定性和一致性进行分析。
数据可以是连续型的，也可以是离散型的，关键是确保数据的准确性和完整性。
在收集数据时，需要考虑以下几个要点： - 数据的选择：选择与所控制的过程相关的关键性能指标进行收集。
- 数据的来源：可以从生产线上直接获取数据，也可以通过抽样检查的方式获取。
- 数据的记录：将数据记录在一个可靠的数据库中，以便后续的分析和使用。
步骤二：绘制控制图在步骤一中收集到数据之后，我们需要将数据绘制成控制图，以便于直观地观察过程的稳定性和一致性。
常见的控制图包括： - 均值控制图：用于监控过程的平均水平是否稳定。
- 范围控制图：用于监控过程的变异程度是否稳定。
- 过程能力指标控制图：用于评估过程的能力和稳定性。
在绘制控制图时，需要按照以下步骤进行操作： 1. 确定控制图的类型：根据所要监控的指标类型，选择合适的控制图类型。
2. 计算控制限：根据所收集的数据计算控制限，常见的控制限包括上限、中线和下限。
3. 绘制控制图：使用数据和计算得出的控制限，将数据点绘制在控制图上。
可以使用Excel等软件进行绘制，也可以使用统计软件进行自动生成。
步骤三：分析控制图绘制好控制图之后，我们需要对控制图进行分析，以便判断过程的稳定性和一致性。
主要的分析方法包括： - 规则检验法：通过检查控制图中的点是否满足特定的规则，来判断过程是否处于控制状态。
- 趋势分析法：通过观察控制图中的趋势，来判断过程的变化趋势。
- 频率分析法：通过计算控制图中的异常点的频率，来判断过程是否存在特殊原因变异。
分析控制图时，需要注意以下几点： - 了解各种规则和趋势的意义。
运用控制图进行控制教学
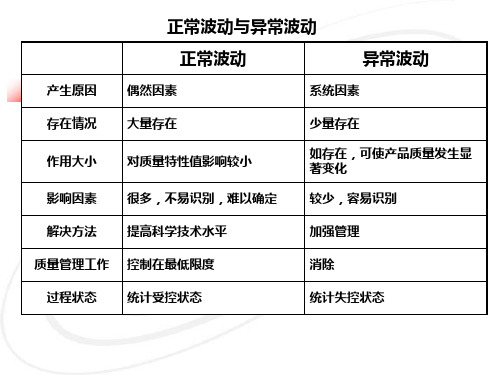
偶然性波动（正常波动）
工序质量控制的任务是使正常波动维持在适度的范围内
系统性波动（异常波动）
工序质量控制的任务是及时发现异常波动，查明原因，采 取有效的技术组织消除系统性波动，使生产过程重新回到 受控状态。
质量管理的一项重要工作，就是要找出产品质量波动 规律，把正常波动控制在合理范围内，消除系统原因 引起的异常波动。
D4 3.267 2.574 2.282 2.114 2.004 1.924 1.864
均值-极差控制图 -控制限
均值控制图
CL x UCL x A2R LCL x A2R
极差控制图
CL R UCL D4R LCL D3R
一个实例 （一）
一台自动螺丝车床已经准备好了加工切断长度的图 纸公差为0.500±0.008英寸的螺栓。
过程实际上没有失控而虚报失控，这类错误发生的概率 记为α。
2. 第二类错误：漏发警报
过程已经异常，但仍会有部分产品落在控制线内，这 类错误发生的概率记为β。
由于控制图是通过抽查来监控产品质量的,故两类错误是不可 避免的。
在控制图上,中心线一般是对称轴,所能变动的只是上下控制限 的间距。
若将间距增大,则α减小而β增大,反之,则α增大而β减小。因此, 只能根据这两类错误造成的总损失最小来确定上下控制界限。
规格是用来区分产品的合格与不合格
控制图的控制界限是用来区分偶然波动与 异常波动,即区分偶然因素与异常因素这两 类因素的。
利用规格界限显示产品质量合格或不合格 的图是显示图,现场可以应用显示图,但不 能作为控制图来使用。
一般情况下,控制界限严于规格;
小概率事件原理
P( 3 x 3 ) 0.9973
即过程的离散程度。
控制图的原理及应用
本：
，其平均值 x1, x有2,如…,下xn性质：
x
E(x)
(x)
n
和 则可通过k组大小为n的样本得到：
ˆ x
ˆ R
d2
其中， 是由n来d2确定的控制系数，可以通过查取计量控制图系数表（见表7-4）
得到。
12
二、计量值控制图
• 所以，由控制界限的一般公式即可得到图的控制界限为：
• 式中，
4
一、控制图基本原理
质 量 特 性 值
O
UCL CL
LCL 样本组号
5
一、控制图基本原理
（二）控制图的统计原理
1． 原理 3
当质量特性值服从正态分布时， 3即
X ~ N(, 2)
如果 生E(产X )过程中仅存在偶然因素，那么其产品质量特性值将会有
99.73%落在
的范围内。 3
6
一、控制图基本原理
c4
由此可以得到 图中x s 图的控x制界限为：
UCL
3 x 3s
n
c4 n
CL x
x
A3s
LCL
3
n
x
3s c4 n
x
A3s
• 式中
A3
3 c4
n
18
二、计量值控制图
• s图的控制界限为：
UCL c4 3
1 c42
3 s
1 c42 s c4
B4s
CL c4 s
LCL
• （三）控制图的分类——计量
分布 控制图类型 符号表示
适用范围及特点
平均值—极 差
控制图
xR 图
用于判断过程质量特性的均值以及极差（间接估算标 准差）是否处于所要求的水平，针对重量、长度、强 度等计量值控制对象，适用于产品批量较大且较为稳 定的工序，是最常用、最基本的控制图。判断工序异 常的灵敏度高，且极差计算工作量小
控制图应用(计数型)
控制图建立与结果分析
控制图类型选择
根据数据特点，选择p控制图（不良品率控制图） 进行分析。
数据点绘制
将每个样本的不良品率绘制在控制图上，形成数 据点。
控制限计算
根据历史数据或经验，计算出控制图的中心线 （CL）、上控制限（UCL）和下控制限（LCL）。
结果分析
通过观察数据点的分布情况，判断生产过程是否 处于受控状态。如果发现数据点超出控制限或呈 现非随机分布，则表明生产过程可能存在异常， 需要进一步调查原因并采取措施。
产品或过程。
04 计数型控制图应用步骤
CHAPTER
数据收集与整理
明确数据收集目的
确定要解决的问题或目标，例 如分析产品缺陷、评估过程稳
定性等。
选择合适的数据类型
根据目的选择计数型数据，如 不良品数、缺陷数等。
确定数据收集计划
包括收集时间、频率、样本量 等。
数据整理与预处理
对数据进行清洗、分类、汇总 等预处理操作，以便于后续分
案例总结与启示
案例总结
通过应用计数型控制图，该企业成功地发现了生产过程中的异常波动，并及时采取了相应的措施进行调整，最终 使产品质量得到了有效控制。
启示
计数型控制图是一种有效的质量控制工具，可以帮助企业及时发现生产过程中的问题并采取相应的措施进行改进。 在实际应用中，需要结合行业特点和数据特点选择合适的控制图类型，并严格按照控制图的建立和分析步骤进行 操作，以确保结果的准确性和可靠性。
原理
02
统计样本中不合格品的数量，然后与预设的控制限进行比较，
以判断生产过程是否处于受控状态。
应用场景
03
适用于生产批量小、检验费用低且要求不合格品数较少的产品
SPC控制图使用步骤
计量型控制图公式
中心线
CL X = X 控制限
UCLX=X+A2R UCLR=D4R
CLR=R
LCLX=X-A2R LCLR=D3R
不合格品率图（P图）
单个子组内不合格品率
PI=NPI / NI NI : 被检零件的数量 NPI ：发现的不合格零件数量 平均不合格品率：
CPL=
X-LSL 3 δC
X-LSL =
3（R/D2）
PPK
PP：性能指数 USL-LSL
PP=
6 δP
USL-LSL =
6S
PPK≤PP （双边公差） pPK等于PPU和PPL中的最小值。 δP ：过程总变差， 可以用 S估计 USL：公差上限 LSL：公差下限
PPK
标准差S计算 （XI-X）2
使用现有子组大小的计算
δc=R/D2 R：子组极差的平均值 n :一个子组内样本的数量 D2:随样本容量n变化的常数
控制图典型特殊原因准则汇总
1、一个点距中心线超过3根标准差 2、连续7点在中心线的同一侧 3、6点连续上升或下降 4、连续14点交替上升或下降 5、连续3点中有2点距中心线大于2个标准差（同侧） 6、连续5点中有4点距中心线大于一个标准差（同侧） 7、连续15个点在距中心线一个标准差内（两侧） 8、连续8个点距中心线大于1个标准差（两侧）
公差说明
单边规格：只有规格上限和规格中心或只有 下限或规格中心的规格;如考试成绩不得低于 80分，或浮高不得超过0.5mm等；此時數據 越接近上限或下限越好﹔
双边规格：有上下限與中心值,而上下限與中 心值對稱的规格；此时数据越接近中心值越 好；如D854前加工脚长规格2.8±0.2mm;
X-R控制图操作及应用
• 按上述原则判别定，可能会出现两个误判；
• （1）即冒失者之误：落入控制图的机率为99.97%，也就是 说1000个数据，有3个数据可能逸出控制界外，这是随机原 因，不是异常原因造成的变异。属正常，但误判为异常，此 现象为冒失者之误。用α表示。如α=0.3%。
• （2）迷糊者之误：测量值全部落在控制图中，且无倾向性， 通常也会认为属随机原因变异，而判定为正常。但是，实际 测量数据的分布中心已经偏离了设计规范中心，此时，肯定 存在变异，只是抽样时未碰到而已。这种误判，属迷糊者之 误，用β表示,一般来说, β发生的机率大于α机率。初次 使用SPC手法控制产品质量的QC人员经常会发生α和β两种 情况的误判。
和
作 • 3对于超出控制界限的点采取整改行动。
用 • 4根据样本数据可以对过程性质作出评价
• 5、评定生产/过程性质变化与原来过程状态进行比较。
• 节约成本 • 使标准趋于准确 • 使过程更加稳定 • 使控制规格更加真实 • 减少检验频度 • 减少问题出现的频度 • 改善和提高客户的满意度 • 可靠地测出实际过程能力 • 改善测量结果的准确度 • 改善产品品质 • 减少出货周期时间
• a . 输出值分布宽度减小，这常常是好的状态，应研 究以便推广应用和改进过程。
• b. 测量系统改变，这样会遮掩过程真实性能的变化。
UCLR
R
• C） 明显的非随机有规律变化图形：除了会出现超过 控制界的点或长链之外，数据中还可能出现其他的易 分辨的由于特殊原因造面的图形，属工序质量异常。
UCL
N2 3
4
5
67
8
9
10
d2 1.13 1.69 2.06 2.33 2.53 2.70 2.85 2.97 3.08
如何运用控制图进行控制
内容提要
控制图应用的两个阶段 运用控制图判断过程受控/失控 什么时候重新计算控制限 使用控制图应注意的问题
控制图应用的二个阶段
分析阶段 控制阶段
分析阶段
在控制图的设计阶段使用,主要用以确定 合理的控制界限
每一张控制图上的控制界限都是由该图上 的数据计算出来
每天只看目标，别老想障碍
•
3、
。22.3 .2223:5 9:2323: 59Mar-2222-M ar-22
宁愿辛苦一阵子，不要辛苦一辈子
•
4、
。23:5 9:2323: 59:232 3:59Tue sday, March 22, 2022
• •
积极向上的心态，是成功者的最基本要素 5、
。22.3 .2222.3 .2223:5 9:2323: 59:23M arch 22, 2022
控制图的应用程序
课 程 内 容 回 顾
每一个成功者都有一个开始。勇于开始，才能找到成
•
1、
功的路 。22.3.2222.3.22Tuesday, March 22, 2022
成功源于不懈的努力，人生最大的敌人是自己怯懦
•
2、
。2 3:59:23 23:59:2 323:593 /22/20 22 11:59:23 PM
生活总会给你谢另一个谢机会，大这个机家会叫明天 6、
。2 022年3 月22日 星期二 下午11 时59分 23秒23: 59:232 2.3.22
人生就像骑单车，想保持平衡就得往前走
•
7、
。202 2年3月 下午11 时59分 22.3.22 23:59M arch 22, 2022
•
8、业余生活要有意义，不要越轨。20 22年3 月22日 星期二1 1时59 分23秒2 3:59:23 22 March 2022
控制图的原理及应用教案
控制图的原理及应用教案一、控制图的概述•控制图是用来监测和分析过程稳定性的工具。
它能够帮助我们判断过程是否受到了特殊因素的影响，从而帮助我们定位问题和改进过程。
•控制图包括过程监控图、变动图、普通图等，每种图形都有其特定的使用场景和目的。
二、控制图的基本原理•均值控制图的原理：通过收集和分析过程数据，确定过程的中心线和控制上下限，根据数据的离散程度来判断过程的稳定性。
•范围控制图的原理：通过跟踪样本范围的变化，来评估过程的稳定性和一致性。
•动态测量控制图的原理：通过在过程控制中，采样循环中检测结果的变化，来判断过程的稳定性。
•经济控制图的原理：通过分析与经济因素相关的数据，来优化过程并减少资源的浪费。
三、控制图的应用场景1.生产过程监控：通过定期采样和测量关键参数，将数据绘制在控制图上，及时发现过程异常和问题并采取相应的纠正措施。
2.产品质量控制：通过控制图来监测产品参数的变化和偏离，确保产品质量在可接受范围内，并及时发现潜在问题。
3.供应链管理：通过掌握供应链中各个环节的数据，绘制控制图来分析供应链的稳定性和可靠性，及时处理延迟和异常情况。
4.服务质量监控：对于服务行业，可以使用控制图来衡量并监控关键指标，及时发现异常情况并采取相应的改进措施。
5.实验过程控制：在实验过程中，采用控制图能够帮助我们评估实验结果的稳定性和一致性，从而提高实验的可靠性。
四、控制图的应用步骤1.收集数据：需要收集与需要监控的过程相关的数据。
2.绘制控制图：选择适当的控制图类型并将数据绘制在控制图上。
3.判断过程稳定性：通过分析控制图数据的模式和规律，判断过程的稳定性。
4.分析过程问题：如果控制图中存在异常点或趋势，说明过程可能存在问题，需要进一步分析和排查。
5.纠正和改进：根据分析结果采取纠正措施，并对过程进行改进以提高稳定性和一致性。
6.持续监控：持续收集数据并绘制控制图，监控过程的稳定性和持续改进。
五、控制图的优势和局限性优势•提供直观的数据展示和分析方式，便于快速理解和判断过程稳定性。
控制图使用操作规程
4内容4。
1控制图的定义:控制图是对过程质量特性值进行测定、记录、评估，从而监察过程是否处于控制状态的一种用统计方法设计的图，图上有中心线CL、上控制限UCL、下控制限LCL。
4。
2常规控制图的原理4。
2.1控制图的形成，将通常的正态分布图转个方向，是自变量增加的方向垂直向上，将σμ3-μμσ、+分别标为CL、UCL、LCL，这样就得到了一张控制图。
3、4.2.2控制图的第一种解释：若过程正常，即分布不变，则出现这种点子超过UCL情况的概率只有1/1000左右；若过程异常，点子超过UCL情况的概率可能为1/1000的几十乃至几百倍。
用数学语言来说，这就是小概率事件原理：小概率事件在一次试验中几乎不可能发生，若发生即判断异常。
从图1可知点子在LCL与UCL之间的概率为99.73％.图14。
2。
3控制图的第二种解释：对质量产生的影响的因素按大小可分为：偶然因素、与异常因素。
偶因是过程固有的，始终存在,对质量的影响微小，但难以除去;异因则非过程固有,有时存在，有时不存在,对质量的影响大，但不难出去.若通过控制手段消除异因后，就只剩下偶因，这是正常波动，根据正常波动，应用统计学原理设计出控制图相应的控制界限，当异常波动发生时，点子机会落在界外，因此点子频频出界就表明存在异常波动。
控制图上的控制界限就是区分偶然波动与异常波动的科学界限。
4。
3常用术语n:子组大小，常用子组中观测值得个数。
k :子组数。
X :质量特性的观测值（可用,...,,321X X X 表示单个观测值）。
X ：子组平均值。
X ：子组平均值得平均值.μ：过程平均值的真值。
Me :子组中位数，对于一组升序或降序排列的n 个子组观测值，当n 为奇数时，Me 为该组中间的那个数，当n 为偶数时，Me 为该组中间2个数的平均值。
Me :中位数的平均值。
R :子组极差，子组观测值中最大值与最小值之差(在单值图下,代表移动极差，即2个相邻的观测值差值的绝对值)。
常规控制图的作法及其应用
广濑拓普康(东莞）电子有限公司常规控制图的作法及其应用一、各类常规控制图的使用场合1．X—R控制图用于控制对象为长度、重量、强度、纯度、时间、收率和生产量等计量值的场合。
X控制图主要用于观察正态分布的均值的变化，R控制图主要用于观察正态分布分散或变异情况的变化，而X—R控制图则将二者联合运用,用于观察正态分布的变化。
2．X-s控制图与X—R图相似，只是用标准差（s）图代替极差（R）图而已。
3．Me—R控制图与X-R图也很相似,只是用中位数（Me）图代替均值(X).4．X—Rs控制图多用于对每一个产品都进行检验，采用自动化检查和测量的场合。
5．p控制图用于控制对象为不合格品率或合格品率等计数质量指标的场合,使用p图时应选择重要的检查项目作为判断不合格品的依据；它用于控制不合格品率、交货延迟率、缺勤率、差错率等。
6．np控制图用于控制对象为不合格品数的场合。
设n为样本，p为不合格品率,则np为不合格品数.7．c控制图用于控制一部机器,一个部件，一定长度，一定面积或任何一定的单位中所出现的不合格数目。
焊接不良数/误记数/错误数/疵点/故障次数8．u控制图当上述一定的单位，也即n保持不变时可以应用c控制图，而当n有变化时则应换算为平均每项单位的不合格数后再使用u控制图.二、应用控制图需要考虑的一些问题1．控制图用于何处？对于所确定的控制对象—-统计量应能够定量，这样才能够应用计量控制图；如果只有定性的描述而不能够定量，那就只能应用计数控制图。
所控制的过程必须具有重复性，即具有统计规律。
2．如何选择控制对象?一个过程往往具有各种各样的特性，在使用控制图时应选择能够真正代表过程的主要指标作为控制对象。
3．怎样选择控制图？选择控制图主要考虑以下几点：首先根据所控制质量特性的数据性质来进行选择，如数据为连续值的应选择X—R图，X-s图,X-Rs图等；数据为计件值的应选择p或np图;数据为计点值的应选择c图或u图。
控制图应用步骤
1) 返抽回 样计划
1.抽样计划的原则：合理的子组，即：组内出现特殊原因的机会最小，组间 出现特殊原因的机会最大。（子组内的变差代表的是零件间的变差， 而子组间的变差代表的是过程的变化）。 即：观测值的个数或样本量决定了控制图反映波动的能力。
坐标表示控制统计量的值，横坐标表示时间的顺序； 5. 对观察记入日志的部分，这部分包括：过程调整、更
换工装、材料变更，或其它任何可能影响过程变化的 详细资料。（控制图格式见样表）※
样表
正面；
示例
背面※
3) 记录原始数量
1. 记录每一个单值及每一个子组的编号； 2. 记录任何有关的观察事项。※
4) 计算每一个子组的样本统计量
过程相对稳定系数评价
1. 过程稳定系数：
2. 相对稳定系数：
过程相对稳定系数 drσ ＜10%
10%≤ drσ ＜20% 20%≤ drσ ＜50%
drσ ≥50%
评价 接近稳定 不太稳定
不稳定 很不稳定
6西格玛相关
（一）连续型数据的流程能力
流程的西格玛水平：Z值 Z值可以描述流程的不合格率P(d)
控制图应用步骤
1. 收集数据
2. 建立控制限
3. 统计上受不 受控的解释
1)确定控制图中心线 2)确定控制图上控制限和下控制限
4. 为了持续控 制延长控制限
控制图的中心线和上/下控制线
计量型；
计数型※
控制图应用步骤
1. 收集数据
1)分析ห้องสมุดไป่ตู้差图上的点 (控制图判异)
控制图的原理及应用
4、样本中位数
把收集到的统计资料按大小顺序重新排列，排在正
中间的那个数就叫作中位数，用符号 ~x 表示；当n为奇
数时正中间的数只有一个，当n为偶数时，正中位置有两个 数，此时，中位数为正中间两个数的算术平均值。 如： 1）1.1， 1.3， 1.4 ， 1.2，1.5 2) 1.0， 1.2， 1.4，1.1
第二种错误(β) :消费者冒险率
生产质量非常差,已达到拒收水平,理应判为拒收,但由于控制线设置过 宽,导致产品异常还误判为合格.其机率称为消费者冒险率,因此种错误 使消费者蒙受损失故得名之. 此冒险率又称为第二种错误 (TYPE Ⅱ ERROR) 简称(β).
UБайду номын сангаасL
3
2
1
CL
1
2
3
LCL
控制图的原理及应用
本标准偏差，用符号S或σ表示，标准偏差又称标准差，其
计算公式为：
s
1
n
2
xi x
n1i1
沿用计算样本变异数的例子，则那五个统计资料的标准差：
s 1 242(34)2(44)2(54)2(64)2 51
1 2 2 ( 1) 2 0 2 1 2 2 2
4
10
2 .5 1 .58
世界上第一张控制图是休哈特在1924年5月16日提出的不合格品率p控制图。
控制图的原理及应用
三、控制图常用术语
1、统计资料及其分类 2、总体与样本的区别 3、不良数与缺点数 4、样本中位数 5、样本全距（极差） 6、样本变异数（方差） 7、样本标准偏差
控制图的原理及应用
1、统计资料的分类
统计资料
平均值波动，第一种特殊波动存在， 制程处于非统计控制状态
控制图作图步骤与实例
请大家分析判断:在X-R 图中,我们应先作哪一个 图?
X-R控制图的操作步骤
1.如果先作 X 图,则由于这时R图还未判稳, R 的数据不 可用,故不可行.
2.如果先作R图,则由于R图中只有 R 一个数据,可行.等R
图判稳后,再作 X 图. R图未判稳,则永不能开始作X 图.国际标准ISO8258:1991 也规定了在 X-R 图中必须先作 R 图.不但如此,注意, 所有正态分布的控制图都必须反其道而行之.
X-R控制图的操作步骤
步骤1：确定所控制的质量指标（控 制对象，或称统计量）。
这里要注意下列各点： 1）选择技术上是最重要的控制对象。 2）若指标之间有因果关系，则宁可取作为 因的指标为统计量。 3）控制对象可以是多个，这时需要应用多 指标控制图与多指标诊断。 4）控制对象要明确，并为大家理解和同意。
日 时 样本序号 Ni (Pn)i Pi 备注
P控制图的操作步骤
3.计算各样本的不合格品率及其均值,其计算公式: Pi=(Pn)i/ni
i=1,2,……k
式中:(pn) i为第i个样本的不合格数,也可记为di; ni为第i个 样本的大小;k为样本个数,一般不少于25. 4.计算中心线和控制界限
P图的中心线和控制界限计算公式:
X-R控制图的操作步骤
步骤3：计算Xi, Ri
步骤4：计算X，R。 步骤5：计算R图控制线、X 图控制线，并作图。 步骤6：将预备数据在R图中打点，判稳。若稳,则进行步骤 7;若不稳,则执行20字方针（查出异因，采取措施，保证 消除，不再出现，纳入标准）后转入步骤2重新开始.
X-R控制图的操作步骤
X-R控制图的操作步骤
5）控制对象要能以数字来表
示。
6）控制对象要选择容易测定 并对过程容易采取措施者。 7）直接选择对象有困难时可 采用代用特性进行测定。
X-R控制图操作及应用
感谢观看
THANKS
• 多变量控制图：未来X-R控制图可能向多变量方向发展，同时监测多个 质量特性，实现更全面的质量控制。
• 大数据应用：借助大数据技术，X-R控制图可以处理海量数据，挖掘更 多有价值的信息，为质量改进提供更准确的依据。
• 挑战与机遇并存：虽然X-R控制图在质量管理中具有重要作用，但随着 市场需求的不断变化和技术的快速发展，其面临着不断适应新需求、新 技术和新标准的挑战。同时，这也为X-R控制图的发展带来了更多的机 遇和创新空间。
观察点的分布情况
01
若点超出控制界限或呈现非随机分布，则可能存在异常因素。
分析点的变化趋势
02
若点呈现连续上升或下降趋势，则可能存在系统性问题。
比较不同时间段或不同产品的控制图
03
若存在显著差异，则可能存在异常因素。
案例分析：某产品质量异常因素识别
案例背景
某生产线上的产品质量出现波动，需识别 异常因素。
改进措施提出和实施效果评价
改进措施提出
针对生产过程的不稳定因素，提出相应的改进措施，如优化设备参数、加强员工培训、改进原材料质量等。
实施效果评价
在实施改进措施后，再次收集数据并绘制X-R控制图进行评估。通过比较改进前后的控制图表现，评价改进措施 的实施效果。在本案例中，实施改进措施后，生产过程的稳定性得到显著提升，样本点基本落在控制限内。
数据收集与整理要求
数据类型
收集计量值数据，如长度、重量、时间等连续型变量 。
数据量
通常至少需要25组以上的数据，以充分反映过程波动 。
数据整理
将数据按照时间顺序或随机顺序排列，并计算每组数 据的平均值和极差。
确定中心线和上下控制限
实施控制图的五个步骤图片
实施控制图的五个步骤第一步：确定需要监控的过程在实施控制图之前，首先需要确定需要监控的过程。
这个过程可以是任何一个可以被量化的业务或生产活动。
例如，可以监控产品的质量控制过程，监控生产线的效率等。
确定需要监控的过程是实施控制图的第一个关键步骤。
第二步：收集数据并建立样本在实施控制图之前，需要收集相关数据并建立样本。
收集数据可以通过检测、测量或观察等方式进行。
样本的建立是为了更好地反映整个过程的变化。
样本应该具有随机性和代表性。
第三步：确定控制图类型在实施控制图之前，需要根据数据的类型和监控的目的确定控制图的类型。
常见的控制图有平均数图、范围图、标准偏差图等。
不同类型的控制图可以反映不同类型的变化。
第四步：计算控制限在实施控制图之前，需要计算控制限。
控制限是用来判断过程是否处于控制状态的基准。
控制限的计算需要使用样本数据，并根据统计方法进行计算。
控制限通常包括上限和下限，超出这些限制的数据点可能表示有异常事件发生。
第五步：绘制控制图并分析结果在实施控制图之前，需要根据计算得到的控制限绘制控制图，并分析结果。
控制图通常包括样本点和控制限线。
通过对控制图的分析，可以判断过程是否处于控制状态，是否存在异常事件等。
如果过程处于控制状态，说明过程运行正常；如果过程超出控制限，说明需要进一步调整和改进过程。
以上是实施控制图的五个步骤。
通过这五个步骤，可以对需要监控的过程进行有效的控制和管理。
控制图可以帮助我们及时发现过程中的异常事件，并采取相应的措施进行调整和改进，从而提高过程的稳定性和可靠性。
在实施控制图之前，需要仔细思考每个步骤的具体内容，并根据实际情况进行灵活的调整和应用。
只有科学合理地实施控制图，才能有效地提高生产效率和质量水平。
快来尝试实施控制图吧，提升您的生产管理水平！。
实施控制图的五个步骤包括
实施控制图的五个步骤包括1. 定义过程和目标在使用控制图进行过程监控和改进之前，首先需要明确定义要控制的过程和目标。
过程是指一系列相关的活动或操作，目标是待改进的指标或性能。
明确定义过程的边界和目标可以帮助我们确定控制图的适用范围和目标。
2. 数据采集和整理为了绘制控制图，我们需要收集相关的数据。
数据可以来自过程的运行记录、传感器采集等。
收集到的数据需要进行整理，包括数据清洗、汇总和归类等操作。
整理后的数据应该具有一定的结构，便于后续的分析和绘图。
•清洗数据：去除异常值、缺失值等，保证数据的准确性和可靠性。
•汇总数据：按照一定的时间段或其他指标进行数据聚合，以便分析。
•归类数据：将数据按照不同的维度进行分类，便于后续的控制图绘制和解读。
3. 绘制控制图当数据收集和整理完成之后，下一步是绘制控制图。
控制图是一种统计工具，可以帮助我们分析过程在不同时间点的变化情况，并判断是否存在特殊原因导致的异常。
控制图通常由一条中心线和上下限线组成。
•中心线：代表过程的平均水平，可以通过计算数据的平均值来确定。
•上下限线：根据数据的变异性来确定，常用的方法包括极差法、标准差法等。
绘制控制图的过程包括计算中心线和上下限线的值，以及在图表上标出数据点。
常见的控制图包括均值控制图、极差控制图等。
4. 分析和解读控制图一旦控制图绘制完成，我们需要对图表进行分析和解读。
控制图可以帮助我们确定过程是否稳定，是否存在特殊原因引起的异常。
对控制图的分析通常包括以下几个步骤：•观察过程的变化趋势：通过观察数据点的分布情况，判断过程是否稳定。
•判断是否存在特殊原因：通过控制图上的规律性和异常点，判断是否存在特殊原因。
•进一步分析异常原因：如果发现异常，需要进一步分析异常的原因，并采取相应的措施进行改进。
5. 持续改进控制图的作用不仅仅是分析过程的稳定性和异常情况，更重要的是帮助我们持续改进。
通过对控制图的分析，我们可以识别出存在问题的环节和改进的方向，进而采取相应的措施进行改进。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
控制图的选择
控制图应用步骤
1. 收集数据
2. 建立控制限
3. 统计上受不 受控的解释
4. 为了持续控 制延长控制限
1)建立一个抽样计划 2)控制图的设置 3)记录原因数据 4)计算每一个子组样本的控制统计量 5)将控制统计量画在控制图上
1)确定控制图中心线 2)确定控制图上控制限和下控制限
1)分析极差图上的点 (控制图判异) 2)识别并标识特殊原因（R图） 3)重新计算控制限（R图） 4)识别和处理特殊原因（均值图） 5)重新计算控制限（均值图）
1. 按照控制图的类型，计算合适的统计量，可能是：样本均值， 中位数，极差，标准差，等。※
5) 将控制统计量画在控制图上
1. 将计算出来的控制统计量画在图上，确保所描的控制统计量的 点是一一对应的。将相邻两点用直线连接起来从而帮助显示模 式和趋势；
2. 注意：在描图过程中，如果发现有的点比别的点高很多或低很 多，应再次确认是否计算错误或描图错误，并查询相关的观察 记录。※
抽样间隔
不稳定
稳定
8小时
8小时
4小时
8小时
2小时
8小时
1小时
4小时
1小时
2小时
※
2) 控制图设置
1. 包括过程和抽样方法描述的表头信息； 2. 记录/显示所收集数据的实际值的部分，这应该包含日
期和时间或其它的子组编号； 3. 用于中间的数据计算的部分； 4. 对用于分析的每一个控制统计量描点的部分；通常纵
坐标表示控制统计量的值，横坐标表示时间的顺序； 5. 对观察记入日志的部分，这部分包括：过程调整、更
换工装、材料变更，或其它任何可能影响过程变化的 详细资料。（控制图格式见样表）※
样表
正面；
示例
背面※
3) 记录原始数量
1. 记录每一个单值及每一个子组的编号； 2. 记录任何有关的观察事项。※
4) 计算每一个子组的样本统计量
控制图分类---按数据类型
1. 计量型控制图
1) 单值与移动极差控制图（I-MR）。【 样本量n=1】 2) 均值极差控制图（XBar-R图）； 【样本量2 ≤n ≤9】
~ 3) 均值与标准差控制图（XBar-S图）；【样本量n ≥10】
4) 中位数与极差控制图（X-R图）；
2. 计数值控制图
1) 不良率控制图（P图）； 2) 不良数控制图（NP图）； 3) 缺点数控制图（C图）； 4) 单位缺点数控制图（U图）。※
控制图应用步骤
1. 收集数据
2. 建立控制限
3. 统计上受不 受控的解释
1)确定控制图中心线 2)确定控制图上控制限和下控制限
4. 为了持续控 制延长控制限
控制图的中心线和上/下控制线
计量型；
计数型※
控制图应用步骤
1. 收集数据
1)分析极差图上的点 (控制图判异)
2. 建立控制限
3. 统计上受不 受控的解释
过程能力和过程性能
计量型数据 过程能力和过程性能
1. 过程能力：仅适用于稳定统计过程，是过程固有变差的 6 范围，
式中
R
通常用 d 2
和S Leabharlann 2来估计。2.过程性能：过程总变差的
6
范围，式中
通过用标准差S来估计。
3.如果过程处于统计受控状态，过程能力非常接近于过程性能。当过
程的能力和性能
当过程受控时并经过过程能力评价满足要求时， 应可以延长控制限，以满足未来过程控制的需 要。如果过程中心线偏离目标值，可能需要针 对目标值进行调整。
1) 返抽回 样计划
1.抽样计划的原则：合理的子组，即：组内出现特殊原因的机会最小，组间 出现特殊原因的机会最大。（子组内的变差代表的是零件间的变差， 而子组间的变差代表的是过程的变化）。 即：观测值的个数或样本量决定了控制图反映波动的能力。
2.子组数量：为了建立控制限，通常取25个子组，或更多个子组包含100或 更多个单值读数。
3.子组容量：较大的子组能很容易探测出较小的过程变化。一般2-5个样本。 4.子组频率：通常按时间顺序来取子组，目的是探测过程随时间发生的变化。
推荐的频率见附表所示
附表 推荐的子组频率
每小时产量
10以下 10-19 20-49 50-99 100以上
4. 为了持续控 制延长控制限
2)识别并标识特殊原因（R图） 3)重新计算控制限（R图） 4)识别和处理特殊原因（均值图） 5)重新计算控制限（均值图）
控制图应用步骤
1. 收集数据
2. 建立控制限
3. 统计上受不 受控的解释
4. 为了持续控 制延长控制限
当过程受控时并经过过程能力评价满足要求时， 应可以延长控制限，以满足未来过程控制的需 要。如果过程中心线偏离目标值，可能需要针 对目标值进行调整。
ZUSL =
USL-X
ZLSL =
X-LSL
Z值与不合格率P(d)对应表
（二）可区分型数据流程能力
可区分型数据：通过/不通过 一次通过率First Time Yield FTY=合格数量/总数量
p(d)=1-FTY = 不合格数量/总数量
（二）可数型数据流程能力
数据不只是通过/不通过，还知道一件产品上与多少个缺点 DPU-Defects Per Unit 每件的平均缺点数 dpu=缺点总数量/总件数 FTY=e-dpu p(d)=1-FTY
控制图
上控制界限(UCL) 中心线(CL) 下控制界限(LCL)
控制图分类---按用途
1.分析用控制图： 根据样本数据计算出控制图的中心线和上、下控制界限，画出控制图，以便分析和判断过程是否 处于于稳定状态。如果分析结果显示过程有异常波动时，首先找出原因，采取措施，然后重新抽 取样本、测定数据、重新计算控制图界限进行分析。 2.控制用控制图： 经过上述分析证实过程稳定并能满足质量要求，此时的控制图可以用于现场对日常的过程质量进 行控制。※
6
之间存在较大差别时表示有特殊原因存在。
双边公差的过程指数
1. CP能力指数（过程位于中心）： 2. CPK能力指数（过程不位于中心）：
C MIN(CPL,CPU) PK
3. PP性能指数（过程位于中心）： 4. PPK性能指数（过程不位于中心）：
P MIN(PPL, PPU) PK
CPK≤CP PPK≤PP
过程相对稳定系数评价
1. 过程稳定系数：
2. 相对稳定系数：
过程相对稳定系数 drσ ＜10%
10%≤ drσ ＜20% 20%≤ drσ ＜50%
drσ ≥50%
评价 接近稳定 不太稳定
不稳定 很不稳定
6西格玛相关
（一）连续型数据的流程能力
流程的西格玛水平：Z值 Z值可以描述流程的不合格率P(d)