直接插入排序、直接选择排序、堆排序、快速排序、冒泡排序的实验报告
排序实验报告_排序综合实验报告材料

班级
2*10^7
10 电信 1 班
10^8
操作系统
10^5
Microsoft Windows 7 旗舰版 (64 位/Service Pck 1)
正序
xxxxxxxxxxxxx
逆序
编译软件
直接插入
Visul C++ 6.0
(带监视哨〕
emil
C
609803959.
24.874
10^4
100.158
2*10^4
中选出键值最小的记录,与无序区第一个记录 R 交换;新的无序区为 R 到
各种排序试验结果:
R[n],从中再选出键值最小的记录,与无序区第一个记录 R 交换;类似, CPU
第 i 趟排序时 R 到 R[i-1]是有序区,无序区为 R[i]到 R[n],从中选出键
(英特尔)Intel(R) Core(TM) i5 CPU M 480 2.67GHz
〔1〕二路并归排序:开始时,将排序表 R 到 R[n]看成 n 个长度为 1
录,顺序放在已排好序的子序列的后面〔或最前〕,直到全部记录排序完 的有序子表,把这些子表两两并归,便得到 n/2 个有序的子表〔当 n 为奇
毕。
数时,并归后仍是有一个长度为 1 的子表〕;然后,再把这 n/2 个有序的
〔1〕直接选择排序:首先,全部记录组成初始无序区 R 到 R[n],从 子表两两并归,如此反复,直到最终得到一个程度为 n 的有序表为止。
指导老师: 胡圣荣
序与排序要求相反时就交换两者的位置,直到没有反序的记录为止。
日期: 20XX.12.15~20XX.1.5
〔1〕冒泡排序:设想排序表 R 到 R[n]垂直放置,将每个记录 R[i]看
数据结构课程设报告—各种排序算法的比较

数据结构课程设计报告几种排序算法的演示1、需求分析:运行环境:Microsoft Visual Studio 20052、程序实现功能:3、通过用户键入的数据, 经过程序进行排序, 最后给予数据由小到大的输出。
排序的方式包含教材中所介绍的几种常用的排序方式:直接插入排序、折半插入排序、冒泡排序、快速排序、选择排序、堆排序、归并排序。
每种排序过程中均显示每一趟排序的细节。
程序的输入:输入所需排序方式的序号。
输入排序的数据的个数。
输入具体的数据元素。
程序的输出:输出排序每一趟的结果, 及最后排序结果1、设计说明:算法设计思想:a交换排序(冒泡排序、快速排序)交换排序的基本思想是: 对排序表中的数据元素按关键字进行两两比较, 如果发生逆序(即排列顺序与排序后的次序正好相反), 则两者交换位置, 直到所有数据元素都排好序为止。
b插入排序(直接插入排序、折半插入排序)插入排序的基本思想是: 每一次设法把一个数据元素插入到已经排序的部分序列的合适位置, 使得插入后的序列仍然是有序的。
开始时建立一个初始的有序序列, 它只包含一个数据元素。
然后, 从这个初始序列出发不断插入数据元素, 直到最后一个数据元素插到有序序列后, 整个排序工作就完成了。
c选择排序(简单选择排序、堆排序)选择排序的基本思想是: 第一趟在有n个数据元素的排序表中选出关键字最小的数据元素, 然后在剩下的n-1个数据元素中再选出关键字最小(整个数据表中次小)的数据元素, 依次重复, 每一趟(例如第i趟, i=1, …, n-1)总是在当前剩下的n-i+1个待排序数据元素中选出关键字最小的数据元素, 作为有序数据元素序列的第i个数据元素。
等到第n-1趟选择结束, 待排序数据元素仅剩下一个时就不用再选了, 按选出的先后次序所得到的数据元素序列即为有序序列, 排序即告完成。
d归并排序(两路归并排序)1、两路归并排序的基本思想是: 假设初始排序表有n个数据元素, 首先把它看成是长度为1的首尾相接的n个有序子表(以后称它们为归并项), 先做两两归并, 得n/2上取整个长度为2的归并项(如果n为奇数, 则最后一个归并项的长度为1);再做两两归并, ……, 如此重复, 最后得到一个长度为n的有序序列。
快速排序算法实验报告

快速排序算法实验报告快速排序一、问题描述在操作系统中,我们总是希望以最短的时间处理完所有的任务。
但事情总是要一件件地做,任务也要操作系统一件件地处理。
当操作系统处理一件任务时,其他待处理的任务就需要等待。
虽然所有任务的处理时间不能降低,但我们可以安排它们的处理顺序,将耗时少的任务先处理,耗时多的任务后处理,这样就可以使所有任务等待的时间和最小。
只需要将n 件任务按用时去从小到大排序,就可以得到任务依次的处理顺序。
当有 n 件任务同时来临时,每件任务需要用时ni,求让所有任务等待的时间和最小的任务处理顺序。
二、需求分析1. 输入事件件数n,分别随机产生做完n件事所需要的时间;2. 对n件事所需的时间使用快速排序法,进行排序输出。
排序时,要求轴值随机产生。
3. 输入输出格式:输入:第一行是一个整数n,代表任务的件数。
接下来一行,有n个正整数,代表每件任务所用的时间。
输出:输出有n行,每行一个正整数,从第一行到最后一行依次代表着操作系统要处理的任务所用的时间。
按此顺序进行,则使得所有任务等待时间最小。
4. 测试数据:输入 95 3 4 26 1 57 3 输出1 2 3 3 4 5 5 6 7三、概要设计抽象数据类型因为此题不需要存储复杂的信息,故只需一个整型数组就可以了。
算法的基本思想对一个给定的进行快速排序,首先需要选择一个轴值,假设输入的数组中有k个小于轴值的数,于是这些数被放在数组最左边的k个位置上,而大于周知的结点被放在数组右边的n-k个位置上。
k也是轴值的下标。
这样k把数组分成了两个子数组。
分别对两个子数组,进行类似的操作,便能得到正确的排序结果。
程序的流程输入事件件数n-->随机产生做完没个事件所需时间-->对n个时间进行排序-->输出结果快速排序方法:初始状态 72 6 57 88 85 42 l r第一趟循环 72 6 57 88 85 42 l r 第一次交换 6 72 57 88 85 42 l r 第二趟循环 6 72 57 88 85 42 r l 第二次交换 72 6 57 88 85 42 r l反转交换 6 72 57 88 85 42 r l这就是依靠轴值,将数组分成两部分的实例。
常见算法设计实验报告(3篇)

第1篇一、实验目的通过本次实验,掌握常见算法的设计原理、实现方法以及性能分析。
通过实际编程,加深对算法的理解,提高编程能力,并学会运用算法解决实际问题。
二、实验内容本次实验选择了以下常见算法进行设计和实现:1. 排序算法:冒泡排序、选择排序、插入排序、快速排序、归并排序、堆排序。
2. 查找算法:顺序查找、二分查找。
3. 图算法:深度优先搜索(DFS)、广度优先搜索(BFS)、最小生成树(Prim算法、Kruskal算法)。
4. 动态规划算法:0-1背包问题。
三、实验原理1. 排序算法:排序算法的主要目的是将一组数据按照一定的顺序排列。
常见的排序算法包括冒泡排序、选择排序、插入排序、快速排序、归并排序和堆排序等。
2. 查找算法:查找算法用于在数据集中查找特定的元素。
常见的查找算法包括顺序查找和二分查找。
3. 图算法:图算法用于处理图结构的数据。
常见的图算法包括深度优先搜索(DFS)、广度优先搜索(BFS)、最小生成树(Prim算法、Kruskal算法)等。
4. 动态规划算法:动态规划算法是一种将复杂问题分解为子问题,通过求解子问题来求解原问题的算法。
常见的动态规划算法包括0-1背包问题。
四、实验过程1. 排序算法(1)冒泡排序:通过比较相邻元素,如果顺序错误则交换,重复此过程,直到没有需要交换的元素。
(2)选择排序:每次从剩余元素中选取最小(或最大)的元素,放到已排序序列的末尾。
(3)插入排序:将未排序的数据插入到已排序序列中适当的位置。
(4)快速排序:选择一个枢纽元素,将序列分为两部分,使左侧不大于枢纽,右侧不小于枢纽,然后递归地对两部分进行快速排序。
(5)归并排序:将序列分为两半,分别对两半进行归并排序,然后将排序好的两半合并。
(6)堆排序:将序列构建成最大堆,然后重复取出堆顶元素,并调整剩余元素,使剩余元素仍满足最大堆的性质。
2. 查找算法(1)顺序查找:从序列的第一个元素开始,依次比较,直到找到目标元素或遍历完整个序列。
偏爱排序实验报告

一、实验背景随着计算机技术的不断发展,数据量的激增使得排序算法在数据处理中扮演着越来越重要的角色。
为了提高数据处理效率,选择合适的排序算法至关重要。
本实验旨在通过实际操作,对比分析不同排序算法的性能,以确定在特定情况下最偏爱的排序算法。
二、实验目的1. 掌握常用排序算法的原理和实现方法;2. 分析不同排序算法的时间复杂度和空间复杂度;3. 比较不同排序算法在实际应用中的性能差异;4. 确定在特定情况下最偏爱的排序算法。
三、实验内容本次实验选取了以下排序算法进行对比分析:1. 直接插入排序;2. 冒泡排序;3. 快速排序;4. 归并排序;5. 希尔排序;6. 简单选择排序;7. 堆排序;8. 基数排序。
实验过程中,采用以下步骤:1. 编写C语言程序,实现上述排序算法;2. 对随机生成的测试数据进行排序,并记录排序时间;3. 分析不同排序算法的时间复杂度和空间复杂度;4. 对比不同排序算法在实际应用中的性能差异。
四、实验结果与分析1. 直接插入排序:时间复杂度为O(n^2),空间复杂度为O(1)。
当数据量较小时,插入排序具有较好的性能,但数据量较大时,性能较差。
2. 冒泡排序:时间复杂度为O(n^2),空间复杂度为O(1)。
冒泡排序简单易实现,但效率较低,不适用于大数据量排序。
3. 快速排序:平均时间复杂度为O(nlogn),最坏时间复杂度为O(n^2),空间复杂度为O(logn)。
快速排序在大多数情况下具有较好的性能,但最坏情况下性能较差。
4. 归并排序:时间复杂度为O(nlogn),空间复杂度为O(n)。
归并排序在所有情况下都具有稳定的性能,但空间复杂度较高。
5. 希尔排序:时间复杂度介于O(n)和O(n^2)之间,空间复杂度为O(1)。
希尔排序是插入排序的改进版,适用于数据量较大且基本有序的情况。
6. 简单选择排序:时间复杂度为O(n^2),空间复杂度为O(1)。
简单选择排序简单易实现,但效率较低,不适用于大数据量排序。
数据结构(C语言版)实验报告 (内部排序算法比较)

《数据结构与算法》实验报告一、需求分析问题描述:在教科书中,各种内部排序算法的时间复杂度分析结果只给出了算法执行时间的阶,或大概执行时间。
试通过随机数据比较各算法的关键字比较次数和关键字移动次数,以取得直观感受。
基本要求:(l)对以下6种常用的内部排序算法进行比较:起泡排序、直接插入排序、简单选择排序、快速排序、希尔排序、堆排序。
(2)待排序表的表长不小于100000;其中的数据要用伪随机数程序产生;至少要用5组不同的输入数据作比较;比较的指标为有关键字参加的比较次数和关键字的移动次数(关键字交换计为3次移动)。
(3)最后要对结果作简单分析,包括对各组数据得出结果波动大小的解释。
数据测试:二.概要设计1.程序所需的抽象数据类型的定义:typedef int BOOL; //说明BOOL是int的别名typedef struct StudentData { int num; //存放关键字}Data; typedef struct LinkList { int Length; //数组长度Data Record[MAXSIZE]; //用数组存放所有的随机数} LinkList int RandArray[MAXSIZE]; //定义长度为MAXSIZE的随机数组void RandomNum() //随机生成函数void InitLinkList(LinkList* L) //初始化链表BOOL LT(int i, int j,int* CmpNum) //比较i和j 的大小void Display(LinkList* L) //显示输出函数void ShellSort(LinkList* L, int dlta[], int t,int* CmpNum, int* ChgNum) //希尔排序void QuickSort (LinkList* L, int* CmpNum, int* ChgNum) //快速排序void HeapSort (LinkList* L, int* CmpNum, int* ChgNum) //堆排序void BubbleSort(LinkList* L, int* CmpNum, int* ChgNum) //冒泡排序void SelSort(LinkList* L, int* CmpNum, int* ChgNum) //选择排序void Compare(LinkList* L,int* CmpNum, int* ChgNum) //比较所有排序2 .各程序模块之间的层次(调用)关系:二、详细设计typedef int BOOL; //定义标识符关键字BOOL别名为int typedef struct StudentData //记录数据类型{int num; //定义关键字类型}Data; //排序的记录数据类型定义typedef struct LinkList //记录线性表{int Length; //定义表长Data Record[MAXSIZE]; //表长记录最大值}LinkList; //排序的记录线性表类型定义int RandArray[MAXSIZE]; //定义随机数组类型及最大值/******************随机生成函数********************/void RandomNum(){int i; srand((int)time(NULL)); //用伪随机数程序产生伪随机数for(i=0; i小于MAXSIZE; i++) RandArray[i]<=(int)rand(); 返回;}/*****************初始化链表**********************/void InitLinkList(LinkList* L) //初始化链表{int i;memset(L,0,sizeof(LinkList));RandomNum();for(i=0; i小于<MAXSIZE; i++)L->Record[i].num<=RandArray[i]; L->Length<=i;}BOOL LT(int i, int j,int* CmpNum){(*CmpNum)++; 若i<j) 则返回TRUE; 否则返回FALSE;}void Display(LinkList* L){FILE* f; //定义一个文件指针f int i;若打开文件的指令不为空则//通过文件指针f打开文件为条件判断{ //是否应该打开文件输出“can't open file”;exit(0); }for (i=0; i小于L->Length; i++)fprintf(f,"%d\n",L->Record[i].num);通过文件指针f关闭文件;三、调试分析1.调试过程中遇到的问题及经验体会:在本次程序的编写和调试过程中,我曾多次修改代码,并根据调试显示的界面一次次调整代码。
关于算法的实验报告(3篇)

第1篇一、实验目的1. 理解快速排序算法的基本原理和实现方法。
2. 掌握快速排序算法的时间复杂度和空间复杂度分析。
3. 通过实验验证快速排序算法的效率。
4. 提高编程能力和算法设计能力。
二、实验环境1. 操作系统:Windows 102. 编程语言:C++3. 开发工具:Visual Studio 2019三、实验原理快速排序算法是一种分而治之的排序算法,其基本思想是:选取一个基准元素,将待排序序列分为两个子序列,其中一个子序列的所有元素均小于基准元素,另一个子序列的所有元素均大于基准元素,然后递归地对这两个子序列进行快速排序。
快速排序算法的时间复杂度主要取决于基准元素的选取和划分过程。
在平均情况下,快速排序的时间复杂度为O(nlogn),但在最坏情况下,时间复杂度会退化到O(n^2)。
四、实验内容1. 快速排序算法的代码实现2. 快速排序算法的时间复杂度分析3. 快速排序算法的效率验证五、实验步骤1. 设计快速排序算法的C++代码实现,包括以下功能:- 选取基准元素- 划分序列- 递归排序2. 编写主函数,用于生成随机数组和测试快速排序算法。
3. 分析快速排序算法的时间复杂度。
4. 对不同规模的数据集进行测试,验证快速排序算法的效率。
六、实验结果与分析1. 快速排序算法的代码实现```cppinclude <iostream>include <vector>include <cstdlib>include <ctime>using namespace std;// 生成随机数组void generateRandomArray(vector<int>& arr, int n) {srand((unsigned)time(0));for (int i = 0; i < n; ++i) {arr.push_back(rand() % 1000);}}// 快速排序void quickSort(vector<int>& arr, int left, int right) { if (left >= right) {return;}int i = left;int j = right;int pivot = arr[(left + right) / 2]; // 选取中间元素作为基准 while (i <= j) {while (arr[i] < pivot) {i++;}while (arr[j] > pivot) {j--;}if (i <= j) {swap(arr[i], arr[j]);i++;j--;}}quickSort(arr, left, j);quickSort(arr, i, right);}int main() {int n = 10000; // 测试数据规模vector<int> arr;generateRandomArray(arr, n);clock_t start = clock();quickSort(arr, 0, n - 1);clock_t end = clock();cout << "排序用时:" << double(end - start) / CLOCKS_PER_SEC << "秒" << endl;return 0;}```2. 快速排序算法的时间复杂度分析根据实验结果,快速排序算法在平均情况下的时间复杂度为O(nlogn),在最坏情况下的时间复杂度为O(n^2)。
排序算法实验报告
数据结构实验报告八种排序算法实验报告一、实验内容编写关于八种排序算法的C语言程序,要求包含直接插入排序、希尔排序、简单项选择择排序、堆排序、冒泡排序、快速排序、归并排序和基数排序。
二、实验步骤各种内部排序算法的比较:1.八种排序算法的复杂度分析〔时间与空间〕。
2.八种排序算法的C语言编程实现。
3.八种排序算法的比较,包括比较次数、移动次数。
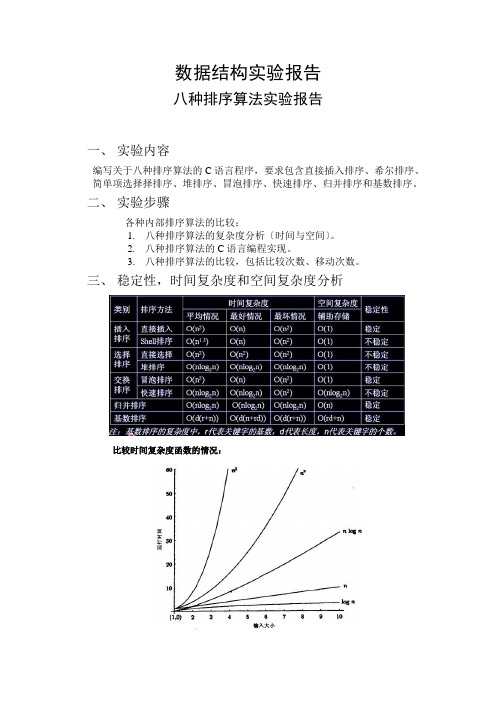
三、稳定性,时间复杂度和空间复杂度分析比较时间复杂度函数的情况:时间复杂度函数O(n)的增长情况所以对n较大的排序记录。
一般的选择都是时间复杂度为O(nlog2n)的排序方法。
时间复杂度来说:(1)平方阶(O(n2))排序各类简单排序:直接插入、直接选择和冒泡排序;(2)线性对数阶(O(nlog2n))排序快速排序、堆排序和归并排序;(3)O(n1+§))排序,§是介于0和1之间的常数。
希尔排序(4)线性阶(O(n))排序基数排序,此外还有桶、箱排序。
说明:当原表有序或基本有序时,直接插入排序和冒泡排序将大大减少比较次数和移动记录的次数,时间复杂度可降至O〔n〕;而快速排序则相反,当原表基本有序时,将蜕化为冒泡排序,时间复杂度提高为O〔n2〕;原表是否有序,对简单项选择择排序、堆排序、归并排序和基数排序的时间复杂度影响不大。
稳定性:排序算法的稳定性:假设待排序的序列中,存在多个具有相同关键字的记录,经过排序,这些记录的相对次序保持不变,则称该算法是稳定的;假设经排序后,记录的相对次序发生了改变,则称该算法是不稳定的。
稳定性的好处:排序算法如果是稳定的,那么从一个键上排序,然后再从另一个键上排序,第一个键排序的结果可以为第二个键排序所用。
基数排序就是这样,先按低位排序,逐次按高位排序,低位相同的元素其顺序再高位也相同时是不会改变的。
另外,如果排序算法稳定,可以防止多余的比较;稳定的排序算法:冒泡排序、插入排序、归并排序和基数排序不是稳定的排序算法:选择排序、快速排序、希尔排序、堆排序四、设计细节排序有内部排序和外部排序,内部排序是数据记录在内存中进行排序,而外部排序是因排序的数据很大,一次不能容纳全部的排序记录,在排序过程中需要访问外存。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
姓名
学号
实验组
实验时间
指导教师
成绩
实验项目名称
实验目的
1.熟练掌握顺序表和有序表的查找方法。
2.熟悉静态查找树的构造方法和查找算法,熟练掌握二叉排序树的构造方法和查找算法。
3.掌握描述查找过程的判定树的构造方法,掌握各种查找方法在等概率情况下查找成功时的平均查找长度。
实验步骤
1、确定数据的结构
2、编写头文件、函数及变量声明
3、设计子函数
4、写主函数,并调用子函数
5、调试编写好的程序
6、编译正确后,运行,观察分析结果
实验内容
程序1内部排序算法比较
[问题描述]
编写常用的排序算法,并编写主程序测试。
[基本要求]
(1)对以下常用的6种排序算法进行比较:直接插入排序、直接选择排序、堆排序、快速排序、冒泡排序。
}
}
}
堆排序
void CreatHeap(ElemType A[], int n)
{
int i;
for( i = (n–2)/2; i >= 0; i--)
Sift(A, n, i); //调整A[i..n-1]使之为一个堆
}
void Sift(ElemType A[], int n, int i)
while ( i<=j ) {
while ( i<=j && A[i].stn <= x.stn ) i++; //从左到右
while ( i<=j && A[j].stn >= x.stn ) j--; //从右到左if ( i < j ) {
temp=A[i]; A[i]=A[j]; A[j]=temp;i++; j--;
ElemType x;
for ( i=0; i<=n-2; i++ )
{ //每一趟选择最小元素并与A[i]交换
k=i;
for (j=i+1; j<=n-1; j++) //查找最小元素的下标
if (A[j].stn <A[k].stn ) k=j;
if (k!=i) { //交换
x=A[i]; A[i]=A[k]; A[k]=x;
A[0] = A[i];
A[i] = x;
Sift(A, i, 0);//调整A[0..i-1]使之为一个堆
}
}
//冒泡排序
voidBubbleSort( ElemType A[],intn )
{
inti, j, flag;//flag为交换标记
ElemType x;
for(i=1; i<=n-1; i++) {//最多n-1趟排序
typedefintElemType;
//直接插入排序
voidInsertSort ( ElemType A[],intn )
{
inti, j;
ElemType x;
for( i=1; i<n; i++ ){//进行n-1次插入
x = A[i];//准备插入第i个元素
for( j=i-1; j>=0; j-- ){//从第i-1个开始往前找插入点
{
int i, j, flag; //flag为交换标记
ElemType x;
for (i=1; i<=n-1; i++) { //最多n-1趟排序
flag=0; //假设本次没有交换
for (j=n-1; j>=i; j--)//第i趟
if ( A[j].stn < A[j-1].stn ) {
flag=1; //出现交换
flag=0;//假设本次没有交换
for(j=n-1; j>=i; j--)//第i趟
if( A[j]< A[j-1]) {
flag=1;//出现交换
x=A[j]; A[j]=A[j-1]; A[j-1]=x;
}
if(flag==0)return;
}
}
//快速排序
voidQuickSort(ElemType A[],ints,intt)
InsertSort (A, N );
for(i=0;i<N;i++)
cout<<A[i]<<endl;
运//运行结果如右;
cout<<"直接选择排序:"<<endl;
SelectSort(A, N);
for(i=0;i<N;i++)
cout<<A[i]<<endl;
cout<<"堆排序:"<<endl;
HeapSort(A, N);
for(i=0;i<N;i++)
cout<<A[i]<<endl;
cout<<"冒泡排序:"<<endl;
BubbleSort(A, N);
for(i=0;i<N;i++)
cout<<A[i]<<endl;
cout<<"快速排序:"<<endl;
QuickSort(A,0,1);
{ //调整A[i..n-1]成为一个堆(它的左右子树已是一个堆)
ElemType x=A[i];
int j = 2 * i + 1; // j为i的左孩子
while (j <= n-1) { // i有左子树
if ( j +1 < n && A[j].stn < A[j+1].stn )
j++; //使j指向左右孩子中排序码大的孩子
for(i=0;i<N;i++)
cout<<A[i]<<endl;
}
实验总结
指导教师意见
签名:年月日
注:各学院可根据教学需要对以上栏木进行增减。表格内容可根据内容扩充。
k=i;
for(j=i+1; j<=n-1; j++)//查找最小元素的下标
if(A[j]<A[k]) k=j;
if(k!=i) {//交换
x=A[i]; A[i]=A[k]; A[k]=x;
}
}
}
//堆排序
voidSift(ElemType A[],intn,inti);
voidCreatHeap(ElemType A[],intn)
}
voidmain(){
inti,j,n,N=5;
cout<<"请输入个整数:";
ElemType A[5];
for(j=0;j<N;j++)
cin>>A[j];
cout<<"排序前为:"<<endl;
for(i=0;i<N;i++)
cout<<A[i]<<endl;
cout<<"直接插入排序:"<<endl;
(2)待排序表的表长不小于100;其中的数据用自行设计。
(3)对结果作出分析。
直接插入排序
void InsertSort ( ElemType A[], int n )
{
int i, j;
ElemType x;
for ( i=1; i<n; i++ ) { //进行n-1次插入
x = A[i]; //准备插入第i个元素
实验要求
1.了解散列表的构造和查找算法。
2.了解各种排序方法的执行过程及其所依据的原则,掌握各种排序方法时间复杂度的分析方法。
3.熟练掌握希尔排序、快速排序、堆排序等高效排序算法。
实验原理
在visual c++编程环境中编写程序源代码,并编译、运行程序结果
实验仪器
奔腾2计算机或以上机型、visual c++编程环境
if( x< A[j] )
A[j+1]=A[j];
else
break;
}
A[j+1]=x;//插入
}
}
//直接选择排序
voidSelectSort(ElemType A[],intn)
{
inti, j, k;
ElemType x;
for( i=0; i<=n-2; i++ )
{//每一趟选择最小元素并与A[i]交换
{
inti;
for( i = (n-2)/2; i >= 0; i--)
Sift(A, n, i);//调整A[i..n-1]使之为一个堆
}
voidSift(ElemType A[],intn,inti)
{//调整A[i..n-1]成为一个堆(它的左右子树已是一个堆)
ElemType x=A[i];
x=A[j]; A[j]=A[j-1]; A[j-1]=x;
}
if (flag==0) return;
}
}
快速排序
void QuickSort(ElemType A[ ], int s, int t)
{ //递归算法,对区间A[s]~A[t]进行快速排序
