离散数学(祝清顺,贾立新,刘楠 编著)思维导图
合集下载
离散数学ppt课件
02
集合论基础
集合的基本概念
总结词
集合是离散数学中的基本概念， 是研究离散对象的重要工具。
详细描述
集合是由一组确定的、互不相同 的、可区分的对象组成的整体。 这些对象称为集合的元素。例如 ，自然数集、平面上的点集等。
集合的运算和性质
总结词
集合的运算和性质是离散数学中的重要内容，包括集合的交、并、差、补等基本运算，以及集合的确定性、互异 性、无序性等性质。
生，1表示事件一定会发生。
离散概率论的运算和性质
概率的加法性质
如果两个事件A和B是互斥的，那么P(A或B)等于P(A)加上 P(B)。
概率的乘法性质
如果事件A和B是独立的，那么P(A和B)等于P(A)乘以P(B) 。
全概率公式
对于任意的事件A，存在一个完备事件组{E1, E2, ..., En}， 使得P(Ai)>0 (i=1,2,...,n)，且E1∪E2∪...∪En=S，那么 P(A)=∑[i=1 to n] P(Ai)P(A|Ei)。
工程学科
离散数学在工程学科中也有着重要的 应用，如计算机通信网络、控制系统 、电子工程等领域。
离散数学的重要性
基础性
离散数学是数学的一个重要分支 ，是学习其他数学课程的基础。
应用性
离散数学在各个领域都有着广泛的 应用，掌握离散数学的知识和方法 对于解决实际问题具有重要的意义 。
培养逻辑思维
学习离散数学可以培养人的逻辑思 维能力和问题解决能力，对于个人 的思维发展和职业发展都有很大的 帮助。
详细描述
邻接矩阵是一种常用的表示图的方法，它是 一个二维矩阵，其中行和列对应于图中的节 点，如果两个节点之间存在一条边，则矩阵 中相应的元素为1，否则为0。邻接表是一 种更有效的表示图的方法，它使用链表来存 储与每个节点相邻的节点。
第一章命题逻辑知识地图
《离散数学》知识地图第一章命题逻辑第一节命题与联结词命题的概念：能判断真假的陈述句称为命题。
命题的真值：一个命题的真或假称为命题的真值。
真用T或1表示，假用F或0表示。
原子命题：不能再分解为其他命题的命题称为原子命题。
复合命题：由原子命题与命题联结词构成的命题称为复合命题。
命题标识符：表示原子命题的符号称为命题标识符，常用大写字母、带下标的大写字母。
命题常元：一个表示确定命题的命题标识符。
命题变元：一个能指代任意命题的命题标识符。
五个命题联结词：否定⌝，合取∧，析取∨，条件→和双条件联结词↔。
命题符号化：目的在于用五个联结词将日常语言中的命题转化为数理逻辑中的形式命题，其关键在于对自然语言中语句之间的逻辑关系以及命题联结词的含义要有正确的理解，使用适当的联结词。
第二节命题公式、翻译与真值表命题公式：（1）一个命题变元是一个命题公式；（2）若A是一个命题公式，则⌝A也是一个命题公式；（3）若A、B是命题公式，则A∧B、A∨B、A→B和A↔B均为命题公式；（4）只有经过有限次地应用（1）、（2）、（3）所得的结果才是命题公式。
子公式：若命题公式B是命题公式A的一部分，则称B是A的子公式。
真值指派：设A是一个命题公式，P1，P2，…，P n是出现在A中的所有命题变元。
给P1，P2，…，P n指定一组真值，称为对公式A的一个真值指派（或解释或赋值）。
若指定的一组真值使A为真，则称这组值为成真指派，否则称之为成假指派。
真值表：一个命题公式A的真值表的左上角部分是A的所有命题变元，左下角部分是这些命题变元的所有可能的指派，右上角一般是公式A本身，右下角是A在对应指派下的真值。
五个常用联结词的真值表：第三节公式分类与等价式公式分类：永真式、永假式和可满足式。
永真式（重言式）：一个命题公式A，若对A所有可能的真值指派（解释），（1）A都为真，则称A为永真式（重言式）。
（2）A都为假，则称A为永假式（矛盾式）。
（3）至少存在一个真值指派使A为真，则称A为可满足式。
离散数学-第11章
离散数学讲义之
图 论
主讲:熊焕亮
图论简介
• 图论（graph theory）是研究节点和边组成的图 形的数学理论和方法，为离散数学的一个重要分 支。图论的基本元素是节点和边（也称线、弧、 枝），用节点表示所研究的对象，用边表示研究 对象之间的某种特定关系。因此，图论可用节点 和边组成的图形及其有关的理论和方法来描述、 分析和解决各种实际问题，已广泛地应用于物理、 化学、运筹学、计算机科学、电子学、信息论、 控制论、网络理论、管理科学、社会科学等几乎 所有学科领域的有关问题。图论与组合数学、线 性规划、群论、矩阵论、概率论、数值分析等数 学分支有密切的关系。
均为偶数，所以 d (v)为偶数，但因中顶点度数为奇数，
vV1
vV1
d (v ) d (v )
vV2
所以 | V1 |必为偶数。
14
11.1.2 简单图、多重图和同构图
V {v1 , v2 ,., vn } 设 G V , E 为一个阶无向图， 称 d (v1 ), d (v2 )d (vn ),为 G 的度数列。对于顶点标定的无向图，它的度数列是唯一的。反之， 对于给定的非负整数列d (d1 , d 2 ,d n )，若存在以 V (v1 , v2 ,, vn ) 为顶点 集的n阶无向图G,使得 d (vi ) d i ，则称d是可图化的。特别地，若所得 的图是简单图,则称d是可简单图化的。 例11.1.2 （1）（3，5，1，4），（1，2，3，4，5）能成为图的度 数列吗？为什么？ （2）已知图G 中有15条边，2个度数为4的结点，4个度数为3的结点， 其余结点度数均小于等于2，问G 中至少有多少个结点？为什么？ 解 （1）由于给定的两个度数列中奇度顶点个数均为奇数，由上述 推论可知，他们都不能成为图的度数列。 （2）图中边数为15，由握手定理可知，G 中所有结点度数和为30。 除去2个度数为4的结点和4个度数为3的结点，还剩下10度。其余结 点度数小于等于2，假设均为2，则至少要5个结点，所以总共至少要1 1个结点。
图 论
主讲:熊焕亮
图论简介
• 图论（graph theory）是研究节点和边组成的图 形的数学理论和方法，为离散数学的一个重要分 支。图论的基本元素是节点和边（也称线、弧、 枝），用节点表示所研究的对象，用边表示研究 对象之间的某种特定关系。因此，图论可用节点 和边组成的图形及其有关的理论和方法来描述、 分析和解决各种实际问题，已广泛地应用于物理、 化学、运筹学、计算机科学、电子学、信息论、 控制论、网络理论、管理科学、社会科学等几乎 所有学科领域的有关问题。图论与组合数学、线 性规划、群论、矩阵论、概率论、数值分析等数 学分支有密切的关系。
均为偶数，所以 d (v)为偶数，但因中顶点度数为奇数，
vV1
vV1
d (v ) d (v )
vV2
所以 | V1 |必为偶数。
14
11.1.2 简单图、多重图和同构图
V {v1 , v2 ,., vn } 设 G V , E 为一个阶无向图， 称 d (v1 ), d (v2 )d (vn ),为 G 的度数列。对于顶点标定的无向图，它的度数列是唯一的。反之， 对于给定的非负整数列d (d1 , d 2 ,d n )，若存在以 V (v1 , v2 ,, vn ) 为顶点 集的n阶无向图G,使得 d (vi ) d i ，则称d是可图化的。特别地，若所得 的图是简单图,则称d是可简单图化的。 例11.1.2 （1）（3，5，1，4），（1，2，3，4，5）能成为图的度 数列吗？为什么？ （2）已知图G 中有15条边，2个度数为4的结点，4个度数为3的结点， 其余结点度数均小于等于2，问G 中至少有多少个结点？为什么？ 解 （1）由于给定的两个度数列中奇度顶点个数均为奇数，由上述 推论可知，他们都不能成为图的度数列。 （2）图中边数为15，由握手定理可知，G 中所有结点度数和为30。 除去2个度数为4的结点和4个度数为3的结点，还剩下10度。其余结 点度数小于等于2，假设均为2，则至少要5个结点，所以总共至少要1 1个结点。
离散数学 第4章 代数系统(祝清顺版)
离散数学 第四章 代数系统 2007年8月20日
代数结构的知识体系
半群与群 环与域 格与布尔代数
分类 成分：载体及运算 公理：运算性质 产生 代数系统的构成
子集
子代数
同 种 的 同 类 型 的
等价关系
映射
代数系统的 同态与同构 代数系统间的关系
离散数学 第四章 代数系统 2007年8月20日
商代数 新代数系统
，有限域理论是差错控制编码理论的数学基础，在通讯中发 挥了重要作用。而电子线路设计、电子计算机硬件设计和通 讯系统设计更是离不开布尔代数。
离散数学 第四章 代数系统 2007年8月20日
学习本篇的方法
1、要按照数学的思维方式学习, 即观察客观世界, 抽象出模型 , 再分析、推理揭示内在规律的过程。 2、领会“抽象”性：代数的抽象性不仅体现在元素的抽象上, 还体现在相应运算的抽象上, 是在最纯粹的形式下研究代数结 构中的运算的规律与性质, 从运算的角度来考虑代数结构中的 元素。因此, 初等代数的相应概念、结论不能直接应用在抽象 代数中。如何跨越从直观到抽象是学习抽象代数的重要一步。 3、教材的基本思路是： 首先严格定义什么是代数结构, 并讨 论一般代数结构的基本性质。然后讨论代数结构研究的两个方 面：其一是通过一些基本性质来规定一类特定的代数结构, 并 对这类代数结构的性质进行研究。其二是研究代数结构之间的 各种关系, 通过对代数结构之间关系的研究 , 就可以把一个代 数结构中的某些性质推广到另一个代数结构中。
离散数学
第四章 代数系统
2007年8月20日
例题
例2 实数集R和两个二元运算: 普通加法＋和普通乘法 ×, 构成一代数系统, 记作(R, ＋, ×).
(1) 载体是实数集R.
代数结构的知识体系
半群与群 环与域 格与布尔代数
分类 成分：载体及运算 公理：运算性质 产生 代数系统的构成
子集
子代数
同 种 的 同 类 型 的
等价关系
映射
代数系统的 同态与同构 代数系统间的关系
离散数学 第四章 代数系统 2007年8月20日
商代数 新代数系统
，有限域理论是差错控制编码理论的数学基础，在通讯中发 挥了重要作用。而电子线路设计、电子计算机硬件设计和通 讯系统设计更是离不开布尔代数。
离散数学 第四章 代数系统 2007年8月20日
学习本篇的方法
1、要按照数学的思维方式学习, 即观察客观世界, 抽象出模型 , 再分析、推理揭示内在规律的过程。 2、领会“抽象”性：代数的抽象性不仅体现在元素的抽象上, 还体现在相应运算的抽象上, 是在最纯粹的形式下研究代数结 构中的运算的规律与性质, 从运算的角度来考虑代数结构中的 元素。因此, 初等代数的相应概念、结论不能直接应用在抽象 代数中。如何跨越从直观到抽象是学习抽象代数的重要一步。 3、教材的基本思路是： 首先严格定义什么是代数结构, 并讨 论一般代数结构的基本性质。然后讨论代数结构研究的两个方 面：其一是通过一些基本性质来规定一类特定的代数结构, 并 对这类代数结构的性质进行研究。其二是研究代数结构之间的 各种关系, 通过对代数结构之间关系的研究 , 就可以把一个代 数结构中的某些性质推广到另一个代数结构中。
离散数学
第四章 代数系统
2007年8月20日
例题
例2 实数集R和两个二元运算: 普通加法＋和普通乘法 ×, 构成一代数系统, 记作(R, ＋, ×).
(1) 载体是实数集R.
离散数学第2章 关系(祝清顺版)
第二章 二元关系 2007年8月20日
离散数学
关系矩阵的实例
例9 设A={3, 5, 6, 9}, A上的二元关系
R={<x, y｜x＞y},
试求出关系矩阵。
[解] 关系的集合表示为:
R＝{9, 3, 9, 5, 9, 6, 6, 3, 6, 5, 5, 3}.
关系矩阵为: 0 1 MR= 1 1
关系的三种表示方法： 集合表达式 关系矩阵
关系图
关系矩阵和关系图可以表示有限集合上的关系。
离散数学
第二章 二元关系
2007年8月20日
关系矩阵
设给定集合A={a1,a2,…,an}，B={b1,b2,…,bm}，R为从A到B
的一个二元关系，构造一个n×m矩阵。用集合A的元素标注矩
阵的行，用集合B的元素标注矩阵的列，对于aiA和bjB，令
n2 n2
个. 不
每一个子集代表一个A上的二元关系，所以A上有 2 同的二元关系。 |Ai|=mi，则A1×A2×…×An上有 2 二元关系。
离散数学 第二章 二元关系 2007年8月20日
m1m2…mn
个不同的
常用的关系
定义 对任意集合A，定义 (1) 空关系 (2) 全域关系 EA={<x, y>|x∈A且y∈A}=A×A (3) 恒等关系 IA={<x, x>|x∈A} (4) 小于或等于关系：LA={<x, y>|x, y∈A且x≤y}, 其中 AR。 (5) 整除关系：DA={<x, y>|x, y∈A且x整除y}, 其中 AZ* , Z*是非零整数集 (6) 包含关系：R＝{<x, y>|x, y∈A且xy}, 其中A是集 合族。
离散数学
关系矩阵的实例
例9 设A={3, 5, 6, 9}, A上的二元关系
R={<x, y｜x＞y},
试求出关系矩阵。
[解] 关系的集合表示为:
R＝{9, 3, 9, 5, 9, 6, 6, 3, 6, 5, 5, 3}.
关系矩阵为: 0 1 MR= 1 1
关系的三种表示方法： 集合表达式 关系矩阵
关系图
关系矩阵和关系图可以表示有限集合上的关系。
离散数学
第二章 二元关系
2007年8月20日
关系矩阵
设给定集合A={a1,a2,…,an}，B={b1,b2,…,bm}，R为从A到B
的一个二元关系，构造一个n×m矩阵。用集合A的元素标注矩
阵的行，用集合B的元素标注矩阵的列，对于aiA和bjB，令
n2 n2
个. 不
每一个子集代表一个A上的二元关系，所以A上有 2 同的二元关系。 |Ai|=mi，则A1×A2×…×An上有 2 二元关系。
离散数学 第二章 二元关系 2007年8月20日
m1m2…mn
个不同的
常用的关系
定义 对任意集合A，定义 (1) 空关系 (2) 全域关系 EA={<x, y>|x∈A且y∈A}=A×A (3) 恒等关系 IA={<x, x>|x∈A} (4) 小于或等于关系：LA={<x, y>|x, y∈A且x≤y}, 其中 AR。 (5) 整除关系：DA={<x, y>|x, y∈A且x整除y}, 其中 AZ* , Z*是非零整数集 (6) 包含关系：R＝{<x, y>|x, y∈A且xy}, 其中A是集 合族。
离散数学 第8章 树(祝清顺版)88页PPT文档
e6
e5
e3
e10
e9 e11
e6
e7 e8
e10
e11
离散数学
第八章 树
2007年8月20日
生成树的存在条件
定理3 任何无向连通图G 至少存在一棵生成树.
[证] 若连通图G中无回路, 则G为自身的生成树. 若G中包含回路, 则随意地删除回路上的一条边, 而
vVdeg(vi) =2m =2(n1). 另一方面, 设T有x片树叶, 可得
2(n1)= vVdeg(vi) ≥x+2(nx) 由上式解出x≥2.
离散数学
第八章 树
2007年8月20日
例题
例2 设T为6条边的树, 其顶点度为1, 2, 3. 如果T恰有3个 度为2的顶点，那么T有多少片树叶？并画出满足要求的 非同构的无向树. [解] 设T有x片树叶, 于是结点总数为
本章将对树进行详细的讨论，主要包括：
树的基本性质和生成树，
根树、有向树中的n元树、有序树和搜索树等。
离散数学
第八章 树
2007年8月20日
Discrete Mathematics
科学出版社
第1节 树
主讲：祝清顺 教授
树的概念
定义1 连通而无简单回路的无向图称为无向树, 简称树, 常用T表示树. 在树中度数为1的结点称为树叶, 度数大于1的结点称为分支结点.
e1
e4 e2 e7 e8
e6
e5 e3Fra biblioteke10
e9 e11
e1 e4 e2 e5
e3
e9
生成树T1
离散数学
第八章 树
离散数学 第8章 树(祝清顺版)
说明
G的生成树一般不惟一. 余树不一定是树, 因为余树不一定连通, 也可能包 含回路.
离散数学
第八章
树
2007年8月20日
例题
例4 在下图中, 可以看到该图的绿线所示的一个生成树 T. 其中e1, e2, e3, e4, e5, e9都是T的树枝, e6, e7, e8, e10, e11都是T的弦.
树
2007年8月20日
例题
例4 利用破圈法求下图的生成树。
依次删去边e6,e7,e8,e10,e11, 所得到的生成树就是例
9.1.3中所给出一棵生成树T1.
e4 e2 e7 e8 e10 e9 e5 e6 e3 e11
e1 e1
e4
e2
e9
e5 e3
T的余树如右图所示, 余树是不连通的, 同时也包含回路.
e 4 e2 e7 e8 e10 e9 e5 e6 e3 e11
离散数学 第八章 树
e1
e7 e 8 e6 e10 e11
2007年8月20日
生成树的存在条件
定理3 任何无向连通图G 至少存在一棵生成树. [证] 若连通图G中无回路, 则G为自身的生成树. 若G中包含回路, 则随意地删除回路上的一条边, 而 不影响图的连通性. 若上仍有回路, 则再删除回路上的一条边, 直到无 回路为止, 最后得到的图是无回路、连通的且为G的生 成子图, 故为G的生成树.
离散数学 第八章 树 2007年8月20日
树简介
而系统地研究树，把树当成一个纯数学对象来研究的是法 国数学家约当(Jordan)。 1869年，约当(Jordan)作为一个纯数学对象独立地发现 了树，并给出了树的概念。 约当所研究的成果就是凯莱(Caylay Arthur)所要研究的，但他并不知道树
G的生成树一般不惟一. 余树不一定是树, 因为余树不一定连通, 也可能包 含回路.
离散数学
第八章
树
2007年8月20日
例题
例4 在下图中, 可以看到该图的绿线所示的一个生成树 T. 其中e1, e2, e3, e4, e5, e9都是T的树枝, e6, e7, e8, e10, e11都是T的弦.
树
2007年8月20日
例题
例4 利用破圈法求下图的生成树。
依次删去边e6,e7,e8,e10,e11, 所得到的生成树就是例
9.1.3中所给出一棵生成树T1.
e4 e2 e7 e8 e10 e9 e5 e6 e3 e11
e1 e1
e4
e2
e9
e5 e3
T的余树如右图所示, 余树是不连通的, 同时也包含回路.
e 4 e2 e7 e8 e10 e9 e5 e6 e3 e11
离散数学 第八章 树
e1
e7 e 8 e6 e10 e11
2007年8月20日
生成树的存在条件
定理3 任何无向连通图G 至少存在一棵生成树. [证] 若连通图G中无回路, 则G为自身的生成树. 若G中包含回路, 则随意地删除回路上的一条边, 而 不影响图的连通性. 若上仍有回路, 则再删除回路上的一条边, 直到无 回路为止, 最后得到的图是无回路、连通的且为G的生 成子图, 故为G的生成树.
离散数学 第八章 树 2007年8月20日
树简介
而系统地研究树，把树当成一个纯数学对象来研究的是法 国数学家约当(Jordan)。 1869年，约当(Jordan)作为一个纯数学对象独立地发现 了树，并给出了树的概念。 约当所研究的成果就是凯莱(Caylay Arthur)所要研究的，但他并不知道树
离散数学思维导图第一章
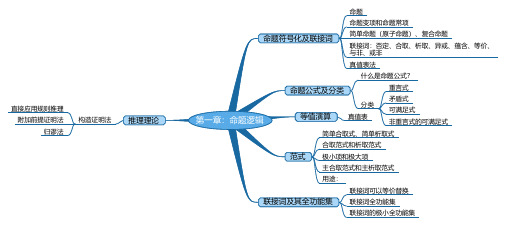
重言式
矛盾式可满足式非重言式的可满足式直接应用规则推理附加前提证明法
归谬法命题
命题变项和命题常项
简单命题（原子命题）、复合命题
联接词：否定、合取、析取、异或、蕴含、等价、与非、或非
什么是命题公式？
分类
真值表简单合取式、简单析取式
合取范式和析取范式
极小项和极大项
用途：
联接词可以等价替换
联接词全功能集
联接词的极小全功能集构造证明法真值表法
主合取范式和主析取范式
命题符号化及联接词命题公式及分类等值演算范式联接词及其全功能集推理理论第一章：命题逻辑。