2014北科大matlab数学实验第二次
MATLAB - 第二次试验结果

一
第
7、8 节课 张皓
指导老师
2.从键盘输入 a, b, c 的值,输出一元二次方程 ax 2 + bx + c = 0 的根。
%Ex02_02 function Ex02_02() disp(['一元二次方程是: a*x^2+b*x+c=0,请输入 各系数']); a=input('a='); b=input('b='); c=input('c='); roots([a b c])
price=input('请输入商品的价格='); zk=0.*(price<200)+... 0.03.*((price<500)&(price>=200))+... 0.05.*((price>=500)&(price<1000))+... 0.08.*((price>=1000)&(price<2500))+... 0.1.*((price>=2500)&(price<5000))+... 0.14.*(price>=5000); p=price*(1-zk); disp(['折扣=',num2str(zk*100),'%']) disp(['实际销售价钱=',num2str(p),'元'])
将它们的值互换后输出。 %Ex02_01 function exchange(x,y) %用来实现数据交换 disp(['交换前:x=',num2str(x),',y=',num2str(y)]); z=x; x=y; y=z; disp(['交换后:x=',num2str(x),',y=',num2str(y)]);
Matlab第二次实验报告
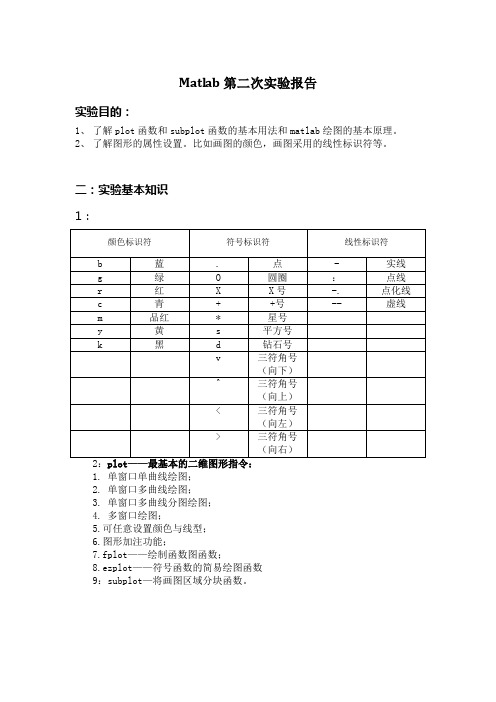
Matlab第二次实验报告实验目的:1、了解plot函数和subplot函数的基本用法和matlab绘图的基本原理。
2、了解图形的属性设置。
比如画图的颜色,画图采用的线性标识符等。
二:实验基本知识1:1. 单窗口单曲线绘图;2. 单窗口多曲线绘图;3. 单窗口多曲线分图绘图;4. 多窗口绘图;5.可任意设置颜色与线型;6.图形加注功能;7.fplot——绘制函数图函数;8.ezplot——符号函数的简易绘图函数9:subplot—将画图区域分块函数。
实验内容:将高数课本后的18个图画出上机练习程序第1——6图:clear,clca=input('ÇëÊäÈëaµÄÖµ£º')figure(1);x=-50:1:50;y=a.*x.^3;subplot(3,2,1);plot(x,y,'r');title('y=a*x^3');xlabel('X');ylabel('Y');x=0:1:50;y=sqrt(a.*x.^3);subplot(3,2,2);plot(x,y,x,-y,'r');title('y^2=a*x^3');xlabel('X');ylabel('Y');x=-3:0.1:3;y=exp(-x.^2);subplot(3,2,3);plot(x,y,'r');title('y=e^x^2');xlabel('X');ylabel('Y');x=-3:0.1:3;y=8*a^3./(x.^2+4*a^2);subplot(3,2,4);plot(x,y,'r');title('y=8*a^3./(x.^2+4*a^2)'); xlabel('X');ylabel('Y');x=0:0.01:5;y=sqrt(x.^3./(a*2.-x)); subplot(3,2,5);plot(x,y,x,-y,'r');title('y^2*(2a-x)=x^3'); xlabel('X');ylabel('Y');%t=-1:0.01:5;%x=3*a.*t./(1+t.^3);%y=3*a*t.^2./(1+t.^3);subplot(3,2,6);ezplot('x.^3+y.^3-3*3*x.*y'); %plot(x,y);title('x^3+y^3-3axy=0'); xlabel('X');ylabel('Y');输入a=3:显示结果第7——10图:clear,clca=input('ÇëÊäÈëaµÄÖµ£º')figure(1)t=0:0.1:2*pi;x=a*cos(t).^3;y=a*sin(t).^3;subplot(2,2,1);plot(x,y,'b')title('x^1.5+y^1.5=a^1.5'); xlabel('X');ylabel('Y');t=-2*pi:0.1:2*pi;x=a.*(t-sin(t));y=a.*(1-cos(t));subplot(2,2,2);plot(x,y,'b')title('°ÚÏß');xlabel('X');ylabel('Y');t=0:0.01:2*pi;p=a.*(1-cos(t));subplot(2,2,3);plot(p.*cos(t),p.*sin(t),'b'); title('p=a(1-cos£¨t£©)'); xlabel('X');ylabel('Y');t=0:0.01:2*pi;p=a.*t;subplot(2,2,4);plot(p.*cos(t),p.*sin(t),'b'); title('p=at');xlabel('X');ylabel('Y');输入a=1,第11题图:clear,clca=input('ÇëÊäÈëaµÄÖµ£º') figure(1);t=-2*pi:pi/100:2*pi;p=exp(a.*t);plot(p.*cos(t),p.*sin(t)); title('p=e^at');xlabel('X');ylabel('Y');输入a=0.1,显示结果:clear,clca=input('ÇëÊäÈëaµÄÖµ£º')figure(1)t=0.2*pi:pi/100:100*pi;p=a./t;plot(p.*cos(t),p.*sin(t));title('p=at');xlabel('X');ylabel('Y');输入a=1,显示结果:第13——14题图:clear,clca=input('ÇëÊäÈëaµÄÖµ£º');figure(1);t=0:pi/100:2*pi;p=(a^2.*sin(2*t)).^0.5;subplot(1,2,1);plot(p.*cos(t),p.*sin(t),-p.*cos(t),-p.*sin(t),'g'); title('p^2=a^2*sin(2t)');xlabel('X');p=(a^2.*cos(2*t)).^0.5;subplot(1,2,2);plot(p.*cos(t),p.*sin(t),-p.*cos(t),-p.*sin(t),'g'); title('p^2=a^2*cos(2t)');xlabel('X');ylabel('Y');输入a=1,显示结果:第15-16题图:clear;clc;a=input('ÇëÊäÈëa:');figure(1)t=0:pi/200:pi;p=a.*cos(3*t);subplot(1,2,1);plot(p.*cos(t),p.*sin(t),'r--');title('p=a*cos(3t)');xlabel('X');p=a.*sin(3*t);subplot(1,2,2);plot(p.*cos(t),p.*sin(t),'r--'); title('p=a*sin(3t)');xlabel('X');ylabel('Y');输入a=1,显示结果:第17——18题图:clear;clc;a=input('ÇëÊäÈëa:');figure(1);t=-pi:pi/200:pi;subplot(1,2,1);p=a.*sin(2*t);plot(p.*cos(t),p.*sin(t),'k-.'); title('p=a*sin(2t)');xlabel('X');ylabel('Y');p=a.*cos(2*t);subplot(1,2,2);plot(p.*cos(t),p.*sin(t),'k-.');title('p=a*cos(2t)');xlabel('X');ylabel('Y');输入a=1,显示结果:实验心得:这次实验主要是学习matlab软件的二维绘图功能:matlab软件还有丰富的图形修饰功能,如改变线条的形式和颜色;除此之外其还可以以多种形式如在一个图形中显示多个函数图形,一个figure中显示多个坐标系,还有一个程序中就可以用多个figure一起来表示不同的函数……在画图过程中你可能因为角度的区间取值不一样,画出来的图形可能跟书本上给出的图形有很大的差异,但没关系,只要你思路是对的,区间可以自己慢慢改动知道跟书本上给出的图形想接近。
matlab实验二答案

实验二 MATLAB环境的熟悉与基本运算(二)一、实验目的1.熟悉MATLAB 开发环境2.掌握矩阵、变量、表达式的各种基本运算二、实验内容1.设两个复数a=1+2i,b=3-4i,计算a+b,a-b,a×b,a/b。
程序:clca=1+2i,b=3-4i,x1=a+b,x2=a-b,x3=a*b,x4=a/b2.已知矩阵112A=134245⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦,1518B=20362545⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦,求A\B。
程序clca=[1 1 2;1 3 4;2 4 5] b=[15 18;20 36;25 45] x=a\b3.已知矩阵A为四阶魔方矩阵,矩阵13572468B=35794688⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦,求A+B,A-B和A*B。
程序:clca=magic(4)b=[1 3 5 7;2 4 6 8;3 5 7 9;4 6 8 8] x1=a+bx2=a-bx3=a*b4.试用简单的语句输入下面的矩阵(至少用两种方法):112233A 00A=0A 00A ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦,其中11-210A =0-2100-2⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦,22-310A =0-3100-3⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦,33-410A =0-4100-4⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦注:函数diag(V ,K )用来建立一个对角矩阵,其中V 为某个向量,K 为向量V 偏离主对角线的列数,K 为零时表示V 为主对角线,K 大于零的数时表示V 在主对角线以上,K 为小于零的数时表示V 在主对角线以下。
方法一:程序:clcA11=[-2 1 0;0 -2 1;0 0 -2] A22=[-3 1 0;0 -3 1;0 0 -3]A33=[-4 1 0;0 -4 1;0 0 -4]b=zeros(3)V=[A11 b b;b A22 b;b b A33]方法二:程序:clcA11=diag([-2 -2 -2],0)+diag([1 1],1)A22=diag([-3 -3 -3],0)+diag([1 1],1)A33=diag([-4 -4 -4],0)+diag([1 1],1)b=zeros(3)A=[A11 b b;b A22 b;b b A33]5. 用rand函数生成一个6阶的方阵A,(1)查询方阵A 第2 行、第3 列的元素,(2)查询方阵A 第2 行的所有元素,(3)查询方阵A 第6 列的所有元素,(4)给方阵A 第3 行、第2 列的元素赋值为5,(5)给方阵A 第3 行的所有元素赋值为4,(6)给方阵A 第1列的所有元素赋值为1。
北科大matlab数学实验报告第二次

《数学实验》报告实验名称 MATLAB绘图学院材料科学与工程学院专业班级材料0801 姓名 xxxxxxx 学号 xxxxxxxxx2011年10月一、【实验目的】学会用MATLAB绘制二维曲线、三维曲线、三维曲面,掌握gtext, legend, title, xlabel, ylabel等指令用法。
二、【实验任务】第四章3、5、9题。
三、【实验程序】1.x1=-pi:pi/100:pi;y1=x1.*cos(x1);x2=pi:pi/100:4*pi;y2=x2.*tan(1./x2).*sin(x2.^3);x3=1:0.1:8;y3=exp(1./x3).*sin(x3);subplot(131),plot(x1,y1,'rp'),grid onaxis tighttitle('y1=x1cosx1')xlabel('x轴'),ylabel('y轴')gtext('y1=x1cosx1')legend('y1=x1cosx1')subplot(132),plot(x2,y2,'c-'),grid onaxis tighttitle('y2=x2tan(1/x2)sin(x2^3)')xlabel('x轴'),ylabel('y轴')gtext('y2=x2tan(1/x2)sin(x2^3)')legend('y2=x2tan(1/x2)sin(x2^3)')subplot(133);plot(x3,y3,'mx'),grid onaxis tighttitle('y3=e^(1/x3)sin(x3)')xlabel('x轴'),ylabel('y轴')gtext('y3=e^(1/x3)*sin(x3)')legend('y3=e^(1/x3)sin(x3)')2. t=0:pi/10:20*pi;x=t.*cos(pi/6.*t);uy=t.*sin(pi/6.*t);z=2*t;plot3(x,y,z),grid onxlabel('x轴 x=tcos(pi/6t)')ylabel('y轴 y=tsin(pi/6t)')zlabel('z轴 z=2t')title('圆锥螺线(0≤t≤20pi)')legend('圆锥螺线')3. %三维曲面t=-2:0.01:2;[x,y]=meshgrid(t);z1=5-x.^2-y.^2+eps;subplot(131),mesh(x,y,z1),title('三维曲面')%平面subplot(1,3,2)z2=3*ones(size(x))mesh(x,y,z2)title('平面')%交线r0=abs(z1-z2)<=1;zz=r0.*z2;yy=r0.*y;xx=r0.*x;subplot(1,3,3),plot3(xx(r0~=0),yy(r0~=0),zz(r0~=0),'m-')title('交线')四、【实验结果】1.2.3.五、【实验总结】这次作业明显比第一次轻松了许多,在上课认真听讲后,又研读了书上的讲解和例题,起初是模仿,后来自己就能完全理解并做出题目来。
MATLAB第二次上机实验报告

电子科技大学电子工程学院标准实验报告(实验)课程名称MATLAB与数值分析学生姓名:学号:指导教师:一、实验名称实验二 线性方程组求解和函数的数值逼近二、实验目的通过上机实验,使学生对病态问题、线性方程组求解和函数的数值逼近方法有一个初步的理解。
实验涉及的核心知识点:病态方程求解、矩阵分解和方程组求解、Lagrange 插值。
实验重点与难点:算法设计和MATLAB 编程三、实验内容1. 对高阶多项式()()()()()2011220k p x x x x x k ==---=-∏编程求下面方程的解()190p x x ε+=并绘图演示方程的解与扰动量ε的关系。
2. 对220n =,生成对应的Hilbert 矩阵,计算矩阵的条件数;通过先确定解获得常向量b 的方法,确定方程组()n H x b =最后,用矩阵分解方法求解方程组,并分析计算结果。
3. 对函数()21125f x x =+ []1,1x ∈-的Chebyshev 点()()21cos 21k k x n π⎛⎫-= ⎪ ⎪+⎝⎭,1,2,,1k n =+编程进行Lagrange 插值,并分析插值结果。
四、实验数据及结果分析1. 对高阶多项式()()()()()2011220k p x x x x x k ==---=-∏编程求下面方程的解()190p x x ε+=并绘图演示方程的解与扰动量ε的关系。
p=[1,-1]; for i=2:20 n=[1,-i];p=conv(p,n); % 求多项式乘积 endm=zeros(1,21); % m 的最高次幂为20,有21项 hold on x=1:20;d=[-1,0,0.1,0.5,1]; for i=1:5delt=d(i); m(2)=delt;y=(roots(p+m))'; % 求多项式的根 plot(x,y,'-o','color',[i/5,i/20,i/10]); endtitle('方程p(x)=0的解与扰动量delt 的关系')legend('delt=-1','delt=0','delt=0.1','delt=0.5','delt=1')24681012141618200102030405060方程p(x)=0的解与扰动量delt 的关系delt=-1delt=0delt=0.1delt=0.5delt=12.对220n =,生成对应的Hilbert 矩阵,计算矩阵的条件数;通过先确定解获得常向量b 的方法,确定方程组()n H x b =最后,用矩阵分解方法求解方程组,并分析计算结果。
(matlab)数学实验报告二
相应函数值为y0,y1,…,yn(yi=f(xi),i=0,1,…,n)
曲线y= f(x)上相应的点为P0,P1,…,Pn(Pi=(xi,yi),i=0,1,…,n)
将曲线的每一段弧P(i-1)Pi用过点P(i-1),Pi的弦P(i-1)Pi(线性函数)来代替,这使得
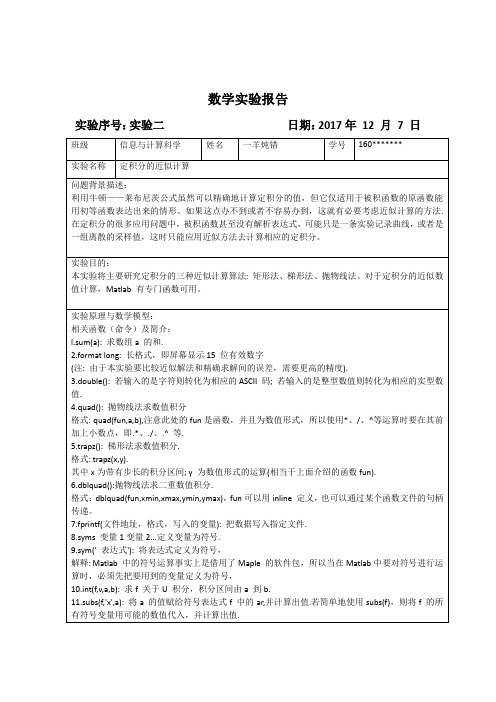
数学实验报告
实验序号:实验二日期:2017年12月7日
班级
信息与计算科学
姓名
一羊炖错
学号
160*******
实验名称
定积分的近似计算
问题背景描述:
利用牛顿——莱布尼茨公式虽然可以精确地计算定积分的值,但它仅适用于被积函数的原函数能用初等函数表达出来的情形。如果这点办不到或者不容易办到,这就有必要考虑近似计算的方法.在定积分的很多应用问题中,被积函数甚至没有解析表达式,可能只是一条实验记录曲线,或者是一组离散的采样值,这时只能应用近似方法去计算相应的定积分。
实验目的:
本实验将主要研究定积分的三种近似计算算法:矩形法、梯形法、抛物线法。对于定积分的近似数值计算,Matlab有专门函数可用。
实验原理与数学模型:
相关函数(命令)及简介:
l.sum(a):求数组a的和.
2.format long:长格式,即屏幕显示15位有效数字
(注:由于本实验要比较近似解法和精确求解间的误差,需要更高的精度).
end
inum5=inum5*h;
fprintf('积分为%g\n',inum5);
运算结果:积分为-1.33333
2.分别用梯形法与抛物线法,计算 ,将积分区间[1,2]作120等分.并尝试直接使用函数trapz()、quad()进行计算求解
matlab实验二及其答案
2.第 n 个 Fibonacci 定义如下:f(1)=1,f(2)=2,f(3)= f(1)+ f(2) ,…,f(n)= f (n-2)+ f(n-1) 。 编写程序,根据用户输入任何大于 2 的整数 n,计算出第 n 个 Fibonacci 数。 编写程序为: a(1)=1; a(2)=2; n=input('n='); k=2; while a(k)<=n a(k+1)=a(k)+a(k-1); k=k+1; end num=a(k) Fibonacci=[1:length(a);a]' 程序运行结果为: n=5 num = 8 Fibonacci = 1 1 2 2 3 3 4 5 5 8 3.编写程序能够根据用户输入的 x,y 值,给出下面表达式对应的解,给定表达式为:
f = x+exp(y); fprintf('f(x,y) = %f\n',f); else f = x*exp(x)-y*exp(x*y); fprintf('f(x,y) = %f\n',f); end end 程序运行结果为:
Please enter x:-3 Please enter y:-4 f(x,y) = 1.000000 Please enter x:-pi/2 Please enter y:2 f(x,y) = 1.000000 Please enter x:2 Please enter y:-1 f(x,y) = 2.367879
matlab实验2下载-支持高清免费浏览-max文档
plot(real(y),imag(y))。
example
y=[1,2,4,8,16,32,64,128]; plot(y)
example
x=[1:1:100]; y=[2:2:200]; z=x+y.*i; plot(z)
plot —— 最基本的二维图形指令
◆plot(x,y) —— ◆ 基本格式,以y(x)的函数关系作出直角坐标 图。 ◆x,y均可为向量和矩阵,其中有3种组合用于绘 制连线图。 ◆x,y均为n维向量时,绘制向量y对向量x的图形, 即以x为横坐标,y为纵坐标。 ◆x,y均为m×n的矩阵,将绘制n条不同颜色的连 线。绘制规则为:以x矩阵的第i列分量作为横坐标, 矩阵y的第i列分量作为纵坐标,绘得第i条连线。
纵向排列
备注说明:
subplot(m,n,p) 将一图形窗口分成m × n 个小窗口,在第p个小窗口中创建一坐标轴, 则新的坐标轴成为当前坐标轴。若p为一向 量,则创建一坐标轴,包含所有罗列在p中 的小窗口。用户可以通过参数p分别对各子 绘图区域进行操作,子绘图区域的编号从左 至右编号。
备注说明:
在已存的图中添加新的曲线,要求几个图形 在同一个图形窗口,但新的曲线不在同一个 坐标系中绘制,需要用到hold和subplot函 数。 hold on 启动图形保持功能,此后绘制的图 形都将添加到当前的图形窗口中,并自动调 整坐标轴范围。 hold off 关闭图形保持功能。 hold 在hold on和hold off之间切换。
MTALAB 实验二
实验内容:
二维图绘制 子图绘制 三维图绘制 Simulink初步
plot —— 最基本的二维图形指令
北京科技大学《matlab和数学实验》 第二次课
数学实验
例1 画出函数y = sin x2 在-5 x 5 的图形。
解: Matlab 命令: x=-5:0.1:5;↙ y=sin(x.^2); ↙ plot(x,y),grid on
X=a:h:b; 步长h可以任意选取, 步长越小,曲线越光滑。
grid on作用是:在图形中标出网格线
例 x=[ 3 4 7]; y=[4 5 6 5 4795 1 4 2 5]; plot (x,y)
6
数学实验
• 思考: 1、当x为n维向量,y为m x n 矩阵时, plot(x,y)怎么画? 2、当x为n维向量,y为m x w 矩阵时, plot(x,y)怎么画? 3、当x为n维向量,y为n x n 矩阵时, plot(x,y)怎么画?
数学实验
• Mesh命令介绍
– 利用函数meshgrid生成格点矩阵后,然后 求出各格点对应的函数值,就可以利用三维 网格命令mesh画出空间曲面。
– 函数mesh用来生成函数的网格曲面,即各 网格线段组成的曲面。
25
例:x=[1,2,3] y=[1,2,3,4] [X,Y]=meshgrid(x,y)
19
数学实验
• 例7 在同一坐标系中画出两个函数y = cos 2x ,y = x的图形, 自变量范围为:-2 x 2,函数y = cos 2x为红色实线, 函数y = x 为蓝色点划线。并加注标题,坐标轴。 解: Matlab命令为 clf x=-2:.1:2; y1=cos(2*x);y2=x; subplot(1,2,1) plot(x,y1,'r-',x,y2,'b-.'),grid on title('曲线y1=cos(2x)与y2=x') xlabel('x轴'),ylabel('y轴') gtext('y1=cos(2x)'),gtext('y2=x') legend('y1=cos(2x)','y2=x') subplot(1,2,2) plot (x,y1,x,y2)
Matlab数学实验报告二
数学软件课程设计题目线性方程组求解班级数学081姓名曹曼伦实验目的:用Matlab语言实现Gauss算法和cholesky算法(chol)以及LU分解(lu),求解一般线性方程组。
用Matlab语言实现Jacobi迭代算法、Gauss-Seidel迭代算法和逐次超松弛迭代法,求解一般的线性代数方程组问题。
实验内容:一.直接法(1)Gauss消元法:function x=DelGauss(a,b)% Gauss消去法[n,m]=size(a);nb=length(b);det=1;%存储行列式值x=zeros(n,1);for k=1:n-1for i=k+1:nif a(k,k)==0returnendm=a(i,k)/a(k,k);for j=k+1:na(i,j)=a(i,j)-m*a(k,j);endb(i)=b(i)-m*b(k);enddet=det*a(k,k);enddet=det*a(n,n);for k=n:-1:1 %回代for j=k+1:nb(k)=b(k)-a(k,j)*x(j);endx(k)=b(k)/a(k,k);endExample:>> A=[1.0170 -0.0092 0.0095;-0.0092 0.9903 0.0136;0.0095 0.0136 0.9898]; >> b=[1 0 1]';>> x=DelGauss(A,b)x =0.9739-0.00471.0010(2)对称正定矩阵之Cholesky分解法:function L=Cholesky(A)%对对称正定矩阵A进行Cholesky分解n=length(A);L=zeros(n);for k=1:ndelta=A(k,k);for j=1:k-1delta=delta-L(k,j)^2;endif delta<1e-10return;endL(k,k)=sqrt(delta);for i=k+1:nL(i,k)=A(i,k);for j=1:k-1L(i,k)=L(i,k)-L(i,j)*L(k,j);endL(i,k)=L(i,k)/L(k,k);endendfunction x=Chol_Solve(A,b)%利用对称正定矩阵之Cholesky分解求解线性方程组Ax=b n=length(b);l=Cholesky(A);x=ones(1,n);y=ones(1,n);for i=1:nz=0;for k=1:i-1z=z+l(i,k)*y(k);endy(i)=(b(i)-z)/l(i,i);endfor i=n:-1:1z=0;for k=i+1:nz=z+l(k,i)*x(k);endx(i)=(y(i)-z)/l(i,i);endExample:>> A=[1.0170 -0.0092 0.0095;-0.0092 0.9903 0.0136;0.0095 0.0136 0.9898];>> b=[1 0 1]';>> x=Chol_Solve(A,b)x =0.9739 -0.0047 1.0010(3)LU分解法:function [l,u]=lu(a)%LU分解n=length(a);l=eye(n);u=zeros(n);for i=1:nu(1,i)=a(1,i);endfor i=2:nl(i,1)=a(i,1)/u(1,1);endfor r=2:n%%%%for i=r:nuu=0;for k=1:r-1uu=uu+l(r,k)*u(k,i);endu(r,i)=a(r,i)-uu;end%%%%for i=r+1:nll=0;for k=1:r-1ll=ll+l(i,k)*u(k,r);endl(i,r)=(a(i,r)-ll)/u(r,r);end%%%%Endfunction x=lusolv(a,b)%LU分解求解线性方程组aX=b if length(a)~=length(b)error('Error in inputing!')return;endn=length(a);[l,u]=lu(a);y(1)=b(1);for i=2:nz=0;for k=1:i-1z=z+l(i,k)*y(k);endy(i)=b(i)-z;endx(n)=y(n)/u(n,n);for i=n-1:-1:1z=0;for k=i+1:nz=z+u(i,k)*x(k);endx(i)=(y(i)-z)/u(i,i);endExample:>> a=[1.0170 -0.0092 0.0095;-0.0092 0.9903 0.0136;0.0095 0.0136 0.9898]; >> b=[1 0 1]';>> x=Chol_Solve(a,b)x =0.9739 -0.0047 1.0010二.迭代法(1)Jacobi迭代法:function [x,n]=jacobi(A,b,x0,eps,varargin)if nargin==3eps= 1.0e-6;M = 200;elseif nargin<3errorreturnelseif nargin ==5M = varargin{1};D=diag(diag(A)); %求A的对角矩阵L=-tril(A,-1); %求A的下三角阵U=-triu(A,1); %求A的上三角阵B=D\(L+U);f=D\b;x=B*x0+f;n=1; %迭代次数while norm(x-x0)>=epsx0=x;x=B*x0+f;n=n+1;if(n>=M)disp('Warning: 迭代次数太多,可能不收敛!');return;endendExample:>> x0=[0;0;0]x0 =>> [x,n]=Jacobi(A,b,x0)x =0.9739-0.00471.0010n =5(2)Gauss-Seidel迭代法:function [x,n]=gauseidel(A,b,x0,eps,M) if nargin==3eps= 1.0e-6;M = 200;elseif nargin == 4M = 200;elseif nargin<3errorreturn;endD=diag(diag(A)); %求A的对角矩阵L=-tril(A,-1); %求A的下三角阵U=-triu(A,1); %求A的上三角阵f=(D-L)\b;x=G*x0+f;n=1; %迭代次数while norm(x-x0)>=epsx0=x;x=G*x0+f;n=n+1;if(n>=M)disp('Warning: 迭代次数太多,可能不收敛!');return;endendExample:>> x0=[0;0;0]x0 =>> [x,n]=gauseidel(A,b,x0)x =-0.00471.0010n =4(3)对称逐次超松驰迭代法:function [x,n]=SSOR(A,b,x0,w,eps,M) if nargin==4eps= 1.0e-6;M = 200;elseif nargin<4errorreturnelseif nargin ==5M = 200;endif(w<=0 || w>=2)error;return;endD=diag(diag(A)); %求A的对角矩阵L=-tril(A,-1); %求A的下三角阵U=-triu(A,1); %求A的上三角阵B1=inv(D-L*w)*((1-w)*D+w*U);B2=inv(D-U*w)*((1-w)*D+w*L);f1=w*inv((D-L*w))*b;f2=w*inv((D-U*w))*b;x12=B1*x0+f1;x =B2*x12+f2;n=1; %迭代次数while norm(x-x0)>=epsx0=x;x12=B1*x0+f1;x =B2*x12+f2;n=n+1;if(n>=M)disp('Warning: 迭代次数太多,可能不收敛!');return;endendExample:>> [x,n]=SSOR(A,b,x0,1)x =0.9739-0.00471.0010n =3实验结果:一.直接法(1)Gauss消元法:>> A=[1.0170 -0.0092 0.0095;-0.0092 0.9903 0.0136;0.0095 0.0136 0.9898]; >> b=[1 0 1]';>> x=DelGauss(A,b)x =0.9739-0.00471.0010(2)对称正定矩阵之Cholesky分解法:>> A=[1.0170 -0.0092 0.0095;-0.0092 0.9903 0.0136;0.0095 0.0136 0.9898];>> b=[1 0 1]';>> x=Chol_Solve(A,b)x =0.9739 -0.0047 1.0010(3)LU分解法:>> a=[1.0170 -0.0092 0.0095;-0.0092 0.9903 0.0136;0.0095 0.0136 0.9898]; >> b=[1 0 1]';>> x=Chol_Solve(a,b)x =0.9739 -0.0047 1.0010二.迭代法(1)Jacobi迭代法:>> [x,n]=Jacobi(A,b,x0)x =0.9739-0.00471.0010n =5(2)Gauss-Seidel迭代法:>> [x,n]=gauseidel(A,b,x0)x =0.9739-0.00471.0010n =4(3)对称逐次超松驰迭代法:>> [x,n]=SSOR(A,b,x0,1)x =0.9739-0.00471.0010n =3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《数学实验》报告
实验名称第二次数学实验
学院材料科学与工程学院专业班级材料1101
姓名郝佳
学号 41130026
2014年5月
一、 【实验目的】
1. 掌握MATLAB 的基本语法和函数.
2. 掌握MATLAB 中函数plot 绘制二维图形。
二、 【实验任务】
1. 完成第三章课后练习P34第3题;
2. 完成第四章课后练习P79第1、3题。
三、 【实验程序】
1. 编写函数,计算1!+2!+ (50)
function y=function1 n=1; i=1; y=0;
while i<=50 n=n*I; y=y+n; i=i+1; end
2. 绘制])4,0[)(3sin(y 3
π∈=x x e x
的图像,要求用蓝色的星号画图,并且画出其包络线
3
y x e ±=的图像,用红色的点划线画图。
x=0:pi/50:4*pi;
y=exp(x/3).*sin(3.*x); plot(x,y,'b*') hold on
y2=exp(x/3); plot(x,y2,'r-.') y3=-exp(x/3); plot(x,y3,'r-.') grid on
3. 在同一个图形窗口画三个子图,要求使用指令gtext 、axis 、legend 、title 、 xlabel 、
ylabel :
[]
8,1,sin )3()
4,(,sin 1
tan )2(),(,cos )1(1
3∈=∈=-∈=x x e y x x x x y x x x y x ππππ
x1=-pi:pi/50:pi; x2=pi:pi/50:4*pi; x3=1:pi/50:8;
y1=x1.*cos(x1);
y2=x2.*tan(1./x2).*sin(x2.*x2.*x2);
y3=exp(1./x3).*sin(x3);
plot(x1,y1,x2,y2,x3,y3),grid on
title('曲线y1=xcos(x)与y2=xtan(1/x)sin(x^3)与y3=exp(1/x)sin(x)')
xlabel('x轴'),ylabel('y轴')
gtext('y1=xcos(x)'),gtext('y2=xtan(1/x)sin(x^3)'),gtext('y3=exp(1/x)sin(x)'),
legend('y1=xcosx','y2=xtan(1/x)sin(x^3)','y3=exp(1/x)sinx')
四、【实验结果】
1.
2.
3.
五、【实验总结】
数学实验让我们初步掌握了MATLAB的基本语法和函数,以及如何在MATLAB中利用函数plot绘制二维图形,完成了MATLAB的基本语法和函数的任务和函数plot绘制二维图形的任务。
MATLAB是非常实用的数学工具。
