北京八中20092010学年度第二学期开学测试_2
北京市东城区09—10下学期初二语文期末考试试卷
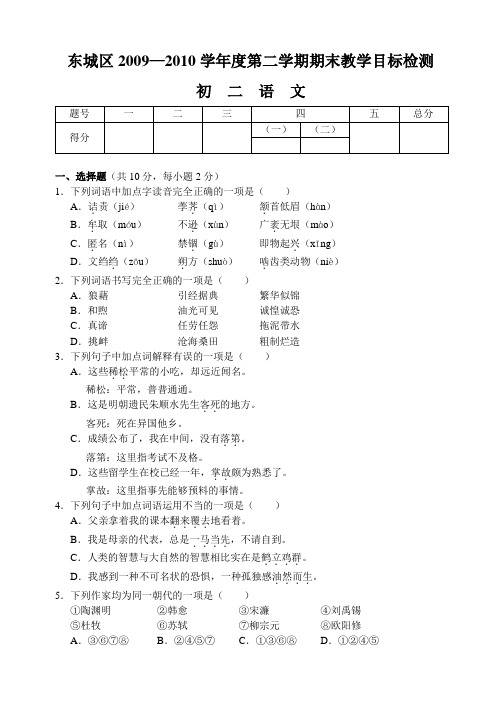
东城区2009—2010学年度第二学期期末教学目标检测初二语文一、选择题(共10分,每小题2分)1.下列词语中加点字读音完全正确的一项是()A.诘.责(jié)荸荠.(qì)颔.首低眉(hàn)B.牟.取(móu)不逊.(xùn)广袤.无垠(mào)C.匿.名(nì)禁锢.(gù)即物起兴.(xīng)D.文绉绉.(zōu)朔.方(shuò)啮.齿类动物(niè)2.下列词语书写完全正确的一项是()A.狼藉引经据典繁华似锦B.和煦油光可见诚惶诚恐C.真谛任劳任怨拖泥带水D.挑衅沧海桑田粗制烂造3.下列句子中加点词解释有误的一项是()A.这些稀松..平常的小吃,却远近闻名。
稀松:平常,普普通通。
B.这是明朝遗民朱顺水先生客死..的地方。
客死:死在异国他乡。
C.成绩公布了,我在中间,没有落第..。
落第:这里指考试不及格。
D.这些留学生在校已经一年,掌故..颇为熟悉了。
掌故:这里指事先能够预料的事情。
4.下列句子中加点词语运用不当的一项是()A.父亲拿着我的课本翻来覆去....地看着。
B.我是母亲的代表,总是一马当先....,不请自到。
C.人类的智慧与大自然的智慧相比实在是鹤立鸡群....。
D.我感到一种不可名状的恐惧,一种孤独感油然而生....。
5.下列作家均为同一朝代的一项是()①陶渊明②韩愈③宋濂④刘禹锡⑤杜牧⑥苏轼⑦柳宗元⑧欧阳修A.③⑥⑦⑧B.②④⑤⑦C.①③⑥⑧D.①②④⑤二、简答题(16分)6.默写(8分)(1)至若春和景明,________,________,一碧万顷。
(范仲淹《岳阳楼记》)(2)作亭者谁?________。
名之者谁?________。
(欧阳修《醉翁亭记》)(3)沉舟侧畔千帆过,________________。
________________,暂凭杯酒长精神。
(刘禹锡《酬乐天扬州初逢席上见赠》)(4)《水调歌头》“此事古难全”中的“此事”是指:___________,___________。
北京市八一中学2009-2010学年高二第二学期期中试卷物理答案

高二物理期中参考答案2010.04一.单项选择题:二、不定项选择题:三、填空题:16.2.1 17. 小于;大于 18. 1/(2πLC );t =πLC19.102,610107⨯ 四、实验题:20.(1)单摆的摆长L =_ L 0+d/2__;(2)单摆的周期T =t/n ; (3)当地的重力加速度g =4π2n 2(L 0+d/2)/t 2。
(4) ( B ) 21.图中A 位置的游标卡尺读数为11.1mm ,B 位置的游标卡尺读 数为15.6mm ,单色光的波长为6.4×10-7m 。
五、计算题:22.解:由s = c Δt =1.2×108m=1.2×105km 。
这是电磁波往返的路程,所以目标到雷达的距离为60000km 。
由c = f λ可得λ= 0.1m23题(1)因21()t t t T ∆=-<,所以波传播的距离小于一个波长,可以直接由图读出。
因为波向右传播,则在0.005s 内传播了2m ,故波速为:2/400/0.005s v m s m st ∆===∆ 因21()t t t T ∆=-<,所以波传播的距离小于一个波长,可以直接由图读出。
因为波向左传播,则在0.005s 内传播了6m ,故波速为: 6/1200/0.005s v m s m st ∆===∆ (2)因21()t t t T ∆=->,所以传播的距离大于一个波长,在t ∆内传播的距离为60000.00530s v t m m ∆=∆=⨯= 即 33034s m λλ∆==+因此,可得波的传播方向沿x 轴的负方向。
24题。
(1)只挂A 球时弹簧伸长量由F kx =得1A m gx k=·········① 挂A 、B 两球时有()A B m m kx += 得()A B m m g k x+=········②由①②式可得110015 2.5100500A AB m x x cm cm m m ==⨯=++所以,A 的振幅115 2.512.5A x x cm cm cm =-=-= (2)剪断细绳瞬间,A 受到最大的弹力,合力最大,加速度最大,则 m a x m a x )()A B A B A F m m g m g m g m a =+-==合( 得 最大加速度为:22max 50010/50/100B A m g a m s m s m ==⨯= 25. 光线1能在圆锥的侧面B 点发生全反射。
北京市西城区2008~2009学年度第二学期学业测试

北京市西城区2008~2009学年度第二学期学业测试高一数学试卷 2009.6本试卷满分:150分考试时间:120分钟参考公式:圆锥的侧面积公式S 圆锥侧=πRl ,其中R 是圆锥的底面半径,l 是圆锥的母线长.球的表面积公式S 球=4πR 2,其中R 是球半径.锥体的体积公式V 锥体=31Sh ,其中S 是锥体的底面积,h 是锥体的高. 一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.1.点M (-2,6)关于坐标原点的中心对称点为( ) (A )M ′(-6,2) (B )M ′(2,-6) (C )M ′(-1,3) (D )M ′(3,-1) 2.下列直线中,与直线3x +y -2=0垂直的是( ) (A )3x -y -2=0 (B )3x +y +2=0 (C )x -3y -2=0 (D )x +3y +2=0 3.在空间直角坐标系中,两点A (1,0,-2)和B (-2,4,3)的距离是( ) (A )5(B )25(C )3(D )234.已知球的大圆周长是2π,那么球的表面积是( ) (A )π (B )2π (C )3π (D )4π5.若过点A (-2,m )和B (4,0)的直线与直线2x +y -1=0平行,则m 的值为( ) (A )12 (B )-12 (C )3 (D )-3 6.圆x 2+y 2=1和圆x 2+y 2-6y +5=0的位置关系是( ) (A )内含 (B )内切 (C )外切 (D )外离 7.将直线x y 3=绕原点逆时针旋转60°,所得到的直线为( )(A )x =0(B )y =0(C )x y 33-= (D )x y 3-=8.在空间,若a 、b 是不重合的直线,α、β是不重合的平面,则下列条件中可推出a ⊥b 的是( ) (A )a ∥α,b ∥α (B )a ⊥α,b ⊥α (C )a ⊂α,b ⊂β,α⊥β (D )α∥β,a ⊥α,b ⊂β9.如果圆(x -a )2+(y -b )2=1的圆心在第三象限,那么直线ax +by -1=0一定不经过...( ) (A )第一象限 (B )第二象限 (C )第三象限 (D )第四象限 10.已知某地球仪的半径是20cm ,那么该地球仪上北纬60°纬线的长度为( )(A )20πcm (B )16πcm (C )12πcm (D )10πcm 二、填空题:本大题共6小题,每小题4分,共24分.把答案填在题中横线上. 11.若直线l 通过点(1,0),且斜率是3,则直线l 的方程是______. 12.圆锥的底面半径是3,高是4,则圆锥的侧面积是______. 13.如果直线y =a 和圆x 2+y 2-2y =0相切,那么a 等于______.14.下图是一个几何体的三视图:根据图中数据,可得该几何体的体积是______;表面积是______. 15.如果圆(x -1)2+(y -b )2=2被x 轴截得的弦长是2,那么b =______.16.已知△ABC 是等腰直角三角形,AB =AC =a ,AD 是斜边BC 上的高,以AD 为折痕使∠BDC 成直角.在折起后形成的三棱锥A -BCD 中,有如下三个结论: ①直线AD ⊥平面BCD ; ②侧面ABC 是等边三角形;③三棱锥A -BCD 的体积是.2423a 其中正确结论的序号是______.(写出全部正确结论的序号)三、解答题:本大题共3小题,共36分.解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)如图,三棱锥P -ABC 的三个侧面均为边长是1的等边三角形,M ,N 分别为P A ,BC 的中点. (1)求MN 的长; (2)求证:P A ⊥BC ;(3)求三棱锥P -ABC 的表面积.18.(本小题满分12分)已知平面上三个定点A (-1,0),B (3,0),C (1,4). (1)求点B 到直线AC 的距离;(2)求经过A 、B 、C 三点的圆的方程.19.(本小题满分12分)如图,在斜三棱柱ABC -A 1B 1C 1中,AC =BC ,AC ⊥BC .侧面A 1ABB 1是边长为a 的菱形,且垂直于底面ABC ,∠A 1AB =60°,E ,F 分别是AB 1,BC 的中点.(1)求证:直线EF ∥平面A 1ACC 1;(2)在线段AB 上确定一点G ,使平面EFG ⊥平面ABC ,并给出证明; (3)记三棱锥A -BCE 的体积为V ,且]12,23[ V ,求a 的取值范围.B 卷[学期综合] 满分50分1.在△ABC 中,三个内角A ,B ,C 的对边分别为a ,b ,c .若a =1,b =2,3π2=C ,则边c 等于______. 2.如果a >b >0,c >0.设cb ca Nb a M ++==,那么M ______N (填“>”或“<”). 3.在等差数列{a n }中,a 2=2,a 4=6,若b n =a 2n ,则数列{b n }的前5项和等于______.4.等比数列{a n }的前n 项和是S n ,若8S 6=9S 3,则{a n }的公比为______.5.设k >0,则不等式组⎪⎩⎪⎨⎧≥+≤-≤0,0,2ky x y kx y ,所表示的平面区域面积的最小值是______.二、解答题:本大题共3小题,共30分.解答应写出文字说明、证明过程或演算步骤. 6.(本小题满分10分)在△ABC 中,三个内角A ,B ,C 的对边分别为a ,b ,c ,且⋅===53cos ,4π,2B C a (1)求sin A 的值;(2)求△ABC 的面积S .7.(本小题满分10分)设a >0,函数aa ax x x f 3)(2-++=的定义域是{x |-1≤x ≤1}. (1)当a =1时,解不等式f (x )<0;(2)若f (x )的最大值大于6,求a 的取值范围.8.(本小题满分10分)在数列{a n }中,a 1=0,a n +1=-a n +3n ,其中n =1,2,3,…. (1)求a 2,a 3的值;(2)求数列{a n }的通项公式; (3)求1+n na a 的最大值.测试卷参考答案北京市西城区2008~2009学年度第二学期学业测试高一数学试卷参考答案及评分标准A 卷[必修模块2]满分100分一、选择题:本大题共10小题,每小题4分,共40分1.B 2.C 3.B 4.D 5.A 6.C 7.D 8.D 9.A 10.A 二、填空题:本大题共6小题,每小题4分,共24分 11.3x -y -3=0 12.15π 13.0或2 14.16π;24π 15.±1 16.①、②、③注:13、15题每解各2分;14题每空2分;16题少填不给分. 三、解答题:本大题共3小题,共36分 17.(1)解:连接MB ,MC .因为 三棱锥P -ABC 的三个侧面均为边长是1的等边三角形, 所以 23==MC MB ,且底面△ABC 也是边长为1的等边三角形. 因为 N 为BC 的中点, 所以 MN ⊥BC . 在Rt △MNB 中,⋅=-=2222BN MB MN ………………4分 (2)证明:因为M 是P A 的中点, 所以 P A ⊥MB , 同理 P A ⊥MC . 因为MB ∩MC =M , 所以 P A ⊥平面MBC , 又因为 BC ⊂平面MBC ,所以 P A ⊥BC . ………………8分 (3)解:因为 侧面等边三角形APB 的面积为,4321=⋅=MB AP S且三棱锥P -ABC 的三个侧面和底面均为边长是1的等边三角形,所以 三棱锥P -ABC 的表面积为.34=S ……………12分18.(1)解:直线AC 的斜率是,2)1(104=---所以直线AC 的方程为y -0=2(x +1),即2x -y +2=0. ………………3分 所以点B 到直线AC 的距离为⋅=-++⨯558)1(2|232|22 ………………6分 (2)解:设所求圆的方程为x 2+y 2+Dx +Ey +F =0. 将A 、B 、C 三点的坐标代入圆的方程,得⎪⎩⎪⎨⎧=+++=++=+-.0417,039,01F E D F D F D 解得⎪⎩⎪⎨⎧-=-=-=.3,3,2F E D 于是所求圆的方程为x 2+y 2-2x -3y -3=0. ……………12分 19.(1)证明:连接A 1C ,A 1E .因为侧面A 1ABB 1是菱形,E 是AB 1的中点, 所以 E 也是A 1B 的中点, 又因为 F 是BC 的中点, 所以 EF ∥A 1C .因为A 1C ⊂平面A 1ACC 1,EF ⊄平面A 1ACC 1, 所以直线EF ∥平面A 1ACC 1. …………4分 (2)解:当31=GA BG 时,平面EFG ⊥平面ABC , 证明如下: ………………5分 连接EG ,FG .因为侧面A 1ABB 1是菱形,且∠A 1AB =60°, 所以 △A 1AB 是等边三角形. 因为 E 是A 1B 的中点,31=GA BG , 所以EG ⊥AB .因为 平面A 1ABB 1⊥平面ABC ,且平面A 1ABB 1∩平面ABC =AB ,所以EG ⊥平面ABC . 又因为EG ⊂平面EFG ,所以平面EFG ⊥平面ABC . ………………8分 (3)解:因为△A 1AB 是边长为a 的等边三角形, 所以,43a EG =所以348321.31a EG BC AC V V V ABC E BCE A =⋅⋅===--.根据12483233≤≤a ,解得,3432≤≤a 即]34,32[∈a . …………12分B 卷 [学期综合] 满分50分一、填空题:本大题共5小题,每小题4分,共20分.(一题两空的题目每空2分) 1.7 2.> 3.50 4.215.4 二、解答题:本大题共3小题,共30分. 6.(1)解:因为在△ABC 中,53cos =B , 所以 B 为锐角,且54cos 1sin 2=-=B B . ………………2分 所以⋅=-=-=1027sin 4π3cos cos 4π3sin )4π3sin(sin B B B A .………………5分(2)解:由正弦定理得,sin sin CcA a = 得⋅=710c . ………………8分 所以⋅=⋅=78sin 21B ac S . ………………10分7.(1)解:当a =1时,f (x )<0,即x 2+x -2<0,解得-2<x <1. ………………2分 因为-1≤x ≤1,所以 不等式f (x )<0的解集为{x |-1≤x <1}. ………………4分 (2)).11(34)2(3)(222≤≤--+-+=-++=x aa a ax aa ax xx f因为f (x )的图象是开口向上的抛物线,其对称轴方程是2ax -=, 注意到a >0,所以f (x )的最大值为aa f 321)1(-+=. ………………7分 依题意,6321>-+aa 整理得2a 2-5a -3>0. 解得a >3,或⋅-<21a (舍去) 所以a 的取值范围是(3,+∞). ……………10分 8.(1)解:由a 1=0,且a n +1=-a n +3n (n =1,2,3,…), 得a 2=-a 1+3=3,a 3=-a 2+32=6. ………………2分(2)解:将a n +1=-a n +3n 变形为),43(4311n n n n a a --=-++, ………………4分从而数列}43{nn a -是首项为43431-=-a ,公比为-1的等比数列,所以,)1(43431--⋅-=-n n n a 即).,3,2,1(43.)1(43 =-+=n a n n n . ………………6分 (3)解:①当n 是偶数时,334313333434343431111-+=-+=-+=++++n n n n n n n a a ,所以1+n n a a随n 的增大而减小,从而,当n 是偶数时,1+n n a a 的最大值是⋅=2132a a . ………………8分②当n 是奇数时,,334313333434343431111+-=+-=+-=++++n n n n n n na a所以1+n n a a随n 的增大而增大,且⋅<<+-=++21313343111n n naa综上,1+n n a a的最大值是⋅21………………10分。
2008-2009学年度九年级数学第二学期开学测试

四中2008-2009学年度第二学期初三数学开学测试测试试题一、选择题(本大题共8小题,每小题4分,共32分,在每小题给出的四个选项中,只有一项是符合题意的)1.在下列各图中,既是轴对称图形又是中心对称图形的是( ).2.有9X相同的卡片,上面写有汉字:“我、努、力、我、收、获、我、快、乐”,9X 卡片任意搅乱后,一个人随机抽取一X,卡片上写有汉字“我”的概率是( ).A. B. C. D.3.两个圆的半径分别是2cm和7cm,圆心距是5cm,则这两个圆的位置关系是( ).A.外离B.内切C.相交D.外切4.在Rt△ABC中,∠C=90°,,则等于( ).A. B. C. D.5.将二次函数的图象先向右平移2个单位,再向下平移3个单位,得到的函数图象的解析式是( ).A. B.C. D.6.在同一坐标系中,直线和抛物线的图象只可能是( ).7.如下图,量角器外沿上有A、B两点,它们的读数分别是70°、40°,则∠1的度数为( ).°°°°8.如右图,正方形ABCD的边长为10,四个等圆的圆心分别在正方形ABCD的顶点上.若圆的半径为x,且0<x ≤5,图中四个阴影部分面积的和为y,则能反映y与x 之间函数关系的大致图象是( ).二、填空题(本大题共4小题,每小题4分,共16分)9.据调查,市机动车拥有量2005年底达到了近260万辆,而截至2007年底,市机动车拥有量已达到了近314.6万辆,如果假设2005年至2007年市机动车拥有量每年的增长率相同,则此增长率为______________.10.已知关于的方程有两个实数根,则k的取值X围为______________.11.某个立体图形的三视图如下,则这个立体图形的表面积为______________平方厘米.12.如图,已知在⊙中,直径,正方形ABCD的四个顶点分别在半径OM、OP 以及⊙上,并且,则AB的长为______________.三、解答题(本题共25分,每小题5分)13.计算:.14.用配方法解方程:.15.如图,在⊙O中,弦MN=12,半径OA⊥MN,垂足为B,AB=3,求OA的长.16.已知:如图,若AD=3cm,AB=7cm,AC=cm,试证:∠ABC=∠ACD.17.如图,在中,,且点的坐标为(4,2).(1)画出绕点逆时针旋转后的;(2)求点旋转到点所经过的路线长.四、解答题(本题共47分)18.(本小题满分5分)彤彤和朵朵玩纸牌游戏.下图是同一副扑克中的4X扑克牌的正面,将它们正面朝下洗匀后放在桌上,彤彤先从中抽出一X,朵朵从剩余的3X牌中也抽出一X.彤彤说:若抽出的两X牌的数字都是偶数,你获胜;否则,我获胜.(1)请用树状图或列表法表示出两人抽牌可能出现的所有结果;(2)若按彤彤说的规则进行游戏,这个游戏公平吗?请说明理由.19.(本小题满分5分)如图,小明为了测量一铁塔的高度CD,他先在A处测得塔顶C 的仰角为,再向塔的方向直行40米到达B处,又测得塔顶C的仰角为,请你帮助小明计算出这座铁塔的高度.(小明的身高忽略不计,结果精确到,参考数据:,,)20.(本小题满分6分)已知二次函数,自变量的部分取值及对应的函数值如下表所示:x …0 2 …y … 1 11 …(1)求这个二次函数的解析式;(2)写出这个二次函数图象的顶点坐标.(3)若>0,且,两点都在该函数的图象上,试比较与的大小.21.(本小题满分5分)如图,⊙∥CD,交AC的延长线于点E.连接BC.(1)求证:BE为⊙O的切线;(2)如果CD=6,tan∠BCD=,求⊙O的直径的长.22.(本小题满分5分)已知:正方形中,,绕点顺时针旋转,它的两边分别交(或它们的延长线)于点.(1)当绕点旋转到时(如图1),线段和之间有怎样的数量关系?请直接写出你的猜想.(2)当绕点旋转到如图2的位置时,线段和之间又有怎样的数量关系?写出猜想,并加以证明.23.(本小题满分5分)已知:关于x的一元二次方程.(1)求证:方程有两个实数根;(2)设m<0,且方程的两个实数根分别为,(其中),若y是关于m的函数,且,求这个函数的解析式;24.(本小题满分8分)已知:在△ABC中,∠ABC=90°,点E在直线AB上,ED与直线AC垂直,垂足为D,且点M为EC中点,连接BM、DM.(1)如图1,若点E在线段AB上,探究线段BM与DM及∠BMD与∠BCD所满足的数量关系,并直接写出你得到的结论;(2)如图2,若点E在BA延长线上,你在(1)中得到的结论是否发生变化?写出你的猜想并加以证明;(3)若点E在AB延长线上,请你根据条件画出相应的图形,并直接写出线段BM与DM及∠BMD与∠BCD所满足的数量关系.25.(本小题满分8分)在平面直角坐标系中,以点为圆心、5为半径的圆与轴相交于点、(点B在点C的左边),与轴相交于点D、M(点D在点M的下方).(1)求以直线为对称轴,且经过点D、C的抛物线的解析式;(2)若点P是这条抛物线对称轴上的一个动点,求PC+PD的取值X围;(3)若E为这条抛物线对称轴上的点,则在抛物线上是否存在这样的点F,使得以点B、C、E、F为顶点的四边形是平行四边形.若存在,求出点F的坐标;若不存在,说明理由.参考答案:一、选择题1.C2.B3.B4.C5.D6.C7.C8.C二、填空题9.10% 10.11.12.三、解答题13.原式=14.解:移项,得……………1分二次项系数化为1,得……………2分配方……………3分……………4分由此可得,……………5分15.解:连结ON. ………………………………………………1分∵OA⊥MN于点B,∴. ………………2分设ON=x,则OB=x-3.在Rt△中,ON2=OB2+BN2,∴…………………………………………………………4分解得,即. ………………………………………5分16.解:AD=3cm,AB=7cm,AC=cm∴……………2分在中,,=.……………3分∴∽……………4分∴∠ABC=∠ACD……………5分17.解:(1)图略………3分(2) 点A旋转到点A1所经过的路线长=…………5分四、解答题18.解:(1)共有12种可能结果. (2)分(2)游戏公平. (3)分∵两X牌的数字都是偶数有6种结果:(6,10),(6,12),(10,6),(10,12),(12,6),(12,10).∴P(彤彤获胜)==. (4)分P(朵朵获胜)= (5)分∴游戏公平.19.解:∵∠CBD=60°,∠CAB=30°,∴∠ACB=30°.∴AB=BC=40.……………2分在Rt△BDC中,∴(米)………4分答:这座铁塔的高度约为.…………5分20.解:(1)依题意,得………………………………2分解得………………………………………………………3分∴为所求. …………………………………………4分(2)顶点坐标为(,).…………………………………………5分(3)因为当时,随着的增大而增大;且>0,,两点都在该函数的图象上,所以>.……………………………… 6分21.解:(1)证明:∵AB是⊙O的直径,M是CD的中点,∴CD⊥AB. (1)分∴∠AMC=90°.∵BE∥CD,∴∠AMC=∠ABE. ∴∠ABE=90°,即AB⊥BE.又∵B是⊙O上的点,∴BE是⊙O的切线. ……………………………………………………… 2分(2)∵M是CD的中点,CD=6,∴CM=CD=3.在Rt△BCM中,,∴BM=. …………………………………………………… 3分又∵AB是⊙O的直径,∠ACB=90°.∵CM⊥AB于M,∴Rt△AMC∽Rt△CMB.∴,∴.∴.∴AM=6. …………………………………………………… 4分∴AB=AM+BM=6+=. ……………………………………………… 5分即:⊙O的直径的长为.22.解:(1).…………1分(2).如图,在DC的上截得DE=MB,连接AE,易证:≌.∴AE=AM.∴∠MAB=∠EAD.∵∠MAN=45°∠BAD=90°∴∠MAN=∠EAN=45°.又AM为公共边,∴≌……………4分∴MN=NE.∴.……………5分23.(1)证明:∵是关于x的一元二次方程, (1)分∵ m2≥0,∴原方程有两个实数根. …………………………………………………2分(2)解:由求根公式,得.∴ x=m+1或x=1. …………………………………………… 3分∵ m<0,∴ m+1<1.∵,∴ x1=m+1, x2=1. ……………………………………………………4分∴.即(m<0)为所求. …………………………………………… 5分说明:若第(1)问直接求出两根,累计得3分;第(2)问没写m<0不扣分;24.解:(1) 结论:BM=DM,∠BMD=2∠BCD. …………………………………2分(2)在(1)中得到的结论仍然成立. 即BM=DM,∠BMD=2∠BCD.证法一:∵点M是Rt△BEC的斜边EC的中点,∴ BM=EC=MC.又点M是Rt△DEC的斜边EC的中点,∴ DM=EC=MC.∴ BM=DM. ……………………………………………………………3分∵ BM=MC, DM=MC,∴∠CBM =∠BCM,∠DCM=∠CDM. …………………………………4分∴∠BMD=∠EMB∠EMD=2∠BCM2∠DCM=2(∠BCM∠DCM)= 2∠BCD. ……………………………………5分即∠BMD=2∠BCD.证法二:∵点M是Rt△BEC的斜边EC的中点,∴ BM=EC=ME.又点M是Rt△DEC的斜边EC的中点,∴ DM=EC=MC.∴ BM=DM. ……………………………………………………………3分∵ BM=ME, DM=MC,∴∠BEC=∠EBM,∠MCD=∠MDC. (4)分∴∠BEM+∠MCD=∠BAC =90°.∴∠BMD=180°(∠BMC+∠DME)=180°(∠BEM+∠MCD)=180°2(90°∠BCD)=2∠BCD.……………5分即∠BMD=2∠BCD.(3)所画图形如图所示:图1中有BM=DM,∠BMD=2∠BCD;图2中∠BCD不存在,有BM=DM;图3中有BM=DM,∠BMD=360°2∠BCD.……………………………………………8分说明:每种情况图形及结论正确各1分.25.解:(1)设以为对称轴的抛物线的解析式为,由已知得点C、D的坐标分别为C(2,0)、D(0,-4),分别代入解析式,得,解得∴为所求. ……………………………………………2分(2)(图1)∵点C(2,0)关于直线的对称点为点B(,0),∴要求PC+PD的最小值,即求线段BD的长.在Rt△BOD中,由勾股定理得,∴PC+PD的最小值是.………………………4分∵点P是对称轴上的动点,∴PC+PD无最大值.∴PC+PD的取值X围是. …………5分(3)存在.①(图2)当BC为平行四边形的一边时,若点F在抛物线上,且使四边形BCFE或四边形BCEF为平行四边形,则有BC∥EF且BC=EF.设点E(-3,t),过点E作直线EF∥BC与抛物线交于点F(m,t).由,得. ∴(7,t),(-13,t).又当时,.∴(7,),(,). ……………………………………………7分②(图3)当BC为所求平行四边形的对角线时,由平行四边形性质可知,点F即为抛物线的顶点(,). (8)分∴存在三个符合条件的F点,分别为(7,),(,),(,).(说明:各解答题不同的解法参照以上标准给分)。
北京市八年级下学期开学数学试卷(II )卷

北京市八年级下学期开学数学试卷(II )卷一、仔细选一选 (共10题;共20分)1. (2分)下列长度线段能组成三角形的是()A . ,,B . ,,C . ,,D . ,,2. (2分)如图,点A的坐标为(-1,0),点B在直线上运动,当线段AB 最短时,点B的坐标为()A . (0,0)B . (,)C . (,)D . (,)3. (2分)给出下列命题:①若a>b,则ac2>bc2;②若ab>c,则b>;③若-3a>2a,则a<0;④若a<b,则a-c<b-c,其中正确命题的序号是()A . ③④B . ①③C . ①②D . ②④4. (2分)当圆的半径发生变化时,圆的面积也发生变化,圆的面积S与半径的关系为S= 下列说法正确的是().A . , ,都是变量B . 只有是变量C . , 是变量,是常量D . ,, 都是常量5. (2分)如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC 的是()A . CB=CDB . ∠BAC=∠DACC . ∠BCA=∠DCAD . ∠B=∠D=90°6. (2分)如图,在△ABC中,AB=AC=5,BC=6,点M为BC边中点,MN⊥AC于点N,那么MN等于()A .B .C .D .7. (2分)等腰三角形的一个内角等于40°,则另外两个内角的度数分别为()A . 40°、100°B . 70°、70°C . 70°、100°D . 40°、100°或70°、70°8. (2分)已知y=(m﹣3)x|m|﹣2+1是一次函数,则m的值是()A . -3B . 3C . ±3D . ±29. (2分)如图,在Rt△ABC中,∠C=90°,按下列步骤作图:①以点B为圆心,适当长为半径画弧,与AB,BC分别交于点D,E;②分别以D,E为圆心,大于DE的长为半径画弧,两弧交于点P;③作射线BP交AC于点F;④过点F作FG⊥AB于点G.下列结论正确的是()A . CF=FGB . AF=AGC . AF=CFD . AG=FG10. (2分)如图,△ABC中,∠ACB=90°,AC>BC,分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG,连接EF、GM、ND,设△AEF、△BND、△CGM 的面积分别为S1、S2、S3 ,则下列结论正确的是()A . S1=S2=S3B . S1=S2<S3C . S1=S3<S2D . S2=S3<S1二、认真填一填 (共6题;共7分)11. (1分)100的算术平方根是________ .12. (1分)在平面直角坐标系中,点A的坐标是(﹣2,3),作点A关于x轴的对称点,得到点A′,再将点A'向右平移3个单位得到点A″,则点A''的坐标是________.13. (1分)观察中国象棋的棋盘,其中“马”的位置可以用一个数对(3,5)来表示,则表示“兵”点位置的数对是________.14. (1分)等腰三角形一腰上的高与另一腰的夹角为36°,则该等腰三角形的底角的度数为________.15. (2分)若不等式组的解集为-1<x<1,则a=________ ,b=________ .16. (1分)如图所示,已知点N(1,0),直线y=﹣x+2与两坐标轴分别交于A,B两点,M,P分别是线段OB,AB上的动点,则PM+MN的最小值是________.三、全面答一答 (共7题;共86分)17. (5分)当k为何负整数时,方程组的解适合x>y?18. (10分)如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.实验与操作:根据要求进行尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法)(1)作∠DAC的平分线AM;(2)作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE,CF.猜想并证明:判断四边形AECF的形状并加以证明.19. (11分)如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).(1)写出点A、B的坐标:A(________,________)、B(________,________)(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′(________,________)、B′(________,________)、C′(________,________).(3)△ABC的面积为________.20. (20分)某商店购进甲、乙两种型号的滑板车,共花费13000元,所购进甲型车的数量不少于乙型车数量的二倍,但不超过乙型车数量的三倍.现已知甲型车每辆进价200元,乙型车每辆进价400元,设商店购进乙型车x辆.(1)商店有哪几种购车方案?(2)若商店将购进的甲、乙两种型号的滑板车全部售出,并且销售甲型车每辆获得利润70元,销售乙型车每辆获得利润50元,写出此商店销售这两种滑板车所获得的总利润y (元)与购进乙型车的辆数x(辆)之间的函数关系式?并求出商店购进乙型车多少辆时所获得的利润最大?(3)商店有哪几种购车方案?(4)若商店将购进的甲、乙两种型号的滑板车全部售出,并且销售甲型车每辆获得利润70元,销售乙型车每辆获得利润50元,写出此商店销售这两种滑板车所获得的总利润y (元)与购进乙型车的辆数x(辆)之间的函数关系式?并求出商店购进乙型车多少辆时所获得的利润最大?21. (20分)如图,直线l1的函数表达式为y1=﹣3x+3,且l1与x轴交于点D,直线l2:y2=kx+b经过点A,B,与直线l1交于点C.(1)求直线l2的函数表达式及C点坐标;(2)求△ADC的面积;(3)当x满足何值时,y1>y2;(直接写出结果)(4)在直角坐标系中有点E,和A,C,D构成平行四边形,请直接写出E点的坐标.22. (10分)尺规作图:作无理数 .作法:①在数轴上点A,B,C分别表示-2,-1,0,分别以点A,B为圆心,AB长为半径画弧,两弧交于点D;②连接CD,以点C为圆心,CD长为半径画弧,交数轴正半轴于点P。
北京市东城区20082009学年度第二学期综合练习

北京市东城区2008—2009学年度第二学期综合练习(一)初三英语学校_____________ 姓名___________ 准考证号___________第I卷(机读卷共70分)第一部分听力(18分)一、听对话,选择与对话内容相符的图片。
每段对话读两遍。
(共4分,每小题1分)请听第一段对话,完成第1小题。
1.请听第二段对话,完成第2小题。
2.请听第三段对话,完成第3小题。
请听第四段对话,完成第4小题。
二、听对话,根据其内容,从下列各题所给的A、B、C三个选项中,选择最佳选项。
每段对话读两遍。
(共14分,每小题1 分)请听第一段对话,回答第5小题。
What does the man want?A. Some flowers.B. Some bananas.C. Some books.请听第二段对话,回答第6小题。
6.Where does the woman want to go?A. The school.B. The post office.C. The library.请听第三段对话,回答第7小题。
7.How is the weather?A. Fine.B. Hot.C. Cold.请听第四段对话,回答第8小题。
8.Who is answering the telephone call?A. Bill.B. Mike.C. Kate.请听第五段对话,回答第9~ 10小题。
9. Why does the man just ask for a piece of apple pie?A. He’s in a hu rry.B. He doesn’t eat much.C. He doesn’t have enough mone y. much will he pay?A. $.B. $.C. $.请听第六段对话,回答第11 ~ 12小题。
is the woman doing on the 13th?A. Having a meeting.B. Seeing her doctor.C. Visiting her friend Ruth.12. When are they going to meet?A. On the fourteenth.B. On the fifteenth.C. On the sixteenth.请听第七段对话,回答第13 ~ 15小题。
北京市东城区2009-2010学年度第二学期综合练习(一)
北京市东城区2009-2010学年度第二学期综合练习(一)高三数学试卷(文科) 2010.4本试卷分第Ⅰ卷和第Ⅱ卷两部分,共150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
参考公式:样本方差])()()[(1222212x x x x x x ns n -++-+-=,其中为样本平均数. 第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.1. 计算复数ii +-11的结果为( )A .i -B .iC .-1D .12.设集合A={1,2,4,6},B={2,3,5},则韦恩图中阴影部分表示的集合 ( ) A. {2} B. {3,5}C. {1,4,6}D. {3,5,7,8}3.已知某几何体的三视图如右图所示,则该几何体的表面积是 ( ) A.226+ B. 26+ C. 225+ D. 25+4.已知变量x,y 满足⎪⎩⎪⎨⎧≤-≤≥021y x y x 则y x +的最小值为( )A.2B.3C.4D.55. 按如图所示的程序框图运算,若输入x=6,则输出k 的值是 A.3 B.4 C.5 D.66.某人向一个半径为6的圆形靶射击,假设他每次射击必定会中靶, 且射中靶内各点是随机的,则此人射中靶点与靶心的距离小于2的 概率为 ( ) A.131 B. 91C.41 D.217.已知圆04122=-++mx y x 与抛物线241x y =的准线相切,则m 的值等于A.2±B. 3C. 2D. 3±8.已知函数)(t f 是奇函数且是R 上的增函数,若x,y 满足不等式)2()2(22y y f x x f --≤-,则22y x +的最大值是A.3B.22C. 8D. 16第II 卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡相应位置的横线上。
北京宣武08-09学年九年级下第二次质量检测试卷二模
北京市宣武区2008-2009学年度第二学期第二次质量检测九年级数学 2009.6一、选择题(共8道小题,每小题4分,共32分) 1.-3的立方是( ) A .-27 B .-9C .9D .272.据统计,2008中国某小商品城市场全年成交额约为348.4亿元.近似数348.4亿元的有效数字的个数是( )A .6个B . 5个C .4个D .11个 3.正方形网格中,AOB ∠如图放置,则cos AOB ∠的值为( )A . 255B .2C .12D . 554.已知甲、乙两组数据的平均数分别是80x =甲,90x =乙,方差分别是210S =甲,25S =乙,比较这两组数据,下列说法正确的是( ) A .乙组数据的波动较小 B .乙组数据较好 C .甲组数据的极差较大 D .甲组数据较好5.某等腰三角形的两条边长分别为3cm 和6cm ,则它的周长为( ) A .9cmB .12cmC .15cmD .12cm 或15cm6.下列四个三角形,与左图中的三角形相似的是( )7. 函数6y x =-与函数()40y x x=>的图象交于A 、B 两点,设点A 的坐标为()11,x y ,则边长分别为1x 、1y 的矩形面积和周长分别为( )A. 4,12B. 4,6C. 8,12D. 8,6 8.如图,在Rt△ABC 中,AB AC =,D 、E 是斜边BC 上两点,且∠DAE =45°,将△ADC 绕点A 顺时针旋转90︒后,得到△AFB ,连接EF ,下列结论: ①△AED ≌△AEF ; ②△ABE ∽△ACD ;(第8题图)AB CDEF(第6题)A .B .C .D .AB O(第3题 )③BE DC DE +=; ④222BE DC DE +=其中一定正确的是 A .②④ B .①③ C .②③ D .①④二、填空题(共4道小题,每小题4分,共16分) 9. 分解因式3244y y y -+= . 10. 函数13y x =-中,自变量x 的取值范围是 . 11. 一个口袋里有4个白球,5个红球,6个黄球,每个球除颜色外都相同,搅匀后随机从袋中摸出一个球,这个球是白球的概率是12. 如图,OA=OB ,A 点坐标是(2,0)-,OB 与x 轴正方向夹角为45︒,则B 点坐标是 . AB 与y 轴交于点C ,若以OC 为轴,将OBC ∆沿OC 翻折,B 点落在第二象限内B '处,则BB '的长度为 .三、解答题(共13道小题,共 72 分) 13.(本小题满分5分) 计算: ︒+-+--3tan60)4(27)21(02π.14.(本小题满分5分) 解方程22011x x x -=+-.15. (本小题满分5分)小明站在A 处放风筝,风筝飞到C 处时的线长为20米,这时第15题图(第12题图)测得∠CBD=60°,若牵引底端B 离地面1.5米,求此时风筝离地面高度。
20092010学年第二学期八年级数学期中试卷
WORD 完整版----可编辑----教育资料分享学校_____________ 班级_________姓名_____________ 考试号__________……………………………………………密……………………………封………………………………线………………………………………2009-2010学年第二学期八年级数学期中试卷(试卷满分:100分;考试时间:120分钟)一、 细心选一选(本大题共9小题,每小题2分,共18分.) 1.如果b a <,下列各式中不.一定..正确..的是…………………………………………【 】A .11-<-b aB .b a 33->-C .b a 11<D .44ba < 2.如果关于x 的不等式2)1(>+x a 的解集为1-<x ,则a ………………………【 】A .3>aB .3-≤aC .3=aD .3-=a3、实数a b ,在数轴上对应点的位置如图所示,则必有……………………【 】 A .0a b +> B .0a b -<C .0ab >D .0ab< 4.下列各式中:①32-π;②a 1;③21x x =;④y x -25;⑤x y x 32-;⑥3x 分式有………………………………………………………………………………………【 】A .1个B .2个C .3个D .4个 5.把分式ba ab+2中的a 、b 都扩大6倍,则分式的值…………………………………【 】 A .扩大12倍B .不变C .扩大6倍D .缩小6倍6.在同一坐标系中,函数xky =和3+=kxy 的图像大致是………………………【】72可能满足8.某服装厂准备加工400套运动装,在加工完160套后,采用了新技术,使得工作效率比原计划提高了20%,结果共用了18天完成任务,问计划每天加工服装多少套?在这个问题中,设计划每天加工x 套,则根据题意可得方程为…………………………【 A .18%)201(400160=++x x B .18%)201(160400160=+-+xx C .18%20160400160=-+xx D .18%)201(160400400=+-+x x 9.如图,Rt △ABC 的直角边BC 在x 轴正半轴上,斜边AC 边上的 中线BD 反向延长线交y 轴负半轴于E ,双曲线)0(>=x xky 的 图象经过点A ,若△BEC 的面积为4,则k 等于……………………………【 】 A .2 B .4 C .8D .16二、认真填一填,要相信自己的能力!(每空2分,共28分)x 时,分式242x x -+值为0.2224315y y x x÷-=(); 11.若一个分式含有字母m ,且当5m =时,它的值为12,则这个分式可以是.(写出一个..即可) 0……………12.反比例函数y=xk(k ≠0)的图象经过点(2,5),若点(1,n )在图象上,则n=. 13.不等式组2494x xx x -<⎧⎨+>⎩的解集是.14.若2,3a b =则23a ba b+=-.已知113x y -=,则代数式21422x xy y x xy y ----的值为. 15.如果关于x 的分式方程xmx x -=--552有增根,则m 的值为. 16.若y 与z 成正比,x 与z 成反比,则y 与x 成.(填“正比”或“反比”) 17.已知等边△ABC 边长为4,D 、E 分别为BC 和AC 上的点,且△ABD ~△DCE ,则∠ADE=度;若点D 为BC 的三等份点,则EC=。
2009-2010第二学期初二数学期末考试题-东城
东城区2009—2010学年度第二学期期末教学目标检测初 二 数 学一.选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 如果1-a 是二次根式,那么a 应满足的条件是( ).A. a ≥0B. a >1 C . a ≥1 D. a ≠1 2. 已知函数xky =的图象过点(1,2),则该函数的图象必在( ). A . 第一、三象限 B. 第二、四象限 C. 第一、四象限 D. 第二、三象限 3. 已知一组数据:2,5,2,3,4,这组数据的中位数是( ). A. 2 B . 3 C. D. 44. 如图,Rt △ABC 中,∠ACB =90°,AC =1,BC =3,则AB 的长为( ).A. 2 B .5 C. 10 D. 22 5. 已知点A (2,1y )、B (3,2y )都在反比例函数xy 3=的图象上,则( ). A . 21y y > B.21y y < C. 21y y = D. 21y y ≤ 6. 把方程x 2-4x+1=0配方后所得到的方程是( ).A. (x -2)2+1=0 B. (x -4)2+5=0 C . (x -2)2-3=0 D. (x -2)2+5= 0 7. 下列命题中正确的是( ). A. 对角线相等的四边形是矩形 B. 对角线互相垂直的四边形是菱形C . 对角线互相平分的四边形是平行四边形 D. 对角线平分每一组对角的四边形是正方形8. 如图,矩形ABCD ,对角线AC 、BD 交于点O ,AE ⊥BD 于点E ,∠AOB =45°,则∠BAE 的大小为( ).A. 15° B . 22.5° C. 30° D. 45°9.“水立方”的游泳池长为50m ,宽为25m ,深为3m. 现以x m 3/min 的速度向池中注水,AB C 第4题AB C DEO第8题注满水池需y min ,则y 与x 函数关系的大致图象为( ). 10. 如图,已知□ABCD 中,点M 是BC 的中点,且AM =6,BD =12,AD =45,则该平行四边形的面积为( ). A .245 B .36 C . 48 D .72 二. 填空题: 本大题共8小题,第11-17小题每题3分,第18小题4分,共25分. 请把答案填在题中横线上.11. 化简:=-2)3( .12.若一元二次方程x 2+mx -2m =0的一个根为1,则m 的值是 . 13. 小张和小李练习射击,第一轮10发子弹打完后,两人的成绩如图所示.根据图中的信息,小张和小李两人成绩的方差关系是2张S 2李S (填“>”、“<”或“=”).14. 已知反比例函数y =x a 2-,当x >0时,y 随x 的增大而增大,则a 的取值范围是_ _.15.如图,BD 是□ABCD 的对角线,点E 、F 在BD 上,要使四边形AECF 是平行四边形,还需要增加的一个..条件是 . 16.如图,A 是反比例函数y =xk图象上任一点,AC ⊥x 轴于点C ,⊿AOC 的面积为3,则k = . 17.下列各数:①2;②12+;③21 ;④21-;⑤211-,其中与12-的乘积是有理数的是 (填上正确答案的序号即可). 18.正方形A 1B 1C 1O ,A 2B 2C 2C 1,A 3B 3C 3C 2,…按如图所示的 方式放置.点A 1,A 2,A 3,…和点C 1,C 2,C 3,…分别在直线 y kx b =+(k >0)和x 轴上,已知点B 1(1,1),B 2(3,2), 则B 3的坐标是______________,B n 的坐标是______________. 三.解答题: 本大题共7小题,共45分.解答应写出文字说明、证明过程或演算步骤.19.计算:(本题每小题4分,共8分)得分 评卷人得分 评卷人第13题 ABCDM第10题第18题yxOC 1B 2A 2C 3 B 1 A 3B 3A 1 C 2第15题 AB CDE F AC O xy 第16题(1)2112+-1821;(2)6)123(32÷+. 20.解方程: (本题每小题4分,共8分) (1)3x 2-4x =1; (2)x (x-4)=8-2x . 21.(本题满分4分)阅读下列材料:正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫格点三角形.老师给小明出了一道题:在如图1所示的正方形网格(每个小正方形的边长为1)中画出格点⊿ABC ,使AB=AC=5,BC =2;小明的做法是:由勾股定理,得AB=AC=2212+=5,BC =2211+=2,于是画出线段AB ,AC ,BC ,从而画出格点⊿ABC .请你参考小明的做法,在如图2所示的正方形网格(每个小正方形的边长为1)中画出一个格点⊿A ’B ’C ’,使A ’B ’=A ’C ’=5,B ’C ’=10.(直接画图,不写过程).图1图2 22.(本题满分4分)如图,在△ABC 中,∠ABC =90°,BM 平分∠ABC 交AC 于点M ,ME ⊥AB 于点E ,MF ⊥BC 于点F . 判断四边形EBFM 的形状,并加以证明. 23.(本题满分6分)2010年5月1日,第41届世界博览会(Expo 2010)在上海举行,这个以“城市,让生活更美好”(Better City, Better Life )为主题的世博会将创造世界博览会史上最大规模记录,也引来了数以万计的参观者.经世博会官网记录,开幕初期连续八天的每日入园人数如下表:(1) 根据以上图表分析,表中数据的中位数是________,众数是________,平均数是________.(2) 如果保持此入园人流量,请你估计,在184天会期中世博会将接待多少名参观者? (3) 为了分散热门场馆人流,减少排队时间,同时保证最大可能的满足参观者的需求,组织者为参观者提供热门场馆分时预约服务. 如果每天发放的预约券为29万张,你认为能满足参观者的需求吗?如果不能满足,那么你认为每天发放多少张预约券更. 24.(本题满分7分)如图在梯形ABCD 中,AD ∥BC ,AB=AD=DC , 60C ∠=°,AEBD ⊥于点E ,F 是CD 的中点,连结EF .(1) 求证:四边形AEFD 是平行四边形;(2)若AB =2,点G 是BC 边上的一个动点,当点G 在什么位置时,四边形DEGF 是矩形?并求出这个矩形的周长;(3) 在BC 上能否找到另外一点G ‘,使四边形DEG ’F 的周长与(2)中矩形DEGF.25.(本题满分8分)如图,已知直线y =33x 与双曲线y =xk交于A 、B 两点,且点A 的横坐标为3. (1)求k 的值; (2)若双曲线y =xk上点C 的纵坐标为3,求⊿AOC 的面积; (3)在坐标轴上有一点M ,在直线AB 上有一点P ,在双曲线y =xk上有一点N ,若以O 、M 、P 、N 为顶点的四边形是有一组对角为60°的菱形,请写出所有满足条件的点P 的坐标.注18题每空2分, 三、解答题(共45分) 19. (本题每小题4分,共8分) 解:(1)2112+-1821= 2232232-+ ………………………………3分 = 232-. ………………………………4分(2)6)123(32÷+ = 61)3266(⨯+ ………………………………2分= 6+2. ………………………………4分 20.(本题每小题4分,共8分)(1)3x 2-4x =1;解: 3x 2-4x -1=0, ………………………………1分 372612164±=+±=x , ………………………………3分372,37221-=+=x x . ………………………………4分 (2)x (x-4)=8-2x .解: ,2842x x x -=-………………………………1分,0822=--x x ………………………………2分 ,0)2)(4(=+-x x ………………………………3分2,421-==x x . ………………………………4分用其他方法相应给分.21.(本题满分4分)只画出其中一个⊿A ’B ’C ’即可. 22.(本题满分4分)答:四边形EBFM 是正方形. ………………………………1分 证明:在⊿ABC 中,∠ABC =90°,ME ⊥AB 于点E ,MF ⊥BC 于点F , ∴ ∠MEB =∠MFB =90°.∴ 四边形EBFM 是矩形. ………………………………2分 ∵ BM 平分∠ABC ,∴ ME= MF . ………………………………3分 ∴ 四边形EBFM 是正方形. ………………………………4分 23.(本题满分6分)(1) 30,24和34, . ………………………………3分 (2) 5428184.529=⨯(万人) ………………………………4分 (3) 不能满足.因为29小于平均数和中位数.理由略. ………………………6分注:实际上世博会的预约券是预约时打印产生的,学生的回答只要能根据数据设定合理的参考值即可. 24.(本题满分7分)(1) 证明: ∵梯形ABCD 为等腰梯形.AD ∥BC ,∠C =60°,∴120BAD ADC ∠=∠=o . 又∵AB AD =,∴30ABD ADB ∠=∠=o . ∴30DBC ADB ∠=∠=o .∴90BDC ∠=o .由已知AE BD ⊥,∴∠AED =90°.∴AE ∥DC . ········································ 1分 又∵AE 为等腰三角形ABD 的高, ∴E 是BD 的中点.∵F 是DC 的中点, ∴EF ∥BC . 即 EF ∥AD . ·································· 2分 ∴四边形AEFD 是平行四边形. ··································· 3分 (2)当点G 在BC 的中点时,四边形DEGF 是矩形. ……………………………4分 在Rt ⊿BCD 中,∠DBC =30°,CD =2, ∴ BC =4. 由勾股定理,得 BD =23.∴ 矩形DEGF 的周长为2DE +2DF =BD+CD =23+2. ……………………………5分 (3)作DG ’⊥BC 于点G ’,连结EG ’、FG ’. ……………………………6分 ∵ E 是BD 的中点, F 是DC 的中点, ∴ EG ’=21BD=DE ,FG ’=21CD=DF .即四边形DEG ’F 的周长与(2)中矩形DEGF 的周长相等. ……………………………7分 注:其他方法相应给分. 25.(本题满分8分) 解:(1)∵直线y =33x 与双曲线y =xk交于A 点, ∴ 把点A 的横坐标3带入y =33x ,得y=1 .把点A (3,1)带入y =xk,得 k =3. ………………………………2分(2)∵双曲线y =x3上点C 的纵坐标为3, ∴ C (33,3). ………………………………3分 如图,分别过点A 、C 作x 轴的垂线段AE 、CD ,垂足分别为E 、D ,CD 交直线AB 于点F . ∵ AOE COD S S ∆∆=.∴ AFDE COF S S 梯形=∆. ………………………………4分 ∴ =∆AOC S ACDE S 梯形=21×(1+3)×(3-33) =334. ………………………………5分 (其他解法相应给分) (3)点P 的坐标分别为(3,3)、(1,33)、(-3,-3)、(-1,-33). ………………………………8分注:(3)问答对一个给1分,或错一个扣1分.xx。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京八中2009—2010学年度第二学期开学测试
高一数学 2010.2
一、选择听
1.与0
405终边相同的的角是
A. )(4536000Z k k ∈-⋅
B. )(40536000Z k k ∈-⋅
C. )(4536000Z k k ∈+⋅
D. )(4518000Z k k ∈+⋅ 2. 设a 为非零向量,λ是非零实数,下列命题中是真命题的是 A. a 与a λ-方向相反 B. a a ||||λλ≥- C. a a ||||λλ=- D. a 与a λ-方向相同 3.已知0
066sin ,78sin 则a =的值为
A.a 2
B. 2
1a - C. 122
-a D. 2
21a -
4.在四边形ABCD 中,b a b a b a BC b a AB ,,35,4,2且--=--=+=不共线,则四边形ABCD 为 A.平行四边形 B.矩形 C.梯形 D.菱形
5.若5
3
)sin()cos(cos )sin(=
+⋅-+⋅-x y x x y x π,则有 A. 2572cos ,25242sin ==y y B. 257
2cos ,25242sin =-=y y C. 2572cos ,25242sin ±=±=y y D. 25
72cos ,25
24
2sin =±=y y 6.已知),2
cos()(),2
sin()(π
π
-
=+
=x x g x x f 则下列结论中正确的是
A.函数)()(x g x f y ⋅=的周期为π2
B.函数)()(x g x f y ⋅=的最大值为1
C. 函数)
()
(x f x g y =
是单调递增函数 D.将)(x f 的图象向右平移2π个单位后得得图象
7. 将函数)sin()(x x f y ⋅=的图象向右平移
4
π
个单位,再做关于x 轴的对称变换,得到x y 2sin 21-=的图象,则)(x f 可以是 A. x cos B. x cos 2 C. x sin D. x sin 2 8.下列各向量中,能作为表示它们所在平面的所有向量的基底的是 A.)2,1(),0,0(21-==e e B. )7,5(),2,1(21=-=e e C. )10,6(),5,3(21==e e D. )4
3,21(
),3,2(21-=-=e e 9.已知函数4
),0,(cos sin )(π
=∈≠-=x R x a b a x b x a x f 在为常数,
处取得最小值,则函数)4
3
(x f y -=π是
A.偶函数且它的图象关于点)0,(π对称
B. 偶函数且它的图象关于点)0,2
3(π对称 C.奇函数且它的图象关于点)0,2
3(π对称 D. 奇函数且它的图象关于点)0,(π对称 二、填空题 10.扇形中心角为
3
π
,则扇形的内切圆的面积与扇形面积之比为 ; 11.已知x
x
x f +-=
11)(,若),2(ππα∈,则=-+)cos ()(cos ααf f ;
12.=-)310(tan 40sin 00 ;
13. )(x f 是以5为周期的奇函数,===-)2cos 4(,2
1
cos ,4)3(ααf f 则且 ; 14. 函数m x x y +-=sin 222cos 2的定义域为⎥⎦
⎤
⎢⎣
⎡-4,
ππ,它的最小值为3,则m = ;
15.)1,1(=a ,且a 与b a 2+的方向相同,则b a ⋅的取值范围是 ; 16.给出下列命题:①存在实数1cos sin ,=⋅ααα使成立; ②存在实数23cos sin ,=⋅ααα使;③是偶函数;)22
5s i n (
x y -=π
④直线8
π
=
x 是函数)4
52sin(π
+
=x y 图象的一条对称轴; ⑤若βα,是第一象限角,且βα>,则βαtan tan >。
其中正确命题的序号是 (注:把你认为正确的命题的序号都填上); 17.若BC AC AB 2,2==, 则ABC S ∆的最大值为 ;
18.若⎪⎭⎫
⎢⎣
⎡-
2,6ππ,则)1)(cos 1(sin ++=x x y 的最大值是 ,最小值是 。
19.设),,),22cos ,68(cos ),67cos ,23(cos 0000R t b t a u b a ∈+===则
=⋅b a ,u 的模的最小值为 。
三、解答题
21.已知.5
1cos sin ,02=+<<-x x x π
(1)求x x cos sin -的值;
(2)求
x
x x x x x cot tan 2cos 2cos 2sin 22sin 32
2++-的值.
21.已知)cos(,3
2)2sin(912cos(,2
0βαβαβ
απαπ
β+=--=-
<<<
<求,)且的值.
北京八中2009—2010学年度第二学期开学测试
高一数学参考答案
一、填空题
10.3:2 11.
αsin 12.-1 13.-4 14. 2
15.[)+∞-,1 16. ③④ 17. 22 18. 223+, 43323+ 19. 2
2
20.解:(1)
25
12
cos sin 1
cos sin 251)cos (sin 5
1cos sin 222-
=∴=+=
+∴=
+x x x x x x x x 又
5
7cos sin 0cos sin 0
2
25
4925241cos sin 2cos sin )cos (sin 222-
=-∴<-∴<<-
=+
=-+=-x x x x x x x x x x x π
(2)原式=)cos )(sin sin 12
sin
2(2
x x x x
-+ 125
108)2512
(59)
cos )(sin 5
1
2()
cos )](sin cos (sin 2[-=-⨯=-=+-=x x x x x x 21.解:91)2cos(-=-β
α 3
2
)2sin(=-βα
且,2
0παπ
<<<
<x
9
5
48180)91(1)2sin(2=
=--=-
∴β
α 3
5
)32(1)2cos(
2=
-=-βα
)]2
(
)2
[(2βα
β
αβα---
=+
1
)]2
(
)2
[(cos 212
)
(cos 2)cos(22
----
=-+=+∴βα
β
αβαβα
又)2
sin(
)2
sin()2
cos(
)2
cos()]2
(
)2
cos[(βα
β
αβα
β
αβα
β
α--
+--
=---
27
573
29543591=⋅
+⋅-=
729
239
1)2757(2)cos(2-
=-=+∴βα。
