天津预赛试题
2018年全国高中数学联赛天津赛区预赛试题+答案

x3 − 17x − 18 = 0
−4 < x1 < −3 4 < x3 < 5.
1
x2
2 arctan x1 + arctan x2 + arctan x3 .
解析
x1, x2, x3
x3 − 17x − 18 = (x − x1)(x − x2)(x − x3)
x1 + x2 + x3 = 0, x1x2 + x2x3 + x3x1 = −17, x1x2x3 = 18
14. A, B
F1, F2 O
x2 − y2 = 1 4
1 |OA| · |OB| = |OF1|2
2 F1, F2, A, B
.
第6页
解析 1
AB
√
|OA| = |OB| = 5 = |OF1|
AB
.
AB
y = kx + b
x2
−
1 (kx
+
b)2
=
1
4
A, B AB
(1, 2), (1, −2) x
.................................................................... 5
1 x1 ∈ (−4, −3) x3 ∈ (4, 5)
x2 = −x1 − x3 ∈ (−2, 0).
f (x) = x3 − 17x − 18
f (0) = −18 < 0, f (−1) = −2 < 0, f (−2) = 8 > 0
=
(x1 +x2 ) (1−x1 x2 )
+
8学年度天津市初二数学竞赛预赛试题
1997-1998学年度天津市初二数学竞赛预赛试题
一.计算6(7+1)(72+1)(74+1)(78+1)+1(的值。
(结果可用幂的形式表示)二.把多项式x3-3x2+(a-2a分解因式
三.求满足1115
6
x y z
++=,且x≤y≤z的所有正整数解。
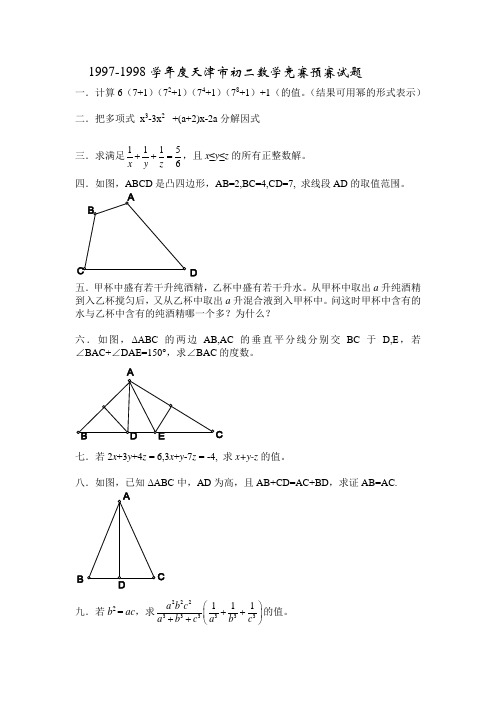
四.如图,ABCD是凸四边形,AB=2,BC=4,CD=7, 求线段AD的取值范围。
D
五.甲杯中盛有若干升纯酒精,乙杯中盛有若干升水。
从甲杯中取出a升纯酒精到入乙杯搅匀后,又从乙杯中取出a升混合液到入甲杯中。
问这时甲杯中含有的水与乙杯中含有的纯酒精哪一个多?为什么?
六.如图,ΔABC的两边AB,AC的垂直平分线分别交BC于D,E,若∠BAC+∠DAE=150°,求∠BAC的度数。
C
七.若2x+3y+4z = 6,3x+y-7z = -4, 求x+y-z的值。
八.如图,已知ΔABC中,AD为高,且AB+CD=AC+BD,求证AB=AC.
B C
九.若b2 = ac,求
222
333333
111
a b c
a b c a b c
⎛⎫
++
⎪
++⎝⎭
的值。
十.三人合办一企业,共投资143万元,投资最多的与投资最少的钱数的比为5:3,问第三个人最多投资多少万元?最少投资多少万元?。
1. 2012年全国高中数学联赛天津预赛

预赛试题集锦(2013)高中竞赛2012年全国高中数学联赛天津市预赛一.选择题(每小题6分,共30分)1.数列{}na的前n项和22nS n n=-,则317a a+=()(A)36(B)35(C)34(D)332.若1x>,则ln ln ln(ln)x xx x-的值是()(A)正数(B)零(C)负数(D)以上皆有可能3.如果ABC△中,A B,为锐角,且22sin sin sinA B C+=,则对ABC△的形状描述最准确的是()(A)直角三角形(B)等腰三角形(C)等腰直角三角形(D)以上都不对4.设椭圆与x轴交于A B,两点,已知对于椭圆上不同于A B,的任意一点P,直线AP与BP的斜率之积均为12-,则椭圆的离心率为()(A(B(C)12(D5.在正四面体ABCD中,M、N分别是BC和DA的中点,则直线AM和BN所成角的余弦值是()(A)13(B)12(C)23(D)346.在半径为1的球面上有不共面的四个点A、B、C、D,且A B C D x==,BC DA y==,CA BD z==,则222x y z++等于()(A)2(B)4(C)8(D)16二.填空题(每小题9分,共54分)7.函数1cos[ππ]y x x=+∈-,,的图象与x轴围成的区域的面积是_______.8.已知ABCDEF是边长为2的正六边形,一条抛物线经过A、B、C、D四点,则该抛物线的焦点到准线的距离是_______.9.如果复数z满足||1z=,且2iz a b=+,其中a、b为实数,则a b+的最大值为_______.10.函数|1||2||10|y x x x=-+-++-的最小值是_______.11.极限222111lim11123n n→∞⎡⎤⎛⎫⎛⎫⎛⎫---=⎪⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦_______.12.如果对一切正实数x、y不等式29cos sin4yx a xy--≥都成立,则实数a的取值范围是_______.三.解答题(每小题20分,共60分)预赛试题集锦(2013) 高中竞赛13. 如果双曲线的两个焦点坐标分别为1(20)F -,和2(20)F ,,双曲线的一条切线交x 轴于102Q ⎛⎫⎪⎝⎭,,且斜率为2.(1)求双曲线的方程;(2)设该切线与双曲线的的切点为P ,求证:12F PQ F PQ ∠=∠.14. 电脑每秒钟以相同的概率输出一个数字1或2.将输出的前n 个数字之和被3整除的概率记为n P .证明:(1)11(1)2n n P P +=-;(2)201213P >.15. 已知三次函数32()4f x x ax bx c =+++(其中a b c R ∈,,)满足:当11x -≤≤时,1() 1.f x -≤≤求a 、b 、c 的所有可能取值.参考答案:1、C .解析:当1n >时,123n n n a S S n -=-=-.因此,31734a a +=2、B .解析:设ln y x =.则y x e =.故原式ln ()0y y y e y =-=3、A .解析:若2A B π+>.则sin cos ,sin cos .A B B A >>故22sin sin sin cos sin cos sin A B A B B A C+>+=矛盾.同理,2A B π+<时,也矛盾,故2A B π+=4、D .解析:不妨设(1.0),(1,0),(,)A B P x y -.则AP l 的斜率为1y x -,BP l 的斜率为1yx +,故1112y y x x ⋅=--+.故椭圆方程为2221x y +=,e = 5、C .解析:不妨设正四面体的棱长为 1.则111,,,022AB AB AB DB AC AB AC DB ⋅=⋅=⋅=⋅=,而11(),()22AM AB AC NB AB DB =+=+ ,故12A M NB ⋅= ,又A M N B == 故AM 与BN 所成角余弦值为236、C .解析:构造一个长方体,使得四面体ABCD 的六条棱分别是长方体某个面的对角线.其外接球直径为长方体的体对角线.故预赛试题集锦(2013)高中竞赛7、2π.解析:作出四条直线2,,,0y x x yππ==-==,则所给函数的图象落在上述四条直线所围成的长方形内部,且关于y轴对称.在第一象限内的部分,函数图象关于点,12π⎛⎫⎪⎝⎭成中心对称,因此,这部分函数图象与x轴、y轴所围成区域的面积等于相应长方形面积的一半.从而,整个函数图象与x轴围成的区域面积为前述长方形面积的一半.即为2π.8.解析:建立平面坐标系,使得((1,0),(1,0),A B C D--.则可求得该抛物线方程为21x=-.92222211()2()2z a b a b a b=⇒+=⇒+≤+=,故当a b==()maxa b+=10、25.解析:注意到,110(1)(10)9x x x x-+-≥---=且等号当[]1,10x∈时成立.同理,297,,561x x x x-+-≥-+-≥,且等号分别当[][]2,9,,5,6x x∈∈时成立.因此,97125y≥+++=,且当[]5,6x∈时等号成立.故所求最小值为25.11、12.解析:12、[]3,3-.解析:依题意知29cos sin4yx a xy+≤+对一切正实数,x y成立.则不等式的左端比小于或等于右端的最小值3.令sint x=.故[]22(1,1)t at t-+≤∈-.取1t=-,得3a≥-;取1t=,得3a≤.当[]3,3a∈-时,易证对任意的[]1,1t∈-均有22t at-+≤成立.因此,[]3,3a∈-.三、13.解法一.设双曲线方程为22221x ya b-=.由于其与直线12()2y x=-,即21y x=-相切,则联立方程组2222121x ya by x⎧-=⎪⎨⎪=-⎩只有唯一一组解.故关于x的方程2222(21)1x xa b--=有两个相等的实根.其判别式0∆=,化简得:22410b a-+=.又2c=则224a b+=.故221,3a b==,双曲线方程为2213yx-=.可解得切点(2,3)P.因此.直线1F P的斜率为131tan412t kk F PQkt-=⇒∠==+,其中,2t=是切线PQ的斜率.又点2F与P的横坐标相同,则2F P∥y轴.故2121211tan tan tan2F PQ F PQ F PQ F PQ F PQt∠==⇒∠=∠⇒∠=∠.解法 2 设双曲线方程为22221x ya b-=.由2224c a b=⇒+=,设点00(,)P x y.则过P的切线方程为00221x x y ya b-=,与所给的切线方程12()2y x=-比较知:22002,x a y b==.代入双曲线方程得:2241a b-=,预赛试题集锦(2013) 高中竞赛可解得221,3a b ==,双曲线方程为2213y x -=.从而,切点坐标为:2200(,)(2,)(2,3)x y a b ==.余下同解法一.14、证法一:这n 个数字共有2n 种可能情形.设其中数字和被3整除的有n x 种.则不被3整除的有2n n x -种.对于1n +各数字的情形,若其和被3整除,则前n 个数字之和不被3整除;反之,对于前n 个数字之和不被3整除的每种情形,有唯一的第1n +个数字可使前1n +个数字之和被3整除.因此,12n n nx x +=-.这表明,概率2nn nx p =满足递推关系式201111201211111111(1)()()()()02323323n n n n p p p p p p ++=-⇒-=--⇒-=-->.所以201213p >.证法二:若输出的前n 个数字之和被3整除的概率为n p ,则不被3整除的概率为1n p -.要使输出的前1n +个数字之和被3整除,则必须使前n 个数字之和不被3整除,且此时第1n +个数字也随之确定.所以,由条件概率的公式得11(1)2n n p p +=-,余下同证法一.证法三:n 个数字共有2n 种可能情形.下面计算其和被3整除的种数,这等于多项式2()()n f x x x =+的展开式种36,,x x 等项的系数之和,即1((1)()())3f f f ωω++.其中,12ω=-+为三次单位根,ω是其共轭复数.故11((1)()())22(1)33n nf f f ωω⎡⎤++=+-⎣⎦.因此,所求的概率为1112()32n n p ⎡⎤=+-⎢⎥⎣⎦,可验证11(1)2n n p p +=-及201213p >.15、由题意,当11,2x =±±时,均有1()1f x -≤≤,故141a b c -≤+++≤,①141a b c -≤-+-≤,②111242a bc -≤+++≤,③ 111242a bc -≤-+-≤.④ ①+②得28223b b -≤+≤⇒≤-;③+④得2123b b -≤+≤⇒≥-,因此,3b =-代入不等式①至④得0,04aa c c +=+=,从而,0a c ==下面证明:3()43f x x x =-满足条件.事实上,若11x -≤≤,则令cos ()x t t R =∈. 故3()(cos )4cos 3cos cos3f x f t t t t ==-=,又1cos31t -≤≤,则1()1f x -≤≤. 综上,0,3,0a b c ==-=。
2007年全国高中数学联赛天津赛区预赛(含详细答案)

2007年全国高中数学联赛天津赛区预赛(含详细答案)一、选择题(每小题6分,共36分)1.方程6)5)(2()4)(1(33=-++-+x x x x 的实数解的个数为( )A .0B .1C .2D .大于2 2.正2007边形P 被它的一些不在P 内部相交的对角线分割成若干个区域,每个区域都是三角形,则锐角三角形的个数为( )A .0B .1C .大于1D .与分割的方法有关 3.已知关于参数a (0>a )的二次函数aa a x a ax y 414131222+--+-+=(R x ∈)的最小值是关于a 的函数)(a f ,则)(a f 的最小值为( )A .-2B .64137-C .41- D .以上结果都不对 4.已知b a ,为正整数,b a ≤,实数y x ,满足)(4b y a x y x +++=+,若y x +的最大值为40,则满足条件的数对),(b a 的数目为( )A .1B .3C .5D .75.定义区间),(d c ,),[d c ,],(d c ,],[d c 的长度均为c d -,其中c d >.已知实数b a >,则满足111≥-+-bx a x 的x 构成的区间的长度之和为( ) A .1 B .b a - C .b a + D .26.过四面体ABCD 的顶点D 作半径为1的球,该球与四面体ABCD 的外接球相切于点D ,且与平面ABC 相切.若32=AD , 45=∠=∠CAD BAD ,60=∠BAC ,则四面体ABCD 的外接球的半径r 为( )A .2B .22C .3D .32 二、填空题(每小题9分,共54分) 7.若关于y x ,的方程组⎩⎨⎧=+=+10122y x by ax 有解,且所有的解都是整数,则有序数对),(b a 的数目为______________.8.方程2007322=+y x 的所有正整数解为_____________.9.若D 是边长为1的正三角形ABC 的边BC 上的点,ABC ∆与ACD ∆的内切圆半径分别为1r ,2r ,若5321=+r r ,则满足条件的点D 有两个,分别设21,D D ,则21,D D 之间的距离为_______________.10.方程1])9(9)4(4)1(1[32)9)(4)(1()9)(4)(1(33333333=++++++++++++---x x x x x x x x x x x x 的不同非零整数解的个数为_____________.11.设集合},,,,{54321a a a a a A =,},,,,{2524232221a a a a a B =,其中54321,,,,a a a a a 是五个不同的正整数,54321a a a a a <<<<,},{41a a B A = ,1041=+a a ,若B A 中所有元素的和为246,则满足条件的集合A 的个数为_____________.12.在平面直角坐标系中定义两点),(11y x P ,),(22y x Q 之间的交通距离为||||),(2121y y x x Q P d -+-=.若),(y x C 到点)3,1(A ,)9,6(B 的交通距离相等,其中实数yx ,满足100≤≤x ,100≤≤y ,则所有满足条件的点C 的轨迹的长之和为________.三、论述题(每小题20分,共60分)13.已知ABC ∆的外心为O ,90<∠A ,P 为OBC ∆的外接圆上且在ABC ∆内部的任意一点,以OA 为直径的圆分别与AB ,AC 交于点E D ,,OE OD ,分别与PC PB ,或其延长线交于点G F ,,求证G F A ,,三点共线.14.已知数列}{n a (0≥n )满足00=a ,11=a ,对于所有正整数n ,有1120072-++=n n n a a a ,求使得n a |2008成立的最小正整数n .15.排成一排的10名学生生日的月份均不相同,有n 名教师,依次挑选这些学生参加n 个兴趣小组,每个学生恰被一名教师挑选,且保持学生的排序不变,每名教师挑出的学生必须满足生日的月份是逐渐增加或逐渐减少的(挑选一名或两名学生也认为是逐渐增加或逐渐减少),每名教师尽可能多选学生.对于学生所有可能的排序,求n 的最小值.参考答案一、选择题(每小题6分,共36分)16=的实数解的个数为( )。
天津市高中化学竞赛预赛试卷(无答案)

XX市高中化学竞赛预赛试卷(无答案)20XX年XX市高中学生化学竞赛预赛试卷(本试卷共150分,考试时间120分钟)一、选择题(单选,本题包括11小题,每题3分,共33分)1.下列分子中为非极性分子的是().H 2OB .CH 4C .HBrD .CsCl2.下列化合物中为离子型化合物的是().MgF 2B .SiH 4C .CO 2D .BrCl3.下列离子核外电子排布正确的是().Fe 3+3d 34S 2B .Cr 3+3d 2C .Cu 2+ 3d 10D .Mn 2+ 3d 54.请推测下列溶液中具有最低解离度的是().0.1 mol/L HClB .0.01 mol/L HClC .0.1 mol/L HFD .0.01 mol/L HF5.酸性溶液中通入H 2S 气体,不产生硫化物沉淀的离子是().Zn 2+B .Sn 2+C .Bi 3+D .Cd 2+6.298K 时,反应N 2(g)+ 3H 2(g)2NH 3(g)的正反应是放热反应。
在密闭容器中,该反应达平衡时,若加入稀有气体,会出现().平衡右移,氨的产量增加B .平衡状态不变C .平衡左移,氨的产量减少D .正反应速率加快7.在XeF 2分子中,Xe 采取的杂化类型是().spB .sp 3C .sp 3dD .sp 3d 28.下列含氧酸根离子中,具有环状结构的是().B 3O 75ˉB .Si 3O 96ˉC .P 3O 105ˉD .S 4O 62ˉ9.下列各组物质中,哪一组有较好的低温效果().冰B .冰+食盐C .冰+食盐+CCl 2D .冰+食盐+CCl 2·6H 2O10.对下列化合物有关物理性质的比较,给出的结论错误..的是()C C ClHHClC C HCl HCl (CH 3)3C -OH(CH 3)3C -Cl①②③④.偶极矩①>②B .熔点②>①C .沸点④>③D .水溶性③>④11.对下列化合物结构与性质描述正确的是()NHOOOHOHOOOOOHOH NH 2①②.①和②不是同分异构体B .①和②均具酸性和碱性C .①和②均可与溴水作用D .①和②均可发生水解反应二、填空题(本题包括10小题,含21空格,每空2分,共42分)12.请给出化合物Pb 3O 4中各元素的氧化数(态)_______________。
2020年全国高中数学联赛天津赛区预赛试题详细答案

2020年全国高中数学联赛天津赛区预赛试题详细答案一、选择题〔每题6分,共36分〕1.二次函数()232f x x x =-+,那么方程()()0ff x =不同实数根的数目为〔 〕。
()1A ()2B ()3C ()4D答 选D 。
因为()()()()2224323233226103f f x x x x x x x x x =-+--++=-+-,因此有()()2123,433310,0,3,2x x x x x x x ±--+====,因此原方程有4个不同实根。
注 也能够讨论()0f x =根的分布情形。
因为当32x ≤时,函数()f x 单调下降,当32x >时,函数()f x 单调上升,且()0f x =的两个根为1,2,因此当32x ≤时,函数()[]1,1,24f x ⎡⎫∈-+∞⊃⎪⎢⎣⎭,因此()()0f f x =有两个不同实根;当32x >时,函数()[]1,1,24f x ⎛⎫∈-+∞⊃ ⎪⎝⎭,因此()()0f f x =也有两个不同实根。
综上所述,原方程有4个不同实根。
2.抛物线21y ax bx =++的参数,a b 满足2384a ab b +=,那么当,a b 变动时,抛物线的顶点一定在〔 〕上。
()A 抛物线 ()B 双曲线 ()C 圆或椭圆 ()D 直线答 选B 。
抛物线21y ax bx =++的顶点的坐标为24,24b a b a a ⎛⎫-- ⎪⎝⎭,设24,24b a b x y a a -=-=,那么有22,1142b b bx x y a a =-=-=+。
因为0a ≠,因此,a b 满足的条件等价于284b b b a a ⎛⎫+= ⎪⎝⎭,因此有()()()28422422x b x x y +-=-=-,即1xy =。
3.ABC ∆的三边,,BC CA AB 的中点分不为,,L M N ,,D E 分不是,BC AB 上的点,并满足,AD CE 均平分ABC ∆的周长,,P Q 分不是,D E 关于,L N 的对称点,PQ 与LM 交于点F ,假设AB AC >,那么AF 一定过ABC ∆〔 〕。
2020年全国高中数学联赛天津赛区预赛试题详细答案
2020年全国高中数学联赛天津赛区预赛试题详细答案一、选择题〔每题6分,共36分〕1.二次函数()232f x x x =-+,那么方程()()0ff x =不同实数根的数目为〔 〕。
()1A ()2B ()3C ()4D答 选D 。
因为()()()()2224323233226103f f x x x x x x x x x =-+--++=-+-,因此有()()2123,433310,0,3,2x x x x x x x ±--+====,因此原方程有4个不同实根。
注 也能够讨论()0f x =根的分布情形。
因为当32x ≤时,函数()f x 单调下降,当32x >时,函数()f x 单调上升,且()0f x =的两个根为1,2,因此当32x ≤时,函数()[]1,1,24f x ⎡⎫∈-+∞⊃⎪⎢⎣⎭,因此()()0f f x =有两个不同实根;当32x >时,函数()[]1,1,24f x ⎛⎫∈-+∞⊃ ⎪⎝⎭,因此()()0f f x =也有两个不同实根。
综上所述,原方程有4个不同实根。
2.抛物线21y ax bx =++的参数,a b 满足2384a ab b +=,那么当,a b 变动时,抛物线的顶点一定在〔 〕上。
()A 抛物线 ()B 双曲线 ()C 圆或椭圆 ()D 直线答 选B 。
抛物线21y ax bx =++的顶点的坐标为24,24b a b a a ⎛⎫-- ⎪⎝⎭,设24,24b a b x y a a -=-=,那么有22,1142b b bx x y a a =-=-=+。
因为0a ≠,因此,a b 满足的条件等价于284b b b a a ⎛⎫+= ⎪⎝⎭,因此有()()()28422422x b x x y +-=-=-,即1xy =。
3.ABC ∆的三边,,BC CA AB 的中点分不为,,L M N ,,D E 分不是,BC AB 上的点,并满足,AD CE 均平分ABC ∆的周长,,P Q 分不是,D E 关于,L N 的对称点,PQ 与LM 交于点F ,假设AB AC >,那么AF 一定过ABC ∆〔 〕。
全国高中数学联赛天津赛区预赛含解答
二OO 六年全国高中数学联合竞赛(天津初赛)(9月17日上午9:00~11:00)一、选择题(本题共5个小题,每小题6分满分30分)(1)已知函数22)(2+-=ax x x f ,当),1[+∞-∈x 时,a x f ≥)(恒成立,则a 的取值范围是( )(A )12<<-a (B )12≤≤-a (C )23-≤≤-a (D )13≤≤-a(2)已知1>>a b ,0>t ,若t a a x +=,则x b 与t b +的大小关系是( )(A )t b b x +> (B)t b b x +< (C)t b b x += (D )不确定(3)已知一条直线l 与双曲线12222=-by a x (0>>a b )的两支分别相交于P 、Q 两点,O 为原点,当OQ OP ⊥时,双曲线的中心到直线l 的距离d 等于( )(A )22a b ab- (B)22a b ab - (C)ab a b 22- (D )ab a b 22- (4)已知P 为四面体ABC S -的侧面SBC 内的一个动点,且点P 与顶点S 的距离等于点P 到底面ABC 的距离,那么在侧面SBC 内,动点P 的轨迹是某曲线的一部分,则该曲线一定是( )(A)圆或椭圆 (B )椭圆或双曲线 (C )双曲线或抛物线 (D)抛物线或椭圆(5)已知集合B 是集合}100,,2,1{ 的子集,且对任意B x ∈,都有B x ∉2,则集合B 中的元素最多有( )(A )67个 (B)68个 (C )69个 (D )70个二、填空题(本题共6个小题,每小题5分,满分30分)(6)已知椭圆12222=+by a x (0>>b a ),长轴的两个端点为A 、B ,若椭圆上存在点Q ,使 120=∠AQB ,则该椭圆的离心率e 的取值范围是 .(7)在ABC Rt ∆中,c ,r ,S 分别表示它的斜边长,内切圆半径和面积,则Scr 的取值范围是 .(8)已知集合},,,,{54321a a a a a C B A = ,且},{21a a B A = ,则集合A 、B 、C 所有可能的情况有 种.(9)已知)sin 3,cos 2(ααA ,)sin 3,cos 2(ββB ,)0,1(-C 是平面上三个不同的点,且满足关系式BC CA λ=,则实数λ的取值范围是 .(10)在一个棱长为5的正方体封闭的盒内,有一个半径等于1的小球,若小球在盒内任意地运动,则小球达不到的空间的体积的大小等于 .(11)已知d c b a ,,,都是偶数,且d c b a <<<<0,90=-a d ,若c b a ,,成等差数列,d c b ,,成等比数列,则d c b a +++的值等于 .三、解答题(本题共3小题,每小题20分,满分60分,解答应写出文字说明,演算步骤或证明过程)(12)已知数列}{n a 满足p a =1,12+=p a ,20212-=+-++n a a a n n n ,其中p 是给定的实数,n 是正整数,试求n 的值,使得n a 的值最小.(13)已知α、β是关于x 的二次方程0222=--tx x 的两个根,且βα<,若函数14)(2+-=x t x x f . (Ⅰ)求βαβα--)()(f f 的值; (Ⅱ)对任意的正数1x 、2x ,求证:||2|)()(|21212121βααββα-<++-++x x x x x x x x f .(14)将1,2,…,16这16个数未填入如图所示的正方形中的小方格内,每个小方格内填一个数,使每一行,每一列的各数之和各不相等且均能被正整数n (1 n )整除.(Ⅰ)求n 的所有可能的值;(Ⅱ)给出一种符合题意的具体填法(此填法适用于n 的所有可能值).二00四年全国高中数学联合竞赛(天津初赛)试题参考答案及评分标准一、选择题(本题共5个小题,每小题6分满分30分)(1)D (2)A (3)A (4)D (5)A二、填空题(本题共6个小题,每小题5分,满分30分)(6)136<≤e (7))1,222[- (8)500 (9)331≤≤λ (10)33144π- (11)194 三、解答题(本题共3小题,每小题20分,满分60分)(12)【解】令n n n a a b -=+1, ,2,1=n由题设20212-=+-++n a a a n n n ,有201-=-+n b b n n ,且11=b …………5分于是)20()(11111∑∑-=-=+-=-n i n i i i i b b,即)1(2)]1(21[1---+++=-n n n b b n . ∴12)40)(1(+--=n n b n . (※) …………………………………10分 又p a =1,12+=p a ,则21123172012a a p a a a <<-=-+-=.∴当n a 的值最小时,应有3≥n ,1+≤n n a a ,且1-≤n n a a .即01≥-=+n n n a a b ,011≤-=--n n n a a b . ……………………………………… 15分 由(※)式,得⎩⎨⎧-≤--≥--2)41)(2(2)40)(1(n n n n 由于3≥n ,且*N n ∈,解得⎩⎨⎧≤≥4040n n , ∴当40=n 时,40a 的值最小. …………………………………………… 20分(13)【解】(Ⅰ)由书籍,根据韦达容不得有2t =+βα,1-=⋅βα βααβαβααααα22)(2414)(22-==-+-=+-=t f , αβαβββαββββ22)(2414)(22-==-+-=+-=t f ,∴222)()(=-+-=--βααββαβαf f ………………………………………5分 (Ⅱ)已知函数14)(2+-=x t x x f ,∴222)1()22(2)(+---='x tx x x f 而且对],[βα∈x ,0))((2222≤--=--βαx x tx x ,于是0)(≥'x f , ∴函数14)(2+-=x t x x f 在],[βα上是增函数 ……………………………………………10分 注意到对于任意的正数1x 、2x0)(2122121>+-=-++x x x x x x x αβαβα,0)(2112121<+-=-++x x x x x x x βαββα 即ββαα<++<2121x x x x ,同理βαβα<++<2121x x x x . ………………………15分 ∴)()()(2121ββααf x x x x f f <++<,)()()(2121βαβαf x x x x f f <++<, )()()(2121ααββf x x x x f f -<++-<-. 于是)()()()()]()([21212121αβαββααβf f x x x x f x x x x f f f -<++-++<--, ∴)()(|)()(|21212121αβαββαf f x x x x f x x x x f -<++-++. 而||222)()(βααβαβ-=-=-f f , ∴||2|)()(|21212121βααββα-<++-++x x x x x x x x f . ……………………………………20分 (14)【解】(Ⅰ)设i s ,i t (4,3,2,1=i )分别是第i 行,第i 列各数的和,由题意得n a s i i =,n b t i i =,其中i a ,i b ,是8个彼此不同的正整数,因为1361621=+++ ,所以n n b a n t si i i i i i 36)821()()(13624141=+++≥+=+=⨯∑∑==得7≤n . ……………………………………………10分 由i s 是n 的倍数得∑=41i i s 是n 的倍数,即136是n 的倍数. 即1721363⨯=,又1>n ,7≤n ,因此n 的可能值为2或4. ……………………15分 (Ⅱ)符合题意的一种具体填法如图所示.…………………………………………20分。
天津市高中学生化学竞赛预赛试卷
2012年天津市高中学生化学竞赛预赛试卷(本试卷共150分,考试时间120分钟)一、选择题(单选,本题包括11小题,每题3分,共33分)1.C和C两者互为()A.同量素B.核素C.同位素D.同素异形体2.下列分子或离子中键长由大到小的顺序正确的是()A.O2>O2+>O2ˉ>O22ˉB.O2+>O2>O2ˉ>O22ˉC.O22ˉ>O2ˉ>O2>O2+D.O2ˉ>O2+>O22ˉ>O23.下列化合物中,氢键表现最强的是()A.NH3B.H2O C.HCl D.HF4.下列各组元素中,性质最相似的是()A.Mg和AlB.Fe和CoC.Zn和HfD.Ag和Au5.在化工生产中,欲除去ZnSO4溶液中的杂质Fe3+离子,需加入的最佳物质是()A.ZnCO3B.NaOHC.NH4FD.氨水6.下列离子中难以和氨生成氨配合离子的是()A.Co2+B.Fe2+C.Ni2+D.Cu2+7.判断下列离子能共存于酸性溶液中的是()A.MnO4ˉ和Mn2+B.Cr2O72ˉ和CrO42ˉC.Fe3+和IˉD.Ag+和Cr2O72ˉ8.要配制Fe2+的标准溶液,最适宜的方法是()A.纯铁丝溶于稀酸B.FeCl2溶于水C.FeCl3溶液加铁屑还原D.Fe(OH)2加酸溶解9.配合物[Pt(Py)(NH3)ClBr]几何异构体的数目为()A.2 B.3 C.4 D.510.已知:R1-CH=CH-R1 + R2-CH=CH-R2Mo卡宾型催化剂1-CH=CH-R21-甲基环己烯与3-甲基-2-戊烯在Mo卡宾型催化剂存在下反应,可得到含13碳的产物种数为()A .2种B .4种C .6种D .8种11.松柏醇结构如下,对它的结构与性质描述错误的是( )A .最多可有21个原子共平面B .既可形成分子内氢键,又可形成分子间氢键C .在水中可与1 mol Br 2反应D .H 2SO 4存在下可与1mol CH 3CO 2H 反应二、填空题(本题包括10小题,含19空,每空2分,共38分)12.BeO 属于__________晶体,其晶格结点上的质点是__________,晶格质点间的作用力是__________。
全国初中数学竞赛天津赛区初赛试题(含答案)
全国初中数学竞赛天津赛区初赛试卷一、选择题⑴若四个互不相等的正实数,,c,a b d 满足()()20122012201220122012a c a d --=,()()20122012201220122012bc bd --=,则()()20122012ab cd -的值为()()A 2012- ()B 2011- ()C 2012 ()D 2011⑵一个袋子中装有4个相同的小球,它们分别标有号码1,2,3,4.摇匀后随机取出一球,记下号码后放回;再将小球摇匀,并从袋中随机取出一球,则第二次取出的球的号码不小于第一次取出的球的号码的概率为()()A 14 ()B 38 ()C 12 ()D 58⑶如图,矩形纸片ABCD 中,3AB =,9AD =,将其折叠,使点D 与点B 重合,得折痕EF ,则EF 的长为()(A )3(B )23(C )10(D )3102⑷在正就变形ABCDEFGHI 中,若对角线2AE =,则AB AC +的值等于()(A 3B )2(C )32(D )52⑸有n 个人报名参加甲、乙、丙、丁四项体育比赛活动,规定每人至少参加 1 项比赛,至多参加2项比赛,但乙、丙两项比赛不能同时兼报,若在所有的报名方式中,必存在一种方式至少有20个人报名,则n 的最小值等于 ( ) (A ) 171 (B ) 172 (C ) 180 (D ) 181二、填空题2x x=-,则221x x -的值为⑺若四条直线1,1,3,3x y y y kx ==-==-所围成的凸四边形的面积等于12,则k 的值为__________.⑻如图,半径为r 的O 沿折线ABCDE 作无滑动的滚动,如果2AB BC CD DE r π====,150,120ABC CDE BCD ∠=∠=∠=,那么,O 自点A 至点E 转动了__________周.(9)如图,已知ABC△中,D为BC中点,,E F为AB边三等分点,AD分别交,CE CF于点,M N,则::AM MN ND等于_______.(10)若平面内有一正方形ABCD,M是该平面内任意点,则MA MCMB MD++的最小值为______.三、解答题⑾已知抛物线2y=x+mx+n经过点(2,-1),且与x轴交于两点A(a,0) B(b,0),若点P为该抛物线的顶点,求使PAB△面积最小时抛物线的解析式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年全国初中学生化学素质和实验能力竞赛(天津赛区)试题参考答案解析一、(每小题2分,共10分)1. A 解析:一定条件下将甲烷、氨气、氢气、水蒸气放在真空容器中有氨基酸的出现,说明有新物质产生,一定发生了化学变化,同时往往伴随有物理变化。
2. C 解析:合成有机高分子材料包括塑料、合成橡胶、合成纤维,也可能引起“白色污染”等环境问题。
3.B 解析:玻璃仪器口部磨砂处理是为了密闭性好,不需要磨砂的仪器一定般不需要考虑密闭性,根据仪器的用途推理就可以知道了选出正确答案。
4. B 解析:CO2不能排出体外,则溶解于体液中显酸性,酸性加增强,PH越减小;食醋是3%-5%的醋酸溶液;蒸馏水可认为是不导电的,因此电解水实验中往往在蒸馏水中加入稀硫酸或氢氧化钠溶液,来增强溶液的导电性,加快反应速率。
5.A 解析:OH-来自碱溶液中,其数目决定于NaOH、KOH的数目。
由于NaOH的相对分子质量较小,因此等体积、等浓度、等密度的两溶液相比,NaOH的个数多,所以所含OH-数目偏多,碱性偏强。
二、(每小题2分,共20分)6.B 解析:块状固体一般存放在广口瓶中。
白磷是一种易自燃的物质,其着火点为40 ℃,但在室温下,因摩擦或缓慢氧化而产生的热量有可能使局部温度达到40 ℃而燃烧。
因此,不能说气温在40 ℃以下白磷不会自燃;白磷是一种剧毒的物质,能挥发产生磷蒸气。
长期吸入磷蒸气,可导致气管炎、肺炎及严重的骨骼损害。
因此不能将白磷露置于空气中。
根据白磷不溶于水,且比水的密度大,可以将少量的白磷放入盛有冷水的广口试剂瓶中,并经常注意保持足够的水量。
通过水的覆盖,既可以隔绝空气,又能防止白磷蒸气的逸出,同时还能保持白磷处于燃着火点之下。
不常用的白磷可以贮存于封口的试剂瓶中,并埋入沙地里。
7. D 解析:实验剩余药品放回试剂瓶可能玷污原试剂,要放入指定容器中;用嘴吹灭酒精灯以可能会引起火灾;用手拿砝码,容易造成腐蚀,引起砝码质量变化,造成称量不准确。
8.A 解析:⑤不能说明CO2的水溶液中含有呈酸性的碳酸。
9.AD 解析:合金属于混合物;合金的熔点比纯金属偏低,硬度、强度偏大;根据化学式特征可知ETFE是一种有机高分子合成材料,不易降解,对环境有污染,但可循环利用;,氮原子最外层电子数为5,容易得到3个电子达到稳定结构,因此氮元素负价态时显-3价,所以氮化镓的化学式为GaN。
10.B 解析: 60℃的甲物质溶液A,恒温蒸发10g水,无晶体析出,说明A为60℃的不饱和溶液且A1可能饱和,再恒温蒸发10g水,5g晶体析出,说明A2一定为60℃的饱和溶液,降温到50℃,析出晶体后,A3是50℃的饱和溶液。
因此如果将A一次恒温蒸发20g水,析出晶体5g;60℃的乙物质溶液B,连续恒温蒸发10g水,都有2g晶体析出,说明B、B1、B2为60℃的饱和溶液,它们的组成相同、质量分数相同,降温到50℃,析出晶体后,B3是50℃的饱和溶液,由于温度不同,因此如果再恒温蒸发10g水,析出晶体质量不一定是2g;60℃的丙物质溶液C, 连续恒温蒸发10g水,无晶体析出,说明C、C1一定为60℃的不饱和溶液且C2可能饱和,降温到50℃,仍无析出晶体后,说明C3是50℃的不饱和溶液与C2的溶液组成相比,没有变化,因此溶质质量分数相同。
且C、C1、C2、C3的组成不同,质量分数不同。
选B当C 、O 2 质量比为1:2即4:8时,密闭容器中气体是CO 2 、CO 的混合气;CH 4 + 2O 2 点燃CO 2 + 2H 2O 1 4当CH 4、O 2质量比为1: 4时恰好完全反应,恢复到常温下密闭容器中气体是CO 2 ,因此容器内的气态物质为纯净物。
12.BD 解析:NaOH 、MgO 中氧元素质量分数相等,是由于它们的分子中所含氧原子数目和两者相对分子质量相等造成的,是化学式计算中的特殊情况,与两者质量是否相等无关;Mn02在2KClO 32KCl+3O 2↑反应中是催化剂,反应前后质量不变,由于KClO 3不断分解产生气体,根据质量守恒定律知,试管中剩余固体质量逐渐减少,则Mn02的质量分数逐渐增大;液体与固体反应,所得溶液质量不一定等于反应物质量总和,关键看是否有气体、沉淀生成,比如碳酸钙与稀盐酸、金属与酸的反应、碳酸钠粉末与石灰水;若设定浓硫酸质量为a,则加入水也为a ,(a ×98%)÷2a= 49%13.A 解析: NH 4HCO 3、KCl 、NH 4Cl 中加入碱液,有氨味产生的说明原物质中含有铵根离子; NH 4HCO 3、NH 4Cl 中加入酸液,有气泡产生的,说明原物质中含有碳酸根离子。
14.A 解析:设H 2SO 4的质量分数为xZn + H 2SO 4 = ZnSO 4 + H 2↑65 98当甲加入6.5gZn 完全溶解时,可能H 2SO 4恰好完全反应或有剩余。
当乙加入13gZn ,加入的Zn 大部分溶解。
说明甲加入6.5gZn 完全溶解时,硫酸有剩余。
若恰好完全反应则H 2SO 4的质量分数为9.8%,所以硫酸的质量分数大于9.8%;当乙加入13gZn 部分溶解时,H 2SO 4完全反应(无剩余),则H 2SO 4的质量分数一定小于19.6%。
当甲加入6.5gZn ,H 2SO 4有剩余时,溶质有硫酸锌和硫酸。
由于乙加入13gZn 部分溶解,所以产生H 2质量小于甲的2倍。
15.BC 解析:①向烧碱溶液中不断加入稀硫酸至过量,PH 由13→7→小于7,图像a 点溶液中含有过量的硫酸,加入Zn 会产生H 2,图示正确;②向氯化钙、盐酸的溶液中加入碳酸钠,碳酸钠先于与盐酸反应,盐酸被反应完后碳酸钠再与氯化钙反应产生沉淀,图示正确。
加入碳酸钠至b 点时,碳酸钠与氯化钙恰好完全反应,所以溶液中的溶质只有氯化钠;③向等质量的盐酸中加入氧化镁、碳酸镁,根据质量守恒定律知,生成氯化镁的质量一定相等,图示错误;④向接近饱和的溶液里加入同种溶质,溶质质量分数逐渐增大至定值,保持不变,图示正确;若饱和溶液溶质质量分数为20%,根据100s s ×100%=20% s=25g 。
三、(本题共23分)16.(每空1分)(1)HCl O 2 (或富含O 2的空气) (2)加热煮沸 热固性 解析:(2)根据铁锅上塑料手柄的用途确定塑料的性能 17.(每空1分)(1)蛋白质、糖类、油脂 蛋白质 (2)元素(3)20 (4)20 解析:(3)100g 食品中含钙元素8mg ,则含碳酸钙质量为:8mg ÷(10040×100%)=20mg(4)油脂得质量为:(2060kJ -20 kJ ×50g -15 kJ ×20g)÷38 kJ/g=20g 18.(6分)(1)(1分)工程塑料 (2)+1 (1分) CO 2 +2LiOH = Li 2CO 3 + H 2O (2分) (3)(2分,每空0.5分)①换气时控制使舱内氮气与氧气的体积比约为4∶1 ②不断地补充氧气③ 吸收呼出的二氧化碳 ④ 吸收排出的水蒸气解析:注意化学式的书写 Li 2CO 3 19. (5分,每空1分)(1)消耗 (2)CO 2+H 2O=H 2CO 3(3)大 深海中,压强大,温度低(4)开发新能源(或减少化石燃料的使用或提高燃料的利用率)解析:气体溶解度受温度、压强的影响。
20.(每空1分)(1)分解反应(2)元素的种类、原子的种类、每种原子的个数、原子的质量、各物质的质量总和(3)(2+m):m解析:(2)质量守恒的本质分析;(3)设原子的质量为X,则原子的质量为mX。
生成物中种物质质量比为:2(2X+mX):2mX=(2+m):m(1×2+m)÷2m=(+2):2m四、(本题共18分)21.(4分,每空1分)(1)通常状况下的气态物质 H2、O2、CO2(2)含氧元素的物质 O2、H2O、CO222. (7分,每空1分)(1)C B A D (2)2HCl + Na2CO3= 2NaCl + H2O + CO2↑2NaOH +CuCl2=Cu(OH)2↓+2NaCl HCl + NaOH = NaCl + H2O解析:(1)注意填写实际的代号。
排放到甲池的废水产生气泡且显酸性,说明是Na2CO3和过量的盐酸反应;乙池产生沉淀且显碱性,说明是CuCl2和过量的NaOH反应。
23. (每空1分)(1)CO2+2NaOH = Na2CO3+ H2O NaOH 氢氧化钙微溶于水,石灰水中溶质含量太少,吸收二氧化碳没有氢氧化钠彻底(2)Mg+2HCl=MgCl2+H2↑镁的金属活动性比铁强(3)溶质质量分数不相同、含同种溶质的两份溶液混合后,总质量等于二者之和溶质质量分数不相同、含同种溶质的两份溶液混合后,总体积不等于二者之和五、(本题共17分)24.(5分,每空1分)(1)K2CO3+Ca(OH)2= CaCO3↓+2KOH (2)过滤(3)CaCl2溶液或BaCl2溶液验证溶液呈碱性前必须将同样显碱性的K2CO3除去。
(4)D解析:本题是一道实验推理与物质转化、除杂、鉴别的综合试题。
步骤①碳酸钙灼烧:CaCO3CaO + CO2↑CaO + H2O =Ca(OH)2放热反应;步骤②K2CO3过量,发生反应:K2CO3+Ca(OH)2=CaCO3↓+2KOH;步骤③过滤,得到沉淀CaCO3和KOH、K2CO3溶液;根据实验目的,最终获得KOH,所以步骤④加入足量的A目的是除去KOH中的K2CO3,将碳酸根离子转化为白色沉淀。
所以A为CaCl2溶液或BaCl2溶液。
这样,溶液中溶质只有KOH。
(4)步骤⑤检验溶液中含有OH-,可以用酚酞试液、Cu2+、Fe3+、Mg2+等。
25. (12分)(1)(4分)(2)(每空0.5分,共6分)(3)(1分)可以通过控制加酸的量(盐酸不必将石灰石浸没)来控制气体的产出量,同时小试管中充满盐酸,可以起到液封的作用,防止气体经漏斗逸出可以减少盐酸用量,节约药品,同时达到液封的目的(4) (1分)气体可被点燃,用一个干燥的烧杯罩在火焰上,烧杯内壁上无水珠出现,再用一个内壁附着有澄清石灰水的烧杯罩在火焰上,烧杯内壁上的石灰水变浑浊 解析:(1)根据实验目的和(2)表格中所留空格可以知道,需要补充4套仪器:BC 用来除去CO 2中的HCl 气体、水蒸气,获得纯净的CO 2;D 与CO 2反应产生CO ;E 排水法收集CO 。
注:饱和碳酸氢钠溶液吸收CO 2中的HCl 气体,是侯氏制碱法的一个原理。
(3)由于锥形瓶体积较大,需要较多的盐酸来浸没长颈漏斗的下口(液封,防止气体经漏斗逸出),用小试管后,可以节约试剂(减少盐酸用量),同时达到液封效果。
