浙江省台州市2009年高三年级第一次调考试题文科数学2009.3
2009年全国1卷高考数学试题(文科)

尽管"开卷有益"是个成语,但我认为:如果盲目开卷,未必有益。
而且古有:尽信书不如无书、纸上谈兵之说。
开卷是否有益,主要还是看谁看书,看什么书和年龄这些因素。
如果是一个心术不正的人看书,不管看什么书,他吸收的总是不好的语言和思想。
相反,是一个素质极好的人看书,他就会有选择性地看书,而且还会去粗取精,把好句好段和好的思想吸收了,不好的语言和思想就会被他排斥。
要是两个心理完全不同的人同样都是看一本警匪书,心术不正的人看了,就会学着做案的手法,而素质极好的人看了,就会学着破案的思维。
看什么书也很重要,看不健康的书,吸收不好的。
就像《蜡笔小新》这本漫画书,我认为这本是给成年人看的休闲读物,而现在看这本书的都是毫无判断是非能力的儿童,学了里面一些不良的语言和习惯。
所以,我觉得开卷是否有益是不能一锤定音的个人觉得,开卷十分有益!读书肯定有好处,但关键还在于你怎么读?这个很有讲究。
还有读什么书也很重要要说开卷一定有益那也未必这要看你开卷看什么书,开电脑干什么事了。
你开卷读好书当然有益,而且是大大的有益;你打开电脑上网、收集资料、写作,当然有益。
如果你看一些内容不好的书或玩电脑游戏,那肯定是无益的1年轻人,不能这么说。
我们看书是要动脑筋的,要带着批判的眼光去读书是对的。
不能尽信书,因为书中也有谬误,尽信书不如无书。
大部分历史书上都是正确的,有谎言的书是存在的,但不会全是谎言。
你说的:“尽量少看历史书!因为都是谎言!”是没有根据的。
所以我不同意你的说法。
赞同沈老师!我很喜欢看历史书读史书可以明志!同样赞同沈老师的说法!!凡事有两面性,看你怎么去看了,呵呵!!世事无绝对的,关键在开卷人的心了。
凡事都有两面性,关键要在什么情况下才能说是好还是错!你想说好,那就好,你想不好,那就不好!反正支持自己这一观点的人,肯定有自己的理由!古人云:“开卷有益。
”确实,博览群书能使人拥有高深的学问,能言善辩,受人尊敬。
【数学】浙江省2009届高三数学文综合卷(1)

浙江省2009届高三文科综合卷(1)一、选择题(每小题5分,共50分)1、已知集合},,1|{},1,0{22A x x y y B A ∈-===则B A = BA .}1,0{B .}1,1,0{-C .}2,11,0{-D .}2,11,0{-- 2、已知点A (1,2).B (3,1),则线段AB 的垂直平分线的方程是BA .524=+y xB 524=-y xC .52=+y xD .52=-y x 3、已知,a b 都是实数,那么22a b >是a b >的 DA .充分不必要条件B .必要不充分条件C .充分必要条件D .不充分不必要条件4、.以141222=-x y 的顶点为焦点,长半轴长为4的椭圆方程为DA .1526422=+y xB .1121622=+y xC .141622=+y xD .116422=+y x5、ABC ∆的三内角,,A B C 所对边的长分别为c b a ,,;设向量),(),,(a c a b q b c a p -+=+=, ,若q p //,则角C 的大小为 DA .6πB .3πC .2πD .23π6、已知m n 、是不重合的直线,αβ、是不重合的平面,下列命题正确的是CA .若,//n m n αβ=,则//,//m m αβB .若//,m m n α⊥,则n α⊥C .若,m m αβ⊥⊥,则//αβD .a b ⊥且b α⊥⇒a ∥α7、若函数)2(+x f =⎪⎩⎪⎨⎧<--≥+0),4lg(0),2sin(x x x x π,则f (3π+2)f (102-)等于CA .21B .21- C .1 D .1-8、已知n S 是等差数列)}({*N n a n ∈的前n 项和,若57S S >,则B俯视图 主视图 左视图第14题图A .076<+a aB .39S S >C .087>+a aD .410S S >9、若直线1x y a b+=与圆221x y +=有公共点,则D A .221a b +≤ B .221a b +≥C .22111a b +≤D .2211a b+≥1 10、下列命题: ①若)(x f 是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,)2,4(ππθ∈, 则(sin )(cos ).f f θθ>②在ABC ∆中,A B >是cos cos A B <的充要条件.③若,,a b c 为非零向量,且a b a c ⋅=⋅,则b c =. ④要得到函数sin2x y =的图像,只需将函数sin()24x y π=-的图像向右 平移2π个单位. 其中真命题的个数有A A .1 B .2C . 3D .4 二、填空题(每小题4分,共28分)11、若命题04,:2>++∈∀c cx x R x p 对为真命题,则实数c 的取值范围是 . (0,1/4) 12、平面上的向量,0,4,22=⋅=+PB PA PB PA PB PA 且满足若向量12,||33PC PA PB PC =+则的最大值为 。
数学文卷·浙江省嘉兴一中2009届高三一模(2009-3)

浙江省嘉兴一中2009届高三一模文科数学 试题卷本测试共三大题,有试题卷和答题卷.试题卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷(选择题)采用机读卡答题的考生请将答案涂写在机读卡上,不采用机读卡的考生请将答案填在答题卷上.第Ⅱ卷(非选择题)答案都填写在答题卷上.第Ⅰ卷一、选择题(本大题共10小题,每题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.己知全集}5,4,3,2,1{=U ,}3,2,1{=A ,}4,3{=B 则=)(B A C U I ( )(A)}3{ (B)}5{ (C)}5,4,2,1{ (D) }4,3,2,1{ 2.向量)1,5(-=x ,),4(x =,⊥,则=x ( ) (A) 1 (B) 2 (C) 3 (D) 4 3.“2=m ”是“直线m x y +=与圆122=+y x 相切”的( )(A)充分而不必要条件 (B)必要而不充分条件(C)充分必要条件 (D)既不充分也不必要条件4.各项都是正数的等比数列}{n a 中,2a ,321a ,1a 成等差数列,则4354a a a a ++的值为( )(A )215- (B )215+ (C )251- (D )215-或215+ 5.若m 、n 为两条不同的直线,α、β为两个不同的平面,则以下命题正确的是( ) (A)若α//m ,α⊂n ,则n m // (B)若α//m ,β⊂m ,n =βαI ,则n m //(C)若α//m ,α//n ,则n m // (D)若m =βαI ,n m ⊥,则α⊥n 6.曲线x y ln =在点))(,(e f e 处的切线方程是( )(A )0=-ey x (B )0=+ey x (C )02=-+e ey x (D )02=+-ey x7.若x 、y 满足约束条件⎪⎩⎪⎨⎧≤≤≤--≥+30030x x y y x ,则x y z 2-=的最小值与最大值的和为( )(A)6 (B)6- (C) 9 (D) 9- 8.函数|1|||ln --=x e y x 的图象大致是( )9.已知4cos 4sin)(xx x f +=,若1x ∃,R x ∈2,使得对R x ∈∀, )()()(21x f x f x f ≤≤ 恒成立,则||21x x -的最小值是( ) (A)π8 (B) π4 (C) π2 (D) π10.P 是椭圆12222=+by a x )0(>>b a 上的一点,F 为一个焦点,且POF ∆为等腰三角形(O 为原点),若满足条件的点P 恰有8个,则椭圆离心率的取值范围为( ) (A) )21,0( (B) )22,21( (C) ),21(+∞ (D) ),22(+∞第Ⅱ卷二、填空题(本大题共7小题,每题4分,共28分) 11.若bi a ii+=-+2121 (a ,R b ∈,i 是虚数单位),则=+b a . 12.命题“对R x ∈∀,02≤++c bx ax ”的否定是 .13.连续两次骰子得到点数分别为m 和n ,记向量),(n m a =,)11(-=b 的夹角为θ,则)2,0(πθ∈的概率为 .14.若⎩⎨⎧--=,1,1)(2x x x f 2112<<--≤≥x x x 或,则函数x x f x g -=)()(的零点为 .15.执行如图所示的框图程序,其输出结果是 .16.某校从参加高二年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[)50,40,[)60,50…[]100,90后画出如下部分频率分布直方图,观察图形的信息,可知这次考试成绩的平均分为 . 17.直线22+-=x y 与曲线14||2||=+y y x x 交点个数为 。
2009届五校高三年级第一次联考文
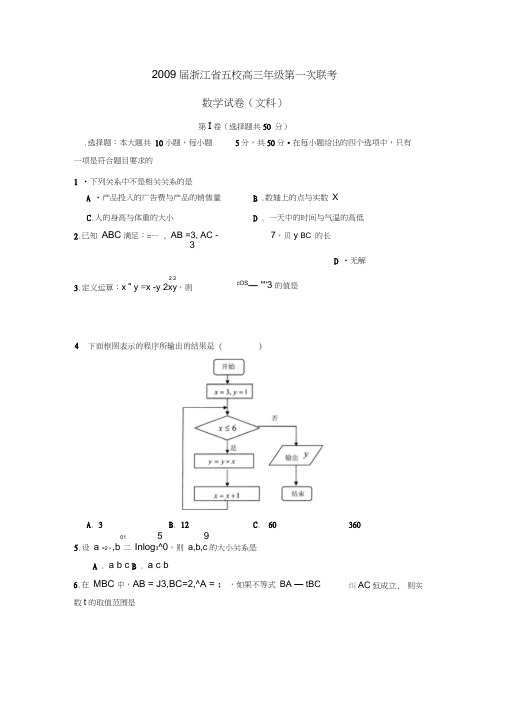
2009届浙江省五校高三年级第一次联考数学试卷(文科)第I 卷(选择题共50 分)一项是符合题目要求的1 •下列关系中不是相关关系的是2.已知 ABC 满足:=— , AB =3, AC - 7,贝y BC 的长3 D •无解2 23.定义运算:x “ y =x -y 2xy ,则01 5 95.设 a =2 • ,b 二 Inlog 3^0,则 a,b,c 的大小关系是A . a b cB . a c b数t 的取值范围是.选择题:本大题共 10小题,每小题 5分,共50分•在每小题给出的四个选项中,只有 A •产品投入的广告费与产品的销售量 B .数轴上的点与实数 XC .人的身高与体重的大小D . 一天中的时间与气温的高低cOS — ""3的值是3606.在 MBC 中,AB = J3,BC=2,^A = ;,如果不等式 BA — tBC 纠AC 恒成立, 则实C . A . 3 B . 12 60 4.D .:;:一匚-J ,o lj 11,-::2 f x =mx -2x1有且仅有一个正实数的零点,则实数 m 的取值范围是( ) -::,1 1D .」:,1a+bi 7 11&已知实数a,b 满足: i 1+i 2 2 前n 项的和,则S n 的最大值是A . 16B . 15C . 14D . 1229.下列命题中:①函数f x ]=sinx x"0,的最小值是2 .. 2 ;②在 ABC 中, 若sin2A=sin2B ,贝U -ABC 是等腰或直角三角形;③函数 f x = e x lnx 的导数是 f ' x 1 ;④如果函数y 二f x 是奇函数,则有 f 0 =0.其中正确的命题是 xA .①②③④B .②③C .②③④D .①④10.设函数f x 二sinxJn x 2 1 x ,对于一a,b^ [0,1,下列结论错误的是 ()f a f bA . 0B . || fa-fba-b_017C . f a]>0D . f b :: 20二 .填空题:本大题共 7小题,每小题4分,共28分.11.某市A 、B 、C 三个区共有高中学生 20000人,其中A 区高中学生9000人,现采用分 层抽样的方法,从这三个区所有高中学生中抽取一个容量为600人的样本进行新课程学习作业量的调查,则 A 区应抽取 ________________ 人.12 .函数 f x =x-x 2 lnx 的单调增区间是 ____________________________ C . 7•函数 C . (其中i 是虚数单位),若用S n 表示数列〈a - bn?的213.如果命题关于x的不等式x - ax V: 0的解集是空集”是假命题,则实数a的取值范围是_________ .14 .从一个装有6个彩色球(3红,2黄,1蓝)的盒子中随机地取出2个球,则两球颜色最小值;—f —f T T(川)若点P 是BC 边上一点,且 AP ・AC =2AP ・AB =2 ,T T T AB +AC +AP 22.(本小题满分15分)已知数列 Sn {的前n 项和为S n ,对一切正整数n ,点(n , S n )都在相同的概率是 _________ • 15•如果实数a,b 满足条件: a b -2 _ 0 b «b — a —1兰0,则一的取值范围是 a <1 16.已知 5s in- - -3s in i 二亠 1 ';],且 tan 〉=xta n :,则实数 x 的值为 ____________17•用lx 1表示不超过x 的最大正数,如 0781-0,301-3,如果定义数列{冷}的通次公 式为「5 =¥ n N *,则 X 1 • X 2 • ||「X 5n 二 解答题 18. (本小题满分14分)已知函数f x 二sinx • cosx , f' x 是f x 的导函数.2 (I)求函数 F X ju f x f ' x f x 的最大值和最小正周期;(n)若 f(x)=2f'(x ),求 tan [x —— 的值.v 4丿 19. (本小题满分14分)把一根长度为 6的铁丝截成3 段. (I)若三段的长度均为整数,求能构成三角形的概率; (n)若截成任意长度的三段,求能构成三角形的概率. 20. 1 3 2 (本小题满分14分)已知函数f x x 3 -ax 2 4x . 3 (|)若曲线y 二f x 在点1,f 1处的切线的倾斜角为 ' 求实数a 的值; 4 21. (II )若函数y = f x 在区间1.0,2 1上单调递增,求实数 a 的取值范围. M 是BC 的中点. (本小题满分15分)在 ABC 中,满足:AB _ AC , AB 二AC ,求向量AB 2AC 与向量2AB AC 的夹角的余弦值; (I )若(II )若O 是线段AM 上任意一点,且 AC 二「2 T T —f —f ,OA OB OC OA 求的 =2,求 的最小值.函数f(X)=2x 2一4的图像上.(I)求数列 a ? 的通项公式;(II)设b n =a n log 2 a n ,求数列b,的前n项的和T ;(川)求证:a-1 ^2 -1 a n^ J •a2_1 a3_1 a4 —1 an 1 _^1 2。
浙江省数学(文科)-2009年高考试题解析

3 千淘万漉虽辛苦,吹尽狂沙始到金。
2 0 0 9
22.(本题满分 15 分)已知抛物线 C : x2 = 2 py( p 0) 上一点 A(m, 4) 到其焦点的距离为 17 . 4 (I)求 p 与 m 的值; (II)设抛物线 C 上一点 P 的横坐标为 t (t 0) ,过 P 的直线交 C 于另一点 Q ,交 x 轴于 点 M ,过点 Q 作 PQ 的垂线交 C 于另一点 N .若 MN 是 C 的切线,求 t 的最小值.
A.1+ i
B. −1+ i
C.1− i
D. −1− i
4.设 , 是两个不同的平面, l 是一条直线,以下命题正确的是( )
A.若 l ⊥ , ⊥ ,则 l
B.若 l / /, / / ,则 l
C.若 l ⊥ , / / ,则 l ⊥
D.若 l / /, ⊥ ,则 l ⊥
要条件.
2 + z2 =
3.设 z = 1+ i ( i 是虚数单位),则 z
()
A.1+ i
B. −1+ i
C.1− i
D. −1− i
3.D 【命题意图】本小题主要考查了复数的运算和复数的概念,以复数的运算为载体,直 接考查了对于复数概念和性质的理解程度.
2 + z2 = 2 + (1+ i)2 = 1− i + 2i = 1+ i
1. B 【命题意图】本小题主要考查了集合中的补集、交集的知识,在集合的运算考查对 于集合理解和掌握的程度,当然也很好地考查了不等式的基本性质.
【解析】 对于 CU B = x x 1 ,因此 A U B = {x | 0 x 1}.
浙江省台州市2009届高三上学期期末考试(数学理)

Equation Chapter 1 Section 1台州市2008学年第一学期高三年级期末质量评估试题数 学(理)注意事项:●本卷所有题目都做在答题卷上.一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集U={1,2,3},且,则集合A 的子集最多有A ∉2A .4个B .5个C .6个D .7个2.若z 是复数,且,则的一个值为i z 432+-=z A .1-2 B .1+2C .2-D .2+i i i i3.b,c a αβ已知,是直线,,是平面,下列命题中正确的是A .B .b ba aαα⊂若//,,则//a a αβαβ⊥⊂⊥若,,则C .D . a a ααββ⊥⊥若,//,则c,b c a a b ⊥⊥若,则//4.等差数列为数列的前项和,则使的的最小值为,}{且n a n S a a a a ,,0,05665>><且}{n a n 0>n S n A .11 B .10 C .6 D .55.已知几何体的三视图(如右图),则该几何体的体积为A .B .344C .D .3243346.在中,若=1,C=, =则A 的值为ABC ∆a ︒60c 3A . B . C . D .︒30︒6030150︒︒或60120︒︒或7. 已知=81010221010,)1()1()1()1(a x a x a x a a x 且+++++++=- A .180B .-180C .45D .-458.已知抛物线的焦点是坐标原点,则以抛物线与坐标轴的三个交点为顶点的三角形的面积)1(2-=x a y 为A .1B .2C .3D .49. 将4名新来的同学分配到A 、B 、C 三个班级中,每个班级至少安排1名学生,其中甲同学不能分配到A 班,那么不同的分配方案有 A. 18种 B. 24种C. 54种D. 60种10.已知函数的定义域为,值域为,那么满足条件的整数对共12||4-+=x y ),](,[Z b a b a ∈]1,0[),(b a 有A .个B .个C .个D .个34592009.01789534567771二、填空题:本大题共7小题,每小题4分,满分28分11. 若命题P :2,10,x R x ∀∈->则命题P 的否定▲ .12. 右边程序框图输出的结果为▲ .13. 已知双曲线的离心率e=2,则其渐近线22221(0,0)x y a b a b-=>>的方程为 ▲ .14. 右图是某学校举行十佳歌手比赛,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数是▲ ,方差是▲ .15. ▲ .22(,1),(2,3),||||x x a ba b a b ==+⋅已知向量则的最大值是16.设是定义在R 上的奇函数,在上有且,则不等式()f x (,0)-∞0)()(<+'x f x f x (2)0f -=的解集为▲ .0)(<x xf 17.设点是内一点(不包括边界),且,则P ABC ∆(,)AP mAB nAC m n R =+∈ 22223m n m n +--+的取值范围是▲ .三、解答题:本大题共5小题,满分72分. 解答须写出文字说明,证明过程和演算步骤.18.(本题满分14分)2()2sin ()2.4f x x x π=-已知函数(1)();(2)()2[0,],6.f x f x m x mπ<+∈求的最小正周期和单调递减区间若在上恒成立求实数的取值范围19. (本题满分14分)某商场在七月初七举行抽奖促销活动,要求一男一女参加抽奖,抽奖规则是:从装有3个白球和2个红球的箱子中每次随机地摸出一个球,记下颜色后放回. 若1人摸出一个红球得奖金10元,1人摸出2个红球得奖金50元. 规定:一对男女中男的摸一次,女的摸二次.令表示两人ξ所得奖金总额.(1)求=20时的概率;ξ(2)求的数学期望.ξ20. (本题满分15分)如图,四棱锥P—ABCD 的底面ABCD 是正方形,侧棱PD ⊥底面ABCD ,PD=DC ,E 是PC 的中点.(1)证明PA//平面BDE ;(2)求二面角B—DE—C 的平面角的余弦值; (3)在棱PB 上是否存在点F ,使PB ⊥平面DEF ?证明你的结论.21.(本题满分15分)如图,已知椭圆的中心在原点,焦点在,且经过点x . 直线交椭圆于两不同的点.(4,1)M :l y x m =+,A B(1);(2);(3),:m l M MA MB x求椭圆的方程求的取值范围22. (本题满分14分)已知= ,数列满足:()f x 2ln 243x x+-{}n a ()()*112,0211N n a f a n a n ∈=<<-++(1)求在上的最大值和最小值;()f x ⎥⎦⎤⎢⎣⎡-021,(2)证明:;102n a -<<(3)判断与的大小,并说明理由.n a 1()n a n N *+∈台州市2008学年第一学期高三年级期末质量评估试题数学(理)参考答案与评分标准一、ABCBC AABBC二、11. 12. 13 13. 14.85,201,2≤-∈∃x R x x y 3±=15.16. 17. (,3) 42{}2002|<<<<-x x x 且23三、18. 解:(1)………………3分()2sin(2) 13f x x π=-++ 最小正周期………………5分T π= 递减区间为………………7分5[,]()1212k k k Z ππππ-+∈(2)0,6x π⎡⎤∈⎢⎥⎣⎦22,333x πππ⎡⎤∴+∈⎢⎥⎣⎦………………10分sin 23x π⎤⎛⎫∴+∈⎥ ⎪⎝⎭⎦………………12分()1,1f x ⎡∴∈-⎣得m 的取值范围是………………14分21m ∴+>()+∞19.对应的事件为:男的摸到红球且女的一次摸到红球,:(1)20ξ=解………………5分23222324(20).555555125P ξ==⨯⨯+⨯⨯=10分1258525252)60(9分12512525253)50(8分12524)20(7分125545352532535352)10(6分12527535353)0()2( =⨯⨯===⨯⨯=====⨯⨯⨯+⨯⨯===⨯⨯==ξξξξξP P P P P ξ010205060P125271255412524125121258=16.85841252100==ξE 且且分14 20. 解(1)以D 为坐标原点,分别以DA 、DC 、DP 所在直线为x 轴、y 轴、z 轴建立空间直角坐标系,设PD=DC=2,则A (2,0,0),P (0,0,2),E (0,1,1),…………2分B (2,2,0) )0,2,2(),1,1,0(),2,0,2(==-=设 是平面BDE 的一个法向量,1(,,)n x y z=则由 ………………4分111001,(1,1,1).2200n DE y z y n x y n DB ⎧⋅=+=⎧⎪=-=-⎨⎨+=⋅=⎩⎪⎩得取得∵ …………5分11220,,//.PA n PA n PA BDE PA BDE ⋅=-=∴⊥⊄∴,又平面平面(2)由(Ⅰ)知是平面BDE 的一个法向量,又是平面DEC 的一个法1(1,1,1)n =- 2(2,0,0)n DA ==向量. ………………7分设二面角B—DE—C 的平面角为,由图可知θ12,n n θ=<>∴121212cos cos ,||||n n n n n n θ⋅=<>===⋅故二面角B—DE—C 的余弦值为………………10分33(3)∵)1,1,0(),2,2,2(=-=∴.,0220DE PB ⊥∴=-+=⋅假设棱PB 上存在点F ,使PB ⊥平面DEF ,设,)10(<<=λλ则,)22,2,2(),2,2,2(λλλλλλ-=+=-=PF DP DF PF由………………13分0)22(244022=--+=⋅λλλλ得∴………………14分PB PF 31)1,0(31=∈=,此时λ即在棱PB 上存在点F ,PB ,使得PB ⊥平面DEF………………15分31=PF 用几何法证明酌情给分21.………………5分.1520,20,5,1116),1,4(,4,23,1)1(:222222222222=+===+===+y x a b b a M b a e by a x 且且且且且且且且且且且且且且且且且且且且且且且且且且222222(2)1584200.205(8)20(420)0,5 5.x y y x m x mx m m m m =++=++-=∆=-->-<<将代入并整理得得121221122121212122112121212211212(3),,0.8420(,),(,),,.5511(1)(4)(1)(4)44(4)(4)(1)(4)(1)(4)2(5)()8(1)2(MA MB k k k k m m A x y B x y x x x x y y y x y x k k x x x x x m x x m x x x m x x m +=-+=-=----+--+=+=----=+--++--=+-+--=设直线斜率分别为和只要证设则分子2420)8(5)8(1)0,55,.m m m m MA MB x-----=因此与轴所围的三角形为等腰三角形22. 解:(1) ()()14ln 4, x f x '=-当时,1-02x <<101-4, ()02x f x '<<∴>在上是增函数………………6分() 3-4 2ln2x f x x ∴=+1-,0 2⎡⎤⎢⎥⎣⎦()()()max min 15f f 02;f f - -ln222x x ⎛⎫∴==== ⎪⎝⎭(2)(数学归纳法证明)①当时,由已知成立;1n =②假设当时命题成立,即成立,n k =102k a -<<………………12分………………10分………………15分那么当时,由①得1n k =+1152()(ln 2,2)2k Qk f a ++=∈-1135ln 22222k a ++<<-<<11112k a +<+< ,这就是说时命题成立.1102k a +∴-<<1n k =+由①、②知,命题对于都成立…………9分n N *∈(3) 由()1111222n n n a a a n f a ++++-=- 记得 ……10分()()12+-=x x f x g ()4ln 4212ln 2)()('1x x x x f x g --=-'=+当故102x -<<121,4 1.2x x <<<<1124102x x --<< 所以 <0 得g(x)在是减函数,)('x g ⎥⎦⎤⎢⎣⎡021-,分12 ∴g(x)>g(0)=f(0)-2=0 ∴>0,即>0()na n a f +-12n n a a ++-+11221得>1+n a n a ……………14分。
2009年浙江高考文科数学试卷及答案解析(精校版)
XC中高考资料绝密★考试结束前2009年普通高等学校招生全国统一考试(浙江卷)数学(文科)本试题卷分选择题和非选择题两部分。
全卷共5页,选择题部分1至3页,非选择题部分4至5页。
满分150分,考试时间120分钟。
请考生按规定用笔将所有试题的答案涂、写在答题纸上。
选择题部分(共50分)注意事项:1.答题前,考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试卷和答题纸规定的位置上。
2.每小题选出答案后,用2B 铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
不能答在试题卷上。
分别表示台体的上、下面积,h 表示台体的高柱体体积公式V Sh=其中S 表示柱体的底面积,h 表示柱体的高锥体的体积公式13V Sh =其中S 表示锥体的底面积,h 表示锥体的高球的表面积公式24S R π=球的体积公式343V R π=其中R 表示球的半径如果事件,A B 互斥,那么()()()P A B P A P B +=+一.选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设{}{},|0,|1,U A x x B x x ==>=>R 则U A B = ð()A .{}|01x x <B .{}|01x x <C .{}|0x x <D .{}|1x x >【测量目标】集合的基本运算(交集与补集).【考查方式】集合的表示(描述法),求集合的补集与交集.【参考答案】B【试题解析】对于{}|1,U B x x =ð因此{}|01U A B x x =< ð.2.“0x >”是“0x ≠”的()A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【测量目标】命题的充分,必要条件.【考查方式】主要考查命题的基本关系以及充分必要条件.【参考答案】A【试题解析】对于“0x >”⇒“0x ≠”;反之不一定成立,因此“0x >”是“0x ≠”的充分而不必要条件.3.设1i z =+(i 是虚数单位),则22z z+=()A .1i+B .1i -+C .1i-D .1i--【测量目标】复数的代数形式的四则运算.【考查方式】给出复数的除法乘方形式,考查复数的代数四则运算.【参考答案】D 【试题解析】对于2222(1i)1i 2i 1i 1iz z +=++=-+=++4.设,αβ是两个不同的平面,l 是一条直线,以下命题正确的是()A .若,,l ααβ⊥⊥则l β⊂B .若,,l ααβ 则l β⊂C .若,,l ααβ⊥ 则l β⊥D .若,,l ααβ⊥ 则l β⊥【测量目标】直线与平面位置关系,平面与平面的位置关系.【考查方式】给出线面,面面的部分关系,推导直线与平面的关系.【参考答案】C【试题解析】对于,,A B D 均可能出现l β ,而对于C 是正确的.5.已知向量(1,2),(2,3)-a =b =.若向量c 满足()()+⊥+ c a b,c a b ,则c =()A .77(,93B .77(,39--C .77(,)39D .77(,93--【测量目标】平面向量的坐标运算.【考查方式】给出平面向量满足的关系式,通过平面向量的平行和垂直关系运算求解.【参考答案】D【试题解析】不妨设(,)m n =c ,则()1,2,(3,1)m n +=+++=-a c a b ,对于()+ c a b ,则有3(1)(2)m n -+=+;(步骤1)又()⊥+c a b ,则有30m n -=,则有77,93m n =-=-(步骤2)6.已知椭圆22221(0)x y a b a b+=>>的左焦点为F ,右顶点为A ,点B 在椭圆上,且BF x ⊥轴,直线AB交y 轴于点P .若2AP PB =,则椭圆的离心率是()A .2B .2C .13D .12【测量目标】椭圆的简单几何性质,解析几何与平面向量结合.【考查方式】考查解析几何与平面向量结合,数形结合求解离心率.【参考答案】D【试题解析】对于椭圆,因为2AP PB = ,则12,2,2OA OF a c e =∴=∴=7.某程序框图如图所示,该程序运行后输出的k 的值是()A .4B .5C .6D .7【测量目标】循环结构的程序框图.【考查方式】考查循环结构的流程图,注意循环条件的设置,以及循环体的构成,特别是注意最后一次循环k 的值.【参考答案】A【试题解析】对于0,1,1k s k ==∴=,而对于1,3,2k s k ==∴=,则2,38,3k s k ==+∴=,后面是113,382,4k s k ==++∴=,不符合条件时输出的4k =.8.若函数2()()af x x a x=+∈R ,则下列结论正确的是()A .a ∀∈R ,()f x 在(0,)+∞上是增函数B .a ∀∈R ,()f x 在(0,)+∞上是减函数C .a ∃∈R ,()f x 是偶函数D .a ∃∈R ,()f x 是奇函数【测量目标】全称量词、存在量词、函数奇偶性与单调性的判断.【考查方式】给出函数式,通过对量词的考查结合函数的性质进行考查.【参考答案】C【试题解析】对于0a =时有()2f x x =是一个偶函数9.已知三角形的三边长分别为3,4,5,则它的边与半径为1的圆的公共点个数最多为()A .3B .4C .5D .6【测量目标】直线与圆的位置关系.【考查方式】通过三角形边与圆相切来考虑公共点.【参考答案】B【试题解析】对于半径为1的圆有一个位置是正好是三角形的内切圆,此时只有三个交点,对于圆的位置稍一右移或其他的变化,能实现4个交点的情况,但4以上的交点不能实现.10.已知a 是实数,则函数()1sin f x a ax =+的图象不可能...是()AB C D【测量目标】三角函数的图象.【参考答案】D【试题解析】对于振幅大于1时,三角函数的周期为2π(步骤1)而D 不符合要求,它的振幅大于(步骤2)非选择题部分(共100分)二、填空题:本大题共7小题,每小题4分,共28分.11.设等比数列{}n a 的公比12q =,前n 项和为n S ,则44S a =.【测量目标】等比数列的通项,等比数列的前n 和.【考查方式】给出等比数列的公比,考查等比数列前n 和每项的关系.【参考答案】15【试题解析】对于4431444134(1)1,,151(1)a q S q S a a q q a q q --==∴==--12.若某几何体的三视图(单位:cm )如图所示,则此几何体的体积是3cm .【测量目标】三视图求几何体的体积.【考查方式】给出三视图,求几何体的体积.【参考答案】18【试题解析】该几何体是由二个长方体组成,下面体积为1339⨯⨯=,上面的长方体体积为3319⨯⨯=,因此其几何体的体积为1813.若实数,x y 满足不等式组2,24,0,x y x y x y +⎧⎪-⎨⎪-⎩则23x y +的最小值是.【测量目标】二元线性规划求目标函数的最值.【考查方式】给出约束条件,应用数形结合思想画出不等式组所表示的平面区域,求出线性目标函数的最小值.【参考答案】4【试题解析】通过画出其线性规划,可知直线23y x z =-+过点()2,0时,()min 234x y +=14.某个容量为100的样本的频率分布直方图如下,则在区间[4,5)上的数据的频数..为.【测量目标】频率分布直方图.【考查方式】给出频率分布直方图,通过图表解决问题.【参考答案】30【试题解析】对于在区间[]4,5的频率/组距的数值为0.3,而总数为100,因此频数为30w.w.w.k.s.5.u.c.o.m15.某地区居民生活用电分为高峰和低谷两个时间段进行分时计价.该地区的电网销售电价表如下:高峰时间段用电价格表低谷时间段用电价格表高峰月用电量(单位:千瓦时)高峰电价(单位:元/千瓦时)低谷月用电量(单位:千瓦时)低谷电价(单位:元/千瓦时)50及以下的部分0.56850及以下的部分0.288超过50至200的部分0.598超过50至200的部分0.318超过200的部分0.668超过200的部分0.388若某家庭5月份的高峰时间段用电量为200千瓦时,低谷时间段用电量为100千瓦时,则按这种计费方式该家庭本月应付的电费为元(用数字作答).【测量目标】分段函数模型.【考查方式】考查识图能力及数据处理能力,求解.【参考答案】148.4【试题解析】对于应付的电费应分二部分构成,高峰部分为500.5681500.598⨯+⨯;对于低峰部分为500.288500.318⨯+⨯,二部分之和为148.416.设等差数列{}n a 的前n 项和为n S ,则4S ,84S S -,128S S -,1612S S -成等差数列.类比以上结论有:设等比数列{}n b 的前n 项积为n T ,则4T ,,,1612T T 成等比数列.【测量目标】等比数列的性质,等差数列的性质.【考查方式】通过已知条件进行类比推理求解.【参考答案】81248T T T T ,【试题解析】对于等比数列,通过类比,有等比数列{}n b 的前n 项积为n T ,则4T ,81248,T T T T ,1612T T 成等比数列.17.有20张卡片,每张卡片上分别标有两个连续的自然数,1k k +,其中0,1,2,,19k = .从这20张卡片中任取一张,记事件“该卡片上两个数的各位数字之和(例如:若取到标有9,10的卡片,则卡片上两个数的各位数字之和为91010++=)不小于14,A ,则()P A =.【测量目标】排列组合及其应用.【考查方式】给出排列组合的方式,求在一定条件下出现A 事件概率.【参考答案】【试题解析】对于大于的点数的情况通过列举可得有5种情况,即7,8;8,9;16,17;17,18;18,19,而基本事件有20种,因此()P A =14三、解答题:本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤.18.(本题满分14分)在ABC △中,角,,A B C 所对的边分别为,,a b c,且满足cos25A =,3AB AC =.(I )求ABC △的面积;(II )若1c =,求a 的值.【测量目标】平面向量的线性运算,正弦定理余弦定理,二倍角,同角三角函数的基本关系.【考查方式】给出关于向量的等式,根据数量积的公式将其转化为边与角的关系式,进而求ABC △的面积;给出边c ,根据余弦定理求a 值.【试题解析】(Ⅰ)531552(212cos2cos 22=-⨯=-=A A (步骤1)又(0,π)A ∈,54cos 1sin 2=-=A A ,(步骤2)而3cos 35AB AC AB AC A === ,所以5=bc ,所以ABC △的面积为:254521sin 21=⨯⨯=A bc (步骤3)(Ⅱ)由(Ⅰ)知5=bc ,而1=c ,所以5=b 所以5232125cos 222=⨯-+=-+=A bc c b a (步骤4)19.(本题满分14分)如图,DC ⊥平面ABC ,EB DC ,22AC BC EB DC ====,120ACB ∠=,,P Q 分别为,AE AB 的中点.(I )证明:PQ 平面ACD ;(II )求AD 与平面ABE 所成角的正弦值.【测量目标】线面平行的判定,线面角的求法.【考查方式】线线平行推出线面平行;由几何体中的位置关系,进行求解.【试题解析】(Ⅰ)证明:连接CQ DP ,,在ABE △中,Q P ,分别是AB AE ,的中点,所以12PQ BE ,(步骤1)又12DC BE,所以PQ DC ,又⊄PQ 平面ACD ,DC ⊂平面ACD ,所以PQ 平面ACD (步骤2)(Ⅱ)在ABC △中,BQ AQ BC AC ===,2,所以AB CQ ⊥(步骤3)而DC ⊥平面ABC ,DC EB //,所以⊥EB 平面ABC而⊂EB 平面ABE ,所以平面ABE ⊥平面ABC ,所以⊥CQ 平面ABE (步骤4)由(Ⅰ)知四边形DCQP 是平行四边形,所以CQDP //所以⊥DP 平面ABE ,所以直线AD 在平面ABE 内的射影是AP ,(步骤5)所以直线AD 与平面ABE 所成角是DAP ∠(步骤6)在Rt APD △中,5122222=+=+=DC AC AD ,1sin 2=∠==CAQ CQ DP 所以5551sin ===∠AD DP DAP (步骤7)20.(本题满分14分)设n S 为数列{}n a 的前n 项和,2n S kn n =+,*n ∈N ,其中k 是常数.(I )求1a 及n a ;(II )若对于任意的*m ∈N ,m a ,2m a ,4m a 成等比数列,求k 的值.【测量目标】等差数列的通项和等比数列的性质,等差数列前n 项和.【考查方式】给出n S 的表达式,求{}n a ;{}n a 中部分项呈等比,求解未知数k .【试题解析】(Ⅰ)当1,111+===k S a n ,2212,[(1)(1)]21n n n na S S kn n k n n kn k -=-=+--+-=-+(○1)(步骤1)检验,,1=n (○1)式成立,12+-=∴k kn a n (步骤2)(Ⅱ)m m m a a a 42,, 成等比数列,224m m m a a a ∴= ,即)18)(12()14(2+-+-=+-k km k km k km ,(步骤3)整理得:0)1(=-k mk ,对任意的*m ∈N 成立,10==∴k k 或(步骤4)21.(本题满分15分)已知函数32()(1)(2)f x x a x a a x b =+--++(,)a b ∈R .(I )若函数()f x 的图象过原点,且在原点处的切线斜率是3-,求,a b 的值;(II )若函数()f x 在区间(1,1)-上不单调...,求a 的取值范围.【测量目标】利用导数判断或求函数的单调区间,函数零点的应用.【考查方式】限定函数的图象过定点处的斜率,解出方程中的未知数;给出函数在区间上的单调性,求未知数的取值范围.【试题解析】(Ⅰ)由题意得)2()1(23)(2+--+='a a x a x x f (步骤1)又⎩⎨⎧-=+-='==3)2()0(0)0(a a f b f 解得0=b ,3-=a 或1=a (Ⅱ)由()0f x '=,得1,x a =(步骤4)又()f x 在(1,1)-上不单调,即2311a a a +⎧≠-⎪⎨⎪-<<⎩或211323a a a +⎧-<-<⎪⎪⎨+⎪≠-⎪⎩(步骤5)解得1112a a -<<⎧⎪⎨≠-⎪⎩或5112a a -<<⎧⎪⎨≠-⎪⎩所以a 的取值范围是11(5,)(,1)22---.(步骤6)22.(本题满分15分)已知抛物线C :22(0)x py p =>上一点(,4)A m 到其焦点的距离为174.(I )求p 与m 的值;(II )设抛物线C 上一点P 的横坐标为(0)t t >,过P 的直线交C 于另一点Q ,交x 轴于点M ,过点Q 作PQ 的垂线交C 于另一点N .若MN 是C 的切线,求t 的最小值.【测量目标】抛物线的简单几何性质,直线与抛物线的位置关系,圆锥曲线中的定点定值问题.【考查方式】给出抛物线上一点到焦点的距离,根据准线方程求方程中未知数;根据直线与抛物线直线与直线的关系,求t 的最小值【试题解析】(Ⅰ)由抛物线方程得其准线方程:2py -=,(步骤1)根据抛物线定义点)4,(m A 到焦点的距离等于它到准线的距离,即41724=+p ,解得21=p (步骤2)∴抛物线方程为:y x =2,(步骤3)将)4,(m A 代入抛物线方程,解得2±=m (步骤4)(Ⅱ)由题意知,过点),(2t t P 的直线PQ 斜率存在且不为0,设其为k .(步骤5)则)(:2t x k t y l PQ -=-,当,,02k kt t x y +-==则)0,(2k ktt M +-.(步骤6)联立方程⎩⎨⎧=-=-y x t x k t y 22)(,整理得:0)(2=-+-t k t kx x 即:0)]()[(=---t k x t x ,解得,t x =或t k x -=(步骤7)))(,(2t k t k Q --∴,而QP QN ⊥,∴直线NQ 斜率为k1-(步骤8))]([1)(:2t k x k t k y l NQ ---=--∴,联立方程⎪⎩⎪⎨⎧=---=--y x t k x kt k y 22)]([1)(整理得:0)()(1122=----+t k t k kx k x ,即:0]1)()[(2=+---+t k k t k x kx 0)](][1)([=--+-+t k x t k k kx ,解得:kt k k x 1)(+--=或t k x -=(步骤9)学诚中高考资料第10页共11页]1)([,1)((22k t k k k t k k N +-+--∴,)1()1(1)(]1)([2222222--+-=+--+--+-=∴k t k kt k kkt t k t k k k t k k K NM (步骤10)而抛物线在点N 处切线斜率:kt k k y k k t k k x 2)(21)(---='=+--=切(步骤11) MN 是抛物线的切线,k t k k k t k kt k 2)(2)1()1(2222---=--+-∴,整理得02122=-++t tk k 224(12)0t t ∆=-- ,解得23t -(舍去),或23t ,32min =∴t (步骤12)如需Word 文档请联系作者索取。
2009届高三调研考试数学试题(文科)2
2009届高三调研考试数学试题(文科)本卷分选择题和非选择题两部分,满分150分.考试用时间120分钟. 注意事项:1. 考生务必将自己的姓名、班级、学校用蓝、黑墨水钢笔签字笔写在答题卷上;2. 选择题、填空题每小题得出答案后,请将答案填写在答题卷相应指定位置上。
答在试题卷上不得分;3. 考试结束,考生只需将答题案交回。
参考公式:锥体的体积公式13V Sh =,其中S 是锥体的底面积,h 是锥体的高. 如果事件A 、B 互斥,那么()()()P A B P A P B +=+.第一部分 选择题(共40分)一、选择题(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合{}{}|1,|21x M x x N x =<=>,则M N =A .∅B .{}|0x x <C .{}|1x x <D .{}|01x x <<2. 复数i 215+的共轭复数为 A.-31035-i B.-i 31035+ C.1-2iD.1+2i3.右图是2008年韶关市举办“我看韶关改革开放三十年”演讲比赛大赛上,七位评委为某位选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为 A.5; 1.6 B.85; 1.6 C.85; 0.4 D.5;0.44.如图, 共顶点的椭圆①,②与双曲线③,④的离心率分别 为1234,,,e e e e ,其大小关系为 A.1234e e e e <<< B.2134e e e e <<<C.1243e e e e <<<D.2143e e e e <<<5.已知()()2,1,1,3-=-=,若()()k ++-∥2,则实数k 的值是A. -17B. 21- C. 1819 D.356.已知两个不同的平面α、β和两条不重合的直线,m 、n ,有下列四个命题 ①若α⊥m n m ,//,则α⊥n ②若βαβα//,,则⊥⊥m m ③若βαβα⊥⊂⊥则,,//,n n m m ④若n m n m //,,,//则=βαα其中正确命题的个数是7984446793② ①④ ③A .0个B .1个C .2个D .3个7.圆074422=+--+y x y x 上的动点P 到直线0=+y x 的最小距离为 A .1 B . 122- C .2 D . 228. 电流强度I (安)随时间t (秒)变化的函数sin()I A t ωϕ=+(0,0,0)2A πωϕ>><<的图象如右图所示,则当1001=t 秒时,电流强度是 A .5-安 B .5安 C . D .10安9.已知函数()21log 3xf x x ⎛⎫=- ⎪⎝⎭,若实数0x 是方程()0f x =的解,且100x x <<,则()1f x 的值为 A .恒为正值B .等于0C .恒为负值D .不大于010. 已知函数()2,f x x bx c =++其中04,04b c ≤≤≤≤.记函数满足()()21213f f ≤⎧⎪⎨-≤⎪⎩的事件为A,则事件A 的概率为 A .58 B .12C .38D .14第二部分 非选择题(共110分)二.填空题(每小题5分,共20分)11. 下面框图表示的程序所输出的结果是___________ .(说明,M N =是赋值语句,也可以写成 M N ←,或:M N =) 12. 在由正数组成的等比数列{}n a 中,12341,4,a a a a +=+= 则56a a +=___. 13. 下列3个命题中①2,210x R x x ∀∈-+>;②“1x >且2y >”是“3x y +>”的充要条件;③函数y =的最小值为2其中假命题的为_________(将你认为是假命题的序号都填上) .第13至15题,从3题中选答2题,多选按前2题记分14.在极坐标系中,圆心在()2,π且过极点的圆的方程为______________15..如图,从圆O 外一点A引圆的切线AD 和割线ABC ,已知AD =6AC =,圆O 的半径为3,则圆心O 到AC 的距离为.三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本题满分12分)在ABC ∆中,c b a 、、为角C B A 、、所对的三边,已知222+c b a bc -=. (Ⅰ)求角A 的值;(Ⅱ)若a =cos 3C =,求c 的长.17.(本题满分12分)现从3道选择题和2道填空题中任选2题. (Ⅰ)求选出的2题都是选择题的概率;(Ⅱ)求选出的两题中至少1题是选择题的概率.18. (本题满分14分)一个棱柱的直观图和三视图(主视图和俯视图是边长为a 的正方形,左视图是直角边长为a 的等腰三角形)如图所示,其中M 、N 分别是AB 、AC 的中点,G 是DF 上的一动点. (Ⅰ)求证:;AC GN ⊥(Ⅱ)求三棱锥F MCE -的体积;(Ⅲ)当FG=GD 时,证明AG //平面FMC.19. (本题满分14分)已知动圆过定点(0,2)F ,且与定直线:2L y =-相切. (I )求动圆圆心的轨迹C 的方程;(II )若A B 是轨迹C 的动弦,且A B 过(0,2)F , 分别以A 、B 为切点作轨迹C 的切线,设两切线交点为Q ,证明:AQ BQ ⊥.20. (本题满分14分)aaa 俯视图左视图主视图GEFNMDCBA已知函数()ln a f x x x=-. (Ⅰ)当0a >时,判断()f x 在定义域上的单调性; (Ⅱ)若()f x 在[1,]e 上的最小值为2,求a 的值.21. (本题满分14分) 已知函数()311,.212x F x x x +⎛⎫=≠ ⎪-⎝⎭(Ⅰ)证明:()()13F x F x +-=,并求122008...;200920092009F F F ⎛⎫⎛⎫⎛⎫+++⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(Ⅱ)已知等差数列{}n a 与{}n b 的前n 项和分别为n S 与n T ,且()nnS F n T =. 当m n >时,比较m m a b 与n nab 的大小; (Ⅲ)在(Ⅱ)条件下,已知12a =,数列{}n b 的公差为2d =.探究在数列{}n a 与{}n b 中是否有相等的项,若有,求出这些相等项由小到大排列后得到的数列{}nc 的通项公式;若没有,请说明理由.。
浙江省绍兴市2009年高三教学质量调研检测文科数学(word版)
3.4 24浙江省绍兴市2009年高三教学质量调研检测数学试题(文科)注意事项:1 •本科考试分试题卷和答题卷,考生须在答题卷上作答。
答题前,请在答题卷的密封线内填写学校、班级、学号、姓名;2 •本试卷分为第I 卷(选择题)和第II 卷(非选择题)两部分,全卷满分150分,考试时间120分钟。
参考公式:如果事件A 、B 互斥,那么棱柱的体积公式V 二 Sh其中S 表示棱柱的底面积,h 表示棱柱的高 棱锥的体积公式1V Sh 3k 其中S 表示棱锥的底面积,h 表示棱锥的高 棱台的体积公式,n ) V = 1 h (S ... S 1S 2 S 2) 3其中S 1, S 2分别表示棱台的上、下底面积, h 表示棱台的高其中R 表示球的半径第I 卷(共50 分)2x2双曲线 y =1的离心率等于J17A .1. 2. 、选择题(本大题共 10小题,每小题目要求的) 若集合 M 二{x|x ::2}, N ={x|x 2 A . [0, 1] B . 0,2 已知数列 5分,共50分。
在每小题给出的四个选项中,只有一项是符合题 — x EO},则M N = C . 1,2 D . :,2 何}中,a 1 =1总=3,当n — 3时,a . = 2nJ ,则此数列前4项和S 4的值为( B . 16C .32 D . 60P(A B)二 P(A) P(B)如果事件A 、B 相互独立,那么P(A B) = P(A) P(B)如果事件A 在一次试验中发生的概率是 P ,那么n 次独立重复试验中恰好发生 次的概率P n (k ) =C :P k (1 -PT' (k=0,1,2,球的表面积公式 S =4 二 R 2 球的体积公式V 球十只3C .4函数y = 3'log? x, X 乏(_oo _1)x ( , 1的值域为X 1,::5 .6. 7 .A. (0, 3)B. [0 , 3]C. :[「匚亠3】已知命题“ x • R,x22ax 1: 0”是真命题,则实数a的取值范围是C.(」:,-1) (1,-:)某程序框图如图所示,则该程序运行后输出的等于(A . 15 C . 31 B. 29D. 63B.D.(1,(—1 , 1)已知定义在R上的函数f (x)关于直线x = 1对称,若f(x) =x(1 -x)(x -1),则f (-2)=C. —6&已知空间两条不同的直线m, n和两个不同的平面:-,A .若m _ : , n〃,:一:,则m _nC.若m〃:, n〃「// l则m//nD . 0,二(第僵)D . —12,则下列命题中正确的是(m _ : , n _ ,:一:,贝U m _ nm〃: , n」",:_ :,则m〃n已知函数y =f(x)定义在[-一,一]上,且其导函数4 4的图象如图所示,则函数y = f (x)可能是(--sin x cosx二sin x cosx=cosx10 .若o是锐角ABC内一点,满足|OA|2|BC|2=|OB|2|CA|2=|OC|2的|AB|2, 则点O是厶ABC ( )A .重心B.垂心 C .内心 D .夕卜心第H 卷(共100 分)二、填空题(本大题共 7小题,每小题4分,共28分) 11 •计算:(2-i )i (i 为虚数单位)的值为 _________ 12.袋中装有大小、形状完全相同的6个红球和3个白球,现从中任取 2个球,则取出的这 2个球是同色的概率等于 ____________ 。
2009年高考浙江数学(文)试题及参考答案
2009年高考试题——数学文(浙江卷)Word版一. 选择题(本大题共10小题,共0分)1. 设,则()A.B.C.D.答案:B2. “”是“”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件答案:A3. 设(是虚数单位),则()A.B.C.D.答案:D4. 设是两个不同的平面,是一条直线,以下命题正确的是()A.若则B.若则C.若则D.若则答案详解加入试题篮收藏回顶部答案:C5. 已知向量a=(1,2),b=(2,-3).若向量c满足(c+a)//b,c⊥(a+b),则c=()A.(,) B.(-,-) C.(,) D.(-,-)答案详解加入试题篮收藏回顶部题目ID:答案:D6. 已知椭圆+=1(a>b>0)的左焦点为F,右顶点为A,点B在椭圆上,且BF⊥F 轴,直线AB交y轴于点P.若=2,则椭圆的离心率是()A.B.C.D.答案:D7. 某程序框图如图所示,该程序运行输出的k的值是()A.4 B.5 C.6 D.7答案:A8. 若函数=+(a R),则下列结论正确的是()A.a R,在上是增函数B.R,在上是减函数C.是偶函数D.是奇函数答案:C9. 已知三角形的三边长分别为3,4,5,则它的边与半径为1的圆的公共点的个数最多为()A.3 B.4 C.5 D.6答案:C10. 已知a是实数,则函数=1+的图像不可能是()A. B.C. D.答案:D二. 填空题(本大题共6小题,共0分)11. 设等比数列的公比,前项和为,则=________答案详解加入试题篮收藏回顶部答案:1512. 若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是________答案:1813. 若实数满足不等式组则的最小值是________ 。
答案:414. 某个容量为100的样本的频率分布直方图如下,则在区间上的数据的频数为________。
某地区居民生活用电分为高峰和低谷两个时间段进行分时计价,该地区的电网销售电价表如下:若某家庭5月份的高峰时间段用电量为200千瓦时,低谷时间用电量为100千瓦时,则按这种计费方式该家庭本月应付的电费为________________元(用数字作答)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙江省台州市2009年高三年级第一次调考试题数 学(文科) 2009.3命题:梅红卫(台州一中) 应福贵(仙居中学)审题:王建华(黄岩中学)注意事项:1. 本卷共4页,三大题,22小题,满分150分,考试时间120分钟; 2. 用蓝、黑色水笔或圆珠笔书写答案,考试结束只需将答案纸交回.参考公式:球的表面积公式 24S πR = 棱柱的体积公式V =Sh球的体积公式 343V πR = 其中S 表示棱柱的底面积,h 表示棱柱的高其中R 表示球的半径 棱台的体积公式121()3V h S S =棱锥的体积公式 V =13Sh 其中S 1, S 2分别表示棱台的上底、下底面积, h 表示棱台的高其中S 表示棱锥的底面积,h 表示棱锥的高 如果事件A ,B 互斥,那么()()()P A B P A P B +=+一.选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 集合M ={}4|2<x x ,N ={}R x x ∈=αα,sin |,则N M = (A )()2,2- (B )()1,1-(C )[]1,1-(D )∅2. 已知不等式0322<--x x 的整数解构成等差数列{n a },则数列{n a }的第四项为(A )3(B )1- (C )2 (D )3或1-3. 已知点(3,1)和原点(0,0)在直线310x ay -+=的两侧,则实数a 的取值范围是 (A )(,10)-∞ (B )(10,)+∞ (C )(,9)-∞ (D )(9,)+∞4. 已知点)0,3(M ,椭圆1422=+y x 与直线)3(+=x k y 交于点A 、B ,则ABM ∆的周长为 (A )4 (B )8 (C )12 (D )165. 已知向量→→b a ,的夹角为0120,51==则=-→→b a 3(A ) 7 (B ) 6 (C )5 (D )46. 一个空间几何体的三视图及部分数据如图所示, 则这个几何体的体积是俯视图侧(左)视图正(主)视图(A )12 (B )1(C )23(D )27. 现要完成下列3项抽样调查:①从10盒酸奶中抽取3盒进行食品卫生检查.②科技报告厅有32排,每排有40个座位,有一次报告会恰好坐满了听众,报告会结束后,为了听取意见,需要请32名听众进行座谈.③东方中学共有160名教职工,其中一般教师120名,行政人员16名,后勤人员24名.为了了解教职工对学校在校务公开方面的意见,拟抽取一个容量为20的样本.较为合理的抽样方法是 (A )①简单随机抽样,②系统抽样,③分层抽样. (B )①简单随机抽样,②分层抽样,③系统抽样. (C )①系统抽样,②简单随机抽样,③分层抽样. (D )①分层抽样,②系统抽样,③简单随机抽样.8. 已知函数23,0,(),0,x x f x x x ->⎧=⎨≤⎩ 若)4()(f a f =,则实数a =(A )4(B ) 1或1-(C )1-或4(D )1, 1-或49. 已知)(x f 是定义在R 上的奇函数,且1)1(=f ,若将)(x f 的图象向右平移一个单位后,则得到一个偶函数的图象,则(1)(2)(3)(2009)f f f f ++++=(A )0 (B )1(C )-1(D )-1004.510.已知O 是△ABC 内部一点,OA +OB +OC=0,︒=∠=⋅30BAC ,32且,则AOB∆的面积为(A )2 (B )1 (C )21 (D )31二.填空题:本大题共7小题,每小题4分,共28分. 把答案填在答题卡的相应位置. 11. 已知1z 2i =+,2z 13i =-,则复数21i z z +的虚部为 ▲ . 12. 已知直线l 和两个不同的平面,αβ,则下列命题中错误..的是 ▲ (请写出错误..命题的序号).①若//,//l l αβ,则//αβ ②若,l l αβ⊥⊥,则//αβ ③若,l ααβ⊥⊥,则//l β ④若//,l ααβ⊥,则l β⊥ 13.根据右边程序框图,若输出y 的值是4,则输入的实数x = ▲ .14.已知命题p :21,22≤+∈∃xx R x , 命题q 是命题p 的否定,则命题p 、q 、q p ∧、p q ∨中是真命题的是 ▲ .15.已知双曲线)0,(422≠∈=-a R a a y x 的右焦点是椭圆191622=+y x 的一个顶点,则 a = ▲ .16. 已知向量b a x f x t b x a ⋅===)(),,(),1,(sin 若函数在区间⎪⎭⎫⎝⎛2,0π上是增函数,则实数t 的取值范围是 ▲ .17.有一堆除颜色外其它特征都相同的红白两种颜色的球若干个,已知红球的个数比白球多,但比白球的2倍少,若把每一个白球都记作数值2,每一个红球都记作数值3,则所有球的数值的总和等于60.现从中任取一个球,则取到红球的概率等于 ▲ .三.解答题:本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤. 18.(本题满分14分)在ABC ∆中,c b a ,,是角C B A ,,所对的边,已知02cos 2sin cos 42=+B BB . (Ⅰ)求角B 的大小;(Ⅱ)若ABC a ∆=,4的面积为35,求b 的值.19.(本题满分14分)已知四棱锥P ABCD -中,PA ⊥底面ABCD ,AB ∥CD ,AD =CD 1=,120BAD ︒∠=,PA =90ACB ︒∠=.(Ⅰ)求证:BC ⊥平面PAC ;(Ⅱ)求直线PC 与平面PAB 所成的角的正弦值.20.(本题满分14分)已知数列{}n a 的首项211=a ,前n 项和n n a n S 2=. (Ⅰ)求证:n n a n na 21+=+; (Ⅱ)记n n S b ln =,n T 为{}n b 的前n 项和,求n e nT --的值.21.(本题满分15分)已知定义在R 上的函数),,()(3R c b a c bx ax x f ∈++=,当1-=x 时,)(x f 取得极大值3,1)0(=f . (Ⅰ)求)(x f 的解析式;(Ⅱ)已知实数t 能使函数f (x)(t,t 3)+在区间上既能取到极大值,又能取到极小值,记所有的实数t 组成的集合为M.请判断函数()()()f x g x x M x=∈的零点个数.22.(本题满分15分)已知点(0,)B t ,点(0,4)C t -(其中04t <<),直线PB 、PC都是圆:M 1)1(22=+-y x 的切线.(Ⅰ)若PBC ∆面积等于6,求过点P 的抛物线)0(22>=p px y 的方程; (Ⅱ)若点P 在y 轴右边,求PBC ∆面积的最小值.DCBAPPCB数学(文科)参考答案及评分标准1-10.CDBBA CACBD11.1- 12. ①③④ 13.-2或1 14. p 、q p ∨ 15.2 16. [1,)-+∞ 17.1423.18.解:(1)由已知,01cos 2)cos 1(cos 22=-+-B B B ;3,21cos π==B B 所以得7分 (2)由,535sin 21==c B ac 得 10分 由余弦定理得.21,212154225162==⨯⨯⨯-+=b b 所以14分19.(1)证明:∵PA ⊥底面ABCD ,BC ⊂平面AC ,∴PA ⊥BC,3分 ∵∠ACB=90°,∴BC ⊥AC ,又PA ∩AC=A ,∴BC ⊥平面PAC.5分(2)解:过C 作CE ⊥AB 于E ,连接PE , ∵PA ⊥底面ABCD ,∴CE ⊥面PAB , ∴直线PC 与平面PAB 所成的角为EPC ∠,10分∵AD=CD=1,∠ADC=60°,∴AC=1,PC=2,ACD Rt ∆中求得CE=23,∴43sin =∠EPC .14分20.解:(1)由n n a n S 2=①,得121)1(+++=n n a n S ②,②-①得:n n a n na 21+=+. 4分(2)由n n a n n a 21+=+求得)1(1+=n n a n . 7分∴12+==n na n S n n ,)1ln(ln ln +-==n n Sb n n 11分 (ln1ln 2)(ln 2ln3)(ln3ln 4)(ln ln(1))ln(1)n T n n n =-+-+-++-+=-+∴1)1ln(=-=-+-n e n e n T n .14分21.解:(1)由1)0(=f 得c=11分⎩⎨⎧=+--=-=+=-+=31)1(03)1(,3)('2'b a f b a f b ax x f , 4分得3,1-==b a市一次模文数参答—1(共2页)∴13)(3+-=x x x f5分(2))1)(1(3)('+-=x x x f 得1-=x ,1=x 时取得极值.由)3,(1+∈-t t ,)3,(1+∈t t 得.12-<<-t ∴)1,2(--=M . 8分31)()(2-+==x x x x f x g ,2'12)(xx x g -=,∴当M x ∈时,0)('<x g , ∴)(x g 在M 上递减.12分 又3)1(,21)2(-=-=-g g ∴函数M x xx f x g ∈=,)()(的零点有且仅有1个 15分22.解:(1) 设),(p p y x P ,由已知0>p x ,)6,3(,3,6421p P x x S p p PBC ±∴=∴=⨯⨯=∆ , 2分设直线PB 与圆M 切于点A ,)0,1(M又5,2,61)244(21=∴=∴=⨯++⨯=∆PM PA PA S PBC , ,61,564=∴=+=∴p p PM x 31y 2=∴6分 (2) 点 B (0,t ),点)4,0(-t C ,7分进一步可得两条切线方程为:482158:,21:22-+--+-=+-=t x t t t y PC t x t t y PB ,9分∴4821582122-+--+-=+-t x t t t t x t t p p ,148222+--=∴t t t t x p , 380,40≥<∴<<p p x x t 或 ,38,0≥∴>p p x x ,13分316421≥⨯⨯=∆p PBC x S ,又2=t 时,316=∆PBC S ,∴PBC ∆面积的最小值为31615分。
