方程求根 实验报告
大学数学实验报告----迭代(一)——方程求解

Do M n , n, 2, 100
运行结果:
M n_Integer : Module y, k , m 2; k m ^ n 1 ;
x Mod k, n ;
Print n, " ", PrimeQ n , " ", x, "
", GCD m, n
Do M n , n, 2, 100
2 True 0 2 3 True 1 1 4 False 0 2 5 True 1 1 6 False 2 2 7 True 1 1 8 False 0 2 9 False 4 1 10 False 2 2 11 True 1 1 12 False 8 2 13 True 1 1 14 False 2 2 15 False 4 1 16 False 0 2 17 True 1 1 18 False 14 2 19 True 1 1 20 False 8 2 21 False 4 1 22 False 2 2 23 True 1 1 24 False 8 2 25 False 16 1 26 False 2 2 27 False 13 1 28 False 8 2 29 True 1 1 30 False 2 2 31 True 1 1 32 False 0 2 33 False 4 1 34 False 2 2 35 False 9 1 36 False 32 2 37 True 1 1 38 False 2 2 39 False 4 1 40 False 8 2
99 False 3 27 100 False 1 67 Null2
m=4 时
输入程序:
M n_Integer : Module y, k , m 4; k m ^ n 1 ; x Mod k, n ; Print n, " ", PrimeQ n , " ", GCD m, n , " ", x Do M n , n, 2, 100
数值计算实验报告

本科实验报告课程名称:计算机数值方法实验项目:方程求根、线性方程组的直接解法、线性方程组的迭代解法、代数插值实验地点:专业班级:学生姓名:指导教师:实验一方程求根}五、实验结果与分析二分法实验结果迭代法实验结果结果分析:本题目求根区间为[1,2],精度满足|x*-x n|<0.5×10-5,故二分法用公式|x*-x n|<(b-a)/ 2n,可求得二分次数并输出每次结果。
对迭代法首先要求建立迭代格式。
迭代格式经计算已输入程序之中,故直接给初值便可利用迭代法求出精度下的解。
六、讨论、心得每次的实验都是对已学过的理论知识的一种实战。
通过本次实验,我将二分法与迭代法的思路清晰化并且将其变成计算机设计语言编写出来,运用到了实际解决问题上感觉很好。
我自认为本次跟其他同学比较的优点在于我在二分法实现的时候首先利用换底公式将需要的二分次输输出,如此便很清晰明了的知道接下来每一步的意思。
迭代法给我的感觉便是高度的便捷简化,仅用几行代码便可以同样解决问题。
相比较二分法来说,我更喜欢迭代的思路。
实验二线性方程组的直接解法for(k=n-2;k>=0;k--){sum=0;for(j=k+1;j<n;j++)sum=sum+a[k][j]*x[j];x[k]=(b[k]-sum)/a[k][k];}for(i=0;i<n;i++)printf("x[%d]=%f ",i,x[i]); printf("\n"); //输出解向量x}五、实验结果与分析结果结果分析:如上图所示,输入线性方程组元数n=3,则会要求输入3*3的系数矩阵A与向量b构成的增广矩阵。
根据算法需要将系数矩阵A消元成上三角矩阵。
随后根据矩阵乘法公式变形做对应的回代。
六、讨论、心得本次实验在编写时候感觉还好,感觉将思路变成了程序设计语言,得以实现题目的要求。
但是在运行以及结果分析的时候,感觉到了本实验的一些不足之处:就是我的实验虽然可以实现不同的元数的线性方程组求解,但是缺少了分析初始条件——主元素不能为零。
太原理工大学计算机数值方法实验报告

3.实验完成,提交实验结果并写出报告,分析计算结果是否符合问题的要求,找出计算成功的原因或计算失败的教训。
2、实验内容和原理:
(1)Gauss消元法:基本思想为:对于n阶线性方程组,只要各步主元素不为0,经过n-1步消元,就可以得到一个等价的的系数矩阵为上三角形矩阵的方程组,然后再利用回代过程即可求得原方程的解。时间复杂度约为O(n3)。
return 0;
}
(2)二分法:
#include<stdio.h>
#include<math.h>
#define esp 1e-3 //精度
double f(double x) //原函数
{
return (x*x*x+4*x*x-10);
}
double root(double (*fun)(double),double left,double right,double deviation)//用二分法求方程根
return x0; //满足精度要求时返回Xn+1的值
}
int main()
{
double x0=1.5;//初始近似值
double e=pow(10,-3); //精度
printf("初始近似值为:%lf\n",x0);
printf("近似根为:%lf\n",newton(x0,e));
return 0;
{ //其中形参*fun为指向原函数的指针
double x,y;
while(fabs(right-left)>deviation)//当不满足精度要求继续执行循环体
{
太原理工大学数值计算试验报告

TAIYUAN UNIVEaSIIY OF TECHNOLOGY本科实验报告计算机数值方法课程名称:实验项目:方程求根,线性方程组的直接求解, 线性方程组的迭代求解,代数插值和最小二乘法拟合实验地点:软件楼208 _______________专业班级:学号:学生姓名:___________________________指导教师:李志崔冬华2015年6月5 日实验内容和要求(必填)目的:《数值计算方法》是一门实践性和实用性都很强的课程,学习的目的在于应用已有的理论基础和技术方法,实现对实际计算问题的计算机求解。
本实验配合《计算数值方法》课堂教学,通过上机实践实验环节,巩固课堂和书本上所学的知识、加强实践能力、提高解决实际计算问题的水平、启发创新思想。
其基本目的是:(1)培养理论联系实际的思路,训练综合运用已经学过的理论和实际知识去分析和解决实际问题的能力。
(2)帮助学生全面消化已学的相关课程内容,深刻理解计算数值方法课程的内涵,培养使用电子计算机进行科学计算和解决问题的能力。
(3)进行基本技能训练和巩固。
使学生得到选择算法、编写程序、分析数值结果、写数值试验报告、课堂讨论等环节的综合训练。
要求:(1)应用结构化程序设计编出通用程序,源程序要有详细的注释和说明;(2)比较计算结果,分析数值解误差的原因;(3)实验完成,要求提交实验结果并写出报告,分析计算结果是否符合问题的要求,找出计算成功的原因或计算失败的教训。
实验原理(必填)选择上述方法中的两种方法求方程:f(x)=x3+4x2-10=0在[1,2]内的一个实根,且要求满足精度lx*-x n l<0.5x10-5主要仪器设备笔记本计算机实验记录(写出实验内容中的程序代码和运行结果)(可分栏或加页)迭代法:#include "stdafx.h"#include"stdio.h"#include〃math.h〃#include〃iostream〃using namespace std;float main()(float a;cin>>a;float t, x;x=a;do(x=sqrt((10-x*x*x)/4);t=a;a=x;}while(fabs(a-t)>0.5*1e-5);printf(〃x=%f〃,a); system(〃pause〃);)割线法:#include "stdafx.h"#include〃stdio.h〃#include〃math.h〃#include〃iostream〃using namespace std;float main()(float c,a=1.0,b=2.0;//cin>>a>>b;while(1)(c=b-(b*b*b+4*b*b-10)*(b-a)/(b*b*b+4*b*b-(a*a*a+4*a*a));if (fabs(b-c)<0.5*0.000001) break;b=c;)cout<<c;)实验结果和分析实验结果:心得体会(遇到的问题和解决方法)使用不同的方法,可以不同程度的求得方程的解,不同的方法速度不同。
数学实验报告高中

一、实验目的1. 深入理解数学概念和原理,提高数学思维能力和实践能力。
2. 掌握数学实验的基本方法和步骤,培养科学实验精神。
3. 通过实验验证数学理论,提高数学应用能力。
二、实验内容本次实验以《高中数学实验指导》中的“一元二次方程的解法探究”为例,进行以下实验:1. 实验一:验证一元二次方程的求根公式2. 实验二:探究一元二次方程的根与系数的关系3. 实验三:利用一元二次方程解决实际问题三、实验方法1. 实验一:利用计算机软件(如MATLAB、Mathematica等)或手工计算验证一元二次方程的求根公式。
2. 实验二:通过编程或手工计算,观察一元二次方程的根与系数之间的关系。
3. 实验三:结合实际情境,运用一元二次方程解决实际问题。
四、实验步骤1. 实验一:(1)选择一组一元二次方程,如ax^2 + bx + c = 0(a≠0);(2)利用计算机软件或手工计算,分别求出该方程的两个根;(3)将求得的根代入求根公式,验证其正确性。
2. 实验二:(1)选择一组一元二次方程,如ax^2 + bx + c = 0(a≠0);(2)观察方程的根与系数a、b、c之间的关系;(3)通过编程或手工计算,验证根与系数的关系。
3. 实验三:(1)选择一个实际问题,如:某商品的原价为x元,降价10%后,售价为0.9x元,求原价x;(2)根据实际问题,列出相应的一元二次方程;(3)求解方程,得到原价x;(4)验证求解结果是否满足实际问题。
五、实验结果与分析1. 实验一:通过实验验证,一元二次方程的求根公式在计算机软件或手工计算中均能得出正确结果。
2. 实验二:通过观察和验证,一元二次方程的根与系数之间存在以下关系:(1)当b^2 - 4ac > 0时,方程有两个不相等的实数根;(2)当b^2 - 4ac = 0时,方程有两个相等的实数根;(3)当b^2 - 4ac < 0时,方程无实数根。
3. 实验三:以实际问题为例,设原价为x元,根据题意列出方程0.9x = 100,解得x =100/0.9 ≈ 111.11。
计算方法-方程求根实验
实验四 方程求根实验一. 实验目的(1)深入理解方程求根的迭代法的设计思想,学会利用校正技术和松弛技术解决某些实际的非线性方程问题,比较这些方法解题的不同之处。
(2)熟悉Matlab 编程环境,利用Matlab 解决具体的方程求根问题。
二. 实验要求用Matlab 软件实现根的二分搜索、迭代法、Newton 法、快速弦截法和弦截法,并用实例在计算机上计算。
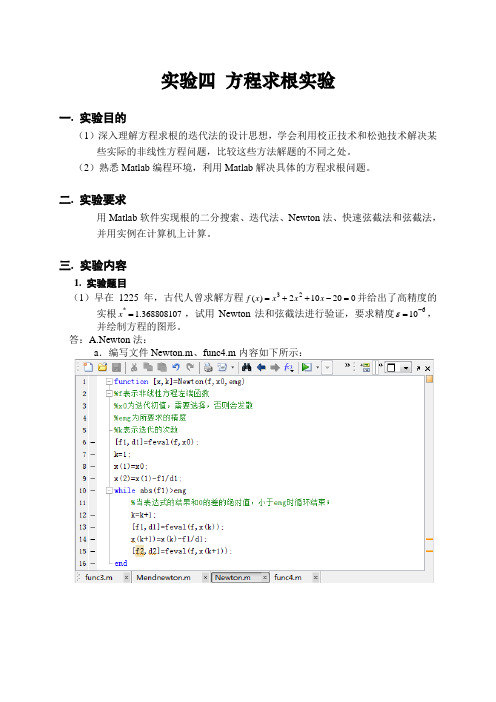
三. 实验内容1. 实验题目(1)早在1225年,古代人曾求解方程020102)(23=-++=x x x x f 并给出了高精度的实根368808107.1*=x ,试用Newton 法和弦截法进行验证,要求精度610-=ε,并绘制方程的图形。
答:A.Newton 法:a .编写文件Newton.m 、func4.m 内容如下所示:b.运行,如下所示A为矩阵,由上面可知,对于初值为5,运行7次即可得到所需的精度,验证结果为古人给出的解释正确的;c.作图,编写下面的文件photo1.m.然后运行即可:注意下面中的x矩阵即为刚才计算出来的x系列,k为迭代的次数:a.编写文件Chord.m内容如下所示:b.运行结果如下所示:由上表可知,在精度为10^-6时有7位有效数字,古人的结果还是正确的c.作图,在上面运行后,即运行newton法时写的photo1.m文件即可出现图像:可以看到图中两条曲线基本重合; (2)取5.00=x ,用迭代法求方程x e x -=的根,然后用Aitken 方法加速,要求精度为结果有4为有效数字。
答:a. 编写文件func7.m 和Aiken.m ,内容如下所示:b .运行:具有四位有效数字 (3)用快速弦截法求解方程01)(=-=x xe x f ,要求精度为610-=ε,取6.05.010==x x ,作为开始值,并绘制1)(-=x xe x f 的图形。
答:对照可知,书本后面的程序已经正确,运行即可:下面为快速弦截法的主程序文件:函数文件如下:运行如下:作图,编写下面的文件:运行该文件就可以y=x*exp(x)-1函数和插值函数的图:可以看到两条直线基本重合在一起了,扩大图片可以看到两条直线是不重合的:2. 设计思想要求针对上述题目,详细分析每种算法的设计思想。
实验一 非线性方程求根

计算方法课程实验报告实验名称 非线性方程求根班级 动创新13 姓名 封敏丽 学号 201302400104序号 教师赵美玲 地点数学实验中心评分一、 实验目的① 掌握二分法、牛顿迭代法等常用的非线性方程迭代算法; ② 了解迭代算法的设计原理及初值对收敛性的影响。
二、用文字或图表记录实验过程和结果题目求方程32()330f x x x x =+--=在1.5 附近的根.(误差限为16,19e e εη=-=-)(1)编程实现二分法,并求解上述非线性方程的根(有根区间自己确定)。
(2)设计弦截法,计算原方程的根。
参考答案原方程的根为 1.732051x = (1)有根区间取[1.5 2];用Matlab 进行运算,先编写程序如下: f=input('输入函数f(x)='); qujian=input('输入区间='); err=input('输入误差='); a=qujian(1); b=qujian(2); yc=1;k=0;%计二分法的次数 while ((b-a)>err&yc~=0); c=(a+b)/2; x=a;ya=eval(f); x=b;yb=eval(f); x=c;yc=eval(f); if ya*yc<0 b=c; else a=c; endx0=c;k=k+1;end将以上程序保存为文件erfenfa.m。
调用erfenfa得到如下结果:这个时候将在Workspace区域得到x0和k的值如下:如上图所示,用二分法得到方程的近似根约为1.732051,二分次数为19.二分法流程图如下:YNN YNY开始输入a ,b ,c X0=1/2(a+b) F(a)=x*x*x+x*x-3x-3 F(x0)=x0*x0*x0+x0*x0-3x0-3 F(x0)=0F(a)F(x0))<0a=x0 b=x0 │a-b │<c 输出x0 结束(2)有根区间取(1.5,2)用Matlab编程,代码如下:先建立一个m文件:function y=f(t)y=t^3+t^2-3*t-3;以bangf.m为文件名保存,然后新建一个m文件:i=0;%迭代次数t1=1.5;%迭代初始值1t2=2;%迭代初始值2while i<=100;y=t2-bangf(t2)/(bangf(t2)-bangf(t1))*(t2-t1);%弦截法迭代格式if abs(y-t2)>10^(-6); %收敛判据t1=t2;t2=y;else breakendi=i+1;endfprintf('\n%s%.6f\t\t%s%d%','待求根x=',y,'迭代次数i=',i) ;%输出结果最后将在工作区显示结果如下:所以得到方程的近似根约为1.732051,迭代次数为4.弦截法流程图如下:│YNYNNY开始 定义f (x ),g (x )以及输入x0,e1,e2,N k=k+1 f (x0)<e1x1=x0-f(x0)/g(x0) │x1-x0│<e2k=N? 输出迭代失败标志结束输出x1 输出奇异标志 x0=x1 K=k+1三、练习与思考题分析解答① 比较二分法和牛顿法在非线性方程求根中的优缺点和收敛速度。
数值分析实验报告——非线性方程求根

数值分析实验报告——非线性方程求根二分法一、题目用二分法求方程=的所有根x.13要求每个根的误差小于-x+0.001..21二、方法二分法三、程序1、Jiangerfen.M的程序function[c,yc]=jiangerfen(f,a,b,tol1,tol2)if nargin<4 tol1=1e-3;tol2=1e-3;end%nargin<4表示若赋的值个数小于4,则tol1和tol2取默认值。
ya=feval('f',a);%令x=a代入到方程f中,ya即f(a)。
yb=feval('f',b);if ya*yb>0,disp('(a,b)不是有根区间');return,endmax=1+round((log(b -a)-log(tol2))/log(2));%round函数是将数据取整,使数据等于其最接近的整数。
for k=1:maxc=(a+b)/2;yc=feval('f',c);if((b-a)/2<tol2)|(abs(yc)<tol1),break,endif yb*yc<0a=c;ya=yc;elseb=c;yb=yc;endendk,c=(a+b)/2,yc=feval('f',c)2、f.M的程序function y=f(x);y=x^3-2*x-1;四、结果>> format compact>> fplot('[x^3-2*x-1,0]',[-1.5,2]);>> jiangerfen('f',-1.5,-0.8);k =8c =-0.9996yc =3.9017e-004>> jiangerfen('f',-0.8,-0.3);k =8c =-0.6184yc =2.7772e-004>> jiangerfen('f',1.3,2);k =10c =1.6179yc =-9.5348e-004>> jiangerfen('f',2,3);(a,b)不是有根区间方程f(x)=x^3-2*x-1的所有根为-0.9996,-0.6184 ,1.6179 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一方程求根
一、实验目的
用各种方法求任意实函数方程f(x)=0在自变量区间[a,b]上,或某一点附近的实根。
并比较方法的优劣。
二、实验方法
(1)二分法
对方程f(x)=0在[a,b]内求根。
将所给区间等分,在分点x=(b-a)/2判断是否f(x)=0,若是,则有根x=(b-a)/2.否则,继续判断是否f(a)·f(x)<0,若是,则令b=x,否则令a=x。
重复此过程直至求出方程f(x)=0在[a,b]中的近似根为止。
(2)迭代法
将方程f(x)=0等价变换为x=h(x)形式,并建立相应的迭代公式Xk+1=h(Xk)。
(3)牛顿法
若已知方程f(X)=0的一个近似根X0,则函数f(X)在点X0附近可用一阶泰勒多项式P1= f (X0) + f’ (X0) (X-X0)来近似,因此方程f(X)=0可近似表示为f(X0)+ f’ (X0) (X-X0)=0.设f’ (X0)≠0,则X= X0- f (X0)/ f’ (X0),取X作为原方程新的近似根X1,然后将X1作为X0带入上式,迭代公示为:X k+1=X k - f (X k)/ f’ (X k)。
三、实验内容
在区间[0,1]上用二分法求方程的近似根,要求误差不超过0.5×10^3。
取初值X0=0,用迭代公式X k+1=(2-e^k)/10,(k=0,1,2,…)求方程e^x+10x-2=0的近似根。
要求误差不超过0.5×10^3。
取初值X0=0,用牛顿迭代法求方程e^x+10x-2=0的近似根。
要求误差不超过0.5×10^3。
四、实验程序
1.二分法
function x=agui_bisect(fname,a,b,e)
fa=feval(fname,a);
fb=feval(fname,b);
if fa*fb>0 error('两端函数值为同号');end
k=0
x=(a+b)/2
while(b-a)>(2*e)
fx=feval(fname,x);
if fa*fx<0
b=x;
fb=fx;
else
a=x;
fa=fx;
end
k=k+1
x=(a+b)/2
end
2.迭代法
function x=agui_iterative(fname,x0,e)
N=100;
x=x0;
x0=x+2*e;
k=0;
while abs(x0-x)>e & k<N
k=k+1
x0=x;
x=feval(fname,x0);
disp(x)
end
if k==N warning('已达最大迭代次数');
end
3.牛顿法
function x=agui_newton(fname,dfname,x0,e)
N=100;
x=x0;
x0=x+2*e;
k=0;
while abs(x0-x)>e&k<N
k=k+1
x0=x;
x=x0-feval(fname,x0)/feval(dfname,x0);
disp(x)
end
if k==N warning('已达最大迭代次数');end
五、实验结果
1.二分法
2.迭代法
3.牛顿法
六、结果分析
二分法要循环10次,迭代法要迭代4次,牛顿法要迭代3次才能达到精度为0.5×1^-3的要求,由此可知:
二分法方法简单,编程容易,且对函数f(x)的性质要求不高,但其收缩速度较慢,计算量大,因此常被用于精度不高的近似根,或为迭代法求初值。
迭代法原理简单,计算量相对二分法较小,但存在收敛性和收敛速度的问题。
牛顿法是一种特殊的迭代法,不仅计算量少而且精确度高,对初值的选取要求苛刻,且需要求函数的重根。
各种方法各有优劣,因此我们应根据不同的函数具体分析,达到最优化。
