向量加减混合运算-高中数学知识点讲解(含答案)
高中数学必修二第六章平面向量及其应用重点知识点大全(带答案)

高中数学必修二第六章平面向量及其应用重点知识点大全单选题1、若M 为△ABC 的边AB 上一点,且AB⃑⃑⃑⃑⃑ =3AM ⃑⃑⃑⃑⃑⃑ ,则CB ⃑⃑⃑⃑⃑ =( ) A .3CM⃑⃑⃑⃑⃑⃑ −2CA ⃑⃑⃑⃑⃑ B .3CA ⃑⃑⃑⃑⃑ −2CM ⃑⃑⃑⃑⃑⃑ C .3CM ⃑⃑⃑⃑⃑⃑ +2CA ⃑⃑⃑⃑⃑ D .3CA ⃑⃑⃑⃑⃑ +2CM ⃑⃑⃑⃑⃑⃑ 答案:A解析:先用向量CB →,CA →表示向量CM →,再转化为用CA →,CM →表示CB →即可得答案.解:根据题意做出图形,如图,所以CM →=CB →+BM →=CB →+23BA →=CB →+23(CA →−CB →)=13CB →+23CA →,所以CB →= 3CM →−2CA →.故选:A.小提示:关键点睛:解题关键在于利用向量的线性运算进行求解,属于基础题2、已知向量a ,b ⃑ 满足|a |⃑⃑⃑⃑⃑ =1,a ⊥b ⃑ ,则向量a −2b ⃑ 在向量a 方向上的投影向量为( )A .aB .1C .-1D .−a答案:A分析:根据给定条件,求出(a −2b ⃑ )⋅a ,再借助投影向量的意义计算作答.因|a |⃑⃑⃑⃑⃑ =1,a ⊥b ⃑ ,则(a −2b ⃑ )⋅a =a 2−2b ⃑ ⋅a =1,令向量a −2b ⃑ 与向量a 的夹角为θ,于是得|a −2b ⃑ |cosθ⋅a ⃑ |a ⃑ |=(a ⃑ −2b ⃑ )⋅a ⃑ |a ⃑ |⋅a⃑ |a ⃑ |=a ,所以向量a −2b ⃑ 在向量a 方向上的投影向量为a .故选:A3、如图,四边形ABCD 是平行四边形,则12AC ⃑⃑⃑⃑⃑ +12BD ⃑⃑⃑⃑⃑⃑ =( )A .AB ⃑⃑⃑⃑⃑ B .CD ⃑⃑⃑⃑⃑C .CB ⃑⃑⃑⃑⃑D .AD ⃑⃑⃑⃑⃑答案:D分析:由平面向量的加减法法则进行计算.由题意得AC ⃑⃑⃑⃑⃑ =AB ⃑⃑⃑⃑⃑ +AD ⃑⃑⃑⃑⃑ ,BD ⃑⃑⃑⃑⃑⃑ =AD ⃑⃑⃑⃑⃑ −AB ⃑⃑⃑⃑⃑ ,所以12AC ⃑⃑⃑⃑⃑ +12BD ⃑⃑⃑⃑⃑⃑ =12(AB ⃑⃑⃑⃑⃑ +AD ⃑⃑⃑⃑⃑ +AD ⃑⃑⃑⃑⃑ −AB ⃑⃑⃑⃑⃑ )=AD ⃑⃑⃑⃑⃑ .故选:D.4、下列条件中能得到a ⃗=b ⃑⃗的是( )A .|a ⃗|=|b ⃑⃗|B .a ⃗与b ⃑⃗的方向相同;C .a ⃗=0⃑⃗,b ⃑⃗为任意向量D .a ⃗=0⃑⃗且b ⃑⃗=0⃑⃗答案:D分析:根据相等向量的概念,即可得到结果.由于a ⃗=b ⃑⃗,所以a ⃗与b ⃑⃗的大小相等,方向相同,故D 正确.故选:D.5、向量a ⃗,b ⃑⃗满足a ⃗=(1,√3),|b ⃑⃗|=1,|a ⃗+b ⃑⃗|=√3,则b ⃑⃗在a ⃗方向上的投影为()A .-1B .−12C .12D .1答案:B解析:根据题条件,先求出a ⃗⋅b ⃑⃗,再由向量数量积的几何意义,即可求出结果.因为向量a ⃗,b ⃑⃗满足a ⃗=(1,√3),|b ⃑⃗|=1,|a ⃗+b ⃑⃗|=√3,所以|a ⃗|2+2a ⃗⋅b ⃑⃗+|b ⃑⃗|2=3,即4+2a ⃗⋅b ⃑⃗+1=3,则a ⃗⋅b⃑⃗=−1, 所以b ⃑⃗在a ⃗方向上的投影为|b →|cos <a →,b →>=a →⋅b →|a →|=−12. 故选:B.6、在△ABC 中,内角A,B,C 的对边分别为a,b,c ,且a (sin A −sin B )+b sin B =c sin C,a +b =2c =2,则△ABC 的面积为( )A .3√38B .√34C .√32D .3√32 答案:B分析:由正弦定理化角为边结合余弦定理可求出C =π3,再由已知可求出ab =1,即可求出面积.因为a (sin A −sin B )+b sin B =c sin C ,由正弦定理得a (a −b )+b 2=c 2,即a 2+b 2−c 2=ab ,所以cos C =a 2+b 2−c 22ab =12, 又C ∈(0,π),所以C =π3.又a +b =2c =2,则c =1,a +b =2,由a 2+b 2−c 2=a 2+b 2−1= ab,(a +b)2−3ab =1,得ab =1.所以S △ABC =12ab sin C =12×1×1×sin π3=√34. 故选:B.7、在△ABC 中,已知b 2=ac 且c =2a ,则cos B 等于( )A .14B .34C .√24D .√23答案:B分析:利用余弦定理求得cosB .b 2=ac,c =2a ,则b 2=2a 2,由余弦定理得cosB =a 2+c 2−b 22ac =a 2+4a 2−2a 22a⋅2a =34. 故选:B8、在△ABC 中,若AB⃑⃑⃑⃑⃑ ⋅BC ⃑⃑⃑⃑⃑ +AB ⃑⃑⃑⃑⃑ 2=0,则△ABC 的形状一定是( ) A .等边三角形B .直角三角形C .等腰三角形D .等腰直角三角形答案:B分析:先利用数量积运算化简得到accosB =c 2,再利用余弦定理化简得解.因为AB ⃑⃑⃑⃑⃑ ⋅BC ⃑⃑⃑⃑⃑ +AB⃑⃑⃑⃑⃑ 2=0,所以accos(π−B)+c 2=0, 所以accosB =c 2,所以ac ×a 2+c 2−b 22ac =c 2,所以b 2+c 2=a 2,所以三角形是直角三角形.故选:B多选题9、下列结果为零向量的是( )A .AB ⃑⃑⃑⃑⃑ −(BC ⃑⃑⃑⃑⃑ +CA ⃑⃑⃑⃑⃑ )B .AB ⃑⃑⃑⃑⃑ −AC ⃑⃑⃑⃑⃑ +BD⃑⃑⃑⃑⃑⃑ −CD ⃑⃑⃑⃑⃑ C .OA ⃑⃑⃑⃑⃑ −OD ⃑⃑⃑⃑⃑⃑ +AD ⃑⃑⃑⃑⃑ D .NO ⃑⃑⃑⃑⃑⃑ +OP ⃑⃑⃑⃑⃑ +MN ⃑⃑⃑⃑⃑⃑⃑ −MP⃑⃑⃑⃑⃑⃑ 答案:BCD分析:根据向量加减法的运算方法即可逐项判断.A 项,AB⃑⃑⃑⃑⃑⃗−(BC ⃑⃑⃑⃑⃑⃗+CA ⃑⃑⃑⃑⃑⃗)=AB ⃑⃑⃑⃑⃑⃗−BA ⃑⃑⃑⃑⃑⃗=2AB ⃑⃑⃑⃑⃑⃗; B 项,AB ⃑⃑⃑⃑⃑⃗−AC ⃑⃑⃑⃑⃑⃗+BD ⃑⃑⃑⃑⃑⃑⃗−CD ⃑⃑⃑⃑⃑⃗=CB ⃑⃑⃑⃑⃑⃗+BC ⃑⃑⃑⃑⃑⃗=0⃑⃗;C 项,OA ⃑⃑⃑⃑⃑⃗−OD ⃑⃑⃑⃑⃑⃑⃗+AD ⃑⃑⃑⃑⃑⃗=DA ⃑⃑⃑⃑⃑⃗+AD ⃑⃑⃑⃑⃑⃗=0⃑⃗;D 项,NO ⃑⃑⃑⃑⃑⃑⃗+OP ⃑⃑⃑⃑⃑⃗+MN ⃑⃑⃑⃑⃑⃑⃑⃗−MP ⃑⃑⃑⃑⃑⃑⃗=NP ⃑⃑⃑⃑⃑⃑⃗+PN ⃑⃑⃑⃑⃑⃑⃗=0⃑⃗.故选:BCD.10、已知向量a ⃗=(1,−2),b⃑⃗=(−1,m),则( ) A .若a ⃗与b ⃑⃗垂直,则m =−1B .若a ⃗//b⃑⃗,则m =2 C .若m =1,则|a ⃗−b ⃑⃗|=√13D .若m =−2,则a ⃗与b⃑⃗的夹角为60° 答案:BC分析:利用向量垂直、平行的坐标表示求参数m ,即可判断A 、B 的正误;由m 的值写出b⃑⃗的坐标,再由向量坐标的线性运算及模长的坐标求法、夹角的坐标求法求|a ⃗−b ⃑⃗|、a ⃗与b⃑⃗的夹角,即可判断C 、D 正误. A :a ⃗与b ⃑⃗垂直,则−1−2m =0,可得m =−12,故错误;B:a⃗//b⃑⃗,则m−2=0,可得m=2,故正确;C:m=1有b⃑⃗=(−1,1),则a⃗−b⃑⃗=(2,−3),可得|a⃗−b⃑⃗|=√13,故正确;D:m=−2时,有b⃑⃗=(−1,−2),所以cos<a⃗,b⃑⃗>=a⃑⃗⋅b⃑⃗|a⃑⃗||b⃑⃗|=√5×√5=35,即a⃗与b⃑⃗的夹角不为60°,故错误.故选:BC11、(多选)已知向量a⃗,b⃑⃗,在下列命题中正确的是()A.若|a⃗|>|b⃑⃗|,则a⃗>b⃑⃗B.若|a⃗|=|b⃑⃗|,则a⃗=b⃑⃗C.若a⃗=b⃑⃗,则a⃗//b⃑⃗D.若|a⃗|=0,则a⃗=0答案:CD分析:根据向量相等和模值相等的区别分析四个选项便可得出答案.解:向量的模值可以比较大小,但是向量不能比较大小,故A错;向量的模值相等,只能证明大小相等并不能说明方向也相同,故B错;两个向量相等,这两个向量平行,所以C正确;模值为零的向量为零向量,故D正确故选:CD填空题12、《后汉书·张衡传》:“阳嘉元年,复造候风地动仪.以精铜铸成,员径八尺,合盖隆起,形似酒尊,饰以篆文山龟鸟兽之形.中有都柱,傍行八道,施关发机.外有八龙,首衔铜丸,下有蟾蜍,张口承之.其牙机巧制,皆隐在尊中,覆盖周密无际.如有地动,尊则振龙,机发吐丸,而蟾蜍衔之.振声激扬,伺者因此觉知.虽一龙发机,而七首不动,寻其方面,乃知震之所在.验之以事,合契若神.”如图,为张衡地动仪的结构图,现要在相距200km的A,B两地各放置一个地动仪,B在A的东偏北60°方向,若A地动仪正东方向的铜丸落下,B地东南方向的铜丸落下,则地震的位置在A地正东________________km.答案:100(√3+1)分析:依题意画出图象,即可得到A=60∘,B=75∘,C=45∘,AB=200,再利用正弦定理计算可得;解:如图,设震源在C处,则AB=200km,则由题意可得A=60∘,B=75∘,C=45∘,根据正弦定理可得200 sin45∘=ACsin75∘,又sin75∘=sin(45∘+30∘)=sin45∘cos30∘+cos45∘sin30∘=√22×√32+√22×12=√6+√24所以AC=200sin75∘sin45∘=200×√6+√24√22=100(√3+1),所以震源在A地正东100(√3+1)km处.所以答案是:100(√3+1)13、已知向量a⃗,b⃑⃗的夹角为120°,|a⃗|=2,|b⃑⃗|=1,若(a⃗+3b⃑⃗)⊥(2a⃗+λb⃑⃗),则实数λ=___________. 答案:−1分析:由(a⃗+3b⃑⃗)⊥(2a⃗+λb⃑⃗),可得(a⃗+3b⃑⃗)⋅(2a⃗+λb⃑⃗)=0,化简后结已知条件可求得答案解:因为向量a⃗,b⃑⃗的夹角为120°,|a⃗|=2,|b⃑⃗|=1,且(a⃗+3b⃑⃗)⊥(2a⃗+λb⃑⃗),所以(a ⃗+3b ⃑⃗)⋅(2a ⃗+λb ⃑⃗)=0,即2a ⃗2+(6+λ)a ⃗⋅b⃑⃗+3λb ⃑⃗2=0, 所以8+(6+λ)×2×1×(−12)+3λ=0,解得λ=−1,所以答案是:−114、设向量m ⃑⃑ =2a −3b ⃑ ,n ⃑ =4a −2b ⃑ ,p =3a +2b ⃑ ,若用m ⃑⃑ ,n ⃑ 表示p ,则p =________.答案:−74m ⃑⃑ +138n ⃑分析:根据平面向量基本定理进行求解即可.设p ⃗=xm ⃑⃑⃗+yn ⃑⃗,则有p ⃗=3a ⃗+2b ⃑⃗=x(2a ⃗−3b ⃑⃗)+y(4a ⃗−2b ⃑⃗)=(2x +4y)a ⃗+(−3x −2y)b⃑⃗, 得{2x +4y =3−3x −2y =2⇒{x =−74,y =138.,所以p ⃗=−74m ⃑⃑⃗+138n ⃑⃗, 所以答案是:−74m ⃑⃑⃗+138n ⃑⃗解答题 15、△ABC 的内角A,B,C 的对边分别为a,b,c ,已知asinAsinB +ccosA =(acosA +2b )cosB(1)求B ;(2)若b =2√3,AB⃑⃑⃑⃑⃑ ⋅CB ⃑⃑⃑⃑⃑ =6,求△ABC 的周长 答案:(1)B =π3;(2)6√3. 分析:(1)根据asinAsinB +ccosA =(acosA +2b )cosB ,利用正弦定理结合两角和与差的三角函数化简为2sinBcosB =sinB 求解;(2)利用余弦定理得到(a +c )2−3ac =12,然后由AB⃑⃑⃑⃑⃑ ⋅CB ⃑⃑⃑⃑⃑ =6求得ac 代入即可. (1)因为 asinAsinB +ccosA =(acosA +2b )cosB ,所以a (sinAsinB −cosAcosB )+ccosA =2bcosB ,所以−acos(A +B)+ccosA =2bcosB所以acosC +ccosA =2bcosB由正弦定理得sinAcosC +sinCcosA =2sinBcosB整理得sin (A +C )=2sinBcosB =sinB因为在△ABC 中,所以sinB ≠0,则2cosB =1所以B =π3 (2)由余弦定理得b 2=a 2+c 2−2accosB ,即(a +c )2−3ac =12,因为AB ⃑⃑⃑⃑⃑ ⋅CB ⃑⃑⃑⃑⃑ =BA ⃑⃑⃑⃑⃑ ⋅BC ⃑⃑⃑⃑⃑ =accosB =12ac =6, 所以ac =12,所以(a +c )2−36=12,解得a +c =4√3.所以△ABC 的周长是6√3小提示:方法点睛:在解有关三角形的题目时,要有意识地考虑用哪个定理更适合,或是两个定理都要用,要抓住能够利用某个定理的信息,一般地,如果式子中含有角的余弦或边的二次式,要考虑用余弦定理;如果遇到的式子中含有角的正弦或边的一次式时,则考虑用正弦定理;以上特征都不明显时,则要考虑两个定理都有可能用到.。
10高中数学“平面向量加减运算与坐标表示”知识点全解析

高中数学“平面向量加减运算与坐标表示”知识点全解析一、引言平面向量的加减运算与坐标表示是向量运算的基础,对于理解向量的本质和性质,以及解决向量相关问题具有重要意义。
本文将详细解析“平面向量加减运算与坐标表示”相关知识点,帮助同学们更好地掌握这一内容。
二、平面向量的加减运算1.向量加法:向量的加法遵循平行四边形法则或三角形法则。
设有两个向量a和b,则它们的和a + b可以表示为第三个向量,这个向量从a的起点指向b的终点,或者通过平移使a和b的起点重合,然后以a和b为邻边作平行四边形,则a + b是与a、b共起点的平行四边形的对角线。
1.向量减法:向量的减法可以看作是加上一个反向的向量。
设有两个向量a和b,则它们的差a - b可以表示为第三个向量,这个向量从b的终点指向a的终点,或者通过平移使a和b的起点重合,然后以b为起点、a为终点的向量即为a - b。
三、平面向量的坐标表示在平面直角坐标系中,我们可以将向量的起点放在坐标原点,用向量的终点坐标来表示这个向量。
设向量a的终点坐标为(x, y),则我们可以将向量a表示为坐标形式(x, y)。
这种表示方法称为向量的坐标表示法。
四、平面向量加减运算的坐标表示1.向量加法的坐标表示:设有两个向量a = (x1, y1)和b = (x2, y2),则它们的和a + b可以表示为坐标形式(x1 + x2, y1 + y2)。
即向量的加法在坐标表示下就是对应坐标分量的加法。
1.向量减法的坐标表示:同样地,设有两个向量a = (x1, y1)和b = (x2, y2),则它们的差a - b可以表示为坐标形式(x1 - x2, y1 - y2)。
即向量的减法在坐标表示下就是对应坐标分量的减法。
五、应用举例1.力的合成与分解:在物理学中,力是矢量,可以用向量来表示。
通过向量的加减运算可以方便地求解多个力的合成或分解问题。
例如求解两个力的合力时可以将这两个力表示为向量然后利用向量的加法运算求得合力的大小和方向。
(整理)高一数学向量的加减法

[教材优化全析]1.向量的加法 (1)引入①某人从A 到B ,再从B 按原方向到C ,则两次的位移和:+BC =AC . A B C②若上题改为从A 到B ,再从B 按反方向到C ,则两次的位移和:AB +BC =AC .③某车从A 到B ,再从B 改变方向到C ,则两次的位移和:AC +BC =AC . A BC上述①②③三个小题,说明向量共线、不共线时都可依据向量的运算法则求“和”.(2)向量的加法的定义 已知向量a 、b ,在平面内任取一点A ,作=a ,=b ,则向量叫做向量a 、b 的和.记作a +b ,即a +b =+BC =AC .求两个向量和的运算,叫做向量的加法.对于零向量与任意向量a ,有a +0=0+a =a .(3)两个向量的和向量的作法如图(1)、(2)、(3)中,=a ,BC =b ,则+BC =AC.(1)(2)(3)A C①三角形法则:上面的(1)、(2)、(3)中各有两个向量,把其中一个向量的起点平移,使之与第二个向量的终点重合,则第一个向量的起点指向第二个向量终点的向量,就是两个向量的和向量.常说两个向量“首尾相接”. 1°三角形法则对于两个向量共线时也适用. 2°可将向量加法的三角形法则推广到多个向量相加的多边形法则. 3°任何一个向量均可以写成两个任意向量之和,只要注意到这个向量的全析提示向量运算是运用向量方法解决问题的基本工具,而向量的加法运算是最基本的向量运算之一,向量加法的平行四边形法则与三角形法则和物理中力的合成、速度的合成完全一致.思维拓展两个向量的和仍是一个向量,这如同两个力的合力仍是力(向量)一样.全析提示向量有几何表示法和字母表示法两种情况.用几何法表示时,箭头所指的方向是正方向;用字母表示时,起点字母在前,终点字母在后,方向由起点指向终点.思维拓展 向量是既有大小又有方向的量,向量的模与方向可通过解三角形的知识求得;对于首尾相连的几个向量的和,等于以第一个向量的起点为起点,第n 个向量的终点为终点的向量.起点、终点即可,如:=+,如下所示,O点具有任意性.AB O课本99页例1.求a+b,在平面内任取一点O,平移a、b使之首尾相接,求和向量.实际上我们常在其中a或b上取一点,只平移一个向量即可.如可把a 的起点移至b的终点可求和向量.②平行四边形法则由同一点A为起点的两个已知向量a、b为邻边作平行四边形ABCD,则以A为起点的对角线就是a与b的和.这种作两个向量和的方法叫做平行四边形法则.不能.因为不可能以两平行向量为邻边作平行四边形.所以,平行四边形法则对于两个向量共线时不适用.(3)两向量的和向量与原向量之间的关系(方向与模).①当向量a、b不共线时,a+b的方向与a、b不同向,且|a+b|<|a|+|b|.②当向量a、b同向时,a+b的方向与a、b同向,且|a+b|=|a|+|b|.当向量a、b反向时,若|a|>|b|,则a+b的方向与a同向,且|a+b|=|a|-|b|.若|a|<|b|,则a+b的方向与a反向,且|a+b|=|b|-|a|.(4)向量的运算律①交换律:a+b=b+a.证明:当向量a、b不共线时如下图,作平行四边形ABCD,使=a,=b,则BC=b,DC=a.全析提示不管平面内的点O选在何处,对于首尾相连的两个和向量,它的方向总是由第一向量的起点指向第二向量的终点.要点提炼在几何中向量的加法是用几何作图来定义的.它有两种法则,其中三角形法则比平行四边形法则更具有一般性.像两个向量共线时就只能用三角形法则了.全析提示当向量a、b不共线时,|a|、|b|及|a+b|构成一个三角形的三条边,由三角形的性质可知:||a|-|b||<|a+b|<|a|+|b|;当向量a、b共线时,|a|、|b|及|a+b|可理解成同一直线上的线段相加减.要点提炼向量的加法同实数的加法一样,满足交换律与结合律.因为=+=a+b,=+=b+a,所以a+b=b+a.当向量a、b共线时,若a与b同向,由向量加法的定义知:a+b与a同向,且|a+b|=|a|+|b|,b+a与a同向,且|b+a|=|b|+|a|,所以a+b=b+a;若a与b反向,不妨设|a|>|b|,同样由向量加法的定义知:a+b与a同向,且|a+b|=|a|-|b|,b+a与a同向,且|b+a|=|a|-|b|,所以a+b=b+a.综上所述,a+b=b+a.②结合律,自己验证一下.由于向量的加法满足交换律和结合律,对于多个向量的加法运算就可以按照任意的次序与任意的组合来进行了.例如化简:(+)+=(+)+=+=.又如化简:CM+(BC+)=(CM+)+BC=CB+BC=0,也可写成CM+(MB+BC)=CM+MC=0.2.向量的减法(1)相反向量:与a长度相等、方向相反的向量叫做相反向量,记作:-a.①规定:零向量的相反向量仍是零向量.②a与-a互为相反向量,即-(-a)=a.③任意向量与它的相反向量的和是零向量,即a+(-a)=(-a)+a=0.又如:与互为相反向量,+=0.④如果a、b互为相反向量,那么a=-b,b=-a,a+b=0.(2)向量减法的定义向量a加上b的相反向量,叫做a与b的差,即a-b=a+(-b).求两个向量的差的运算叫做向量的减法,向量的减法是向量加法的逆运算.若b+x=a,则x叫做a与b的差,记作a-b.(3)a-b的作法由(a-b)+b=a+(-b)+b=a+0=a.所以a-b就是这样一个向量,它与b的和等于a.①已知a、b,怎样求作a-b?解法一:已知向量a、b,在平面内任取一点O,作=a,=b,则=a -b,即a-b可以表示为从向量b的终点指向向量a的终点的向量.思维拓展当向量a与b共线时,求a与b 的和,不管是b以a的终点为起点,还是a以b的终点为起点,它们的和都是从第一个向量的起点指向第二个向量的终点,从图象上看都是相等的.要点提炼由于向量可用表示它的有向线段的起点和终点的字母来表示,根据向量加法的三角形法则,可把首尾相连的向量先结合在一起相加.全析提示向量的减法与加法互为逆运算,有关向量的减法可同加法相类比,也可同实数的减法相类比.全析提示两个向量的差同两个向量的和一样,其运算结果仍是一个向量,它的模与方向可通过解三角形知识求得.全析提示由于向量是以OB的终点为起点的向量,所以根据向量加法的三角形法则有=+,即a+(aA解法二:在平面内任取一点O ,作=a ,=b ,则=a -b , 即a -b 也可以表示为从向量a 的起点指向向量b 的起点的向量.解法三:在平面内任取一点O ,作OA =a ,OB =-b ,则由向量加法的平行四边形法则可得 OC =a +(-b )=a -b .②如下图,若a 与b 共线时,怎样作a -b ?(1)(2)在平面内任取一点O,作=a ,=b .则为所求的向量a -b .(1)(2)B一般地,不论两向量共线还是不共线,常选取一个适当的点,通过平移把两向量的起点重合,则由减数向量的终点指向被减数向量的终点的向量,即为所求的差向量.平行四边形ABCD 中,若设=a ,=b ,则两条对角线都可以用a 与b 表示,借助这一模型可进一步研究有关ABCD的一些性质.如课本103页例4.AC =a +b ,DB =a -b .变式训练一:当a 、b b 垂直?-b )=b .显然减法是加法的逆运算.思维拓展向量a -b =a +(-b ),即向量的减法可用向量加法的三角形法则或平行四边形法则来表示,是化生为熟,化未知为已知的化归思想的具体应用.要点提炼若向量a 、b 是共线向量,则a ±b 与a 、b 仍是共线向量.全析提示从同一点出发的两个不共线向量的和、差同两个向量一起恰好构成一个平行四边形的边与对角线.变式训练二:当a、b满足什么条件时,|a+b|=|a-b|?变式训练三:a+b与a-b可能是相等向量吗?变式训练四:当a与b满足什么条件时,a+b平分a与b所夹的角?答案:一、|a|=|b|,即ABCD为菱形,对角线互相垂直.二、|a+b|=|a-b|,即ABCD 的对角线长相等,ABCD应为矩形,所以应满足a与b垂直.三、a+b与a-b 不可能相等,因为ABCD的方向不同.四、当|a|=|b|时,对角线平分a与b所夹的角.全析提示以平行四边形为起点,借助平面几何图形的性质解答上述问题.。
高中数学必修二第六章平面向量及其应用知识点归纳超级精简版(带答案)

高中数学必修二第六章平面向量及其应用知识点归纳超级精简版单选题1、已知向量a ⃑,b ⃑⃑满足|a ⃑|=√3,|b ⃑⃑|=2,且a ⃑⊥(a ⃑−b ⃑⃑),则a ⃑与b ⃑⃑的夹角为( ) A .30°B .60°C .120°D .150° 答案:A分析:利用数量积的定义,即可求解.解:a ⃑⊥(a ⃑−b ⃑⃑),所以a ⃑⋅(a ⃑−b ⃑⃑)=0,即|a →|2−|a →||b →|cos <a →,b →>=0,解得cos <a →,b →>=√32,又因为向量夹角的范围为[0°,180°],则a ⃑与b ⃑⃑的夹角为30°,故选:A.2、“黄金三角形”是几何历史上的瑰宝,它有两种类型,其中一种是顶角为36°的等腰三角形,暂且称为“黄金三角形A ”.如图所示,已知五角星是由5个“黄金三角形A ”与1个正五边形组成,其中sin18°=√5−14,则阴影部分面积与五角形面积的比值为( ).A .√5−14B .√55C .√5+16D .3√520答案:B分析:在三角形ABC 中,由sin18°值,可得BCAC =√5−12,即BD AB=√5−12,设△ABC 的面积为x ,由此可知△BCD 和△CEF 的面积均为√5−12x ,△CDE 的面积为x ,由此即可求出结果.如图所示,依题意,在三角形ABC 中,sin18°=BC 2AC=√5−14,故BC AC=√5−12; 所以BDAB =√5−12, 设△ABC 的面积为x ,则△BCD 面积为√5−12x ,同理△CEF 的面积为√5−12x , △CDE 的面积为x ,则阴影部分面积与五角形面积的比值为2x+2⋅√5−12x 2⋅√5−12x+6x=√55. 故选:B .3、在△ABC 中,已知AB =6,AC =2,且满足DB ⃑⃑⃑⃑⃑⃑⃑=2AD ⃑⃑⃑⃑⃑⃑,AE ⃑⃑⃑⃑⃑⃑=EC ⃑⃑⃑⃑⃑⃑,若线段CD 和线段BE 的交点为P ,则AP⃑⃑⃑⃑⃑⃑⋅(CA ⃑⃑⃑⃑⃑⃑+CB ⃑⃑⃑⃑⃑⃑)=( ). A .3B .4C .5D .6 答案:B分析:待定系数法将AP ⃑⃑⃑⃑⃑⃑向量分解,由平面向量共线定理求出系数,然后代回原式计算 设AP⃑⃑⃑⃑⃑⃑=xAB ⃑⃑⃑⃑⃑⃑+yAC ⃑⃑⃑⃑⃑⃑, 由DB ⃑⃑⃑⃑⃑⃑⃑=2AD ⃑⃑⃑⃑⃑⃑知AB ⃑⃑⃑⃑⃑⃑=3AD ⃑⃑⃑⃑⃑⃑,∴AP ⃑⃑⃑⃑⃑⃑=3xAD ⃑⃑⃑⃑⃑⃑+yAC ⃑⃑⃑⃑⃑⃑,∵D ,P ,C 三点共线,∴3x +y =1①, 由AE⃑⃑⃑⃑⃑⃑=EC ⃑⃑⃑⃑⃑⃑知AC ⃑⃑⃑⃑⃑⃑=2AE ⃑⃑⃑⃑⃑⃑,∴AP ⃑⃑⃑⃑⃑⃑=xAB ⃑⃑⃑⃑⃑⃑+2yAE ⃑⃑⃑⃑⃑⃑,∵B ,P ,E 三点共线,∴x +2y =1②, 由①②得:x =15.y =25,∴AP ⃑⃑⃑⃑⃑⃑=15AB⃑⃑⃑⃑⃑⃑+25AC ⃑⃑⃑⃑⃑⃑, 而CA⃑⃑⃑⃑⃑⃑+CB ⃑⃑⃑⃑⃑⃑=−AC ⃑⃑⃑⃑⃑⃑+AB ⃑⃑⃑⃑⃑⃑−AC ⃑⃑⃑⃑⃑⃑=AB ⃑⃑⃑⃑⃑⃑−2AC ⃑⃑⃑⃑⃑⃑, ∴AP ⃑⃑⃑⃑⃑⃑⋅(CA ⃑⃑⃑⃑⃑⃑+CB ⃑⃑⃑⃑⃑⃑)=(15AB ⃑⃑⃑⃑⃑⃑+25AC ⃑⃑⃑⃑⃑⃑)(AB ⃑⃑⃑⃑⃑⃑−2AC ⃑⃑⃑⃑⃑⃑)=15(AB ⃑⃑⃑⃑⃑⃑2−4AC ⃑⃑⃑⃑⃑⃑2)=15×(62−4×22)=4 故选:B4、已知平面向量a ⃑=(1,2),b ⃑⃑=(-2,m ),且a ⃑∥b ⃑⃑,则2a ⃑+3b ⃑⃑=( ) A .(-4,-8)B .(-8,-16) C .(4,8)D .(8,16) 答案:A分析:根据向量平行的坐标表示求出m ,再根据向量线性运算得坐标表示即可求解. ∵a ⃑∥b ⃑⃑,∴1×m =2×(-2),∴m =-4,∴b ⃑⃑=(-2,-4), ∴2a ⃑+3b ⃑⃑=(2,4)+(-6,-12)=(-4,-8). 故选:A.5、已知向量a ⃑=(−1,m ),b ⃑⃑=(m +1,2),且a ⃑⊥b ⃑⃑,则m =( ) A .2B .−2C .1D .−1 答案:C分析:由向量垂直的坐标表示计算.由题意得a ⃑⋅b ⃑⃑=−m −1+2m =0,解得m =1 故选:C .6、在△ABC 中,cos C =23,AC =4,BC =3,则cos B =( )A .19B .13C .12D .23答案:A分析:根据已知条件结合余弦定理求得AB ,再根据cosB =AB 2+BC 2−AC 22AB⋅BC,即可求得答案.∵在△ABC 中,cosC =23,AC =4,BC =3根据余弦定理:AB 2=AC 2+BC 2−2AC ⋅BC ⋅cosCAB 2=42+32−2×4×3×23可得AB 2=9 ,即AB =3 由∵ cosB =AB 2+BC 2−AC 22AB⋅BC=9+9−162×3×3=19故cosB =19.故选:A.小提示:本题主要考查了余弦定理解三角形,考查了分析能力和计算能力,属于基础题. 7、在△ABC 中,角A,B,C 的对边分别是a,b,c ,若A =45°,B =60°,b =2√3,则c 等于( ) A .√6−√24B .√6+√24C .√6−√2D .√6+√2答案:D分析:先求出C ,再由正弦定理求解即可. 解:在△ABC 中,C =180°−45°−60°=75°. 由正弦定理可知csinC =bsinB ,所 以csin75°=2√3sin60°, 故c =2√3sin75°sin60°=4sin75°=4sin(30°+45°)=4×√6+√24=√6+√2.故选:D.8、已知向量|a ⃑|=2,|b ⃑⃑|=4,且a ⃑,b ⃑⃑不是方向相反的向量,则|a ⃑−b ⃑⃑|的取值范围是( ) A .(2,6)B .[2,6) C .(2,6]D .[2,6] 答案:B分析:直接由||a ⃑|−|b ⃑⃑||≤|a ⃑−b ⃑⃑|<|a ⃑|+|b⃑⃑|求解即可. 由已知必有||a ⃑|−|b ⃑⃑||≤|a ⃑−b ⃑⃑|<|a ⃑|+|b ⃑⃑|,则所求的取值范围是[2,6). 故选:B. 多选题9、如果平面向量a ⃗=(2,−4),b ⃑⃗=(−6,12),那么下列结论中正确的是( ) A .|b ⃑⃗|=3|a ⃗|B .a ⃗//b⃑⃗ C .a ⃗与b ⃑⃗的夹角为30°D .a ⃗在b ⃑⃗方向上的投影为2√5 答案:AB分析:根据向量坐标运算及向量共线的意义可得解.因为a ⃗=(2,−4),b ⃑⃗=(−6,12),所以b ⃑⃗=−3a ⃗. 在A 中,由b ⃑⃗=−3a ⃗,可得|b ⃑⃗|=3|a ⃗|,故A 正确; 在B 中,由b ⃑⃗=−3a ⃗,可得a ⃗//b⃑⃗,故B 正确; 在C 中,由b ⃑⃗=−3a ⃗,可得a ⃗与b⃑⃗的夹角为180°,故C 错误; 在D 中,a ⃗在b ⃑⃗方向上的投影为a ⃑⃗⋅b ⃑⃗|b ⃑⃗|=22=−2√5,故D 错误. 故选:AB .10、ΔABC 是边长为3的等边三角形,已知向量a ⃑、b ⃑⃑满足AB ⃑⃑⃑⃑⃑⃑=3a ⃑,AC ⃑⃑⃑⃑⃑⃑=3a ⃑+b ⃑⃑,则下列结论中正确的有( ) A .a ⃑为单位向量B .b ⃑⃑//BC ⃑⃑⃑⃑⃑⃑C .a ⃑⊥b ⃑⃑D .(6a ⃑+b ⃑⃑)⊥BC ⃑⃑⃑⃑⃑⃑ 答案:ABD解析:求出|a ⃑|可判断A 选项的正误;利用向量的减法法则求出b ⃑⃑,利用共线向量的基本定理可判断B 选项的正误;计算出a ⃑⋅b ⃑⃑,可判断C 选项的正误;计算出(6a ⃑+b⃑⃑)⋅BC ⃑⃑⃑⃑⃑⃑,可判断D 选项的正误.综合可得出结论. 对于A 选项,∵AB ⃑⃑⃑⃑⃑⃑=3a ⃑,∴a ⃑=13AB ⃑⃑⃑⃑⃑⃑,则|a ⃑|=13|AB⃑⃑⃑⃑⃑⃑|=1,A 选项正确; 对于B 选项,∵AC ⃑⃑⃑⃑⃑⃑=3a ⃑+b ⃑⃑=AB ⃑⃑⃑⃑⃑⃑+b ⃑⃑,∴b ⃑⃑=AC ⃑⃑⃑⃑⃑⃑−AB ⃑⃑⃑⃑⃑⃑=BC ⃑⃑⃑⃑⃑⃑,∴b ⃑⃑//BC ⃑⃑⃑⃑⃑⃑,B 选项正确; 对于C 选项,a ⃑⋅b ⃑⃑=13AB ⃑⃑⃑⃑⃑⃑⋅BC ⃑⃑⃑⃑⃑⃑=13×32×cos 2π3≠0,所以a ⃑与b ⃑⃑不垂直,C 选项错误; 对于D 选项,(6a ⃑+b ⃑⃑)⋅BC ⃑⃑⃑⃑⃑⃑=(AB ⃑⃑⃑⃑⃑⃑+AC ⃑⃑⃑⃑⃑⃑)⋅(AC ⃑⃑⃑⃑⃑⃑−AB ⃑⃑⃑⃑⃑⃑)=AC ⃑⃑⃑⃑⃑⃑2−AB ⃑⃑⃑⃑⃑⃑2=0,所以,(6a ⃑+b ⃑⃑)⊥BC ⃑⃑⃑⃑⃑⃑,D 选项正确. 故选:ABD.小提示:本题考查向量有关命题真假的判断,涉及单位向量、共线向量的概念的理解以及垂直向量的判断,考查推理能力,属于中等题.11、在△ABC 中,D ,E ,F 分别是边BC ,CA ,AB 的中点,点G 为△ABC 的重心,则下述结论中正确的是( ) A .AB ⃑⃑⃑⃑⃑⃑+BC ⃑⃑⃑⃑⃑⃑=CA ⃑⃑⃑⃑⃑⃑B .AG⃑⃑⃑⃑⃑⃑=12(AB ⃑⃑⃑⃑⃑⃑+AC ⃑⃑⃑⃑⃑⃑) C .AF ⃑⃑⃑⃑⃑⃑+BD ⃑⃑⃑⃑⃑⃑⃑+CE ⃑⃑⃑⃑⃑⃑=0⃑⃑D .GA ⃑⃑⃑⃑⃑⃑+GB ⃑⃑⃑⃑⃑⃑+GC ⃑⃑⃑⃑⃑⃑=0⃑⃑ 答案:CD分析:根据向量的加法运算、相反向量、中线的向量表示,重心的性质分别计算求解. 由D ,E ,F 分别是边BC ,CA ,AB 的中点,点G 为△ABC 的重心,因为AB⃑⃑⃑⃑⃑⃑+BC ⃑⃑⃑⃑⃑⃑=AC →≠CA ⃑⃑⃑⃑⃑⃑,故A 错误; 由12(AB⃑⃑⃑⃑⃑⃑+AC ⃑⃑⃑⃑⃑⃑)=AD →≠AG →, 故B 错误; 因为AF ⃑+BD ⃑+CE ⃑=12(AB →+BC →+CA →)=0⃑, 故C 正确;因为GA ⃑⃑⃑⃑⃑⃑+GB⃑⃑⃑⃑⃑⃑+GC ⃑⃑⃑⃑⃑⃑=−23[12(AB →+AC →)+12(BA →+BC →)+12(CA →+CB →)] =−13(AB →+BA →+BC →+CB →+AC →+CA →)=0→, 故D 正确. 故选:CD 填空题12、在△ABC 中, a =5,b =5√3,A =30°,则B =________. 答案:60°或120°分析:利用正弦定理求得sinB ,由此求得B . 由正弦定理得asinA=b sinB,即5sin30°=5√3sinB ⇒sinB =√32, 由于0°<B <180°,所以B =60°或B =120°. 所以答案是:60°或120°13、在△ABC 中,cos∠BAC =−13,AC =2,D 是边BC 上的点,且BD =2DC ,AD =DC ,则AB 等于 ___.答案:3分析:运用余弦定理,通过解方程组进行求解即可. 设DC =x,AB =y ,因为BD =2DC ,AD =DC ,所以BC =3x,AD =DC =x , 在△ADC 中,由余弦定理可知:cosC =AC 2+CD 2−AD 22AC⋅DC =4+x 2−x 24x=1x , 在△ABC 中,由余弦定理可知:cosC =AC 2+CB 2−AB 22AC⋅BC=4+9x 2−y 212x,于是有4+9x 2−y 212x=1x ⇒9x 2−y 2=8(1),在△ABC 中,由余弦定理可知:cosA =AB 2+CA 2−CB 22AB⋅AC=y 2+4−9x 24y=−13,⇒27x 2−3y 2−4y =12(2),把(1)代入(2)中得,y =3, 所以答案是:314、在△ABC 中,P 是BC 上一点,若BP ⃑⃑⃑⃑⃑⃑=2PC ⃑⃑⃑⃑⃑⃑,AP ⃑⃑⃑⃑⃑⃑=λAB ⃑⃑⃑⃑⃑⃑+μAC ⃑⃑⃑⃑⃑⃑,则2λ+μ=___________. 答案:43##113分析:根据给定条件,用向量AB ⃑⃑⃑⃑⃑⃑,AC ⃑⃑⃑⃑⃑⃑表示向量AP ⃑⃑⃑⃑⃑⃑,再利用平面向量基本定理求解作答. 在△ABC 中,BP ⃑⃑⃑⃑⃑⃑=2PC ⃑⃑⃑⃑⃑⃑,则AP ⃑⃑⃑⃑⃑⃑=AB ⃑⃑⃑⃑⃑⃑+BP ⃑⃑⃑⃑⃑⃑=AB⃑⃑⃑⃑⃑⃑+23BC ⃑⃑⃑⃑⃑⃑=AB ⃑⃑⃑⃑⃑⃑+23(AC ⃑⃑⃑⃑⃑⃑−AB ⃑⃑⃑⃑⃑⃑) =13AB ⃑⃑⃑⃑⃑⃑+23AC ⃑⃑⃑⃑⃑⃑, 又AP ⃑⃑⃑⃑⃑⃑=λAB ⃑⃑⃑⃑⃑⃑+μAC ⃑⃑⃑⃑⃑⃑,且AB ⃑⃑⃑⃑⃑⃑,AC ⃑⃑⃑⃑⃑⃑不共线,则λ=13,μ=23,所以2λ+μ=43. 所以答案是:43解答题15、已知函数f (x )=4cosxsin (x −π3)+√3. (Ⅰ)求函数f (x )在区间[π4,π2]上的值域.(Ⅱ)在△ABC 中,角A ,B ,C ,所对的边分别是a ,b ,c ,若角C 为锐角,f (C )=√3,且c =2,求△ABC 面积的最大值.答案:(Ⅰ)[1,2];(Ⅱ)√3分析:(Ⅰ)利用差角的正弦公式、辅助角公式化简函数,结合正弦函数的性质,可得函数f(x)在区间[π4,π2]上的值域;(Ⅱ)先求出C ,再利用余弦定理,结合基本不等式,即可求得△ABC 面积的最大值. 解:(Ⅰ)f(x)=4cosxsin(x −π3)+√3=4cosx (sinxcos π3−cosxsin π3)+√3=4cosx (12sinx −√32cosx)+√3=2sinxcosx −2√3cos 2x +√3=sin2x −√3cos2x =2sin(2x −π3),由π4⩽x⩽π2,有π6⩽2x−π3⩽2π3,所以12≤sin(2x−π3)≤1∴函数f(x)的值域为[1,2].(Ⅱ)由f(C)=√3,有sin(2C−π3)=√32,∵C为锐角,∴2C−π3=π3,∴C=π3.∵c=2,∴由余弦定理得:a2+b2−ab=4,∵a2+b2⩾2ab,∴4=a2+b2−ab⩾ab.∴S△ABC=12absinC=√34ab⩽√3,∴当a=b,即△ABC为正三角形时,△ABC的面积有最大值√3.。
人教版高中数学必修第二册6.2.1-6.2.2 向量的减法运算 向量的加法运算 同步精练(含解析)
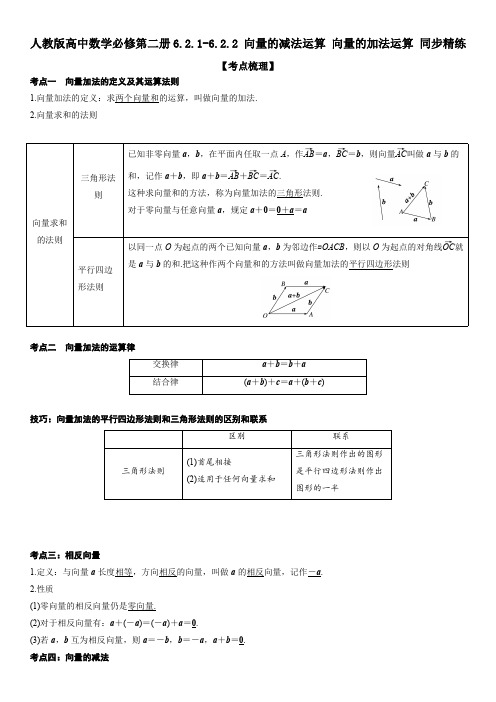
人教版高中数学必修第二册6.2.1-6.2.2向量的减法运算向量的加法运算同步精练【考点梳理】考点一向量加法的定义及其运算法则1.向量加法的定义:求两个向量和的运算,叫做向量的加法.2.向量求和的法则考点二向量加法的运算律交换律a +b =b +a 结合律(a +b )+c =a +(b +c )技巧:向量加法的平行四边形法则和三角形法则的区别和联系区别联系三角形法则(1)首尾相接(2)适用于任何向量求和三角形法则作出的图形是平行四边形法则作出图形的一半考点三:相反向量1.定义:与向量a 长度相等,方向相反的向量,叫做a 的相反向量,记作-a .2.性质(1)零向量的相反向量仍是零向量.(2)对于相反向量有:a +(-a )=(-a )+a =0.(3)若a ,b 互为相反向量,则a =-b ,b =-a ,a +b =0.考点四:向量的减法向量求和的法则三角形法则已知非零向量a ,b ,在平面内任取一点A ,作AB →=a ,BC →=b ,则向量AC →叫做a 与b 的和,记作a +b ,即a +b =AB →+BC →=AC →.这种求向量和的方法,称为向量加法的三角形法则.对于零向量与任意向量a ,规定a +0=0+a =a平行四边形法则以同一点O 为起点的两个已知向量a ,b 为邻边作▱OACB ,则以O 为起点的对角线OC →就是a 与b 的和.把这种作两个向量和的方法叫做向量加法的平行四边形法则1.定义:向量a加上b的相反向量,叫做a与b的差,即a-b=a+(-b),因此减去一个向量,相当于加上这个向量的相反向量,求两个向量差的运算,叫做向量的减法.2.几何意义:在平面内任取一点O,作OA→=a,OB→=b,则向量a-b=BA→,如图所示.3.文字叙述:如果把两个向量的起点放在一起,那么这两个向量的差是以减向量的终点为起点,被减向量的终点为终点的向量.【题型归纳】题型一:向量加法法则1.(2021·全国·高一课时练习)如图,已知向量a,b,c不共线,作向量a+b+c.2.(2021·全国·高一课时练习)如图,已知向量a,b不共线,求作向量a b .3.(2021·全国·高一课时练习)如图,O 为正六边形ABCDEF 的中心,作出下列向量:(1)OA OC +;(2)BC FE +(3)OA FE +.题型二:向量加法的运算律4.(2021·陕西·宝鸡市陈仓区教育体育局教学研究室高一期中)向量AB CB BD BE DC ++++化简后等于()A .A EB .ACC .ADD .AB5.(2021·全国·高一课时练习)如图,四边形ABCD 是梯形,AD ∥BC ,对角线AC 与BD 相交于点O ,则OA BC AB DO +++等于()A .CDB .DC C .DAD .DO6.(2021·广东·茂名市华英学校高一阶段练习)向量()()AB PB BO BM OP ++++化简后等于()A .BCB .ABC .ACD .AM题型三:向量加法法则的几何应用7.(2021·全国·高一课时练习)如图,D ,E ,F 分别为ABC 的边AB ,BC ,CA 的中点,则()A .0AD BE CF ++=B .0++=BD CF DFC .0++=AD CE CF D .0++=BD BE FC 8.(2021·全国·高一课时练习)如图,在正六边形ABCDEF 中,BA CD FB ++等于()A .0B .BEC .AD D .CF9.(2021·江西省修水县英才高级中学高一阶段练习)如图,在平行四边形ABCD 中,E 是CD 的中点,设AB a =,AD b =,则向量BE =().A .12a b-B .12a b-+C .12a b-D .12a b-+题型四:相反向量10.(2021·辽宁·建平县实验中学高一期末)如图,在四边形ABCD 中,AC 与BD 交于点O ,若AD BC =,则下面互为相反向量的是()A .AC 与CBB .OB 与ODuuu rC .AB 与DCD .AO 与OC11.(2021·山西临汾·高一阶段练习)在任意四边形ABCD 中,E ,F 分别为AD ,BC 的中点,设,AB a CD b ==,下列式子正确的是()A .2a b EF+=B .2a b EF-=C .a b EF+=D .a b EF-=12.(2021·全国·高一单元测试)若b 是a 的负向量,则下列说法中错误的是()A .a 与b 的长度必相等B .//a bC .a 与b 一定不相等D .a 是b 的负向量题型五:向量减法法则13.(2021·全国·高一课时练习)如图,已知向量a ,b ,c ,求作向量a b c --.14.(2021·全国·高一课时练习)如图,点O 是ABCD 的两条对角线的交点,AB a =,DA b =,OC c =,求证:b c a OA +-=.15.(2021·全国·高一课时练习)如图,已知OA a =,OB b =,OC c =,OD d =,OF f =,试用a ,b ,c ,d ,f r表示以下向量:(1)AC ;(2)AD ;(3)AD AB -;(4)AB CF +;(5)BF BD -.题型六:向量减法的运算律16.(2021·全国·高一课时练习)下列运算正确的个数是()①()326a a -⋅=-;②()()223a b b a a +--=;③()()220a b b a +-+=.A .0B .1C .2D .317.(2021·北京市第一六六中学高一期中)在ABC 中,13BD BC =,若AB a =,AC b =,则AD =()A .1233a b-B .1233a b+C .2133a b+D .2133a b-18.(2021·浙江·金乡卫城中学高一阶段练习)在平行四边形ABCD 中,设M 为线段BC 的中点,N 为线段AB 上靠近A 的三等分点,AB a =,AD b =,则向量NM =()A .1132a b+B .2132a b+C .1132a b-D .2132a b-题型七:向量减法法则的几何应用19.(2021·全国·高一课时练习)已知非零向量a 与b 方向相反,则下列等式中成立的是()A .a b a b -=-B .a b a b +=-C .a b a b+=-D .a b a b+=+20.(2021·全国·高一单元测试)已知正方形ABCD 的边长为1,AB a =,BC b =,AC c =,则||a b c +-等于()A .0B .1C .2D .221.(2021·全国·高一课时练习)如图,向量AB a →=,AC b →=,CD c →=,则向量BD →可以表示为()A .a b c --B .b a c +-C .a b c-+D .b a c-+【双基达标】一:单选题22.(2021·全国·高一课时练习)化简下列各式:①AB BC CA ++;②()AB MB BO OM +++uu u r uuu r uu u r uuu r;③OA OC BO CO +++;④AB CA BD DC +++.其中结果为0的个数是()A .1B .2C .3D .423.(2021·全国·高一课时练习)已知a 、b 是不平行的向量,若2AB a b =+,4BC a b =--,53CD a b =--,则下列关系中正确的是()A .AD CB =B .AD BC =C .2AD BC=D .2AD BC=-24.(2021·全国·高一课时练习)若非零向量a 和b 互为相反向量,则下列说法中错误的是().A .//a br r B .a b≠C .a b≠r r D .b a=-25.(2021·全国·高一课时练习)已知点O 是ABCD 的两条对角线的交点,则下面结论中正确的是().A .AB CB AC +=B .AB AD AC+=C .AD CD BD+≠D .0AO CO OB OD +++≠26.(2021·全国·高一课时练习)下列四式不能化简为PQ 的是()A .()AB PA BQ ++B .()()AB PC BA QC ++-C .QC CQ QP +-D .PA AB BQ+-27.(2021·全国·高一课时练习)已知六边形ABCDEF 是一个正六边形,O 是它的中心,其中,,OA a OB b OC c ===,则EF =()A .a b +B .b a -C .-c bD .b c-r r28.(2021·全国·高一课前预习)下列等式中,正确的个数为()①0a a -=-;②()a a --=;③()0a a +-=;④0a a +=;⑤()a b a b -=+-;⑥()0a a --=.A .3B .4C .5D .629.(2021·重庆实验外国语学校高一阶段练习)如右图,D ,E ,P 分别是ABC 的边AB ,BC ,CA 的中点,则()A .0AD BE CF ++=B .0BD CF DF -+=uu u r uu u r uuu r rC .0AD CE CF +-=uuu r uur uu u r r D .0BD BE FC --=30.(2021·山东济南·高一期末)在ABC 中,若点D 满足3BC DC =,则()A .1233AD AB AC =+B .2133AD AB AC =-C .1344AD AB AC =+D .3144AD AB AC =-31.(2021·山东滨州·高一期末)在ABC 中,2BD DC =,AE ED =,则BE =()A .1536AC AB-+B .1536AC AB-C .1136AC AB-+D .1136AC AB-【高分突破】一:单选题32.(2021·全国·高一课时练习)设()()a AB CD BC DA =+++,b 是任一非零向量,则在下列结论中:①//a b r r;②a b a +=;③a b b +=;④a b a b +<+;⑤a b a b +=+.正确结论的序号是()A .①⑤B .②④⑤C .③⑤D .①③⑤33.(2021·山东枣庄·高一期中)已知点G 是三角形ABC 所在平面内一点,满足0GA GB GC ++=,则G 点是三角形ABC 的()A .垂心B .内心C .外心D .重心34.(2021·全国·高一课时练习)下列命题中正确的是()A .如果非零向量a 与b 的方向相同或相反,那么a b +的方向必与a ,b 之一的方向相同B .在ABC 中,必有0AB BC CA ++=C .若0AB BC CA ++=,则A ,B ,C 为一个三角形的三个顶点D .若a ,b 均为非零向量,则||a b +与||||a b +一定相等35.(2021·福建·莆田第二十五中学高一期中)如图,已知OA a =,OB b =,OC c =,2AB BC =,则下列等式中成立的是()A .2c a b =-B .2=-c b aC .3122c b a =-D .3122c a b =-36.(2021·安徽·六安市裕安区新安中学高一期中)在平行四边形ABCD 中,14AE AC =,设AB a =,BC b =,则向量DE =uuu r ()A .1344a b-B .3144a b-C .2133a b-D .1233a b-37.(2021·湖南·高一阶段练习)在ABC 中,点E ,F 在边AB 上,且E ,F 为AB 边上的三等分点(其中E 为靠近点A 的三等分点),且CE mCB nCA =+,则()A .23m =,13n =-B .13m =,23n =C .23m =,13n =D .13m =,23n =-38.(2021·全国·高一课时练习)(多选)下列结论中错误的是()A .两个向量的和仍是一个向量B .向量a 与b 的和是以a 的始点为始点,以b 的终点为终点的向量C .0a a+=D .向量a 与b 都是单位向量,则||2a b +=r r 39.(2021·广东·江门市新会第二中学高一阶段练习)下列各式结果为零向量的有()A .AB CA BC→→→++B .AB AC BD CD+++C .OA OD AD-+D .NQ QP MN MP++-40.(2021·广东·南方科技大学附属中学高一期中)已知点D ,E ,F 分别是ABC 的边,,AB BC AC 的中点,则下列等式中正确的是()A .FD DA FA +=B .0FD DE EF ++=C .DE DA EC+=D .DA DE FD+=41.(2021·江苏·南京二十七中高一期中)已知OD OE OM +=,则下列结论正确的是()A .OD EO OM +=B .OM DO OE +=C .OM OE OD-=D .DO EO MO+=42.(2021·广东·洛城中学高一阶段练习)化简以下各式,结果为0的有()A .AB BC CA ++B .AB AC BD CD -+-C .OA OD AD-+D .NQ QP MN MP++-43.(2021·福建·永安市第三中学高中校高一阶段练习)下列命题中,正确的命题为()A .对于向量,a b ,若||||a b =,则a b =或=-a bB .若e 为单位向量,且a //e ,则||a a e =±C .若a 与b 共线,b 与c 共线,则a 与c 共线D .四边形ABCD 中,AB CD AD CB+=+uu u r uu u r uuu r uu r 二:填空题44.(2021·全国·高一课时练习)已知平面内三个不同的点A 、B 、C ,则“A 、B 、C 是一个三角形的三个顶点”是“0AB BC AC ++=”的___________条件.(填“充分不必要”、“必要不充分”或“充要”)45.(2021·全国·高一课时练习)已知下列各式:①AB BC CA ++;②()AB MB BO OM +++;③OA OC BO CO +++;④AB CA BD DC +++.其中结果为0的是____.(填序号)46.(2021·全国·高一课时练习)在ABC 中,D 是BC 的中点.若AB c =,AC b =,BD a =,d AD =,则下列结论中成立的是________.(填序号)①d a b -=;(2)d a b -=-;③d a c -=;④d a c -=-.47.(2021·全国·高一课时练习)如图,在正六边形ABCDEF 中,与OA OC CD -+相等的向量有__.①CF ;②AD ;③BE ;④DE FE CD -+;⑤CE BC +;⑥CA CD -;⑦AB AE +.三:解答题48.(2021·全国·高一课时练习)化简.(1)AB CD BC DA +++.(2)()()AB MB BO BC OM ++++.49.(2021·上海·高一课时练习)向量,,,,a b c d e r r r u r r 如图所示,据图解答下列问题:(1)用,,a d e 表示DB ;(2)用,b c 表示DB ;(3)用,,a b e 表示EC ;(4)用,d c 表示EC .50.(2021·全国·高一课时练习)化简:(1)AB BC CA ++;(2) ()AB MB BO OM +++;(3)OA OC BO CO +++;(4)AB AC BD CD -+-;(5)OA OD AD -+;(6)AB AD DC --;(7)NQ QP MN MP ++-.51.(2021·全国·高一课时练习)如图,四边形OADB 是以向量OA a =,OB b =为边的平行四边形,又13BM BC =,13CN CD =,试用a 、b 表示OM 、ON 、MN .【答案详解】【详解】由向量加法的三角形法则,a +b +c 如图,2.作图见解析,BA a b=-【分析】利用向量的加法法则求解.【详解】如图,在平面内任取一点O ,作OA a =,OB b =.因为OB BA OA +=,即b BA a +=,所以BA a b =-.3.(1)答案见解析(2)答案见解析(3)答案见解析【分析】利用向量加法的三角形法则或平行四边形法则进行求解﹒(1)因为四边形OABC 是以OA ,OC 为邻边的平行四边形,OB 为其对角线,所以OA OC OB +=uu r uuu r uu u r .(2)因为BC 与FE 方向相同且长度相等,所以BC 与FE 是相同的向量,从而BC FE +与BC 方向相同,长度为BC 长度的2倍,因此,BC FE +可用AD 表示,即BC FE AD +=.(3)因为OA 与FE 是一对相反向量,所以0OA FE +=.4.A【分析】根据向量的线性运算求解即可.【详解】由AB CB BD BE DC AC CB BE AE →→++++=++=,故选:A5.B【分析】利用向量加法的三角形法则以及向量加法的交换律即可求解.【详解】OA BC AB DO DO OA AB BC DC =++++=++.故选:B6.D【分析】根据向量的加法运算即可得到结果.【详解】()()()()AB PB BO BM OP AB BM PB BO OP AM++++=++++=故选:D7.A【分析】根据平面向量的线性运算法则计算可得;【详解】解:D Q ,E ,F 分别是ABC 的边AB ,BC ,CA 的中点,∴12AD AB =,12BE BC =,12CF CA =,则1111()02222AD BE CF CA AB CA CA AB CA ++=++=++=,故A 正确;()1111122222BD CF DF BA CA BA CA BA BC BC ++=++=++=,故B 错误;()1111122222AD CE CF AB CB CA CA AB CB CB ++=++=++=,故C 错误;()1111122222BD BE FC BA BC AC BA AC BC BC ++=++=++=,故D 错误;故选:A .8.A【分析】根据相等向量和向量加法运算直接计算即可.【详解】CD AF =,∴0BA CD FB BA AF FB ++==++.故选:A.9.B【分析】根据平行四边形的性质,利用向量加法的几何意义有BE BC CE =+,即可得到BE 与a 、b 的线性关系.【详解】由题设,AB DC a ==,则12EC a =,又AD BC b ==uuu r uu u r r ,∴12BE BC CE b a =+=-.故选:B10.B【分析】首先根据题意得到四边形ABCD 是平行四边形,从而得到OB 与OD uuu r 为相反向量.【详解】因为AD BC =,所以四边形ABCD 是平行四边形,所以AC ,BD 互相平分,所以OB OD =-,即OB 与OD uuu r 为相反向量.故选:B11.B【分析】根据题意,由向量的加法可得:EF EA AB BF =++和 EF ED DC CF =++,两个式子相加,化简即可得到答案.【详解】在任意四边形ABCD 中,E ,F 分别为AD ,BC 的中点,设,AB a CD b ==,则EF EA AB BF =++,同时有 EF ED DC CF =++,则有2 EF EA ED AB DC BF CF =+++++,因为E 、F 分别为AD,BC 的中点,则0, 0EA ED BF CF +=+=则有2a b EF -=.故选:B.12.C【分析】根据向量的定义判断.【详解】b 是a 的负向量,即b a =-,因此它们的长度相等,方向相反,即共线(平行),a 也是b 的负向量,但a 与b 一般不相等(只有它们为零向量时相等).错误的C .故选:C .13.见解析【分析】利用向量减法的三角形法则即可求解.【详解】由向量减法的三角形法则,令,a OA b OB →→→==,则a b OA OB BA →→→→→-=-=,令c BC →→=,所以a b c BA BC CA →→→--=-=.如下图中CA →即为a b c --.14.证明见解析【分析】利用向量的加法法则和向量相等求解.【详解】证明:因为四边形ABCD 是平行四边形,所以DA CB =.因为b c DA OC OC CB OB +=+=+=,OA a OA AB OB +=+=,所以b c OA a +=+,即b c a OA +-=.15.(1)c a→→-(2)d a→→-(3)d b→→-(4)b a f c→→→→-+-(5)f d→→-【分析】由向量减法法则依次计算即可得出各小问的结果.(1)AC OC OA c a →→→→=-=-.(2)AD OD OA d a →→→→=-=-.(3)AD AB BD OD OB d b →→→→→-==-=-.(4)AB CF OB OA OF OC b a f c →→→→→→→→+=-+-=-+-.(5)BF BD DF OF OD f d →→→→→-==-=-.16.C【分析】利用平面向量的加法,减法,数乘运算及其运算律判断.【详解】①()326a a -⋅=-,由数乘运算知正确;②()()223a b b a a +--=,由向量的运算律知正确;③()()220a b b a +-+=,向量的加法,减法和数乘运算结果是向量,故错误.故选:C17.C【分析】根据平面向量的线性运算法则,用AB ,AC ,表示出AD 即可.【详解】()112121333333AD AB BD AB BC AB AC AB AB AC a b =+=+=+-=+=+.故选:C18.B【分析】根据题意作出图形,将AM 用a 、b 的表达式加以表示,再利用平面向量的减法法则可得出结果.【详解】解:由题意作出图形:在平行四边形ABCD 中,M 为BC 的中点,则12AM AB BM a b =+=+又N 为线段AB 上靠近A 的三等分点,则1133AN AB a ==11212332NM AM AN a b a a b ∴=-=+-=+故选:B19.C【分析】根据方向相反的两个向量的和或差的运算逐一判断.【详解】A.a b -可能等于零,大于零,小于零,0a b a b -=+>,A 不成立B.a b a b +=-r r r r ,a b a b -=+,B 不成立C.a b a b -=+,C 成立D.a b a b a b +=-≠+,D 不成立.故选:C.20.A【分析】根据向量的线性运算即可求出.【详解】因为AB a =,BC b =,AC c =,所以0a b c AB BC AC AC AC +-=+-=-=.故选:A .21.D【分析】根据平面向量的加减法法则结合图形即可得到答案.【详解】如图,BD BC CD AC AB CD b a c →→→→→→→→→=+=-+=-+.故选:D.22.B【分析】根据向量的加减运算法则计算,逐一判断①②③④的正确性,即可得正确答案.【详解】对于①:0AB BC CA AC CA ++=+=,对于②:()AB MB BO OM AB BO OM MB AM MB AB +++=+++=+=uu u r uuu r uu u r uuu r uu u r uu u r uuu r uuu r uuu r uuu r uu u r,对于③:()()0OA OC BO CO BO OA CO OC BA BA +++=+++=+=,对于④:()()0AB CA BD DC AB BD DC CA AD DA +++=+++=+=,所以结果为0的个数是2,故选:B23.C【分析】结合向量的加法法则运算即可.【详解】AD =AB +BC +CD =8a -2b -=()24a b --=2BC .故选:C24.C【分析】根据相反向量的定义逐项判断即可.【详解】解:由平行向量的定义可知A 项正确;因为a 和b 的方向相反,所以a b ≠,故B 项正确;由相反向量的定义可知a b =-,故选D 项正确;由相反向量的定义知||||a b =,故C 项错误;故选:C .25.B【分析】根据平面向量线性运算法则计算可得;【详解】对于A :AB CB AB DA DB +=+=,故A 错误;对于B :AB AD AC +=,故B 正确;对于C :A B AD CD D B A D +=+=,故C 错误;对于D :0AO CO OB OD +++=,故D 错误;故选:B26.D【分析】由向量加减法法则计算各选项,即可得结论.【详解】A 项中,()()AB PA BQ AB BQ AP AQ AP PQ ++=+-=-=;B 项中,()()()()AB PC BA QC AB AB PC CQ PQ ++-=-++=;C 项中,QC CQ QP QP PQ +-=-=;D 项中,PA AB BQ PB BQ PQ +-=-≠.故选:D.27.D【分析】由图形可得EF CB OB OC ==-,从而可得正确的选项.【详解】EF CB OB OC b c -=-==,故选:D.28.C【分析】利用向量加减法的运算性质,转化各项表达式即可知正误.【详解】由向量加减法的运算性质知:①0a a -=-;②()a a --=;③()0a a +-=;④0a a +=;⑤()a b a b -=+-,正确;⑥()2a a a a a --=+=,错误.故选:C29.A【分析】根据向量加法和减法的运算法则结合图像逐一运算即可得出答案.【详解】解:0AD BE CF DB BE ED DE ED ++=++=+=,故A 正确;BD CF DF BD FC DF BC -+=++=,故B 错误;AD CE CF AD FE AD DB AB +-=+=+=,故C 错误;2BD BE FC ED FC ED DE ED --=-=-=,故D 错误.故选:A.30.A【分析】利用向量加减法公式,化简已知条件,即可判断结果.【详解】由条件可知()3AC AB AC AD -=-,得1233AD AB AC =+.故选:A31.B【分析】利用向量加法和减法计算即可求解.【详解】()1122BE AE AB AD AB AC CD AB =-=-=+-()11112323AC CB AB AC AB AC AB ⎛⎫⎡⎤=+-=+-- ⎪⎢⎥⎝⎭⎣⎦1211523336AC AB AB AC AB ⎛⎫=+-=- ⎪⎝⎭,故选:B.32.D【分析】根据向量线性运算可确定a 为零向量,由此可判断得到结果.【详解】()()()()0a AB CD BC DA AB BC CD DA AC CA =+++=+++=+=,又b 是任一非零向量,//a b ∴,a b b +=,a b a b +=+,∴①③⑤正确.故选:D.33.D【分析】由题易得GA GB CG +=,以GA 、GB 为邻边作平行四边形GADB ,连接GD ,交AB 于点O ,进而可得CG GD =,进而可得13GO CO =,所以CG 所在的直线CO 是AB 边上的中线,同理可证AG 所在的直线是BC 边上的中线,BG 所在的直线是AC 边上的中线,最后得出答案即可.【详解】因为0GA GB GC ++=,所以GA GB GC CG +=-=,以GA 、GB 为邻边作平行四边形GADB ,连接GD ,交AB 于点O ,如图所示:则CG GD =,所以13GO CO =,点O 是AB 边的中点,所以CG 所在的直线CO 是AB 边上的中线,同理可证AG 所在的直线是BC 边上的中线,BG 所在的直线是AC 边上的中线,所以G 点是三角形ABC 的重心.故选:D .34.B【分析】根据向量的线性运算法则,逐一分析各个选项,即可得答案.【详解】对于A :当a 与b 为相反向量时,0a b +=,方向任意,故A 错误;对于B :在ABC 中,0AB BC CA ++=,故B 正确;对于C :当A 、B 、C 三点共线时,满足0AB BC CA ++=,但不能构成三角形,故C 错误;对于D :若a ,b 均为非零向量,则a b a b +≤+,当且仅当a 与b 同向时等号成立,故D 错误.故选:B35.C【分析】结合图形,利用向量加,减法,计算向量.【详解】2AB BC =,()2OB OA OC OB ∴-=-,得3122OC OB OA =-,即3122c b a =-r r r .故选:C36.A【分析】利用向量的加、减法法则计算即可.【详解】解:()()1111344444DE AE AD AC BC AB BC BC a b b a b =-=-=+-=+-=-.故选:A.37.B【分析】利用向量的加法、减法线性运算即可求解.【详解】()22123333CE CB BE CB BA CB CA CB CB CA ==+=++-=+,所以13m =,23n =.故选:B38.BD【分析】根据向量的相关概念,对选项逐一判断即可.【详解】两个向量的和差运算结果都是是一个向量,所以A 正确;两个向量的加法遵循三角形法则,只有当,a b 首尾相连时才成立,故B 错误;任何向量与0相加都得其本身,故C 正确;两个单位向量的方向没有确定,当它们方向相同时才成立,故D 错误;故选:BD39.ACD【分析】根据平面向量的线性运算逐个求解即可【详解】对A ,0AB CA BC CA AB BC CB BC ++=++=+=,故A 正确;对B ,()()2AB AC BD CD AB BD AC CD AD AD AD +++=+++=+=,故B 错误;对C ,0OA OD AD DA AD -+=+=,故C 正确;对D ,0NQ QP MN MP NP PN ++-=+=,故D 正确;故选:ACD【点睛】本题主要考查了平面向量的线性运算,属于基础题40.ABC【分析】根据向量线性运算确定正确选项.【详解】对于A 选项,FD DA FA +=,正确;对于B 选项,0FD DE EF FE EF ++=+=,正确;对于C 选项,根据向量加法的平行四边形法则可知DE DA DF EC =+=,正确;对于D 选项,DA DE DF FD +=≠,所以D 错误.故选:ABC41.BCD【分析】根据向量的线性运算,逐项变形移项即可得解.【详解】根据复数的线性运算,对A ,化简为OD EO ED +=,错误;对B ,即OM OD OE -=,即OD OE OM +=,正确;对C ,对OM OE OD -=移项可得OD OE OM +=,正确;对D ,由OD OE OM --=-,移项即OD OE OM +=,正确;故选:BCD42.ABCD【分析】根据向量的加减运算法则分别判断.【详解】0AB BC CA ++=,0AB AC BD CD AB BD AC CD AD AD -+-=+--=-=,0OA OD AD OA AD OD -+=+-=,0NQ QP MN MP NP PN ++-=+=.所以选项全正确.故选:ABCD43.BD【分析】直接利用向量的线性运算,向量的共线,单位向量的应用判断A 、B 、C 、D 的结论.【详解】对于A :对于向量,a b ,若||||a b =,则a 与b 不存在关系,故A 错误;对于B :若e 为单位向量,且//a e ,则||a a e =±,故B 正确;对于C :若a 与b 共线,b 与c 共线,且0b ≠,则a 与c 共线,当=0b ,则a 与c 不一定共线,故C 错误;对于D :四边形ABCD 中,AB CD AD CB +=+uu u r uu u r uuu r uu r ,整理得AB AD CB CD DB -=-=,故D 正确;故选:BD .44.充分不必要【分析】利用向量加法的三角形法则结合充分条件、必要条件的定义判断可得出结论.【详解】充分性:若A 、B 、C 是一个三角形的三个顶点,由平面向量加法的三角形法则可得出0AB BC AC ++=,充分性成立;必要性:若A 、B 、C 三点共线,则0AB BC AC ++=成立,此时A 、B 、C 不能构成三角形,必要性不成立.因此,“A 、B 、C 是一个三角形的三个顶点”是“0AB BC AC ++=”的充分不必要条件.故答案为:充分不必要.45.①④【分析】利用向量加法的运算法则化简各项向量的线性表达式,即可确定结果是否为0.【详解】①0AB BC CA AC CA ++=+=uu u r uu u r uu r uuu r uu r r ;②()()()0AB MB BO OM AB BO OM MB AO OB AB +++=+++=+=≠;③0OA OC BO CO OA BO BA +++=+=≠;④()()0AB CA BD DC CA AB BD DC CB BC +++=+++=+=.故答案为:①④.46.③【分析】根据平面向量的加减法判断即可.【详解】d a AD BD AB c -=-==,故③成立;故答案为:③47.①④【分析】根据向量加减法运算可化简OA OC CD -+为CF ,根据相等向量的定义依次判断各个选项即可得到结果.【详解】四边形ACDF 是平行四边形,OA OC CD CA CD CF ∴-+=+=,①正确;AD 与CF 方向不同,②错误;BE 与CF 方向不同,③错误;DE FE CD CE FE CE EF CF -+=-=+=,④正确;CE BC CE CB BE +=-=,⑤错误;CA CD DA -=与CF 方向不同,⑥错误;四边形ABDE 为平行四边形,AB AE AD ∴+=,⑦错误.故答案为:①④.48.(1)0;(2)AC .【分析】(1)利用平面向量加法的三角形法则化简可得所求代数式的结果;(2)利用平面向量加法的三角形法则化简可得所求代数式的结果.【详解】(1)0AB CD BC DA AB BC CD DA +++=+++=;(2)()()AB MB BO BC OM AB BO OM MB BC AC ++++=++++=.49.(1)DB d e a =++uu u r u r r r ;(2)DB b c =--uu u r r r ;(3)EC e a b =++uu u r r r r ;(4)EC c d =--uu u r r u r .【分析】利用向量的加法法则、减法法则运算即可【详解】由图知,,,,AB a BC b CD c DE d EA e =====,(1)DB DE EA AB d e a =++=++;(2)DB CB CD BC CD b c =-=--=--;(3)EC EA AB BC e a b =++=++;(4)()EC CE CD DE c d=-=-+=--50.(1)0.(2)AB (3)BA .(4)0(5)0(6)CB .(7)0解:(1)原式0AC AC =-=.(2)原式AB BO OM MB AB=+++=(3)原式OA OC OB OC BA =+--=.(4)原式0AB BD DC CA =+++=(5)原式0OA AD DO =++=(6)原式()AB AD DC AB AC CB =-+=-=.(7)原式0MN NQ QP PM =+++=【点睛】本题考查了平面向量的加法与减法的运算问题,属于基础题.51.解:13BM BC =,BC CA =,16BM BA ∴=,∴111()()666BM BA OA OB a b ==-=-.∴()115666OM OB BM b a b a b =+=+-=+.13CN CD =,CD OC =,∴2222()3333ON OC CN OD OA OB a b =+==+=+.∴221511336626MN ON OM a b a b a b =-=+--=-.。
高中数学向量的运算技巧及应用举例

高中数学向量的运算技巧及应用举例向量是高中数学中的重要概念,它不仅在几何中有广泛的应用,还在物理学、工程学等领域中发挥着重要作用。
掌握向量的运算技巧和应用,对于高中学生来说至关重要。
本文将以具体的题目为例,详细介绍向量的运算技巧及其应用。
一、向量的加法和减法向量的加法和减法是向量运算中最基础的部分。
在进行向量的加减运算时,需要注意向量的方向和大小。
例题1:已知向量a = (2, 3)和向量b = (-1, 4),求向量c = a + b。
解析:根据向量的加法定义,向量c的横坐标等于向量a和向量b的横坐标之和,纵坐标等于向量a和向量b的纵坐标之和。
因此,向量c = (2 + (-1), 3 + 4) = (1, 7)。
例题2:已知向量a = (3, 5)和向量b = (2, -4),求向量c = a - b。
解析:根据向量的减法定义,向量c的横坐标等于向量a和向量b的横坐标之差,纵坐标等于向量a和向量b的纵坐标之差。
因此,向量c = (3 - 2, 5 - (-4)) = (1, 9)。
通过以上两个例题,我们可以看出向量的加法和减法运算实际上就是对应坐标的加减运算。
掌握了这一点,我们就能够轻松地进行向量的加减运算。
二、向量的数量积和向量积向量的数量积和向量积是向量运算中的两个重要概念。
数量积表示两个向量的乘积,向量积表示两个向量的叉乘。
例题3:已知向量a = (3, 4)和向量b = (2, -1),求向量a和向量b的数量积。
解析:向量a和向量b的数量积等于向量a的横坐标乘以向量b的横坐标之和,再加上向量a的纵坐标乘以向量b的纵坐标之和。
因此,向量a和向量b的数量积为3 * 2 + 4 * (-1) = 6 - 4 = 2。
例题4:已知向量a = (3, 4)和向量b = (2, -1),求向量a和向量b的向量积。
解析:向量a和向量b的向量积等于向量a的横坐标乘以向量b的纵坐标减去向量a的纵坐标乘以向量b的横坐标。
高一7-1向量概念、加减运算知识梳理、经典例题、课后练习带答案

环 球 雅 思 教 育 学 科 教 师 讲 义讲义编号: ______________ 副校长/组长签字: 签字日期:【考纲说明】1、理解平面向量的概念和几何表示,掌握向量的加、减、数乘运算及其几何意义,会用坐标表示.2、了解平面向量的基本定理,掌握平面向量的坐标运算.3、本部分在高考中占5分.【趣味链接】1、向量最初被应用于物理学,被称之为矢量。
很多物理量,如力、速度、位移、电场强度、磁场强度等都是向量.2、大约公元前350年,古希腊著名学者亚里士多德就知道了力可以表示为向量,向量一词来自力学、解析几何中的有向线段.3、大陆与台湾在2008年12月25日开通了直航,在此之前乘飞机要先从台北到香港,再从香港到上海,这里发生了两次位移.【知识梳理】一、 向量的基本概念与线性运算 1、向量的概念(1)向量:既有大小又有方向的量,记作AB ;向量的大小即向量的模(长度),记作|AB|,向量不能比较大小,但向量的模可以比较大小.(2)零向量:长度为0的向量,记为0 ,其方向是任意的,0与任意向量平行.(3)单位向量:模为1个单位长度的向量,常用e 表示.(4)平行向量(共线向量):方向相同或相反的非零向量,记作a ∥b,平行向量也称为共线向量(5)相等向量:长度相等且方向相同的向量,相等向量经过平移后总可以重合,记为b a=,大小相等,方向相同),(),(2211y x y x =⎩⎨⎧==⇔2121y y x x .(6)相反向量:与a 长度相等、方向相反的向量,叫做a 的相反向量.记作a-,零向量的相反向量仍是零向量.若a 、b是互为相反向量,则a =b -,b =a -,a +b =0 .2、向量的线性运算(1)向量的加法:求两个向量和的运算叫做向量的加法.向量加法满足交换律与结合律;向量加法有“三角形法则”与“平行四边形法则”.(2)向量的减法 :求向量a 加上b 的相反向量的运算叫做a 与b的差.向量的减法有三角形法则,b a -可以表示为从b 的终点指向a 的终点的向量(a 、b有共同起点).(3)向量的数乘运算:求实数λ与向量a 的积的运算,记作λa.①a a ⋅=λλ;②当0>λ时,λa 的方向与a 的方向相同;当0<λ时,λa 的方向与a的方向相反; 当0=λ时,0 =a λ,方向是任意的.③数乘向量满足交换律、结合律与分配律. 二、平面向量的基本定理与坐标表示 1、平面向量的基本定理如果21,e e 是一个平面内的两个不共线向量,那么对这一平面内的任一向量a,有且只有一对实数21,λλ使:2211e e a λλ+=,其中不共线的向量21,e e叫做表示这一平面内所有向量的一组基底.2、平面向量的坐标表示(1)在直角坐标系中,分别取与x 轴、y 轴方向相同的两个单位向量,i j作为基底. 由平面向量的基本定理知,该平面内的任一向量a 可表示成a xi yj =+ ,由于a 与数对(x,y)是一一对应的,因此把(x,y)叫做向量a的坐标,记作a =(x,y),其中x 叫作a在x 轴上的坐标,y 叫做在y 轴上的坐标.显然0 =(0,0),(1,0)i = ,(0,1)j =.(2)设OA xi y j =+.则向量OA 的坐标(x,y)就是终点A 的坐标,即若OA =(x,y),则A 点的坐标为(x,y),反之亦成立ECBA(O 是坐标原点). 3、平面向量的坐标运算(1)若()()1122,,,a x y b x y == ,则()1212,a b x x y y ±=±±.(2)若()()2211,,,y x B y x A ,则()2121,AB x x y y =-- ,AB =(3)若a =(x,y),则λa=(λx, λy).(4)若()()1122,,,a x y b x y == ,则1221//0a b x y x y ⇔-=. (5)若()()1122,,,a x y b x y == ,则1212a b x x y y ⋅=⋅+⋅.【经典例题】【例1】(2010全国)△ABC 中,点D 在边AB 上,CD 平分∠ACB ,若CB a =,CA b =,1,2a b ==,则CD =( ) A.1233a b +B.2133a b +C.3455a b +D.4355a b + 【例2】(2009湖南)如图,D ,E ,F 分别是∆ABC 的边AB ,BC ,CA 的中点,则( )A .0AD BE CF ++=B .0BD CF DF -+=C .0AD CE CF +-= D .0BD BE FC --=【例3】(2009全国)设非零向量a 、b 、c 满足c b a c b a =+==|,|||||,则>=<b a , ( )A .150° B.120° C.60° D.30°【例4】(2012辽宁)已知两个非零向量a ,b 满足|a +b |=|a -b |,则下面结论正确的是( ) A .a ∥b B .a ⊥b C .{0,1,3} D .a +b =a -b【例5】(2009广东)已知平面向量a =,1x (),b =2,x x (-),则向量+a b ( )A. 平行于x 轴B. 平行于第一、三象限的角平分线C. 平行于y 轴D. 平行于第二、四象限的角平分线【例6】(2012浙江)设a ,b 是两个非零向量,以下说法正确的是( )A .若|a +b |=|a |-|b |,则a ⊥bB .若a ⊥b ,则|a +b |=|a |-|b |C .若|a +b |=|a |-|b |,则存在实数λ,使得a =λbD .若存在实数λ,使得a =λb ,则|a +b |=|a |-|b |【例7】若向量,2,()a b a b a b a ==-⊥满足,则向量b a 与的夹角等于 .【例8】已知平面上的向量PA 、PB满足224PA PB += ,2AB = ,设向量2PC PA PB =+ ,则PC 的最小值是 .【例9】(2009湖南)已知向量(sin ,cos 2sin ),(1,2).a b θθθ=-=(1)若//a b ,求tan θ的值;(2)若||||,0,a b θπ=<< 求θ的值。
高中数学必修二第六章平面向量及其应用必考知识点归纳(带答案)

高中数学必修二第六章平面向量及其应用必考知识点归纳单选题1、已知向量a⃑=(1,−√7),|b⃑⃑|=3,a⃑⋅b⃑⃑=3√6,则a⃑与b⃑⃑的夹角为()A.π6B.π4C.π3D.2π3答案:A分析:先计算向量a⃑的模,再根据向量数量积的定义,将a⃑⋅b⃑⃑=3√6展开,即可求得答案. 因为a⃑=(1,−√7),所以|a⃑|=√12+(−√7)2=2√2,又因为a⃑⋅b⃑⃑=3√6,设a⃑与b⃑⃑的夹角为θ,θ∈[0,π],所以|a⃑||b⃑⃑|cosθ=3√6,即2√2×3×cosθ=3√6,解得cosθ=√32,故θ=π6,故选:A.2、在△ABC中,角A,B,C的对边分别为a,b,c,且B=π3,b=3,a=√3,则c=().A.√3B.2√3C.3−√3D.3答案:B分析:利用余弦定理可构造方程直接求得结果.在△ABC中,由余弦定理得:b2=a2+c2−2accosB=3+c2−√3c=9,即c2−√3c−6=0,解得:c=2√3或c=−√3(舍),∴c=2√3.故选:B.3、已知向量a⃑与b⃑⃑的夹角为π6,且|a⃑|=2|b⃑⃑|=2,则a⃑⋅b⃑⃑=()A.√3B.1C.2√3D.2答案:A解析:利用向量数量积的定义即可求解.由|a⃑|=2|b⃑⃑|=2,则|a⃑|=2,|b⃑⃑|=1,又向量a⃑与b⃑⃑的夹角为π6,所以a⃑⋅b⃑⃑=|a⃑||b⃑⃑|cos⟨a⃑,b⃑⃑⟩=2×1×√32=√3.故选:A小提示:本题考查了向量数量积的定义,考查了基本运算求解能力,属于基础题.4、已知向量a⃗=(√3,1),b⃑⃗=(−√3,1),则a⃗与b⃑⃗的夹角为()A.30°B.60°C.120°D.150°答案:C分析:根据数量积的夹角公式进行求解,再结合平面向量夹角范围即可得到答案解:cos⟨a⃗,b⃑⃑⟩=a⃑⃗⋅b⃑⃑|a⃑⃗||b⃑⃑|=−3+12×2=−12,因为0°≤⟨a⃗,b⃑⃑⟩≤180°,所以⟨a⃗,b⃑⃑⟩=120°,故选:C5、△ABC的内角A、B、C的对边分别为a、b、c,C=30∘,c=10.如果△ABC有两解,则a的取值范围是()A.[10,20]B.[10,10√3]C.(10,10√3)D.(10,20)答案:D分析:作出图形,根据题意可得出关于a的不等式,由此可解得a的取值范围.如下图所示:因为△ABC有两解,所以asinC=12a<c=10<a,解得10<a<20.故选:D.6、如图,△ABC中,角C的平分线CD交边AB于点D,∠A=2π3,AC=2√3,CD=3√2,则BC=()A.3√3B.4C.4√2D.6答案:D分析:△ACD中由正弦定理求得∠ADC后可得∠ACD,从而得∠ACB,B角,得AB,用余弦定理可得BC.在△ACD中,根据正弦定理得sin∠ADC=AC⋅sinACD =2√3×√323√2=√22,由∠ADC<∠A,所以∠ADC=π4,所以∠ACD=π−2π3−π4=π12,所以∠ACB=π6,则∠B=π6,所以AB=AC=2√3,在△ABC中,由余弦定理得BC2=(2√3)2+(2√3)2−2×2√3×2√3×(−12)=36,所以BC=6.故选:D.小提示:关键点点睛:本题主要考查正弦定理,余弦定理,特殊角的三角函数值等基础知识,解题时对照已知条件选用恰当的公式进行计算.如先在△ACD中选用正弦定理求得两边中另一边的对角,可得三角形的第三角,这样图形听所有角都已知,然后再求选用公式求边.本题也可以不用余弦定理求边BC.7、如图,四边形ABCD是平行四边形,则12AC⃑⃑⃑⃑⃑⃑+12BD⃑⃑⃑⃑⃑⃑⃑=()A .AB ⃑⃑⃑⃑⃑⃑B .CD ⃑⃑⃑⃑⃑⃑C .CB ⃑⃑⃑⃑⃑⃑D .AD ⃑⃑⃑⃑⃑⃑ 答案:D分析:由平面向量的加减法法则进行计算. 由题意得AC ⃑⃑⃑⃑⃑⃑=AB ⃑⃑⃑⃑⃑⃑+AD ⃑⃑⃑⃑⃑⃑,BD ⃑⃑⃑⃑⃑⃑⃑=AD ⃑⃑⃑⃑⃑⃑−AB⃑⃑⃑⃑⃑⃑, 所以12AC ⃑⃑⃑⃑⃑⃑+12BD ⃑⃑⃑⃑⃑⃑⃑=12(AB ⃑⃑⃑⃑⃑⃑+AD ⃑⃑⃑⃑⃑⃑+AD ⃑⃑⃑⃑⃑⃑−AB ⃑⃑⃑⃑⃑⃑)=AD ⃑⃑⃑⃑⃑⃑.故选:D.8、若|AB ⃑⃑⃑⃑⃑⃑|=5,|AC ⃑⃑⃑⃑⃑⃑|=8,则|BC ⃑⃑⃑⃑⃑⃑|的取值范围是( ) A .[3,8]B .(3,8) C .[3,13]D .(3,13) 答案:C分析:利用向量模的三角不等式可求得|BC⃑⃑⃑⃑⃑⃑|的取值范围. 因为|BC ⃑⃑⃑⃑⃑⃑|=|AC ⃑⃑⃑⃑⃑⃑−AB ⃑⃑⃑⃑⃑⃑|,所以,||AC ⃑⃑⃑⃑⃑⃑|−|AB ⃑⃑⃑⃑⃑⃑||≤|BC ⃑⃑⃑⃑⃑⃑|≤|AC ⃑⃑⃑⃑⃑⃑|+|AB ⃑⃑⃑⃑⃑⃑|,即3≤|BC ⃑⃑⃑⃑⃑⃑|≤13. 故选:C. 多选题9、设△ABC 的内角A 、B 、C 所对边的长分别为a 、b 、c ,下列命题正确的是( ) A .若a 2+b 2<c 2,则C >π2B .若ab =c 2,则C ≥π3 C .若a 3+b 3=c 3,则C <π2 D .若a +b =2c ,则C >π2 答案:AC分析:利用余弦定理及基本不等式一一判断即可; 解:对于A 选项,a 2+b 2<c 2,可以得出cosC =a 2+b 2−c 22ab <0,∴C >π2,故A 正确;对于B 选项,因为ab =c 2,所以cos C =a 2+b 2−c 22ab≥2ab−ab 2ab=12,当且仅当a =b 时取等号,因为C ∈(0,π),所以0<C ≤π3,故B 错误;对于C 选项,假设C ≥π2,则c >a ,c >b ,则c 2≥a 2+b 2,所以c 3≥a 2c +b 2c >a 3+b 3与a 3+b 3=c 3矛盾,∴C <π2,故C 正确,对于D 选项,取a =b =c =2,满足a +b =2c ,此时C =π3,故D 错误;故选:AC.10、已知△ABC 中,角A 、B 、C 所对的边分别是a 、b 、c 且a =6,4sin B =5sin C ,有以下四个命题中正确命题有 ( )A .△ABC 的面积的最大值为40B .满足条件的△ABC 不可能是直角三角形 C .当A =2C 时,△ABC 的周长为15D .当A =2C 时,若O 为△ABC 的内心,则△AOB 的面积为√7 答案:ACD分析:对于A ,运用圆的方程和三角形的面积公式,即可得到所求最大值;对于B ,考虑勾股定理的逆定理,即可判断;对于C ,运用正弦定理可得4b =5c ,运用三角函数的恒等变换,即可得到所求周长;对于D ,运用正弦定理和三角函数的恒等变换、三角形的面积公式和等积法,即可得到所求面积. 以BC 的中点为坐标原点,BC 所在直线为x 轴,可得B (﹣3,0),C (3,0), 4sin B =5sin C ,可得4b =5c ,设A (m ,n ),可得4√(m −3)2+n 2=5√(m +3)2+n 2,平方可得16(m 2+n 2﹣6m +9)=25(m 2+n 2+6m +9), 即有m 2+n 2+823m +9=0,化为(m +413)2+n 2=(403)2,则A 的轨迹为以(﹣413,0),半径为403的圆,可得△ABC 的面积的最大值为12×6×403=40, 故A 对;a =6,4sin B =5sin C 即4b =5c ,设b =5t ,c =4t ,由36+16t 2=25t 2,可得t =43,满足条件的△ABC 可能是直角三角形,故B 错误;a =6,4sin B =5sin C ,A =2C ,可得B =π﹣3C ,由正弦定理可得4b =5c ,可得b =5c4,由b sinB =csinC ,可得5c 4sin(π−3C)=csinC =5c 4sinC (4cos 2C−1),由sin C ≠0,可得:4cos 2C ﹣1=54,解得:cos C =34,或﹣34(舍去),sin C =√1−cos 2C =√74,可得sin A =2sin C cos C =2×34×√74=3√78, 3√78=√74,可得:c =4,b =5,则a +b +c =15,故C 对;a =6,4sin B =5sin C ,A =2C ,可得B =π﹣3C ,由正弦定理可得4b =5c ,可得b =5c4,由b sinB=csinC,可得5c 4sin(π−3C)=csinC =5c 4sinC (4cos 2C−1),由sin C ≠0,可得:4cos 2C ﹣1=54,解得:cos C =34,或﹣34(舍去), sin C =√1−cos 2C =√74,可得:sin A =2sin C cos C =2×34×√74=3√78, 3√78=c √74,可得:c =4,b =5,S △ABC =12bc sin A =12×5×4×3√78=15√74. 设△ABC 的内切圆半径为R ,则R =2Sa+b+c=2×15√744+5+6=√72,S △ABO =12cR =12×4×√72=√7.故D 对.故选:ACD .小提示:本题考查三角形的正弦定理和面积公式的运用,考查三角函数的恒等变换,考查转化思想和运算能力,属于难题.11、已知向量a ⃑=(2,1),b ⃑⃑=(−3,1),则( ) A .(a ⃑+b ⃑⃑)⊥a ⃑B .|a ⃑+2b⃑⃑|=6 C .向量a ⃑在向量b ⃑⃑上的投影向量是(−65,25)D .(2√55,√55)是向量a ⃑的单位向量答案:AD分析:根据向量坐标的线性运算及数量积的坐标运算即可判断判断A ; 根据向量坐标的线性运算及向量的模的坐标运算即可判断判断B ; 根据投影向量的计算公式即可判断C ; 判断向量(2√55,√55)是否与向量a ⃑共线,及模是否为1,即可判断D.解:对于A ,a ⃑+b ⃑⃑=(−1,2),则(a ⃑+b ⃑⃑)⋅a ⃑=−2+2=0, 所以(a ⃑+b ⃑⃑)⊥a ⃑,故A 正确;对于B ,a ⃑+2b ⃑⃑=(−4,3),则|a ⃑+2b ⃑⃑|=5,故B 错误; 对于C ,向量a ⃑在向量b ⃑⃑上的投影向量为|a ⃑|⋅cos⟨a ⃑,b ⃑⃑⟩⋅b⃑⃑|b⃑⃑|=a⃑⃑⋅b ⃑⃑|b⃑⃑|⋅b⃑⃑|b⃑⃑|=−5b ⃑⃑10=(32,−12),故C 错误; 对于D ,因为向量(2√55,√55)的模等于1,2√55×1−2×√55=0,所以向量(2√55,√55)与向量a ⃑共线,故(2√55,√55)是向量a ⃑的单位向量,故D 正确.故选:AD. 填空题12、骑自行车是一种能有效改善心肺功能的耐力性有氧运动,深受大众喜爱,如图是某一自行车的平面结构示意图,已知图中的圆A (前轮),圆D (后轮)的半径均为√3,△ABE ,△BEC ,△ECD 均是边长为4的等边三角形,设点P 为后轮上的一点,则在骑动该自行车的过程中,AC⃑⃑⃑⃑⃑⃑⋅BP ⃑⃑⃑⃑⃑⃑的最大值为___________.答案:36分析:由题意以AD 所在的直线为x 轴,以点D 为坐标原点建立平面直角坐标系,将所涉及的点的坐标求出,其中P 点坐标借助于三角函数表示,则所求的结果即可转化为三角函数的最值问题求解.由题意圆D (后轮)的半径均为√3,△ABE ,△BEC ,△ECD 均是边长为4的等边三角形,点P 为后轮上的一点,如图以AD 所在的直线为x 轴,以点D 为坐标原点建立平面直角坐标系:则A (−8,0),B(−6,2√3),C(−2,2√3).圆D 的方程为x 2+y 2=3,设P(√3cosα,√3sinα), 所以AC⃑⃑⃑⃑⃑⃑=(6,2√3),BP ⃑⃑⃑⃑⃑⃑=(√3cosα+6,√3sinα−2√3), 故AC⃑⃑⃑⃑⃑⃑⋅BP ⃑⃑⃑⃑⃑⃑=6sinα+6√3cosα+24=12sin (α+π3)+24≤12+24=36. 所以答案是:36.13、海伦公式是利用三角形的三条边的边长a ,b ,c 直接求三角形面积S 的公式,表达式为:S =√p(p −a)(p −b)(p −c),p =a+b+c 2;它的特点是形式漂亮,便于记忆.中国宋代的数学家秦九韶在1247年独立提出了“三斜求积术”,虽然它与海伦公式形式上有所不同,但它与海伦公式完全等价,因此海伦公式又译作海伦-秦九韶公式.现在有周长为10+2√7的△ABC 满足sinA:sinB:sinC =2:3:√7,则用以上给出的公式求得△ABC 的面积为___________. 答案:6√3分析:由正弦定理得三角形三边之比,由周长求出三边,代入公式即可. ∵sinA:sinB:sinC =2:3:√7,∴a:b:c =2:3:√7, ∴△ABC 周长为10+2√7,即a +b +c =10+2√7, ∴a =4,b =6,c =2√7,∴p =4+6+2√72=5+√7,∴△ABC 的面积S =√(5+√7)(1+√7)(√7−1)(5−√7)=6√3. 所以答案是:6√3.14、已知P ,Q 分别是四边形ABCD 的对角线AC 与BD 的中点,BC ⃑⃑⃑⃑⃑⃑=a ⃑,DA ⃑⃑⃑⃑⃑⃑=b ⃑⃑,且a ⃑,b ⃑⃑是不共线的向量,则向量PQ⃑⃑⃑⃑⃑⃑=___________. 答案:−12a ⃑−12b⃑⃑ 分析:取AB 的中点E ,连接PE,QE ,然后利用向量的加法法则和三角形中位线定理求解. 如图,取AB 的中点E ,连接PE,QE ,因为P ,Q 分别是四边形ABCD 的对角线AC 与BD 的中点,BC ⃑⃑⃑⃑⃑⃑=a ⃑,DA ⃑⃑⃑⃑⃑⃑=b⃑⃑ 所以PE ⃑⃑⃑⃑⃑⃑=12CB ⃑⃑⃑⃑⃑⃑=−12a ⃑,EQ ⃑⃑⃑⃑⃑⃑=12AD ⃑⃑⃑⃑⃑⃑=−12b⃑⃑, 所以PQ ⃑⃑⃑⃑⃑⃑=PE ⃑⃑⃑⃑⃑⃑+EQ ⃑⃑⃑⃑⃑⃑=12CB ⃑⃑⃑⃑⃑⃑+12AD ⃑⃑⃑⃑⃑⃑=−12a ⃑−12b⃑⃑. 所以答案是:−12a ⃑−12b⃑⃑解答题15、已知向量a ⃑与b ⃑⃑的夹角为120∘,|a ⃑|=3,|b ⃑⃑|=2. (1)求(2a ⃑+b ⃑⃑)⋅(a ⃑−2b ⃑⃑)的值; (2)求|2a ⃑+b ⃑⃑|的值. 答案:(1)19;(2)2√7.分析:(1)由向量数量积的定义计算即可求解; (2)先计算|2a ⃑+b ⃑⃑|2=(2a ⃑+b ⃑⃑)2的值,再开方即可求解. (1)因为|a ⃑|=3,|b ⃑⃑|=2,且a ⃑,b ⃑⃑的夹角为120∘, 所以a ⃑⋅b ⃑⃑=|a ⃑|⋅|b⃑⃑|⋅cos120∘=3×2×(−12)=−3, 所以(2a ⃑+b ⃑⃑)⋅(a ⃑−2b ⃑⃑)=2a ⃑2−3a ⃑⋅b⃑⃑−2b ⃑⃑2=2|a⃑|2−3a⃑⋅b⃑⃑−2|b⃑⃑|2=2×9−3×(−3)−2×4=19;(2)|2a⃑+b⃑⃑|2=(2a⃑+b⃑⃑)2=4|a⃑|2+4a⃑⋅b⃑⃑+|b⃑⃑|2=36−12+4=28,所以|2a⃑+b⃑⃑|=2√7.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
向量加减混合运算(北京习题集)(教师版)一.选择题(共5小题)1.(2020春•海淀区校级期中)下列说法错误的是( )A .若OD OE OM +=,则OM OE OD -=B .若OD OE OM +=,则OM DO OE +=C .若OD OE OM +=,则OD EO OM -= D .若OD OE OM +=,则DO EO OM +=2.(2008秋•怀柔区期末)O 、A 、B 、C 为空间四边形四个顶点,点M 、N 分别是边OA 、BC 的中点,且OA a =,OB b =,OC c =,用a ,b ,c 表示向量MN 为( )A .1()2a c b +-B .1()2a b c +-C .1()2c b a +-D .1()2a b c ++ 3.(2008•怀柔区模拟)1(26)32a b b +-等于( ) A .2a b - B .a b - C .a D .b 4.(2008•怀柔区模拟)如图,D 、E 、F 分别是ABC ∆三边的中点,则下列等式中正确的是( )A .FD DA FA +=B .0FD DE FE ++=C .DE DA EB +=D .DA DE FD +=5.(2007•东城区二模)已知向量(3a =,4-),(5,2)b =,则向量a b +等于( )A .(2,6)B .(6,2)C .(8,2)-D .(8,2)-二.填空题(共3小题)6.(2019秋•石景山区期末)在平行四边形ABCD 中,已知向量(1,2)AB =,(2,3)AD =,则AC = .7.(2007秋•朝阳区期末)在矩形ABCD 中,E 是CD 的中点,AB a =,AD b =,用a 、b 表示BE 为8.(2015•丰台区二模)已知梯形ABCD 中,12AD DC CB AB ===,P 是BC 边上一点,且AP xAB y AD =+.当P 是BC 中点时,x y += ;当P 在BC 边上运动时,x y +的最大值是 .向量加减混合运算(北京习题集)(教师版)参考答案与试题解析一.选择题(共5小题)1.(2020春•海淀区校级期中)下列说法错误的是( )A .若OD OE OM +=,则OM OE OD -=B .若OD OE OM +=,则OM DO OE +=C .若OD OE OM +=,则OD EO OM -= D .若OD OE OM +=,则DO EO OM +=【分析】根据向量的加法、减法运算,及相反向量的概念进行判断即可.【解答】解:若OD OE OM +=,①则OM OE OD -=,A 正确;②则OM OD OE -=;∴OM DO OE +=,B 正确;③则OD EO OM -=,C 正确;④则DO EO MO +=,D 错误.故选:D .【点评】考查向量的加法、减法运算,向量的数乘运算,相反向量的概念.2.(2008秋•怀柔区期末)O 、A 、B 、C 为空间四边形四个顶点,点M 、N 分别是边OA 、BC 的中点,且OA a =,OB b =,OC c =,用a ,b ,c 表示向量MN 为( )A .1()2a c b +-B .1()2a b c +-C .1()2c b a +-D .1()2a b c ++ 【分析】由题意,O 、A 、B 、C 为空间四边形四个顶点,点M 、N 分别是边OA 、BC 的中点,由用向量的加法法则可以得出MN MA AB BN =++,根据图形用a ,b ,c 表示出再对照四个选项得出正确答案【解答】解:如图MN MA AB BN =++又点M 、N 分别是边OA 、BC 的中点∴MN MA AB BN =++12OA AB BN =++ 1122OA OB OA BC =+-+11()22OA OB OA OC OB =+-+⨯- 111222OA OB OC =-++ 又OA a =,OB b =,OC c =,∴1()2MN c b a =+- 故选:C .【点评】本题考查向量的加减运算及其几何意义,解题的关键是作出图象由向量的线性运算规则用三个向量表示出向量MN3.(2008•怀柔区模拟)1(26)32a b b +-等于( ) A .2a b - B .a b - C .a D .b【分析】根据两个向量的加减法的法则,以及其几何意义可得1(26)3332a b b a b b a +-=+-=. 【解答】解:1(26)3332a b b a b b a +-=+-=,故选C . 【点评】本题考查两个向量的加减法的法则,以及其几何意义,属于容易题.4.(2008•怀柔区模拟)如图,D 、E 、F 分别是ABC ∆三边的中点,则下列等式中正确的是( )A .FD DA FA +=B .0FD DE FE ++=C .DE DA EB +=D .DA DE FD +=【分析】由向量加法的三角形法则知选项A 正确.选项B 不正确,由三角形的中位线性质得选项C 不正确,由 DE DA EC DF FD +==≠,可知选项D 不正确.【解答】解:由向量加法的法则得FD DA FA +=,故选项A 正确2FD DE FE FE ++=,选项B 不正确. D 、E 、F 分别是ABC ∆的边AB 、BC 、CA 的中点,∴DE DA DE EF DF BE +=+==,故选项C 不正确.由上知 DE DA EC DF FD +==≠,故选项D 不正确,故选:A .【点评】本题考查两个向量加法的法则及几何意义,三角形的中位线的性质,属于基础题.5.(2007•东城区二模)已知向量(3a =,4-),(5,2)b =,则向量a b +等于( )A .(2,6)B .(6,2)C .(8,2)-D .(8,2)-【分析】利用两个向量的坐标形式的加法法则,两个向量相加,把他们的横坐标和纵坐标分别相加.【解答】解:(3a =,4-),(5,2)b =,∴(3a b +=,4)(5-+,2)(8=,2-),故选:C .【点评】本题考查两个向量的坐标运算,两个向量和的坐标,等于这两个向量的对应坐标的和.二.填空题(共3小题)6.(2019秋•石景山区期末)在平行四边形ABCD 中,已知向量(1,2)AB =,(2,3)AD =,则AC = (3,5) .【分析】利用斜率平行四边形法则可得:AC AB AD =+,即可得出.【解答】解:在平行四边形ABCD 中,因为向量(1,2)AB =,(2,3)AD =,所以:(3,5)AC AB AD =+=.故答案为:(3,5).【点评】本题考查了向量平行四边形法则、向量坐标运算性质,考查了推理能力与计算能力,属于基础题.7.(2007秋•朝阳区期末)在矩形ABCD 中,E 是CD 的中点,AB a =,AD b =,用a 、b 表示BE 为 12BE b a =- 【分析】画出矩形ABCD ,由题意直接表示BE .【解答】解:如图11 22BE BC CE AD AB b a=+=-=-,故答案为:12b a-.【点评】本题考查向量加减混合运算及其几何意义,是基础题.8.(2015•丰台区二模)已知梯形ABCD中,12AD DC CB AB===,P是BC边上一点,且AP xAB y AD=+.当P 是BC中点时,x y+=54;当P在BC边上运动时,x y+的最大值是.【分析】①以AB为x轴,过点A与AB垂直的直线为y轴,建立平面直角坐标系,设2AB=,用向量表示AP、AB与AD,根据AP xAB y AD=+,列出方程组,求出x、y的值;②求出线段BC的方程,设出点P的坐标,利用①的方法即可求出x y+的最大值.【解答】解:①以AB为x轴,过点A与AB垂直的直线为y轴,建立平面直角坐标系,如图所示;设2AB=,则1AD DC CB===,且//DC AB,60BAD∴∠=︒;(0,0)A∴,(2,0)B,3(2C3,1(2D3;BC∴的中点7(4P3),∴7(4AP=3),(2,0)AB=,1(2AD=3,AP xAB y AD=+,7(4∴3(2x=,10)(2y+31)(22x y=+3)y,∴1722433x yy⎧+=⎪⎪⎨⎪=⎪,解得34x=,12y=;315424x y∴+=+=;②线段BC的方程为3(2)y x=--,3([2x∈,2]),设点0(P x ,03(2))x --,03[2x ∈,2], ∴0(AP x =,03(2))x --,1(22AP xAB yAD x y =+=+,3)y , ∴0012233(2)x y x y x ⎧+=⎪⎪⎨⎪=--⎪,解得01x x =-,024y x =-+;03x y x ∴+=-+,03[2x ∈,2],∴当32x =时,33322x y +=-+=为最大值. 故答案为:54,32.【点评】本题考查了直线方程的应用问题,也考查了平面向量的坐标运算问题,解题的关键是建立适当的平面直角坐标系,并把向量进行坐标表示,是综合性题目.。
