用“调整优值法”求“线性规划问题”的最优整数解
线性规划中的最优整数解
线性规划中的最优整数解线性规划中的最优解,就是在线性约束条件下使目标函数取得最大值或最小值的可行解,而求最优整数解,是同学们的棘手问题,下面以例题的形式讲讲如何求最优解。
例. 某人承揽了一项业务:需做文字标牌6个,绘画标牌5个。
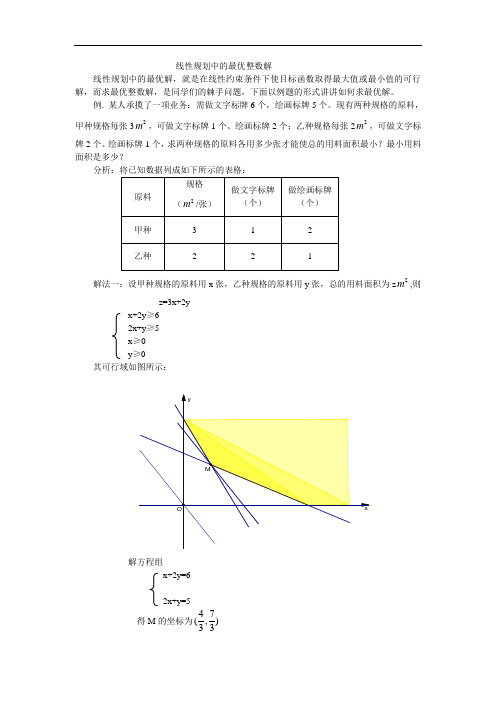
现有两种规格的原料,甲种规格每张32m ,可做文字标牌1个、绘画标牌2个;乙种规格每张22m ,可做文字标牌2个、绘画标牌1个,求两种规格的原料各用多少张才能使总的用料面积最小?最小用料面积是多少?分析:将已知数据列成如下所示的表格:解法一:设甲种规格的原料用x 张,乙种规格的原料用y 张,总的用料面积为z 2m ,则z=3x+2yx+2y ≥62x+y ≥5x ≥0y ≥0其可行域如图所示:解方程组x+2y=62x+y=5得M 的坐标为47(,)33当直线z=3x+2y过点M47(,)33时z最小,此时472632333z=⨯+⨯=由题意可知,点M47(,)33不是最优解,因为此问题最优解(x,y)中x,y应都是非负整数,所以目标函数z的最小值一定是大于263的整数,且x,y都是非负整数。
取z=9,得3x+2y=9,其非负整数解是(1,3)和(3,0),但点(3,0)不在可行域内,舍去,所以点(1,3)是最优解,min 9z=解法二:由解法一可知,点M47(,)33不是最优解,这时可求出可行域内左下侧靠近边界的整点,依次为A(0,5),B(1,3),C(2,2),D(3,2),E(4,1),F(5,1),G(6,0),将这些点的坐标分别代入目标函数z=3x+2y,求出z的各对应值,经检验可知,在整点B(1,3)处z取得最小值9。
答:甲种规格的原料用1张,乙种规格的原料用3张时,总的用料面积最小,其最小用料面积为92m。
对于线性规划中的最优整数解问题,当解方程组得到的解不是整数解时,可采用如下的方法:1.调整优值法:先求“非整点最优解”及“最优值”,根据题意调整“最优值”,再求目标函数中的整数解,便可得出最优整数解。
人教版高中数学必修5第三章不等式 3.3.2 简单的线性规划问题

钢板张数最少?
分
A规格 B规格 C规格 张数
析: 第一种钢板
2
1
1
x
列 第二种钢板
1
2
3
y
表 成品块数 2x y x 2y x 3y
解:设需截第一种钢板x张,第二种钢板y张,共需截
这两种钢板共z张,则
2x y 15,
x x
2y 3y
18, 27,
x 0,
分析:对应无数个点,即直线与边界线重合时. 作出可行域,结合图形,看直线 l : y ax z
与哪条边界线重合时,可取得最大值.
解:当直线 l : y ax z 与边界
线重合时,有无数个点,
使函数值取得最大值,
此时有 kl kAC .
3
3
k AC
5
, kl
a
ห้องสมุดไป่ตู้. 5
问题的最优解.
(1)在上述问题中,如果每生产一件甲产品
获利3万元,每生产一件乙产品获利2万元,
又当如何安排生产才能获得最大利润?
(2)由上述过程,你能得出最优解与可行域之间的关 系吗?
设生产甲产品x件乙产品y件时,工厂获得的利润为
z,则z=3x+2y.
把z 3x 2 y变形为y 3 x z ,这是斜率为 3 ,
利用平移的方法找出与可行域有公共点 且纵截距最大或最小的直线;
(3)求:通过解方程组求出最优解; (4)答:作出答案. 最优解一般在可行域的顶点处取得.
x 4 y 3, 例2 已知x, y满足 3x 5 y 25,设z ax y(a 0),
求线性规划问题的最优整数解的方法

求线性规划问题的最优整数解的方法作者:陈树礼来源:《中学教学参考·理科版》2010年第01期线性规划是新教材新增内容,在近几年高考中都以较易题目出现,要学好本节内容,应注意以下三点.一、判定最优解求线性目标函数z=ax+by(a≠0、b≠0)在线性约束条件下的最优解问题,可转化为求直线y=-abx+zb在y轴上的截距的最大值和最小值.易知在b>0时,当zb最大时,z取得最大值,当zb最小时,z取得最小值;在b二、求出最优解依据边界直线的斜率(或倾斜角)计算出最优解.三、修正最优解,得到最优整数解现改编人教版高二(上例3的问题,以求达到抛砖引玉的目的.【例】某工厂生产甲、乙两种产品.已恬生产甲种产品1t需耗A种矿石10t、B种矿石5t、煤4t;生产乙种产品1t需耗A种矿石4t、B种矿石4t、煤9t.每1t甲种产品的利润是600元,每1t乙种产品的利润是1000元.工厂在生产这两种产品的计划中要求消耗A种矿石不超过300t、B种矿石不超过200t、煤不超过360t.求:(1)甲、乙两种产品各生产多少吨(精确到1吨)才能使利润最大?(2)若甲种产品每吨利润600元,乙产品每吨利润200元.甲、乙两种产品各生产多少吨(精确到1吨)才能使利润最大?(3)若甲种产品每吨利润400元,乙产品每吨利润200元.甲、乙两种产品各生产多少吨(精确到1吨)才能使利润最大?(4)若甲种产品每吨利润200元,乙产品每吨利润600元.甲、乙两种产品各生产多少吨(精确到1吨)才能使利润最大?(5)若甲种产品每吨利润1000元,乙产品每吨利润800元.甲、乙两种产品各生产多少吨(精确到1吨)才能使利润最大?解:(1)设生产甲、乙两种产品分别为x吨,y吨.利润为z元.则10x+4y≤300,5x+4y≤200,4x+9y≤360,x≥0,y≥0,z=600x+1000y.作出以上不等式组表示的平面区域,即可行域.作直线:600x+1000y=0,即直线:3x+5y=0,则z=200(3x+5y).设u=3x+5y,则当u最大时,z最大.易知直线NQ、MN、PM的斜率分别为-52,-54,-49,直线l的斜率为-53.平移直线∵M点为最优解点.由方程组5x+4y=200,4x+9y=360得M点的坐标为(36029,100029).∵x,y都是正整数,∴u=3x+5y=608029也应为正整数.∴u=3x+5y≤209.于是整点(11,35)为所求.当生产甲产品11吨,乙产品35吨时,能使利润总额最大.(2)此时目标函数为z=600x+200y.作直线平移直线∵直线经过点Q(30,0)时,z取得最大值.即只生产甲产品30吨时,获得利润最大.(3)此时目标函数为z=400x+200y.作直线平移直线∵-类似(1)可求解.(4)此时目标函数为z=200x+600y.作直线平移直线∵--49.∴当直线经过点P(0,40)时,5x+4y=0,即只生产乙产品40吨时,获得利润最大.(5)此时目标函数为z=1000x+800y.作直线平移直线∵-∴当直线与直线5x+4y=0重合时,z取得最大值.∴当点位于线段MN上任意一点时,都能使z取得最大值.总之,在本部分内容的学习中,要做到“一定、二算、三修正”.(责任编辑金铃)。
线性规划的解与最优解知识点总结

线性规划的解与最优解知识点总结在现实生活和工作中,我们经常会遇到需要最优化某个目标函数的问题。
线性规划作为一种常见的数学优化方法,在各个领域中得到了广泛应用。
它能够帮助我们在一定的约束条件下,找到目标函数的最佳解。
本文将对线性规划的解与最优解的相关知识点进行总结。
1. 基本概念线性规划问题由目标函数和一组线性约束条件组成。
目标函数的形式通常是最大化或最小化一些变量的线性组合,而约束条件则给出了这些变量的取值范围。
线性规划问题的一般形式如下:```max/min Z = c₁x₁ + c₂x₂ + ... + cₙxₙsubject to:a₁₁x₁ + a₁₂x₂ + ... + a₁ₙxₙ ≤ b₁...aₙ₁x₁ + aₙ₂x₂ + ... + aₙₙxₙ ≤ bₙx₁, x₂, ..., xₙ ≥ 0```其中,Z表示目标函数的值,c₁, c₂, ..., cₙ为目标函数的系数,aᵢₙ为约束条件中的系数,b₁, b₂, ..., bₙ为约束条件的右边常数,x₁,x₂, ..., xₙ为决策变量。
2. 解的存在性线性规划问题存在三种解的情况:无解、有界解和无界解。
如果约束条件与目标函数之间存在矛盾,例如出现一个约束条件为 a₁₁x₁ +a₁₂x₂ + ... + a₁ₙxₙ ≤ b₁,而目标函数的系数为 c₁ > a₁₁,那么这个线性规划问题就没有解。
有界解指的是线性规划问题在满足所有约束条件的情况下,能够找到目标函数的最大值或最小值。
无界解意味着目标函数可以无限制地增大或减小。
3. 最优解的性质线性规划问题的最优解具有以下性质:- 最优解必然出现在可行域的顶点上。
可行域是指所有满足约束条件的解的集合,而顶点则指可行域的边界上的点。
- 如果最优解存在,那么至少存在一个顶点是最优解。
- 如果可行域是有限的,则一定存在一个顶点是最优解。
- 如果最优解存在,那么一定有一条或多条约束条件在最优解上取等号。
2017届高考数学大一轮 第六章 不等式与推理证明 第3课时 二元一次不等式(组)与简单的线性规划问题 理

1.(2015·高考陕西卷)某企业生产甲、乙两种产品均需用A,
B两种原料.已知生产1吨每种产品所需原料及每天原料的可用限
额如表所示.如果生产1吨甲、乙产品可获利润分别为3万元、4
万元,则该企业每天可获得最大利润为( )
A.12万元
A(吨) B(吨)
甲 乙 原料限额
32
12
12
8
B.16万元
C.17万元
主干回顾 夯基固源 考点研析 题组冲关 素能提升 学科培优
课时规范训练
第3课时 二元一次不等式(组)与简单的线性规划问题
1.会从实际情境中抽象出二元一次不等式组. 2.了解二元一次不等式的几何意义,能用平面区域表示二 元一次不等式组. 3.会从实际情境中抽象出一些简单的二元线性规划问题, 并能加以解决.
1.(2015·高考湖南卷)若变量x,y满足约束条件
x2+x-y≥y≤-11,, 则z=3x-y的最小值为(
)
y≤1.
A.-7 C.1
B.-1 D.2
解析:画出可行域,如图中阴影部分所示.目标函数z=3x-
y可化为y=3x-z,其斜率为3,纵截距为-z,平移直线y=3x知
当直线y=3x-z经过点A时,其纵截距最大,z取得最小值.由
1.二元一次不等式表示的平面区域 (1)一般地,二元一次不等式Ax+By+C>0在平面直角坐标 系中表示直线Ax+By+C=0某一侧的所有的点组成的平面区域 (半平面) 不含 边界直线,不等式Ax+By+C≥0所表示的平 面区域(半平面)含有边界直线.
(2)对于直线Ax+By+C=0同一侧的所有的点(x,y),使得Ax
解析 当m≥0时,若平面区域存在,则平面区域内的点在第 二象限,平面区域内不可能存在点P(x0,y0)满足x0-2y0=2,因此 m<0.
如何寻找_线性规划问题_的整点最优解

- 2 0 1 2 3 4 5 6 7 8 9 10 11 12
x
图1
作出一组平行的直线 200x + 150y = t. 当 t= 0 时, 即 200x + 150y = 0 也就是直线
l0: 4x + 3y = 0. 将直线 l0 向上平移至 l1 的位置时, 直线 l1 经
过可行域上的点A , 且与原点的距离最大, 此时 z = 200x + 150y 取最大值Ζ
= 1, 2, 3, 4, 如图 4, 打出网格, 这时网格在可行域
内的交点, 即可行域内的整点Ζ
将直线 l1 向上平移到 l2 的位置时, 直线 l2 最
先经过可行域内的整点B (5, 2) , 且使 z = 160x +
252y 取最小值, 此时
z 最小= 160×5+ 252×2= 1304.
2000 年 第 3 期 数学通报
19
如何寻找《线性规划问题》的整点最优解
安培录 (山西省代县中学校 034200)
试验教材高二数学 (上) 增加了《简单的线性
规划》的内容, 利用图解法解答线性规划的两类问 题Ζ 对此, 大纲要求“会简单的应用”Ζ
学生对线性规划的基本概念、基本方法在两
类实际问题中的应用, 基本可以达纲, 但对寻找 《线性规划问题》的整点最优解的问题, 感到不好 入手, 完成作业困难较大Ζ 在这个问题上, 试验教 材安排了一个例题 (P 76 页例 4) , 两个习题 (P 79 页第 3、4 题) , 一个复习题 (P 107 页第 17 题) Ζ 针 对学生从认知到应用这一过程存在的问题, 笔者 在教学实践中归纳整理了三种基本方法, 现举例 说明如下:
线性规划问题的四种求解方法

可画出直线
l0
:y
=-
2 3
x
,
把直线
l0
向右上方
平移 , 当经过可行域上点 B 时 , 直线的截距最
大 .此时 z = 12x +18y 取最大值 .解方程组
z =6x +3y +5[ 300 -(x +y)] +5(200 -x ) +9(450 -y)+6(100 +x +y)=2 x -5y +
解 设每天生产甲 、乙产品的件数分别是
维生素 B (单位 / 千克) 800 400 500
成本(单位 / 千克) 11 9 4
某食物营养所想用 x 千克甲种食物 , y 千 克乙种食物 , z 千克丙种食物配成 100 千克混合 物 , 并使混合物至少含有 56000 单位维生素 A 和 63000 单位维生素 B
问题的最优解具有十分重要的现实意义 .现介
二 、等值线法
绍几种求解线性规划问题的最优解的策略 .
所谓等值线是指直线上任一点的坐标(x ,
一 、截距法
y )都使 F(x , y)=Ax +By 取等值C 的直线l :
例 1 某厂需从国外引进两种机器 .第一 Ax +By = C(A 、B 不同时为零).通过比较等
7150 作出以上不等式组所表示的平面区域即可
x +2y 4x +y
=13得 =24
B(5 , 4).故当
x
=5, y
=4
行域 .令 z = 0 , 则可画出 直线 l 0 :2x -5y + 7150 =0 .画出一组与 l 0 平行的等值线 , 比较等
线性目标函数最优解的求解方法
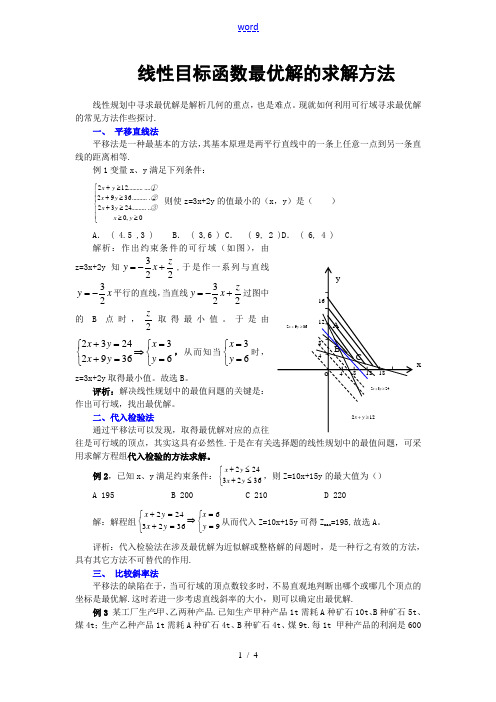
线性目标函数最优解的求解方法线性规划中寻求最优解是解析几何的重点,也是难点。
现就如何利用可行域寻求最优解的常见方法作些探讨.一、 平移直线法平移法是一种最基本的方法,其基本原理是两平行直线中的一条上任意一点到另一条直线的距离相等.例1变量x 、y 满足下列条件:⎪⎪⎩⎪⎪⎨⎧≥≥≥+≥+≥+0,0............2432...........3692..............122y x ③y x ②y x ①y x 则使z=3x+2y 的值最小的(x ,y )是( )A . ( 4.5 ,3 )B . ( 3,6 )C . ( 9, 2 )D . ( 6, 4 ) 解析:作出约束条件的可行域(如图),由z=3x+2y 知223zx y +-=,于是作一系列与直线x y 23-=平行的直线,当直线223zx y +-=过图中的B 点时,2z取得最小值。
于是由⎩⎨⎧==⇒⎩⎨⎧=+=+6336922432y x y x y x ,从而知当⎩⎨⎧==63y x 时,z=3x+2y 取得最小值。
故选B 。
评析:解决线性规划中的最值问题的关键是:作出可行域,找出最优解。
二、代入检验法通过平移法可以发现,取得最优解对应的点往往是可行域的顶点,其实这具有必然性.于是在有关选择题的线性规划中的最值问题,可采用求解方程组代入检验的方法求解。
例2,已知x 、y 满足约束条件:⎩⎨⎧≤+≤+3623242y x y x ,则Z=10x+15y 的最大值为()A 195B 200C 210D 220解:解程组⎩⎨⎧==⇒⎩⎨⎧=+=+963623242y x y x y x 从而代入Z=10x+15y 可得Z max =195,故选A 。
评析:代入检验法在涉及最优解为近似解或整格解的问题时,是一种行之有效的方法,具有其它方法不可替代的作用.三、 比较斜率法 平移法的缺陷在于,当可行域的顶点数较多时,不易直观地判断出哪个或哪几个顶点的坐标是最优解.这时若进一步考虑直线斜率的大小,则可以确定出最优解.例3 某工厂生产甲、乙两种产品.已知生产甲种产品1t 需耗A 种矿石10t 、B 种矿石5t 、煤4t ;生产乙种产品1t 需耗A 种矿石4t 、B 种矿石4t 、煤9t.每1t 甲种产品的利润是600元,每1t 乙种产品的利润是1000元.工厂在生产这两种产品的计划中要求消耗A 种矿石不超过300t 、B 种矿石不超过200t 、煤不超过360t .甲、乙两种产品应各生产多少(精确到0.1t ),能使利润总额达到最大?解:设生产甲、乙两种产品分别为xt 、yt ,利润总额为z 元,那么⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+≤+0,0360942004515025y x y x y x y x 且Z=600x+1000y 作出约束条件所表示的平面区域(如左图),即可行域. 作直线l :600x+1000y=0,即直线l :3x+5y=0.因为94534525-<-<-<-,即k EN <k MN <k l <k FN ,所以把直线l 向上方移至m 的位置,直线经过可行域上的点M ,此时Z=600x+1000y 取最大值.解方程组⎩⎨⎧=+=+3609420045x x y x 得M 的坐标x=29360=12.3,y=291000=34.5,代入计算得Z max =291216000. 答:应生产甲产品约12.3t,乙产品34.5t ,能使利润总额达到最大.评析:这是高中新教材第二册上册第七章,“简单的线性规划”一节中的例3(P62~63),确定了直线斜率的大小,实质是确定了直线在向上平移的过程中,在经过可行域X 围内时,即可确定最优解。
