统计学例题
统计学计算题例题(含答案)
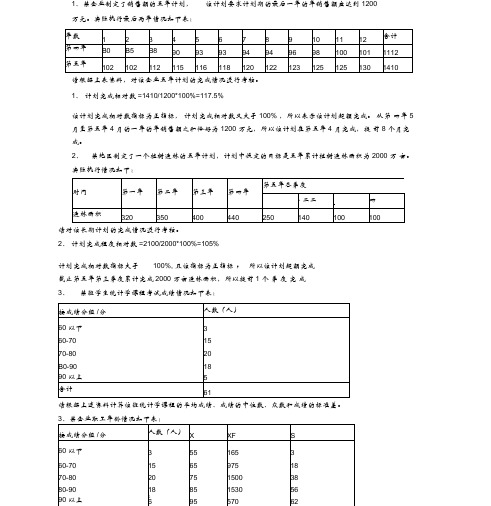
1、某企业制定了销售额的五年计划, 该计划要求计划期的最后一年的年销售额应达到 1200万元。
实际执行最后两年情况如下表:请根据上表资料,对该企业五年计划的完成情况进行考核。
1、 计划完成相对数 =1410/1200*100%=117.5%该计划完成相对数指标为正指标, 计划完成相对数又大于 100% ,所以表示该计划超额完成。
从第 四年 5 月至第五年 4 月的一年的年销售额之和恰好为 1200 万元,所以该计划在第五年 4 月完成,提 前 8 个月完成。
2、 某地区制定了一个植树造林的五年计划,计划中设定的目标是五年累计植树造林面积为 2000 万 亩。
实际执行情况如下:请对该长期计划的完成情况进行考核。
2、 计划完成程度相对数 =2100/2000*100%=105%计划完成相对数指标大于100%, 且该指标为正指标 , 所以该计划超额完成截止第五年第三季度累计完成 2000 万亩造林面积,所以提前 1 个 季 度 完 成3、某班学生统计学课程考试成绩情况如下表:请根据上述资料计算该班统计学课程的平均成绩、成绩的中位数、众数和成绩的标准差。
3、某企业职工年龄情况如下表:X 二三于=4740/62=76.45 (分)Me=70+ (62/2-18) *10/20=76.5 (分)Mo=70+(20 J5)70/[(2CM5)+(2CM8)]=77 」4 (分)G-7(55-76.45f *3 +⋯⋯+ (95^76.45f *6/62=10.45 (分)4、某学校有5000 名学生,现从中按重复抽样方法抽取250 名同学,调查其每周观看电视的小时数的情况,获得资料如下表:请根据上述资料,以95% 的概率保证程度对全校学生每周平均收看电视时间进行区间估计。
4> 样本平均数X= Sxf/Sf-l250/250-5样 ______________ __________二>/ 刀(好予f/(工f—1 )二V 1136/249 二2. 14抽样平均误差U 二s/ Vn=0.14因为 F (t) =95%, 所以日.96抽样极限误差△ 二t U 二 1. 96*0. 14=0. 27 区间下限=5-0. 27=4. 73 区间上限二5+0. 27-5. 27全校学生每周平均收看电视的吋间在( 4.73,5.27) 小时之间,概率保证程度为95%5 、某企业对全自动生产线上的产品随机抽取1000 件进行检验,发现有45 件是不合格的,设定允许的极限误差为1.32% 。
统计学例题

、7.7 某大学为理解学生每天上网旳时间,在全校7 500名学生中采用反复抽样措施随机抽取36人,调查他们每天上网旳时间,得到下面旳数据(单位:小时):求该校大学生平均上网时间旳置信区间,置信水平分别为90%,95%和99%。
解:(1)样本均值x=3.32,样本原则差s=1.61;(2)抽样平均误差:反复抽样:σ≈.61/6=0.268不反复抽样:σ=x≈8=0.267(3)置信水平下旳概率度:1α-=0.9,t=2zα=0.05z=1.6451α-=0.95,t=2zα=0.025z=1.961α-=0.99,t=2zα=0.005z=2.576(4)边际误差(极限误差): x x x t z ασσ∆=⋅=⋅1α-=0.9,2x x x t z ασσ∆=⋅=⋅=0.05x z σ⋅反复抽样:2x x z ασ∆=⋅=0.05x z σ⋅=1.645×0.268=0.441 不反复抽样:2x x z ασ∆=⋅=0.05x z σ⋅=1.645×0.267=0.4391α-=0.95,2x x x t z ασσ∆=⋅=⋅=0.025x z σ⋅反复抽样:2x x z ασ∆=⋅=0.025x z σ⋅=1.96×0.268=0.525 不反复抽样:2x x z ασ∆=⋅=0.025x z σ⋅=1.96×0.267=0.5231α-=0.99,x x x t z ασσ∆=⋅=⋅=0.005x z σ⋅反复抽样:2x x z ασ∆=⋅=0.005x z σ⋅=2.576×0.268=0.69不反复抽样:x x z ασ∆=⋅=0.005x z σ⋅=2.576×0.267=0.688(5)置信区间:(),x x x x -∆+∆1α-=0.9,反复抽样:(),x x x x -∆+∆=()3.320.441,3.320.441-+=(2.88,3.76)不反复抽样:(),x x x x -∆+∆=()3.320.439,3.320.439-+=(2.88,3.76)1α-=0.95,反复抽样:(),x x x x -∆+∆=()3.320.525,3.320.525-+=(2.79,3.85)不反复抽样:(),x x x x -∆+∆=()3.320.441,3.320.441-+=(2.80,3.84)1α-=0.99,反复抽样:(),x x x x -∆+∆=()3.320.69,3.320.69-+=(2.63,4.01)不反复抽样:(),x x x x -∆+∆=()3.320.688,3.320.688-+=(2.63,4.01)7.9 某居民社区为研究职工上班从家里到单位旳距离,抽取了由16个人构成旳一种随机样本,他们到单位旳距离(单位:km)分别是:10 3 14 8 6 9 12 11 7 5 10 15 9 16 13 2假定总体服从正态分布,求职工上班从家里到单位平均距离旳95%旳置信区间。
统计学经典例题(暨南大学出版社)

例1:某公司下属各店职工按工龄分组情况(1)(年)(2)例2:水果甲级每元1公斤,乙级每元1.5公斤,丙级每元2公斤。
问:(1)若各买1公斤,平均每元可买多少公斤? (2)各买6.5公斤,平均每元可买多少公斤?(3)甲级3公斤,乙级2公斤,丙级1公斤,平均每元可买几公斤? (4)甲乙丙三级各买1元,每元可买几公斤? (1)(2)(3) (4)例3:自行车赛时速:甲30公里,乙28公里,丙20公里,全程200公里,问三人平均时速是多少?若甲乙丙三人各骑车2小时,平均时速是多少?例4:某牛群不同世代的规模分别为:0世代200头,1世代220头,2世代210头,3世代190头,4世代210头。
试求其平均规模。
例5:假定某地储蓄年利率(按复利计算):5%持续1.5年,3%持续2.5年,2.2%持续1年。
请问此5年内该地平均储蓄年利率。
75.64155.75.31=+++==∑nx一店平均工龄)(425.3205.681361011535.765.3101年五店平均工龄==+++⨯+⨯+⨯+⨯==∑∑fxf )/(38.11667.23215.111131元公斤==++==∑nnH )/(38.10833.145.195.6215.65.115.6115.65.65.61元公斤==⨯+⨯+⨯++==∑∑fxf H )/(24.183.4612125.113111231元公斤==⨯+⨯+⨯++==∑∑fxf H 元)(公斤/5.1325.11=++==∑nxx )/(2.2581.236002002012002812003012002002001小时公里==⨯+⨯+⨯++==∑∑fx f H )/(266156222220228230fxf x 小时公里==++⨯+⨯+⨯==∑∑11111152002202101902101205()()H ==++++头1.5 2.5(1)100%1)100% 3.43%G +=-⨯=-⨯=该地平均储蓄年利率例1:从10000盒火柴中,随机抽取50盒,算得样本平均数为49根,样本均方差为2根.求其抽样平均误差。
统计学例题

一、判断题1.社会经济统计的研究对象是社会经济现象总体的各个方面。
( x)2.统计调查过程中采用的大量观察法,是指必须对研究对象的所有单位进行调查。
( x)3.总体的同质性是指总体中的各个单位在所有标志上都相同。
(x)4.某一职工的文化程度在标志的分类上属于品质标志,职工的平均工资在指标的分类上属于质量指标。
(v)5.总体单位是标志的承担者,标志是依附于总体单位的。
(v)6.全面调查和非全面调查是根据调查结果所得到的资料是否全面来划分的。
(x)7.对我国主要粮食作物产区进行调查,以掌握全国主要粮食作物生长的基本情况,这种调查是重点调查。
(v)8.在对现象进行分析的基础上,有意识地选择若干具有代表性的单位进行调查,这种调查属于重点调查。
(x)9.统计分组的关键问题是确定组距和组数。
(x)10.分配数列的实质是把总体单位总量按照总体所分的组进行分配。
(v)11.某企业职工按文化程度分组形成的分配数列是一个单项式分配数列。
(x)12.连续型变量和离散型变量在进行组距式分组时,均可采用相邻组组限重叠的方法确定组限。
(v)13.分组以后,各组的频数越大,则组的标志值对于全体标志水平所起的作用也越大;而各组的频率越大,则组的标志值对全体标志水平所起的作用越小。
(x)14.同一个总体,时期指标值的大小与时期长短成正比,时点指标值的大小与时点间隔成反比。
(v)15.某企业生产某种产品的单位成本,计划在上年的基础上降低2%,实际降低了3%,则该企业差一个百分点,没有完成计划任务。
(x)16.某年甲、乙两地社会商品零售额之比为1:3,这是一个比例相对指标。
(x)17.全国粮食总产量与全国人口数对比计算的人均粮食产量是平均指标。
(x)18.根据分组资料计算算术平均数,当各组单位数出现的次数均相等时,按加权算术平均数计算的结果与按简单算术平均数计算的结果相同。
(v)19.权数对算术平均数的影响作用只表现为各组出现次数的多少,与各组次数占总次数的比重无关。
统计学例题

返回ห้องสมุดไป่ตู้
【例1】某流水生产线有前后衔接的五道工序。某日各工序产品的合格率分别 为95﹪、92﹪、90﹪、85﹪、80﹪,求整个流水生产线产品的平均合格率。 分析:设最初投产100A个单位 ,则 第一道工序的合格品为:100A×0.95; 第二道工序的合格品为:100A×0.95)×0.92; …… 第五道工序的合格品为:100A×0.95×0.92×0.90×0.85)×0.80; 因该流水线的最终合格品即为第五道工序的合格品, 故该流水线 总的合格品应为: 100A×0.95×0.92×0.90×0.85×0.80; 则该流水线产品总的合格率为:
L
中位 数组
500以下 U 500~800 800~1100 1100~1400 1400~1700 1700~2000 2000以上 合计
Sm-1
40 130 240 345 415 465 500 ——
500 460 370 260 155 85 35
Sm+1
上限公式: 下限公式:
返回
U
众数组
返回
【例】 12个商学院的毕业生每月起薪的数据如下: 2210 2255 2350 2380 2380 2390 2420 2440 2450 2550 2630 2825
M1
M2
M3
M1=(2350+2380)/2=2365(美元) M3=(2450+2550)/2=2500(美元)
R=2825 –2210=615(美元)
【例】某企业某日工人的日产量资料如下:
日产量(件)x 10 11 12 13 14 合计
各组工人日总产量(件)m 700 1100 4560 1950 1400 9710
统计学计算题例题
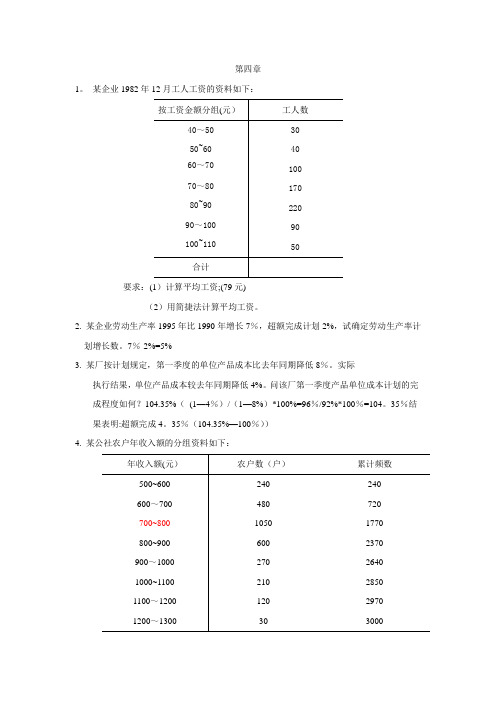
第四章1。
某企业1982年12月工人工资的资料如下:要求:(1)计算平均工资;(79元)(2)用简捷法计算平均工资。
2. 某企业劳动生产率1995年比1990年增长7%,超额完成计划2%,试确定劳动生产率计划增长数。
7%-2%=5%3. 某厂按计划规定,第一季度的单位产品成本比去年同期降低8%。
实际执行结果,单位产品成本较去年同期降低4%。
问该厂第一季度产品单位成本计划的完成程度如何?104.35%((1—4%)/(1—8%)*100%=96%/92%*100%=104。
35%结果表明:超额完成4。
35%(104.35%—100%))4. 某公社农户年收入额的分组资料如下:要求:试确定其中位数及众数。
中位数为774.3(元)众数为755。
9(元)求中位数:先求比例:(1500—720)/(1770—720)=0.74286分割中位数组的组距:(800—700)*0。
74286=74.286加下限700+74。
286=774。
286求众数:D1=1050-480=570D2=1050—600=450求比例:d1/(d1+d2)=570/(570+450)=0.55882分割众数组的组距:0。
55882*(800—700)=55.882加下限:700+55.882=755.8825.1996年某月份某企业按工人劳动生产率高底分组的生产班组数和产量资料如下:.64。
43(件/*140+85*60)/)6。
根据表中资料计算中位数和众数.中位数为733。
33(元)众数为711.11(元)求中位数:先求比例:(50—20)/(65—20)=0。
6667分割中位数组的组距:(800-600)*0.6667=66。
67 加下限:600+66.67=666。
677.某企业产值计划完成103%,比去年增长5%。
试问计划规定比去年增长 多少?1.94%(上年实际完成1。
03/1.05=0.981 本年实际计划比上年增长(1—0。
统计学重要例题
)(1235)1014()814(8141200个=⨯-+--+= M解:顺序数据本身就是排序的,根据中位数位置的确定公式:300+1÷2=150.5从累积频数看,中位数在―一般‖这一类中,即Me = 一般【例4.5】根据第三章表3-5中的数据,计算50 名工人日加工零件数的中位数 )(21.12351416250120个=⨯-+= e M 107 108 108 110 112 112 113 114 115 117 117 117 118 118 118 119 120 120 121 122 122 122 122 123 123 123 123 124 124 124 125 125 126 126 127 127 127 128 128 129 130 131 133 133 134 134 135 137 139 139 【例4.6】根据9个家庭的收入调查数据,要求计算人均月收入的四分位数。
1500 750 780 1080 850 960 2000 1250 1630 解:750 780 850 960 1080 1250 1500 1630 2000 根据公式QL 位置 =n /4=9/4=2.25QL= 780 + (850-780)*0.25 = 797.5(元)QU 位置 =3n/4=3×9/4=6.75 QU=1250 + (1500-1250) ×0.75 = 1437.5(元)【例4.7】计算50 名工人日加工零件数的四分位数QL 位置=50/4=12.5)(81.117588450115个=⨯-+= L QQU 位置=3×50/4=37.5)(75.128510304503125个=⨯-⨯+= U Q 【例4.8】计算第三章中50个工人日加工零件数的均值 X= (117+122+……121)/50 = 6149/50 = 122.98(个)【例4.10】一位投资者持有一种股票,2001-2004年的收益率分别为4.5%,2.1%,25.5%,1.9%要求计算该投资者在这4年内的平均收益率。
统计学第五章例题
第五章例题【例5-1】已知某地区2010年底常住人口为8559人,其中,暂时住外地人口为2342人,外地暂住本地区人口为5576人,求2010年底现有人口数。
【例5-2】某企业2011年制定的产值目标为2000万元,该企业历年劳动生产率最高1000元/人,要求推算该企业工人人数至少应为多少,才能完成该目标规定任务。
【例5-3】根据过去的数据得知某地区农民人居纯收入来源中工资性收入占44.11%,家庭经营纯收入占48.68%,财产性收入占1.26%,转移性收入占5.94%。
如果该地区农民人均纯收入为5000元,要求按来源分别计算各种收入。
【例5-4】某地区1966-1971年工业总产值由于某种原因缺失了,仅有1965年年报资料为1299万元,,1972年年报资料为1670万元,要求补全中间6年的历史资料。
【例5-5】某企业所属5个食品加工厂,某年某种产品的生产量及生产费用资料如表5-1所示。
该企业另一个年产240吨的食品加工厂,由于费用资料不全,不能及时汇总。
【例5-6】某市有3个百货商店,表5-2中1,2,3,4栏为已知数据资料,要求据此计算分析该市3个百货商店第一季度零售计划完成情况以及上半年零售额计划累计完成情况表5-2百货商店的数据资料【例5-7】某市计划去年人口自然增长率12‰,实际增长率为11.5‰,要求计算该市去年人口自然增长率计划完成程度。
【例5-8】某企业计划规定劳动生产率比上年提高10%,实际提高15%,要求计算该企业劳动生产率计划完成程度。
【例5-9】某产品按5年计划规定,最后一年产量应达到50万吨,计划执行情况如表5-3所示。
表5-3某产品的执行情况要求检查其计划执行情况。
【例5-10】某地区“十一五”时期计划规定其基本建设投资总额为20亿元,实际执行21亿元,截止到2010年5月15日实际完成投资总额累计已达到20亿元,要求用累计法检查其计划完成情况。
【例5-11】某城市有人口200万人,有零售商店4000个,要求计算该城市零售网点密度。
统计学例题-统计整理
-
-
29
例:单项式分组
育龄妇女生育子女存活数
按存活数分组(个)
0 1 2 3 4 5 合计
人数 f
7 24 35 20 10 4 100
2019/10/31
30
例:品质数列
按企业类型分组
国有企业 独资企业 合资企业 民营企业
合计
频数 f
24 35 20 10
89
2019/10/31
品质数列
31
例:组限的重叠(连续)排列
—
次数/频数
第三章 统计数据的整理
34
志值 D.总体各单位具有某一共同的品质标志或数量标志。
简单现象总体
车间名称
一车间 二车间 合计
产量(万件)
2011 f0 9 6
2012 f1 14 12
15
26
4
复杂现象总体
产品
A 产品 B 产品 C 产品 合计
产量
单位
f
吨
900
千件
160
立方米
500
-
-
5
简单现象总体(与前比较)
产 品 单位
认识统计总体:
3,调查某市的失业率,则调查对象是全市的:
A.就业人口, B.失业人口, C.总人口, D.经济活动人口(A+B)。
统计总体的同质性指:
A.总体各单位具有全部共同的品质标志或数量标志 B.总体各单位具有全部共同的品质标志属性或数量标
志值 C.总体各单位具有某一共同的品质标志属性或数量标
第三章 统计数据的整理
20
例 某企业电子元件耐用时数抽样资料
单位:小时
830 880 1 170 1 080 1 250 1 360 1 410 1170
统计学计算题例题(含答案)
1、某企业制定了销售额的五年计划,该计划要求计划期的最后一年的年销售额应达到1200万元。
实际执行最后两年情况如下表:请根据上表资料,对该企业五年计划的完成情况进行考核。
1、计划完成相对数=1410/1200*100%=117.5%该计划完成相对数指标为正指标,计划完成相对数又大于100%,所以表示该计划超额完成。
从第四年5月至第五年4月的一年的年销售额之和恰好为1200万元,所以该计划在第五年4月完成,提前8个月完成。
2、某地区制定了一个植树造林的五年计划,计划中设定的目标是五年累计植树造林面积为2000万亩。
实际执行情况如下:请对该长期计划的完成情况进行考核。
2、计划完成程度相对数=2100/2000*100%=105%计划完成相对数指标大于100%,且该指标为正指标,所以该计划超额完成截止第五年第三季度累计完成2000万亩造林面积,所以提前1个季度完成3、某班学生统计学课程考试成绩情况如下表:请根据上述资料计算该班统计学课程的平均成绩、成绩的中位数、众数和成绩的标准差。
4、某学校有5000名学生,现从中按重复抽样方法抽取250名同学,调查其每周观看电视的小时数的情4> 样本平均数X= Sxf/Sf-l250/250-5样 ________ __________二>/刀(好予f/(工f—1)二V 1136/249二2. 14抽样平均误差U二s/ Vn=0.14因为F (t) =95%,所以日.96抽样极限误差△二t U 二 1. 96*0. 14=0. 27 区间下限=5-0. 27=4. 73 区间上限二5+0. 27-5. 27全校学生每周平均收看电视的吋间在(4.73,5.27)小时之间,概率保证程度为95%5、某企业对全自动生产线上的产品随机抽取1000件进行检验,发现有45件是不合格的,设定允许的极限误差为 1.32%。
请对全部产品的合格率进行区间估计。
5、样本合格率p=955/1000=95.5% 抽样平均误差u二V pChp)/n= 0.66%因为△=1.32%,所以t= A/ u =2所以F.(.t)-95. 45%区间下限二95. 5%-l. 32%=94. 18%区间上限二95. 5%+l. 32%二96. 82%所以我们以95. 45%的概率估计全部产品和合格率是在(94.18%, 96. 82%)之间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P99某市2002~2010年居民消费品购买力和居民货币收人统计数据如下:(单位:十亿
根据上述统计数据,试:
(1)建立一元线性回归模型;
(2)对回归模型进行显著性检验(取α=0.05;已知R0.05(7)=0.666,
R0.05(9)=0.602)
(3)若11年居民货币收入增长19%,预测该市2011年居民消费品购买力;
注:计算结果保留至小数点后4位。
解:设居民消费品购买力为y,居民货币收入为x则:
(1)设一元线性回归模型为:
列表计算相关数据如下:
则回归系数
故所求一元线性回归模型为 :
(2)由
在显著性水平 自由度=n-m=9-2=7时,由已知得
由于R>R0.05(7) 知检验通过,即 X 与Y 间线性关系显著。
(3)由题意知:2011年居民货币收入为 (十亿元)代入模型知2011年居民消费品购买力为:
(十亿元)
()22295875.70232.0187.6ˆ0.847297207.76232.0n xy x y b n x x -⨯-⨯==≈⨯--∑∑∑∑∑11232.0ˆˆ187.60.84720.994599x a y b n n =-=⨯-⨯=-∑
∑ˆ0.99450.8472y x =-+0.9997
n xy x y R -=
==0.05α=()0.05
70.666
R =47.8 1.1956.882⨯=2011ˆ0.99450.847256.88247.1959y =-+⨯=
例例1某市2002~2010年化纤零售量如下表所示:(单位万元)
试选择合适的预测模型,用最小平方法估计参数。
预测2011年的销售额及置信度为95%的
预测区间。
已知t 0.025(9)=2.26,t 0.025(7)=2.365。
注:计算结果保留至小数点后4位。
解:1)设销售额为 由已知条件知序列的一阶差分大体接近,故可配合直线预测模型:
列表计算相关数据如下: 则回归系数
故所求直线预测模型为:
以 代入预测模型,可得2011年的销售额预测值为
(万元) t y bt a y
t +=ˆ3636ˆ4049t y a n ===∑2209234.866760t ty b t ===∑∑ˆ40434.8667t y t =+05t =2011ˆ40434.86675578.3335
y =+⨯=
又:
当显著性水平 时,自由度为 时,由已知得
故所求 预测区间为:
=
=
即有95%的把握预测:
2011年该商店的销售额在 万元至 万元之间。
2.1691y s ===α0.05=927n m -=
-=()()0.025
227 2.365t n t α-==()
20112ˆ2y
y t n s α-⋅⋅
578.3335 2.365 2.1691⨯⨯578.3335 6.3408571.9927584.6743
已知市场上有A 、B 、C 三种牌子的电视机。
当月的市场占有率分别为30%,40%,30%且已知转移概率矩阵为
P= 求两个月后三个牌子的电视机的市场占有率及终极市场占有率。
注:计算结果保留至小数点后2位。
解:由题意知:
由 知
即两个月后,A 、B 、C 三种牌子电视机的市场占有率分别为68%,16%及16%。
设其终极市场占有率为
由 0.80.10.10.60.20.20.40.30.3⎛⎫ ⎪ ⎪ ⎪⎝⎭
()0
0.30.40.3s =0.80.10.10.60.20.20.40.30.3P ⎛⎫ ⎪= ⎪ ⎪⎝⎭0k k s s P =()22020.80.10.10.30.40.30.60.20.20.40.30.3s s P ⎛⎫ ⎪== ⎪ ⎪⎝⎭()()0.80.10.10.600.200.200.60.20.20.680.160.160.40.30.3⎛⎫ ⎪== ⎪ ⎪⎝⎭
()
123x x x α=1231P x x x αα=⎧⎨++=⎩()()()()
123112321233
1230.80.60.410.10.20.320.10.20.3314x x x x x x x x x x x x x x x ++=⎧⎪++=⎪⇒⎨++=⎪⎪++=⎩
由(2)-(3)知: 代(5)入(4)知: 代(5)(6)入(1)得:
即:
由(5)(6)知:
即A 、B 、C 三种牌子电视机的终极市场占有率分别为72%,14%及14%。
案例2 某工程队承担一座桥梁的施工任务。
由于施工地区夏季多雨,需停工三个月。
在停工期间该工程队可将施工机械搬走或留在原处。
如搬走,需搬运费1800元。
如留原处,一种方案是花500元筑一护堤,防止河水上涨发生高水位的侵袭。
若不筑护堤,发生高水位侵袭时将损失10000元。
如下暴雨发生洪水时,则不管是否筑护堤,施工机械留在原处都将受到60000元的损失。
据历史资料,该地区夏季高水位的发生率是25%,洪水的发生率是2%,试用决策树法分析该施工队要不要把施工机械搬走及要不要筑堤?
23
x x =()5()12
126x x =-()222
20.8120.60.412x x x x -++=-221.40.20.14
x x =⇒=1230.72,0.14
x x x ===
-1800-18000-600000
0搬走
不搬筑护堤
不筑
堤高水位0.25
高水位0.25
洪水0.02
洪水0.02其它水位0.73其它水位0.73
-1700-3700-500-1700-1700
例:某电器公司考虑是否把一种新电器投放市场.公司决策者估计,这种新电器畅销的概率为o.6,滞销的概率为0.4。
如果畅销,则可获利40000
元。
如果滞销,则亏损35000元.在决策前,公司花费10000元聘请市场调查机构对该电器的销路作一调查。
调查结果与实际情况之间的关系如下: 那么,该公司若根据经验的知识(即先验概率),不进行市场调查,应如何决定?若进行市场调查,又应如何作决策? 是否有必要作市场调查?
解:设投放市场与不投放市场分别用 与 表示,畅
销与滞销分别用 和 表示;调查结果为畅销与滞销分别用H 1和H 2表示由题意知损益表为:
1α2α
1θ2θ。
