证明三角形内角和的几种方法
“三角形内角和是180°”的验证教学

“三角形内角和是180°”的验证教学几种常见方法的比较验证“三角形的内角和是180°”,常见的有三种方法:(1)用量角器量出三个角的度数,然后加起来看是不是180°(简称“测量求和法”);(2)将三角形三个角剪下来,再将它们拼在一起看能不能组成平角(简称“剪拼法”);(3)将三个角折起来拼在一起,看能不能组成平角(简称“折拼法”)。
这三种方法中,“测量求和法”的优点是:接近学生的思维水平,课堂上学生很容易想到,也很容易理解;缺点是:“测量”存在着误差,因此测得的三个角的度数加起来往往都不是180°。
这使得测量结果非但不能验证结论,相反却易给人造成“三角形内角和不是180°”的错误印象。
“剪拼法”的优点是:操作简单、看起来一目了然;缺点是:破坏了原图形,不能很好地体现原图形与撕下来后图形间的联系与变化。
“折拼法”有效地避免了量、撕的缺陷,可惜操作起来方法不明──学生并不能十分清楚地掌握折的方法。
因此,我们对教材中的“折拼法”方案稍作改进:首先让学生折“高”找到对应的“垂足”,然后将三角形三个“顶点”分别对准“垂足”进行折叠就行了(如图1)。
经改进操作起来简捷多了。
其实,对于三角形内角和的三种常见验证方法,或多或少都存在着误差。
用任何一种方法验证“三角形内角和是180°”,都不足以让人信服。
因此,让尽量多的验证方法出现在课堂上,“让各种方法相互解释、互相佐证”是上好这节课的关键。
然而事实并不随你我所愿。
正常情况下,学生上课时只能想到“量”这一种方法,其他方法的出现,充其量仅仅是一两个“优等生闻道预先”。
如何通过教师艺术的启发,引导出多样的验证方法呢?我们对课堂中可能出现的种种情况进行了预设:学生猜想“三角形内角和是180°”,教师将猜想板书在黑板上追问:三角形内角和真的是180°吗?说说你的依据。
(1)“测量求和法”的引出:采用“一点突破”,紧扣“内角和”逐步逼近。
初中几何证明口诀

初中几何证明口诀在初中几何中,证明是学习的重要内容之一、通过证明,可以巩固和提高自己对几何知识的理解和应用能力。
以下是一些常用的初中几何证明口诀:1.三角形的内角和定理:三角形内角和为180度。
可以通过绘制平行线、共线线段等方法证明。
2.外角定理:三角形的外角等于其余两个内角的和。
可以通过绘制平行线等方法证明。
3.垂直角定理:垂直角相等。
可以通过绘制平行线、共线线段等方法证明。
4.同位角定理:同位角相等。
可以通过平行线等方法证明。
5.三角形的相似性定理:相似三角形的对应角相等,对应边成比例。
可以通过AA、SSS、SAS等方法证明。
6.圆周角定理:圆周角是圆心角的两倍。
可以通过绘制弧、使用同位角等方法证明。
7.弦切角定理:弦切角等于其对应的弧的一半。
可以通过绘制切线、弧等方法证明。
8.正方形的特性:正方形的四条边相等,四个角为直角。
可以通过对角线等方法证明。
9.等腰三角形的特性:等腰三角形的两边相等,两个底角相等。
可以通过绘制高线等方法证明。
10.平行四边形的特性:平行四边形的对边相互平行,对角线相互平分。
可以通过角平分线等方法证明。
11.三角形的中线定理:三角形的三个中线交于一点,且这点距离三个顶点的距离是各边长的一半。
可以通过线段等方法证明。
12.直角三角形的勾股定理:直角三角形的两个直角边的平方和等于斜边的平方。
可以通过平行四边形等方法证明。
13.外切圆定理:三角形的外接圆的圆心是三个顶点的垂直平分线的交点。
可以通过角平分线、圆心角等方法证明。
14.圆的切线定理:切线与半径垂直。
可以通过绘制切线、使用垂直角等方法证明。
15.纵横切割定理:两条平行线被一条截线切割,那么两个内角和为180度。
可以通过平行线等方法证明。
这些口诀可以帮助初中生记住一些重要的初中几何证明定理,并引导他们学习如何使用特定的几何性质进行证明。
同时,更重要的是理解定理的证明过程,培养逻辑思维能力和几何推理能力。
三角形的内角和的证明方法

三角形的内角和的证明方法三角形内角和的证明:一次几何学的探索之旅在几何学的世界里,三角形是一个基础且重要的元素,它的性质和定理构成了许多复杂几何问题的基础。
其中,三角形的内角和定理是初等几何中的一个基本事实,它揭示了三角形内部三个角度的总和始终等于180度。
这个看似简单的定理,其实蕴含了丰富的几何思想和证明技巧。
本文将深入探讨这个定理的证明方法,以揭示其背后的数学魅力。
首先,我们可以从欧几里得几何的角度出发进行证明。
欧几里得,古希腊的数学家,他的《几何原本》是几何学的基石。
在第五公设中,他提出“在平面上,过直线外一点,只能画一条直线与已知直线平行”。
基于此,我们可以这样证明:假设三角形ABC,过点A画一条与BC平行的直线DE,那么∠BAD和∠BAC互补(因为DE平行于BC),同理,∠CAD和∠CAB互补。
所以,∠BAD+∠BAC+∠CAD=180°。
而∠BAC是∠BAD和∠CAD的公共角,所以∠B+∠C=∠BAD+∠CAD=180°-∠A,同样可以得到∠A+∠B=180°-∠C,∠A+∠C=180°-∠B。
三者相加,得到2(∠A+∠B+∠C)=360°,从而得出∠A+∠B+∠C=180°。
另一种证明方式是利用相似三角形。
如果两个三角形是相似的,那么它们的对应角相等。
考虑一个直角三角形ABC,∠C为90°,根据相似三角形的性质,我们可以得到∠A+∠B=90°。
现在,如果我们把直角三角形旋转180°,使其与原来的三角形重合,那么原来的∠C就会变成新的∠A或∠B,因此,新的三角形的三个角之和也是180°。
由于这两个角度的总和等于180°,所以原来的∠A+∠B+∠C也必须等于180°。
此外,我们还可以借助平面直角坐标系来证明。
假设三角形ABC的顶点在坐标轴上,那么可以将每个角表示为两条射线的夹角。
三角形内角和的计算

三角形内角和的计算三角形是平面几何中最基本的图形之一,它由三条边和三个内角组成。
计算三角形内角和对于解决与三角形相关的问题至关重要。
本文将通过介绍三角形内角和的计算方法,以及推导这些计算公式的过程,帮助读者更好地理解三角形的性质。
一、三角形内角和的定义在开始计算三角形内角和之前,我们首先来了解三角形内角和的定义。
三角形的内角和指的是三个内角的和,它始终等于180度。
这一性质可以通过直观的图形展示得到验证。
而计算三角形内角和的公式可以通过几何推导得出。
二、三角形内角和的计算方法1. 等边三角形(Equilateral Triangle)等边三角形是指三条边长度相等的三角形。
由于三边相等,每个内角也必然相等。
因此,等边三角形的每个内角都等于60度。
将三个60度的内角相加,结果是180度。
2. 直角三角形(Right-angled Triangle)直角三角形是指其中一个内角是90度的三角形。
有两种常见的情况,分别是直角在第一象限和直角在第四象限。
对于直角在第一象限的情况,另外两个内角的和等于90度,这是由于直角大小固定,所以可以推导出。
而对于直角在第四象限的情况,另外两个内角的和也等于90度,这是由于直角的性质决定的。
因此,对于直角三角形来说,一个角是90度,另外两个内角的和等于90度。
3. 一般三角形(General Triangle)对于一般的三角形,每个内角都没有固定的取值。
为了计算三角形内角和,我们可以使用以下公式:内角和 = 180度这个公式适用于所有类型的三角形,无论是等边三角形、直角三角形还是一般三角形。
通过该公式,我们可以推导出其他特殊类型三角形的内角和计算公式。
三、三角形内角和计算公式的推导在本节中,我们将推导出等腰三角形和任意三角形的内角和计算公式。
1. 等腰三角形(Isosceles Triangle)等腰三角形是指两边长度相等的三角形。
通常,等腰三角形的底边为底角边。
我们假设等腰三角形的底边两个角为α,斜边两个角为β,那么根据三角形内角和的计算公式,有:2α + β = 180度 ----(1)由于等腰三角形的两个底角相等,即α = α,所以:2α + 2α = 180度化简得:4α = 180度得出等腰三角形底角α的计算公式:α = 180度 / 4 = 45度将α = 45度代入等腰三角形底边两个角的和的计算公式(1),有:2(45度) + β = 180度化简得:90度+ β = 180度得出等腰三角形斜边β的计算公式:β = 180度 - 90度 = 90度结论:对于等腰三角形来说,两个底角为45度,斜边角为90度。
三角形的内角和定理的证明

三角形的内角和定理的证明
三角形的内角和定理是指任意三角形的三个内角的和等于180度。
在
数学中,三角形是最基本的几何图形之一,研究三角形性质的重要一环就
是研究三角形的内角和。
证明三角形的内角和定理可以通过几何方法或代
数方法。
下面我将通过几何方法进行证明。
证明三角形的内角和定理:
D_____________E
____________
由平行线的性质,得∠ACD=∠CDE(对应角)、∠CBD=∠CDE(同位角)。
则∠ACD+∠CBD=∠ACD+∠CDE+∠CBD=∠CDE+∠CDE=2∠CDE。
而∠ACB和∠CDE是同位角,根据同位角相等的性质,得∠ACB=∠CDE。
因此,∠ACB+∠CDE=∠ACB+∠ACB=2∠ACB。
类似地,我们还可以得到∠ABC+∠CDE=2∠ACB。
再根据同位角相等的性质,得∠ABC+∠ACB=∠ACB+∠ACB=2∠ACB。
综上所述,∠ACB+∠ABC+∠ACB=2∠ACB+2∠ACB=4∠ACB。
(1)
另一方面,由三角形的补角性质可知,∠ACB和∠ABC是补角,即
∠ACB+∠ABC=180度。
(2)
将方程(2)代入方程(1)中,得4∠ACB=180度,即∠ACB=45度。
所以,三角形的内角和定理得证,即∠ACB+∠ABC+∠ACB=180度。
综上所述,任意三角形的三个角的和等于180度,即三角形的内角和定理成立。
【注意】:
实际上,这个证明是利用了平行线和同位角的性质,通过构造了平行线DE来推导三角形的内角和定理。
三角形内角和的两种证明方法

三角形内角和的两种证明方法
嘿,朋友们!今天咱来聊聊三角形内角和的两种证明方法,这可超级有趣哦!
第一种方法呢,就像是搭积木一样。
想象一下,你有一个三角形,把它的三个角剪下来(就像从积木堆里挑出三块特定的积木),然后试着把它们拼在一起,哇塞,你会惊奇地发现它们竟然能拼成一个平角!这不就说明了三角形内角和是 180 度嘛!你说神奇不神奇?
再来说说第二种方法,这就像走迷宫找出口一样。
我们过三角形的一个顶点作对边的平行线(这不就像在迷宫里找到一条关键的路),然后通过一些巧妙的角度转换和推理,最后就能得出三角形内角和是 180 度啦!是不是很有意思呢?
所以呀,通过这两种方法,我们就能确切地知道三角形内角和真的就是180 度哟!简单又明了,对吧!。
三角形内角和180°证明7种方法
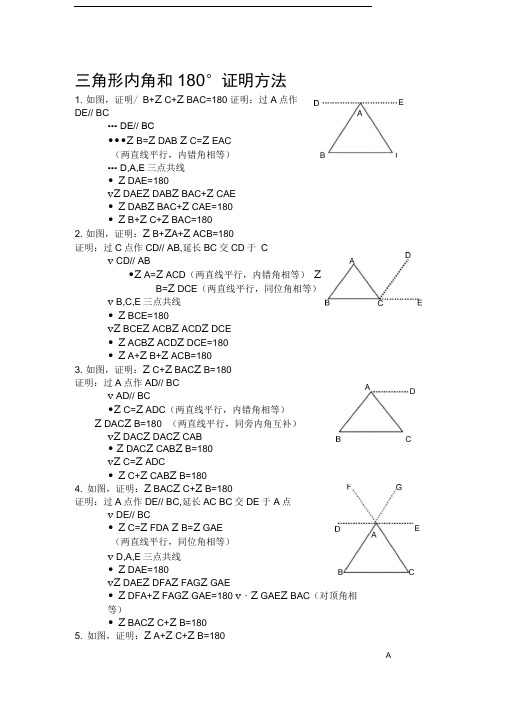
三角形内角和180°证明方法1. 如图,证明/ B+Z C+Z BAC=180 证明:过A点作DE// BC••• DE// BC•••Z B=Z DAB Z C=Z EAC(两直线平行,内错角相等)••• D,A,E三点共线•Z DAE=180vZ DAE Z DAB Z BAC+Z CAE•Z DAB Z BAC+Z CAE=180•Z B+Z C+Z BAC=1802. 如图,证明:Z B+Z A+Z ACB=180证明:过C点作CD// AB,延长BC交CD于 Cv CD// AB•Z A=Z ACD(两直线平行,内错角相等)ZB=Z DCE(两直线平行,同位角相等)v B,C,E三点共线•Z BCE=180vZ BCE Z ACB Z ACD Z DCE•Z ACB Z ACD Z DCE=180•Z A+Z B+Z ACB=1803. 如图,证明:Z C+Z BAC Z B=180°证明:过A点作AD// BCv AD// BC•Z C=Z ADC(两直线平行,内错角相等)Z DAC Z B=180°(两直线平行,同旁内角互补)vZ DAC Z DAC Z CAB• Z DAC Z CAB Z B=180°vZ C=Z ADC•Z C+Z CAB Z B=180°4. 如图,证明:Z BAC Z C+Z B=180°证明:过A点作DE// BC,延长AC BC交DE于A点v DE// BC•Z C=Z FDA Z B=Z GAE(两直线平行,同位角相等)v D,A,E三点共线•Z DAE=180vZ DAE Z DFA Z FAG Z GAE•Z DFA+Z FAG Z GAE=180 v・Z GAE Z BAC(对顶角相等)•Z BAC Z C+Z B=180°5. 如图,证明:Z A+Z C+Z B=180°EEA证明:作直线DE// AC FE// AB交BC于 EA•••DE// AC•••/ AFE+Z DEF=180 (两直线平行,同旁内角互补)/ C=Z DEB(两直线平行,同位角相等)•FE// AB•••/ AFE+/ A=180°(两直线平行,同旁内角互补)Z B=Z FEC(两直线平行,同位角相等)•••/ A=Z DEF•B,C,E三点共线•••Z BCE=180•Z BCE Z DEB Z DEF Z FEC•Z DEB Z DEF Z FEC =180°•Z A+Z C+Z B=180°6. 如图,证明:Z A+Z B+Z C=180 证明:作DE// AC, FG// AB MN/ BC,都交于点O•DE// AC•Z AFO Z FOD=180 (两直线平行,同旁内角互补)•FG// AB•Z AFO Z A=180°(两直线平行,同旁内角互补)•Z A=Z FOD•MN/ BC•Z C=Z FNO(两直线平行,同位角相等)•DE// AC•Z FNO Z DO(两直线平行,同位角相等)•Z C=Z DOM•MN/ BC•Z B=Z DM(两直线平行,同位角相等)•FG// AB•Z DMO Z FON(两直线平行,同位角相等)•Z B=Z FNO•M,O,N三点共线•Z MON=180•Z MON Z DOM Z DOF Z FON•Z DOF Z DOM Z FON=180•Z A+Z B+Z C=1807. 如图,证明:Z BAC Z CBA Z ACB=180证明:作DE// AC, FG// AB MN/ BC,都交于点O延长AC交FG于点K,延长AB到点L,延长BC交FG于点P• MN// BC•Z ABC Z AHN Z ACB Z ANM(两直线平行,同位角相等)•AB // FG•Z AHN Z FON Z BAC Z AKO(两直线平行,同位角相等)•••/ ABC=/ FON••• DE// AC •••/ ANM N DOM(两直线平行,同位角相等)/ OKA N DOF(两直线平行,内错角相等)•••N ACB N DOM••• FG// AB•/ BAC N OKA(两直线平行,同位角相等)•N BAC N DOF••• M,O,N三点共线•N MON=18°vZ MON N DOM N DOF N FON•/ DOM N DOF N FON=180•N BAC N CBA N ACB=180A。
三角形内角和

方法一: 方法一: 度量法
60° ° 45° ° 90° ° 30° °
90° °
30°+60°+ 80°= 180° ° ° °
45° °
45°+45°+90°=180 ° ° ° ° 其它三角形可以用量角器来度量。 其它三角形可以用量角器来度量。
方法二 :拼合法
拼法一
拼法二
刚才拼角的过程中你能想出证明的方法吗? 从刚才拼角的过程中你能想出证明的方法吗?
F
B
C
证法2: 证法 :
已知: 已知:△ABC 求证: 求证:∠A+∠B+∠C=180° ∠ ∠ ° 延长BC到 , 延长 到D,过C作CE∥BA 作 ∥ ∴∠A=∠ ∴∠ ∠1 两直线平行,内错角相等) (两直线平行,内错角相等) A ∠B=∠2 ∠ 两直线平行,内错角相等) (两直线平行,内错角相等) 又∵∠1+∠2+∠ACB=180° ∵∠1+∠2+∠ACB=180° 1+∠2+∠ACB=180 平角的定义) (平角的定义) B ∴∠A+∠B+∠ACB=180° ∴∠A+∠B+∠ACB=180° 等量代换) (等量代换)
B A
C
三角形内角和定理
三角形三个内角的和等于180 三角形内角和定理 三角形三个内角的和等于1800. ∠A+∠B+∠C=1800. △ABC中,∠A+∠B+∠C= 中 ∠A+∠B+∠C=
的几种变形: 三角形内角和定理的几种变形 ∠A=1800 –(∠B+∠C). ∠A= (∠B+∠C). ∠B=1800 –(∠A+∠C). ∠B= (∠A+∠C). ∠C=1800 –(∠A+∠B). ∠C= (∠A+∠B). B ∠A+∠B=1800-∠C. ∠A+∠B= ∠C. ∠B+∠C=1800-∠A. ∠B+∠C= ∠A. ∠A+∠C=1800-∠B. ∠A+∠C= ∠B. 这里的结论,以后可以直接运用.
