《大学物理》热学习题课 (1)
大学物理演示(热学)1(赵)

M Mdw
W是Mi的概率
20.2 统计物理学基础 20.2.1 微观量与宏观量
热学的研究对象: 大量微观粒子组成的宏观体系
热力学系统 或简称系统
阿伏伽德罗常数 NA= 6.023 ×10 23 /mol
宏观量: 描述系统整体特征的物理量.
宏观状态参量
如: 气体的 V, P, T...
微观量: 系如统: 中粒描子述的单m个,粒p子,特v征, 的物理量.
1) 常温常压下,分子的数密度
n~1025 / m3
2) 分子的平均平动动能
t
3 kT 2
3 1.381023 300
2
6.211021J 3.8810 2 eV
3) 氧气的方均根速率
2 3RT
M
3 8.31 300 3210 3
483 m/s
• ………
20 统计物理学基础
20.1 统计规律与概率理论
物质的微观模型
1.宏观物体由大量微粒—分子(原子)组成的
N A 6.022 1023 mol-1
2.物质的分子在永不停息地做无序热运动
扩散
布朗运动
f
3.物质的分子存在相互作用力
斥力 合力
f
rs
rt
(s t)
r0
O
r
s 9~15 t 4~7
20.2.2 平衡态与非平衡态 平衡态: 在不受外界影响的条件下,一个系统的宏观性质
不随时间改变的状态。
动态平衡
平衡态的特点
真空膨胀
p,V ,T
p',V ',T
1)单一性; 2)稳定性; 3)自发过程的终点; 4)热动平衡.
(完整版)大学物理热学习题附答案

一、选择题1.一定量的理想气体贮于某一容器中,温度为T ,气体分子的质量为m 。
根据理想气体的分子模型和统计假设,分子速度在x 方向的分量平方的平均值 (A) m kT x 32=v (B) m kT x 3312=v (C) m kT x /32=v (D) m kT x /2=v2.一定量的理想气体贮于某一容器中,温度为T ,气体分子的质量为m 。
根据理想气体分子模型和统计假设,分子速度在x 方向的分量的平均值 (A) m kT π8=x v (B) m kT π831=x v (C) m kT π38=x v (D) =x v 03.温度、压强相同的氦气和氧气,它们分子的平均动能ε和平均平动动能w 有如下关系:(A) ε和w都相等 (B) ε相等,w 不相等 (C) w 相等,ε不相等 (D) ε和w 都不相等4.在标准状态下,若氧气(视为刚性双原子分子的理想气体)和氦气的体积比V 1 / V 2=1 / 2 ,则其内能之比E 1 / E 2为:(A) 3 / 10 (B) 1 / 2 (C) 5 / 6 (D) 5 / 35.水蒸气分解成同温度的氢气和氧气,内能增加了百分之几(不计振动自由度和化学能)?(A) 66.7% (B) 50% (C) 25% (D) 06.两瓶不同种类的理想气体,它们的温度和压强都相同,但体积不同,则单位体积内的气体分子数n ,单位体积内的气体分子的总平动动能(E K /V ),单位体积内的气体质量ρ,分别有如下关系:(A) n 不同,(E K /V )不同,ρ不同 (B) n 不同,(E K /V )不同,ρ相同(C) n 相同,(E K /V )相同,ρ不同 (D) n 相同,(E K /V )相同,ρ相同7.一瓶氦气和一瓶氮气密度相同,分子平均平动动能相同,而且它们都处于平衡状态,则它们(A) 温度相同、压强相同 (B) 温度、压强都不相同(C) 温度相同,但氦气的压强大于氮气的压强(D) 温度相同,但氦气的压强小于氮气的压强8.关于温度的意义,有下列几种说法:(1) 气体的温度是分子平均平动动能的量度;(2) 气体的温度是大量气体分子热运动的集体表现,具有统计意义;(3) 温度的高低反映物质内部分子运动剧烈程度的不同;(4) 从微观上看,气体的温度表示每个气体分子的冷热程度。
大学物理-热学习题课(ppt模板)

(二)热力学 1、功、热量、内能 W PdV (过程量)
Q Mc T2 T1 (过程量) M E T CVm T2 T1 (状态量)
2、热力学第一定律及其应用 等值过程 Q, E 和 W 的计算 见附表
附表:
Q
等温 过程 等压 过程 等体 过程
V2 M RT ln V1 M CP,m T M CV ,m T
(2)从状态B到达状态C,气体的熵变为 TC dQ TC C pdT TC 5 R 9 SBC C p ln ln TB T TB T TB 2 2
2.5 8.31 1.504 31.25 J K
1
得 T 274.37K
熵变:0C 冰
0C 水
dQ 1 S1 dQ T T 1 1 m2 L 12.23J K T 0C 的水 274.37 K 的水 m2 c2 dT dQ S 2 T T T 1 m2 c 2 ln 0.21J K T1
T2 卡诺逆循环 T1 T2
Q1
Q1
4、热力学第二定律的两种表述
克劳修斯 “热量不能自动的 从低温物体传向高温物体” 开尔文 “其唯一效果是热全部转 变为功的过程是不可能的” 5、可逆过程和不可逆过程 ★6、熵的计算与熵增加原理
dQ S 2 S1 T 可逆
三、计算 1、孤立系统中 m1 0.5kg, T1 276K
的水,和 m2 0.01kg, T2 273K 的冰 混合后冰全部融化 求(1)达到平衡时的温度 3 1 (2)系统的熵变( L 334 10 J kg ) 解:平衡时温度为 T
m1c1 T1 T m2 L m2 c2 T T2
大学物理-热学习题课和答案解析

2V
D)n 相同,(EK / V )相同,ρ相同。 nm 不同
8、给定理想气体,从标准状态( P0 V0 T0 )开始作绝热膨胀,
体积增大到3倍,膨胀后温度T, 压强P与标准状态时T0 、
P0的关系为:
√ A)T
(1) 3
T0
P
(1) 3
1
P0
B)T
(
1 3
)
1T0
P
(1) 3
P0
C)T
( 1 ) 3
了。则 根据热力学定律可以断定:
① 理想气体系统在此过程中吸了热。
② 在此过程中外界对理想气体系统作了功。 ③ 理想气体系统的内能增加了。 ④ 理想气体系统既从外界吸了热,又对外作了功。
√ A) ① ③ B) ② ③ C) ③ D) ③ ④ E) ④
7、两瓶不同种类的理想气体,它们的温度和压强都相同,但
i RT
2 ( E )
(Q) p Cp,mRT
(Q )T
RT
ln
V2 V1
( A)
Q0
E CV ,mT
pV
RT
CV ,m
iR 2
CP,m
CV ,m
R
i2 2
R
循环过程:
热机效率
卡诺热机效率
A Q吸 Q放 1 Q放
Q吸
Q吸
Q吸
卡 诺
A Q吸
1 Q放 Q吸
1 T2 T1
卡诺致冷系数
2kT m
2RT M mol
平均速率:
v 8kT 8RT
m
M mol
4、能量均分原理: 每一个自由度的平均动能为: 一个分子的总平均动能为: mol 理想气体的内能:
《大学物理学》热力学基础练习题
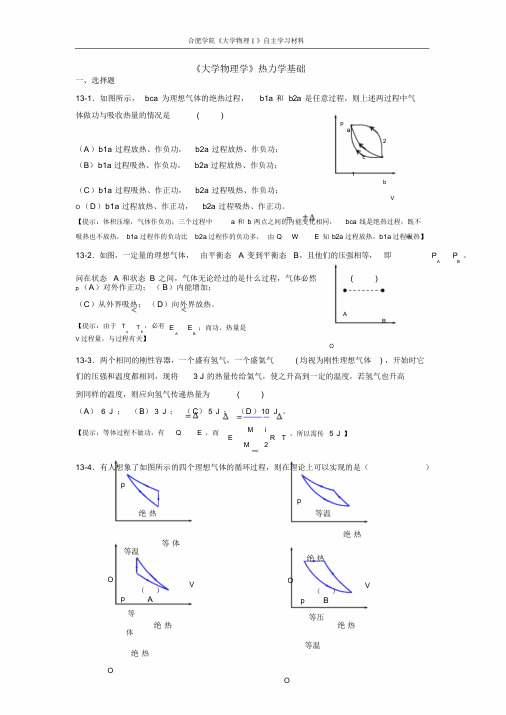
合肥学院《大学物理Ⅰ》自主学习材料《大学物理学》热力学基础一、选择题13-1.如图所示,bca 为理想气体的绝热过程,b1a 和b2a 是任意过程,则上述两过程中气体做功与吸收热量的情况是( )pa2(A)b1a 过程放热、作负功,b2a 过程放热、作负功;c(B)b1a 过程吸热、作负功,b2a 过程放热、作负功;1b(C)b1a 过程吸热、作正功,b2a 过程吸热、作负功;VO (D)b1a 过程放热、作正功,b2a 过程吸热、作正功。
【提示:体积压缩,气体作负功;三个过程中 a 和b 两点之间的内能变化相同,bca 线是绝热过程,既不吸热也不放热,b1a 过程作的负功比b2a 过程作的负功多,由Q W E 知b2a 过程放热,b1a 过程吸热】13-2.如图,一定量的理想气体,由平衡态 A 变到平衡态B,且他们的压强相等,即P P 。
A B问在状态 A 和状态 B 之间,气体无论经过的是什么过程,气体必然( )p (A)对外作正功;(B)内能增加;(C)从外界吸热;(D)向外界放热。
AB【提示:由于T T ,必有A B E E ;而功、热量是A BV 过程量,与过程有关】O13-3.两个相同的刚性容器,一个盛有氢气,一个盛氦气( 均视为刚性理想气体) ,开始时它们的压强和温度都相同,现将 3 J 的热量传给氦气,使之升高到一定的温度,若氢气也升高到同样的温度,则应向氢气传递热量为( )(A) 6 J ;(B)3 J ;(C)5 J ;(D)10 J 。
【提示:等体过程不做功,有Q E ,而M iE R TM 2mol,所以需传 5 J 】13-4.有人想象了如图所示的四个理想气体的循环过程,则在理论上可以实现的是()pp绝热等温绝热等体等温绝热Op 等()AV Op()B等压V 绝热绝热体等温绝热OOVV ()C()D【提示:(A) 绝热线应该比等温线陡,(B)和(C)两条绝热线不能相交】热力学基础-1合肥学院《大学物理Ⅰ》自主学习材料13-5.一台工作于温度分别为327℃和27℃的高温热源与低温热源之间的卡诺热机,每经历一个循环吸热2000J,则对外做功()(A)2000 J ;(B)1000 J ;(C)4000 J ;(D)500 J 。
(完整版)大学物理热学习题附答案

一、选择题1.一定量的理想气体贮于某一容器中,温度为T ,气体分子的质量为m 。
根据理想气体的分子模型和统计假设,分子速度在x 方向的分量平方的平均值 (A) m kT x 32=v (B) m kT x 3312=v (C) m kT x /32=v (D) m kT x /2=v2.一定量的理想气体贮于某一容器中,温度为T ,气体分子的质量为m 。
根据理想气体分子模型和统计假设,分子速度在x 方向的分量的平均值 (A) m kT π8=x v (B) m kT π831=x v (C) m kT π38=x v (D) =x v 03.温度、压强相同的氦气和氧气,它们分子的平均动能ε和平均平动动能w 有如下关系:(A) ε和w都相等 (B) ε相等,w 不相等 (C) w 相等,ε不相等 (D) ε和w 都不相等4.在标准状态下,若氧气(视为刚性双原子分子的理想气体)和氦气的体积比V 1 / V 2=1 / 2 ,则其内能之比E 1 / E 2为:(A) 3 / 10 (B) 1 / 2 (C) 5 / 6 (D) 5 / 35.水蒸气分解成同温度的氢气和氧气,内能增加了百分之几(不计振动自由度和化学能)?(A) 66.7% (B) 50% (C) 25% (D) 06.两瓶不同种类的理想气体,它们的温度和压强都相同,但体积不同,则单位体积内的气体分子数n ,单位体积内的气体分子的总平动动能(E K /V ),单位体积内的气体质量ρ,分别有如下关系:(A) n 不同,(E K /V )不同,ρ不同 (B) n 不同,(E K /V )不同,ρ相同(C) n 相同,(E K /V )相同,ρ不同 (D) n 相同,(E K /V )相同,ρ相同7.一瓶氦气和一瓶氮气密度相同,分子平均平动动能相同,而且它们都处于平衡状态,则它们(A) 温度相同、压强相同 (B) 温度、压强都不相同(C) 温度相同,但氦气的压强大于氮气的压强(D) 温度相同,但氦气的压强小于氮气的压强8.关于温度的意义,有下列几种说法:(1) 气体的温度是分子平均平动动能的量度;(2) 气体的温度是大量气体分子热运动的集体表现,具有统计意义;(3) 温度的高低反映物质内部分子运动剧烈程度的不同;(4) 从微观上看,气体的温度表示每个气体分子的冷热程度。
大学物理热学练习题及答案

大学物理热学练习题及答案第一题:一个物体的质量是1 kg,温度从20°C升高到30°C,如果物体的比热容是4200 J/(kg·°C),求物体吸收的热量。
解答:根据热量公式Q = mcΔθ,其中 Q 表示吸收的热量,m 表示物体的质量,c 表示比热容,Δθ 表示温度变化。
代入数据得:Q = 1 kg × 4200 J/(kg·°C) × (30°C - 20°C)= 1 kg × 4200 J/(kg·°C) × 10°C= 42,000 J所以物体吸收的热量为42,000 J。
第二题:一块金属材料的质量是0.5 kg,它的比热容是400 J/(kg·°C),经过加热后,材料的温度升高了60°C。
求该金属材料所吸收的热量。
解答:根据热量公式Q = mcΔθ,其中 Q 表示吸收的热量,m 表示物体的质量,c 表示比热容,Δθ 表示温度变化。
代入数据得:Q = 0.5 kg × 400 J/(kg·°C) × 60°C= 12,000 J所以金属材料吸收的热量为12,000 J。
第三题:一个热容为300 J/(kg·°C)的物体,吸收了500 J的热量后,温度升高了多少摄氏度?解答:根据热量公式Q = mcΔθ,其中 Q 表示吸收的热量,m 表示物体的质量,c 表示比热容,Δθ 表示温度变化。
将已知数据代入公式:500 J = m × 300 J/(kg·°C) × Δθ解方程得:Δθ = 500 J / (m × 300 J/(kg·°C))= 500 J / (m/(kg·°C)) × (kg·°C/300 J)= (500/300) °C≈ 1.67°C所以温度升高了约1.67°C。
大学物理热力学第一定律习题

热力学第一定律习题讨论★例题1 一些基本过程的Q 、W 、∆U 、∆H 计算过程W Q ∆U ∆H i.g. 自由膨胀0 0 0 0 i.g. 等温可逆 nRTln(V 2/V 1) W 0等压 理想气体可逆 任意物质 p ∆V=Q p -∆U p ∆V=Q p -∆U⎰21T T p dT C ⎰21T T p dT C ⎰21T T V dT CQ p -W⎰21T T p dT C ⎰21T T p dT C 等容 理想气体 可逆 任意物质0 0 ⎰21T T V dT C⎰21T T V dT C⎰21T T V dT C⎰21T T V dT C ⎰21T T p dT C∆U+V ∆pi.g. 绝热可逆 -∆U= γ--11122V p V p0 ⎰21T T V dT C ⎰21T T p dT C i.g. 多方可逆 δ--11122V p V p∆U+W ⎰21T T V dT C⎰21T T p dT C可逆相变 (等温等压) p e ∆V Q p Q p -W Q p 化学反应 (等温等压)p e ∆VQ pQ p -W= nRTH m r ∆-∆Q p =∑Φ∆iim f i H ,ν例题2 气体由温度T 1变至T 2,吸收热量Q ,不做其他功,试分别考虑下列六项热力学关系在甲、乙、丙、丁四种情况下是否成立? (甲) i.g. 等压过程 (乙) i.g. 等容过程 (丙) r.g. 等压过程 (丁) r.g.等容过程∆U=C V ∆T √ √ ⨯ √ ∆H=C p ∆T √ √ √ ⨯ ∆U=Q V ⨯ √ ⨯ √ ∆H=Q P √ ⨯ √ ⨯ ∆U=Q-W √ √ √ √ ∆H=∆(U+pV) √ √ √ √dV V U dT T U dU T V )()(∂∂+∂∂= i.g. T VU)(∂∂=0,dU=C V dTr.g. dV=0, dU=C V dT例题3 1 mol i.g.从0℃分别经等容和等压加热到100℃,两过程的终态是否相同?∆U 、∆H 、W 、Q 是否相等?(目的:说明i.g.的U 和H 仅是温度的函数,Q 和W 与过程有关)解:T 1=0℃, T 2=100℃等容过程1:dV=0W 1=0 Q 1=∆U 1=C V (T 2-T 1)∆H 1=C p (T 2-T 1)等压过程2:dp=0Q 2=∆H 2=C p (T 2-T 1)∆U 2=C V (T 2-T 1)W 2=Q 2-∆U 2= C p (T 2-T 1)- C V (T 2-T 1)=R(T 2-T 1)=p 2V 2-p 1V 1=∆(pV) 因此,两过程的终态不同。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.5 8.311.504 31.25 J • K1
3.6
Q1 Q2 35RT 4 (RT ln 3 23RT 4)
Q2 Q2 Q1 1 1 21.7% ?
Q1 Q2 1 Q2 Q1
21.7%
(2)从状态B到达状态C,气体的熵变为
SBC
TC dQ T TB
TC TB
C pdT T
C
p
ln
TC TB
5R ln 9 22
m2 c2 dT T
m2c2
ln
T T1
0.21J
K 1
276K的水 274.37K 的水
S3
dQ T1 m1c1dT T T2 T
m1c1 ln
T T2
12.38J
K 1
所以,系统的熵变
S S1 S2 S3 0.06J K 1 0
【习题】1mol理想气体,其等体摩尔热容量CV=3R/2,做 ABCDA循环,图中AB为等温线,已知A的状态量为p、V、T。 问:(1)该循环的效率?制冷系数?(2)从状态B到达状 态C,在该过程中气体的熵变为多少?
设容器中气体质量为M,有
∴
2
T
iR
1 M2 M i R T
2
2
由于 H2 He ,且 iH2 iHe
∴ THe TH2
3、 两瓶不同种类的气体, 它们压强和温度相同,但体 积不同,问它们单位体积分 子数是否相同?单位体积中气体质量是否相 同?单位体积中分子总平动动能是否相同?
讨论:T1=T2 , p1 p2
求(1)达到平衡时的温度
(2)系统的熵变( L 334103 J kg1) 解:平衡时温度为 T
m1c1T1 T m2L m2c2 T T2
得 T 274.37K
熵变:0C 冰 0C水
S1
dQ T
1 T
dQ
1 T
m2
L
12.23J
K
1
0C 的水 274.37K 的水
S2
dQ T
2
—质量为M的气体的内能
2、容器中装有理想气体,
容器以速率 v 运动,当容器突
然停止,则容器温度将升高。
若有两个容器,一个装有He,另一装有 H2气,如果它们以相同速率运动,当它们突 然停止时,哪一个容器的温度上升较高。
讨论:当容器突然停止时,气体分子的 定向运动转化为分子无规则热运动,使其内 能增加,从而温度升高.
解:(1)已知A态的温度为T,根据理想气体状态方程求出
B、C、D三个状态的温度。
p
AB等温过程: TB=TA=T
9
BC等压过程:
TC
T 2
CD等体过程:
TD
3T 2
B
C
3p
p
A
D
O
V
3V 2 V
1 Q2 1 RT ln 3 23RT 4 21.7%
Q1
35RT 4
Q2
RT ln 3 23RT 4
热学 习题课
一、 基本内容
( 一 )气体动理论
1、理想气体压强公式
p
1 nmv2 3
2 3
n
k
或 p nkT
2、理想气体温度公式 k 3 kT
3、能量按自由度均分定理 2
任一自由度平均动能 1 kT
理想气体内能 E i RT 2 E M i RT
E
M
i 2
R(T2
T1)
2
2
4、麦克斯韦速率分布
W Q1
1
Q2 Q1
卡诺循环 1 T2
T1
(2)逆循环 Q2 Q2
W Q1 Q2
卡诺逆循环 T2
T1 T2
4、热力学第二定律的两种表述
克劳修斯 “热量不能自动的 从低温物体传向高温物体”
开尔文 “其唯一效果是热全部转 变为功的过程是不可能的”
5、可逆过程和不可逆过程
★6、熵的计算与熵增加原理
又
由 p nkT
∵n ,
m
得 n1 n2
不同气体 m不同 ∴
1 2
单位体积中的分子总平动动能数 n k W
因 n1 n2 , k k2 则 W 1 W 2
4、系统吸热是否一定温度升高?
讨论:首先要明白 热量是热传递能量,而温度是系统热运 动程度的量度。因此,系统的温度变化与 热量传递无必然联系。
M
CVm
T2
T1 (状态量)
2、热力学第一定律及其应用
等值过程Q, E和 W 的计算
见附表
附表:
Q
等温 过程
等压 过程
等体 过程
绝热 过程
M RT ln V2
V1
M
CP,mT
M
CV ,mT
0
E
0
M
CV ,mT
M
CV ,mT
M
CV ,mT
W
M RT ln V2
V1
PV
0
M
CV ,mT
3、热循环
(1)正循环
S2 S1
dQ T 可逆
在孤立系统中 S 0
二、讨论
1、某刚性双原子理想气体,
温度为T,在平衡状态下,下
列各式的意义.
(1) 3 kT
2
(2) 2 kT
2
(3)
5 2
kT
—分子的平均平动动能 —分子的平均转动动能 —分子的平均总动能
(4) 5 RT —一摩尔气体分子的内能
2
(5) M 5 RT
(1)分布函数
f (v) dN Ndv
(2)分布函数物理意义及分布曲线的物理意
义。
vp
2kT 1.41 RT
m
(3)三种统计速率
v
8kT 1.59
m
RT
v2
3kT 1.73 RT
m
(二)热力学
1、功、热量、内能
W PdV (过程量)
Q Mc T2 T1 (过程量)
E
T
机的功率。由卡诺循环的致冷系数
e T2 Q2
T1 T2 W
所以 W
Q2
T1 T2 T2
Q2 2 104 J
T1 310K,T2 300K 则 W 667J
故所需最小功率为667W
(2)冬天将致冷机换向,使他从室外取
热传入室内(热泵)若室外温度为 ,
室内 3保oC持
,仍然27o用C 上面的空调所耗
功率,则每秒传入室内的热量是多少?
解:此时是把室外作为低温热 源,吸取低温热源的热量向室 内(高温热源)传递
已知 W 667J,T1 300K,T2 270K 由 e T2 Q2 T1 T2 W
Q2
W
T2 T1 T2
6000J
则每秒传入室内、计算 1、孤立系统中m1 0.5kg,T1 276K 的水,和m2 0.01kg,T2 273K 的冰 混合后冰全部融化
例等温膨胀过程 Q 0吸热, W 0 对
外作功而内能温度保持不变
又例绝热过程 dQ 0,但系统内能、
温度可以变化
5、(1)夏季的致冷空调(冷 泵),须将室内热量排到室外
设为2 104 J S ,1 若室内温度为 27oC
室外温度为 37o C ,求该致冷机所需最小功 率
解:致冷机所需最小功率,即为卡诺循环
