南航2015理论力学真题答案
力学试卷(A)答案
2015年全国CAP 考试力学试卷（A ）答案一、（10分）如题一图所示，长L 质量m 的匀质细棒可绕过其一端O 的水平轴无摩擦转动。
初始时棒在水平位置，自由下落转动到竖直位置。
试求：（1）细棒在竖直位置时的角速度；（2） 在竖直位置的细棒下端与放置在水平光滑桌面上的质量为m /3的滑块相碰，若碰后细棒静止，则滑块的速度υ是多少。
解：（1） 机械能守恒：22111232mL mgL ω=解得：ω=（2） 角动量守恒：21133mL mL ωυ=解得：υ=题一图智浪教育—普惠英才文库二、（10分）在离地面6000m 的高空大气层中，产生一个能量约为E = 3000MeV 快速运动的介子。
若介子静止时的能量E 0 = 100MeV ，固有寿命s 10260-⨯=τ，试求：（1）介子的动能和运动速度；（2）判断这个介子能否运动到地面解：（1）22E mc ==解得： 02900MeV k E E E =-=18s m 10996.2-⋅⨯=u（2）相对地面上观察者：介子的寿命：030ττ==运动距离： 6000m m 10798.14>⨯==τu s 地球结论：介子可以到达地面。
三、（10分） 一质量为m 的跳伞运动员从足够高的空中落下（将运动员视为质点，设初始速度为零并开始计时），假设运动员在下落过程中所受的空气阻力与速度成正比，方向与速度方向相反（即kv f -=，其中k 为常数；v 为运动员的速率）。
试求：（1）运动员的下落速度与时间的关系（2）运动员的下落极限速度（收尾速度）解： 建立向下为正方向的一维坐标系，运动员所满足的动力学方程：ma mg kv =-整理： dv kv a g dt m==- 积分： dv dt kv g m=-⎰⎰ 整理： ln()m kv g t A k m --=+ 解得： k t m mg v A e k-'=- 初始条件：00.t v ==时，解得： mg A k'= 运动员的下落速度与时间的关系： (1)k t m mg v e k-=- .t →∞对应运动员的落地速度（收尾速度）：mg v k=四、（10分）一质量为m 的小虫，相对以ω角速度转动的、半径为R 的圆盘，向外以匀加速度a 爬行。
2015-2018年南京航空航天大学考研试题815理论力学
l 30o
O r
第 3 题图
第 4 题 （25 分） 图示平面机构中，长度为 R 的曲柄 OA 以匀角速度 ω 绕 O 轴作定轴转动，连杆 AB
的两端分别与曲柄上的点 A 和轮轴的中心点 B 铰接，并带动轮轴沿水平直线轨道作纯滚 动，轮轴的外半径为 R，内半径为 R / 2 ，求曲柄 OA 运动到图示位置时轮轴上点 C 的速度 和加速度。
B
D
O
A CE
第 5 题图
第 6 题（20 分） 图示三孔拱桥，由构件 AEG、GHB、HIC 和 IKD 通过铰链连接而成，A、D 处为固
定铰支座，B、C 处为可动铰支座。在 G、H 和 K 处分别作用集中力 F1、F2 和 F3。结构 尺寸如图，不计拱桥自重及各处摩擦。试用虚位移原理求支座 C 处的约束力。
z
MO
F′R
OA
B
y
x
第 2 题图
科目代码：815 科目名称：理论力学 第 1 页 共 3 页
第 3 题 （25 分）
图示平面机构，带有滑槽的杆 AO 绕 A 轴 作定轴转动，AO 长为 l，通过固结在轮心上的 A 销钉 O 推动半径为 r 的圆轮在水平地面上作纯 滚动。已知在图示瞬时杆 AO 的角速度为 ω， 角加速度为 α，均为顺时针方向，杆 AO 与水 平线的夹角为 30°，求该瞬时轮 O 的角速度和 角加速度。
A
ω
30
R/2
R
O
B
B
C
第 4 题图
C 轮轴侧视图
科目代码：815 科目名称：理论力学 第 2 页 共 3 页
第 5 题（25 分） 如图所示，质量为 m、半径为 r 的均质圆轮 O 沿倾
A
(完整版)理论力学习题集册答案解析
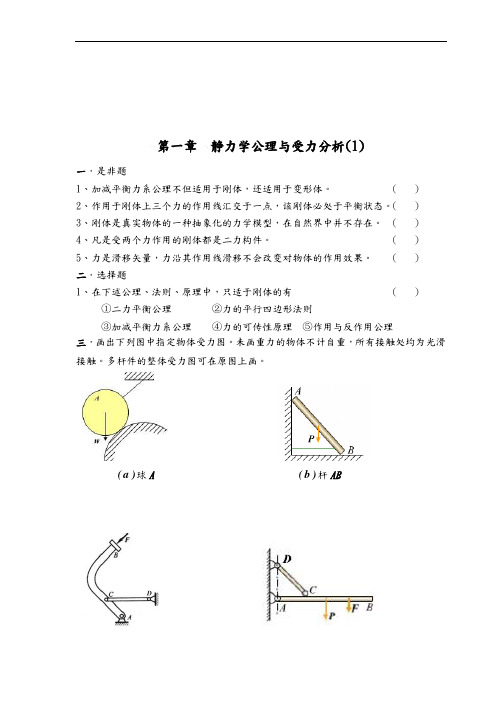
第一章静力学公理与受力分析(1)一．是非题1、加减平衡力系公理不但适用于刚体，还适用于变形体。
（）2、作用于刚体上三个力的作用线汇交于一点，该刚体必处于平衡状态。
（）3、刚体是真实物体的一种抽象化的力学模型，在自然界中并不存在。
（）4、凡是受两个力作用的刚体都是二力构件。
（）5、力是滑移矢量，力沿其作用线滑移不会改变对物体的作用效果。
（）二．选择题1、在下述公理、法则、原理中，只适于刚体的有（）①二力平衡公理②力的平行四边形法则③加减平衡力系公理④力的可传性原理⑤作用与反作用公理三．画出下列图中指定物体受力图。
未画重力的物体不计自重，所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
b(杆AB)a(球A )d(杆AB、CD、整体)c(杆AB、CD、整体))e(杆AC、CB、整体)f(杆AC、CD、整体四．画出下列图中指定物体受力图。
未画重力的物体不计自重，所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
)a(球A、球B、整体)b(杆BC、杆AC、整体第一章 静力学公理与受力分析（2）一．画出下列图中指定物体受力图。
未画重力的物体不计自重，所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
WADB CE Original FigureAD B CEWWFAxF AyF BFBD of the entire frame)a (杆AB 、BC 、整体 )b (杆AB 、BC 、轮E 、整体)c (杆AB 、CD 、整体 )d (杆BC 带铰、杆AC 、整体)e(杆CE、AH、整体)f(杆AD、杆DB、整体)g(杆AB带轮及较A、整体)h(杆AB、AC、AD、整体第二章平面汇交和力偶系一．是非题1、因为构成力偶的两个力满足F= - F’，所以力偶的合力等于零。
（）2、用解析法求平面汇交力系的合力时，若选用不同的直角坐标系，则所求得的合力不同。
（）3、力偶矩就是力偶。
（）二．电动机重P=500N，放在水平梁AC的中央，如图所示。
理论力学习题及答案(全)
第一章静力学基础一、是非题1．力有两种作用效果，即力可以使物体的运动状态发生变化，也可以使物体发生变形。
（）2．在理论力学中只研究力的外效应。
（）3．两端用光滑铰链连接的构件是二力构件。
（）4．作用在一个刚体上的任意两个力成平衡的必要与充分条件是：两个力的作用线相同，大小相等，方向相反。
（）5．作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
（）6．三力平衡定理指出：三力汇交于一点，则这三个力必然互相平衡。
（）7．平面汇交力系平衡时，力多边形各力应首尾相接，但在作图时力的顺序可以不同。
（）8．约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
（）二、选择题1．若作用在A点的两个大小不等的力F1和F2，沿同一直线但方向相反。
则其合力可以表示为。
①F1－F2；②F2－F1；③F1＋F2；2．作用在一个刚体上的两个力F A、F B，满足F A=－F B的条件，则该二力可能是。
①作用力和反作用力或一对平衡的力；②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶；④作用力和反作用力或一个力偶。
3．三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点；②共面三力若平衡，必汇交于一点；③三力汇交于一点，则这三个力必互相平衡。
4．已知F1、F2、F3、F4为作用于刚体上的平面共点力系，其力矢关系如图所示为平行四边形，由此。
①力系可合成为一个力偶；②力系可合成为一个力；③力系简化为一个力和一个力偶；④力系的合力为零，力系平衡。
5．在下述原理、法则、定理中，只适用于刚体的有。
①二力平衡原理；②力的平行四边形法则；③加减平衡力系原理；④力的可传性原理；⑤作用与反作用定理。
三、填空题1．二力平衡和作用反作用定律中的两个力，都是等值、反向、共线的，所不同的是。
2．已知力F沿直线AB作用，其中一个分力的作用与AB成30°角，若欲使另一个分力的大小在所有分力中为最小，则此二分力间的夹角为度。
南航理论力学习题答案14(1)
第十四章达朗贝尔原理1．平移刚体上的惯性力系向任意点简化，所得主矢相同，R Q ＝－m a C 。
设质心为C ，点O 到质心的矢径为r C ，则惯性力系向O 点简化的主矩为（ ）。
① ＭQO ＝0② ＭQO ＝J O α③ ＭQO ＝J C α④ ＭQO ＝r C ×R Q正确答案：④2．定轴转动刚体，其转轴垂直于质量对称平面，且不通过质心C ，当角速度ω＝0，角加速度α≠0时，其惯性力系的合力大小为R Q ＝ma C ，合力作用线的方位是（ ）。
（设转轴中心O 与质心C 的连线为OC ；J C 、J O 分别为刚体对质心及转轴中心的转动惯量）。
① 合力作用线通过转轴轴心，且垂直于OC② 合力作用线通过质心，且垂直于OC③ 合力作用线至轴心的垂直距离为h ＝J O α / ma C④ 合力作用线至轴心的垂直距离为h ＝OC ＋J C α / ma C正确答案：③、④3．刚体作定轴转动时，附加动反力等于零的充分必要条件是（ ）。
① 转轴是惯性主轴② 质心位于转轴上③ 转轴与质量对称面垂直④ 转轴是中心惯性主轴正确答案：④4．如图所示，质量为m 的质点A ，相对于半径为r 的圆环作匀速圆周运动，速度为u ；圆环绕O 轴转动，在图示瞬时角速度为ω，角加速度为α。
则图示瞬时，质点A 的惯性力为（ ）。
① )22(ωαu r m F gx +=)/2(22r u r m F gy +=ω② )22(ωαu r m F gx +−=)/2(22r u r m F gy +−=ω③ αmr F gx 2−=)22/(22ωωr u r u m F gy +−=④ 0=gx Fr mu F gy /2−=正确答案：③5．如图所示，半径为r ，质量为m 的均质圆盘与质量也为m 、长为l 的均质杆焊在一起，并绕O轴转动。
在图示瞬时，角速度为ω，角加速度为α 。
则惯性力系向O 点简化结果为（ ）。
① 2/)23(αm r l F g τ+=2/)23(2ωm r l F gn +=6/)1298(22αm lr r l M gO ++=② 2/)(αm r l F g τ+=2/)(2ωm r l F gn +=6/)1298(22αm lr r l M gO ++=③ 2/)23(αm r l F g τ+=2/)23(2ωm r l F gn +=2/)23(2αm r l M gO +=④ 2/)23(αm r l F g τ+=2/)23(2ωm r l F gn +=4/])(4[22αm r l l M gO ++=正确答案：①6．长度为r 的杆OA 与质量为m 、长度为2r 的均质杆AB 在A 端垂直固接，可绕轴O 转动。
理论力学复习题答案.doc
一、选择题1、A （4分）2、D （4分）3、B （4分）4、A （4分）二、填空题1、ωml 21，ω231ml 2、2243ωmR , ω223mR 3、 2/15三、判断题1、（ × ）2、（ √ ）3、（ √ ）四、计算题解：分别取CD 和整体为研究对象，列CD 杆平衡方程：02sin ,0=⨯-+⨯⇒=∑a F M a F M B C β （3分） )(5sin 2↑=-=KN aMF F B β(向上) （1分）列整体平衡方程：23sin 43,00sin ,00cos ,02=--++⇒=∑=+⨯-+⇒=∑=+⇒=∑qa Fa a F M M M F a q F F F F F F B A A NB AY Y AX X βββ （7分）将ο30,4,/1,.20,10=====βm a m KN q m KN M KN F 代入方程，联立求解，可得)(35←-=KN F AX (水平向右) ， )(4↑=KN F AY (铅直向上)， m KN M A .24= (逆时针) （4分）五、计算题解：动点：套筒A动系：固连在O 2B 上 （1分） 作速度平行四边形 （4分）r e a V V V += （2分）s cm V a /40=s rad A O /41=ω （3分）s cm V r /320= （2分）2/340s cm a C = （3分）六、计算题解: AB 作平面运动，以A 为基点，分析B 点的速度。
由图中几何关系得：(4分)(4分)(2分)B A BA =+r r rv v v cot30103cm/s B A v v ==o 20cm/s sin 30A BA vv ==o 1rad sBAAB v lω==方向如图所示。
七、计算题解：用动能定理求运动以杆为研究对象。
由于杆由水平位置静止开始运动，故开始的动能为零，即：01=T (1分)杆作定轴转动，转动到任一位置时的动能为222222181)32(1212121ωωml l l m ml J T O =⎥⎦⎤⎢⎣⎡-+==(1分) 在此过程中所有的力所作的功为ϕsin 6112mgl mgh W ==∑ (1分) 由2112T T W -=∑得22110sin 186ml mgl ωϕ-=23sin g l ωϕ=ω= (2分)将前式两边对时间求导，得：d 3d 2cos d d g t l tωϕωϕ= 3cos 2gl αϕ= (1分)A现求约束反力：质心加速度有切向和法向分量：tcos 4C g a OC αϕ=⋅=n2sin 2C g a OC ωϕ=⋅= (2分) 将其向直角坐标轴上投影得：t n3sin cos sin cos 4Cx C C ga a a ϕϕϕϕ=--=-t n23cos sin (13sin )4Cy C C g a a a ϕϕϕ=-+=-- (2分)由质心运动定理可得;,Cx x Cy y ma F ma F =∑=∑3sin cos 4Ox mgF ϕϕ-= 23(13sin )4Oy mg F mg ϕ--=- (3分)解得：3sin 28Ox mg F ϕ=-2(19sin )4Oy mgF ϕ=+ (2分)一、选择题（每题 4 分，共 16 分）1、A （4分）2、A （4分）3、C （4分）4、C （4分）二、填空题（每空 4 分，共 20 分）1、杆的动量为ωml 21，杆对O 轴的动量矩为ω231ml ， 2、 此瞬时小环M 的牵连加速度a e 为 2ωR ，小环M 科氏加速度a C 为 r V ω2 3、夹角θ应该满足的条件是 f φθ2≤三、判断题（每空 3 分，共 9 分）1、（ × ）2、（ √ ）3、（ √ ）四、计算题（共 15 分）解：）（↑=-⨯+⨯=kN 35)22(1M aqa a F a F B ；(5分) )(kN 40←==qa F Cx ，）（↑=-=-=kN 53540B Cy F F F ；(5分))(kN 80←=Ax F ，)(kN5↑=Ay F ，m kN 240⋅=A M （逆时针）。
南航理论力学习题答案7(1)
第七章刚体的简单运动1．刚体作平动时，刚体内各点的轨迹（）。
①一定是直线②一定是曲线③可以是直线，也可以是曲线④可以是直线，也可以是不同半径的圆正确答案：③2．某瞬时，刚体上任意两点A、B的速度分别为v A、v B，则下述结论正确的是（）。
①当v A = v B时，刚体必平动②当刚体作平动时，必有|v A| = |v B|，但v A与v B的方向有可能不同③当刚体作平动时，必有v A = v B④当刚体作平动时，v A与v B的方向必然相同，但可能|v A| ≠|v B|正确答案：③3．一对外啮合或内啮合的定轴传动齿轮，若啮合处不打滑，则任一瞬时两轮啮合点处的速度和加速度所满足的关系为（）。
①速度矢量和加速度矢量均相等②速度大小与加速度大小均相等③速度矢量和加速度矢量均不相等④速度矢量和切向加速度矢量均相等正确答案：④4．如图所示的平面机构中，三角板ABC与杆O1A、O2B铰接，若O1A = O2B = r，O2O1 = AB，则顶点C的运动轨迹为（）。
①以CO1长为半径，以O1点为圆心的圆②以CH长为半径，以H点为圆心的圆③以CD长（CD // AO1）为半径，以D点为圆心的圆④以CO = r长（CO // AO1）为半径，以O点为圆心的圆正确答案：④5．刚体绕定轴转动，（）。
①当转角ϕ>0时，角速度ω为正②当角速度ω>0时，角加速度α为正③当ω与α同号时为加速转动，当ω与α异号时为减速转动④当α>0时为加速转动，当α<0时为减速转动正确答案：③6．汽车左转弯时，已知车身作定轴转动，汽车左前灯A的速度大小为v A，汽车右前灯B的速度大小为v B。
A、B之间的距离为b，则汽车定轴转动的角速度大小为（）。
① b v A ② b v B ③ b v v B A )(+ ④ bv v B A )(− 正确答案：④7．每段长度相等的直角折杆在图示的平面内绕O 轴转动，角速度ω为顺时针转向，则M 点的速度方向如图中的（ ）所示。
南航理论力学习题答案17(1)
第十七章机械振动基础1．质量为m 的物体M ，置于光滑水平面上，在图示的连接情况下，系统的固有频率为（ ）。
① )(2121k k m k k + ② 2121)(k k k k m + ③m k k 21+ ④ 21k k m + 正确答案：①2．如图所示，在倾角为α的光滑斜面上，置一刚度系数为k 的弹簧，一质量为m 的物块沿斜面下滑s 距离与弹簧相碰，碰后弹簧与物块不分离并发生振动，则自由振动的固有频率为（ ）。
① mk ② ms k ③αsin m k ④ m k αsin 正确答案：①3．如图所示，单摆由无重刚杆OA 和质量为m 的小球A 构成。
小球上连接有两个刚度系数为k 的水平弹簧，则单摆微振动的固有频率为（ ）。
① mk ② m k 2 ③m k L g 2+ ④ m k L g + 正确答案：③4．图示的两个振动系统中，如果物块的质量和弹簧的刚度系数均相等，则此两种情况下系统的固有频率（ ）。
① 相同② 不同③ 由质量和刚度系数尚不能确定正确答案：①5．图示质量弹簧系统，已知物块的质量为m ，弹簧的刚度系数为k ，静伸长为δs ，原长是l 0 。
若以弹簧未伸长的下端点为坐标原点O ，则物块的运动微分方程为（ ）。
① 0=+x mk x ② 0)(=−+s x mk x δ ③ g x mk x s =−+)(δ ④ 0)(=++s x mk x δ 正确答案：②6．在图示中，当把弹簧原长的中点O 固定后，系统的固有频率与原来固有频率的比值为（ ）。
① 21 ② 2③ 2④ 4正确答案：③7．图示弹簧秤，秤盘重未知，当盘上放一重P 的物体时，测得振动周期为T 1；换一重Q 的物体时，其振动周期为T 2，则弹簧的刚度系数应为k =（ ）。
正确答案：)()(421222T T g P Q −−π8．图示为四根弹簧连接而成的振动装置，弹簧的刚度系数分别为k 1和k 2。
假设质量为m 的物块A 沿倾角为α的斜面作平动，则该振动装置的固有频率ω =（ ）。
理论力学习题答案
理论力学习题答案 Company number：【0089WT-8898YT-W8CCB-BUUT-202108】静力学第一章习题答案1-3 试画出图示各结构中构件AB 的受力图 1-4 试画出两结构中构件ABCD 的受力图1-5 试画出图a 和b 所示刚体系整体合格构件的受力图1-5a 1-5b1- 8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2，机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解：杆AB ，BC ，CD 为二力杆，受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压，分别选取销钉B 和C 为研究对象，受力如图所示： 由共点力系平衡方程，对B 点有： 对C 点有：解以上二个方程可得：22163.1362F F F ==解法2(几何法)分别选取销钉B 和C 为研究对象，根据汇交力系平衡条件，作用在B 和C点上的力构成封闭的力多边形，如图所示。
对B 点由几何关系可知：0245cos BC F F = 对C 点由几何关系可知： 0130cos F F BC解以上两式可得：2163.1F F =静力学第二章习题答案F 2F BC F AB B45oyx F BCF CDC60o F 130o xy F BC F CD 60o F 130o F 2F BC F AB 45o2-3 在图示结构中，二曲杆重不计，曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解：BC 为二力杆(受力如图所示)，故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用，A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示，由力偶系作用下刚体的平衡方程有（设力偶逆时针为正）： 其中：31tan =θ。
对BC 杆有：aM F F F A B C 354.0=== A ，C 两点约束力的方向如图所示。
(完整版)理论力学_习题集(含答案).doc
《理论力学》课程习题集西南科技大学成人、网络教育学院版权所有习题【说明】：本课程《理论力学》（编号为 06015）共有单选题 , 计算题 , 判断题 ,填空题等多种试题类型，其中，本习题集中有[ 判断题 ] 等试题类型未进入。
一、单选题1. 作用在刚体上仅有二力F A、 F B，且 F A F B 0 ，则此刚体________。
⑴、一定平衡⑵、一定不平衡⑶、平衡与否不能判断2. 作用在刚体上仅有二力偶，其力偶矩矢分别为M A、M B，且M A＋M B 0 ，则此刚体 ________ 。
⑴、一定平衡⑵、一定不平衡⑶、平衡与否不能判断3. 汇交于 O 点的平面汇交力系，其平衡方程式可表示为二力矩形式。
即m A F i 0 ，m B F i 0 ，但________。
⑴、 A 、 B 两点中有一点与O 点重合⑵、点 O 不在 A 、 B 两点的连线上⑶、点 O 应在 A 、 B 两点的连线上⑷、不存在二力矩形式，X 0, Y 0 是唯一的4. 力F在 x 轴上的投影为 F ，则该力在与x 轴共面的任一轴上的投影________ 。
⑴、一定不等于零⑵、不一定等于零⑶、一定等于零⑷、等于 F________。
5. 若平面一般力系简化的结果与简化中心无关，则该力系的简化结果为⑴、一合力⑵、平衡⑶、一合力偶⑷、一个力偶或平衡6.若平面力系对一点 A 的主矩为零，则此力系________。
⑴、不可能合成一个力⑵、不可能合成一个力偶⑶、一定平衡⑷、可能合成一个力偶，也可能平衡7.已知 F1、 F2、 F3、 F4为作用刚体上的平面共点力系，其力矢关系如图所示为平行四边形，因此可知________。
⑴、力系可合成为一个力偶⑵、力系可合成为一个力⑶、力系简化为一个力和一个力偶⑷、力系的合力为零，力系平衡8. 已知一平衡的平面任意力系F1、 F2F n1，如图，则平衡方程m A 0 ，m B 0 ，Y 0中（AB y ），有________个方程是独立的。
理论力学2015年南京航空航天大学硕士研究生考试真题
A
Oω α
R
C
D
M
B
第 3 题图
科目代码：815 科目名称：理论力学 第 1 页 共 3 页
梦想不会辜负每一个努力的人
a 0.9 m
第 4 题 （25 分）
图示平面机构中，已知圆轮 O 的半径为 0.5m，在 水平面上作纯滚动。连杆 AB 的两端分别与轮缘上的 A
A α ωO
点和滑块 B 铰接，并驱动滑块 B 沿水平面运动，图示
M
B
瞬时点 A 运动至最高点，轮 O 的角速度 ω =/s2。其它尺寸如图。试求：此时滑
1.2m
块 B 的速度和加速度。
第 4 题图
第 5 题（25 分）
图示系统位于铅垂面内，两匀质圆柱 O 和 C 的 质量均为 m、半径均为 r，其上缠有一细绳。质量为 m1 的物块 A 与绳的自由端相连，并可沿倾角为 的 光滑斜面滑动。假设绳 DE 段铅垂，绳 AB 段与斜面 平行，绳与两圆柱之间无相对滑动，不计绳重及轴承 摩擦。试求当 m = 3m1 时：（1）两圆柱的角加速度； （2）绳 AB 段的拉力。
质量为 46kg、半径为 0.5m，滑块 B 的质量为 17kg， 连杆 AB 的两端分别与轮缘上的 A 点和滑块 B 铰接， 圆轮 O 上作用有力偶 M，其它尺寸如图所示。若圆 轮 O 及滑块 B 与水平面间的静滑动摩擦因数均为 0.2，不计滚动摩阻、各铰链处的摩擦以及连杆 AB 的质量，求保持系统平衡的力偶 M 的最大值。
于铅垂位置，系统静止，现在杆 AB 的 B 端作用一大小为 I 的水平碰
撞冲量。试求碰撞结束时滑块 A 的速度。
IB
第 7 题图
科目代码：815 科目名称：理论力学 第 3 页 共 3 页
2002年~2013年南京航空航天大学理论力学考研试卷(整合)
a
A
y
D
q
南京航空航天大学
2012年硕士研究生入学考试初试试题（ A 卷）
科目代码： 815 科目名称： 理论力学 满分： 150 分
注意:①认真阅读答题纸上的注意事项；②所有答案必须写在答题纸上，写在本试题纸或草稿纸上均无效；③本试题纸须随答题纸一起装入试题袋中交回！
815 理论力学第 1 页共 2 页
815 理论力学第 2 页共 2 页
南京航空航天大学
2013年硕士研究生入学考试初试试题（ A 卷）
科目代码： 815 科目名称： 理论力学 满分： 150 分
注意:①认真阅读答题纸上的注意事项；②所有答案必须写在答题纸上，写在本试题纸或草稿纸上均无效；③本试题纸须随答题纸一起装入试题袋中交回！
科目代码：815 科目名称：理论力学第 1 页共 2 页
科目代码：815 科目名称：理论力学第 2 页共 2 页。
南航理论力学习题答案9(1)
第九章刚体的平面运动1．平面运动刚体相对其上任意两点的（ ）。
① 角速度相等，角加速度相等② 角速度相等，角加速度不相等③ 角速度不相等，角加速度相等④ 角速度不相等，角加速度不相等正确答案：①2．在图示瞬时，已知O 1A = O 2B ，且O 1A 与O 2 B 平行，则（ ）。
① ω1 = ω2，α1 = α2② ω1≠ω2，α1 = α2③ ω1 = ω2，α1 ≠α2④ ω1≠ω2，α1 ≠α2正确答案：③3．设平面图形上各点的加速度分布如图①~④所示，其中不可能发生的是（ ）。
正确答案：②4．刚体平面运动的瞬时平动，其特点是（ ）。
① 各点轨迹相同；速度相同，加速度相同② 该瞬时图形上各点的速度相同③ 该瞬时图形上各点的速度相同，加速度相同④ 每瞬时图形上各点的速度相同正确答案：②5．某瞬时，平面图形上任意两点A 、B 的速度分别v A 和v B ，如图所示。
则此时该两点连线中点C 的速度v C 和C 点相对基点A的速度v CA 分别为（ ）和（ ）。
① v C = v A + v B ② v C = ( v A + v B )/2③ v C A = ( v A - v B )/2 ④ v C A = ( v B - v A )/2正确答案：② ④α1α2 ①②③④6．平面图形上任意两点A 、B 的加速度a A 、a B 与连线AB 垂直，且a A ≠ a B ，则该瞬时，平面图形的角速度ω和角加速度α应为（ ）。
① ω≠0，α ≠0② ω≠0，α = 0③ ω = 0，α ≠0④ ω = 0，α = 0正确答案：③7．平面机构在图示位置时，AB 杆水平，OA 杆鉛直。
若B 点的速度v B ≠0，加速度τB a = 0，则此瞬时OA 杆的角速度ω和角加速度α为（ ）。
① ω = 0，α ≠0② ω≠0，α = 0③ ω = 0，α = 0④ ω≠0，α ≠0正确答案：②8．在图示三种运动情况下，平面运动刚体的速度瞬心：（a ）为（ ）；（b ）为（ ）；（c ）为（ ）。
南京航空航天大学考研历年真题之815理论力学2002--2015年真题
第 1 题 （25 分） 图示平面结构由杆 AEB、DC 和 BC 组成，尺寸如图，长度 a 为已知。在杆 AEB 的 AE 段受到均布载荷作用，载荷 集度为 q， 在杆 DC 上作用一力偶矩为 M 的力偶，且 M = qa2。各杆自重及各处摩 擦均不计。试求：支座 A、D 和 E 处的 约束力。 第 2 题 （15 分） 图示边长分别为 a、b、c 的长方体 受到由三个力构成的力系的作用，已知 F1 = Fi，F2 = 2Fj，F3= 3Fk， ，其中 i, j, k
A
第 4 题图
ϕ
O R r
第 5 题图
第 6 题（20 分） 如图所示，长为 l、质量为 m 的均质杆 AB，左端 A 为固定铰支座， 另一端用绳子 OB 拉住使其静止于水平位 置。已知：θ＝60°，不计各处摩擦及绳子的质量。用达朗 贝尔原理求突然撤去支座 A 的瞬时： （1）杆 AB 的角加速 度； （2）绳子 OB 的拉力。 第 7 题（15 分） 在图示平面机构中，杆 CD 上作用一力偶矩为 M 的力偶，滑块 E 可在铅垂槽中运动，其上作用一铅垂 方向的力 F， AD 连线铅直。 在图示位置机构处于平衡， 此时，杆 AB 水平，AC = CB = l，角度如图，不计各 构件和滑块的自重与各处摩擦。试用虚位移原理求此 时力偶矩 M 与力 F 之间的关系。
FP G1
R C
B G2 D
第 2 题图
第 3 题 （25 分） 图示平面机构，半径为 R 的圆环 C 固定，圆心 C 与 铰链 A 连线处于铅垂位置，杆 AB 绕定轴 A 转动，小圆环 M 套在杆 AB 和大圆环 C 上，已知杆 AB 的角速度和角加 速度分别为 ω 和 α 。试用点的合成运动方法，求杆 AB 与 水平线间的夹角ϕ =60 的瞬时，小环 M 的绝对速度和绝
南航理论力学习题答案
第十三章动 能 定 理1．如图所示，半径为R ，质量为m 1的均质滑轮上，作用一常力矩M ，吊升一质量为m 2的重物。
当重物上升高度h 时，力矩M 所作的功为（ ）。
① Mh /R② m 2gh③ Mh/R －m 2gh④ 0正确答案：①2．三棱柱B 沿三棱柱A 的斜面运动，三棱柱A 沿光滑水平面向左运动。
已知A 的质量为m 1，B 的质量为m 2；某瞬时A 的速度为v 1，B 沿斜面的速度为v 2。
则此时三棱柱B 的动能为 （ ）。
① 22221v m ② 2212)(21v v m − ③ )(2122212v v m − ④ ]sin )cos [(212222212θθv v v m +− 正确答案：④3．一质量为m ，半径为r 的均质圆轮以匀角速度ω沿水平面作纯滚动，均质杆OA 与圆轮在轮心O 处铰接，如图所示。
设OA 杆长l = 4r ，质量M = m /4。
在图示杆与铅垂线的夹角φ = 60°时，其角速度ωOA = ω/2，则此时该系统的动能为（ ）。
① 222425ωmr T =② 221211ωmr T = ③ 2267ωmr T = ④ 2232ωmr T = 正确答案：③4．均质圆盘A ，半径为r ，质量为m ，在半径为R 的固定圆柱面内作纯滚动，如图所示。
则圆盘的动能为（ ）。
① 2243ϕ mr T = ② 2243ϕ mR T = ③ 22)(21ϕ r R m T −= ④ 22)(43ϕ r R m T −= 正确答案：④5．图示均质圆盘沿水平直线轨道作纯滚动，在盘心移动了距离s 的过程中，水平常力F T 的功A T =（ ）；轨道给圆轮的摩擦力F f 的功A f =（ ）。
① F T s② 2F T s③ 0④ －F f s正确答案：② ③6．图示二均质圆盘A 和B ，它们的质量相等，半径相同，各置于光滑水平面上，分别受到F 和F ′的作用，由静止开始运动。
理论力学试题含答案
Fy 0 ， FAy FBy F 0
FAy 10kN
MA 0， MA M F 4 0
M A 35kN m
MA
A
FAx
FAy
M 4m
F
B FBy
FBx
二、OA 杆长 l1，绕 O 轴定轴转动，带动长为 l2 的套筒 AB 在 O1D 杆上滑动。若设置如图所示的参考基
墙壁滑动。在图示位置，圆盘的角速度为 ，角加速度为 ，杆与水平面的夹角为 ，试求该 B
瞬时杆端 B 的速度和加速度。
l
解：(1) 球速度，速度瞬心 C 如图
AC l sin ， BC l cos
r
vA r （2 分）
AB
vA AC
r l sin
（2
分）
A
vB
BC AB
l cos
r l sin
aB
1 sin
(r
cos
r 2 2 l sin2
)
r
cot
r 22 （2 l sin3
分）
.
C
AB
B
l
vB
r
A
aA
B
l
aA
A
AB
aBnA
aBt A
aB
四、图示系统，均质圆盘 O1 、O2 质量均为 m ，半径均为 R ， 圆盘 O2 上作用已知力偶 M，使圆盘绕 O2 轴转动，通过自重 不计的水平绳带动圆盘 O1 在水平面上纯滚。试完成： (1) 用拉格朗日方程求盘心 O1 的加速度； (2) 求水平绳的张力；
(3) 滑轮 O1 与地面的静摩擦力。 解：(1) 求加速度
选 O2 轮的转角2 为广义坐标
15秋西交《理论力学》在线作业答案
15秋西交《理论力学》在线作业答案15秋西交《理论力学》在线作业答案一、单选题（共10道试题，共20分。
）1.点作曲线运动时下列说法正确的是（）、A.若切向加速度为正，则点作加速运动B.若切向加速度与速度符号相同，则点作加速运动C.若切向加速度为零，则速度为常矢量D.以上说法都不正确正确答案：B2.一实心圆柱体，沿一斜面无滑动的滚下，下列说法正确的是（）、A.机械能守恒，动量矩不守恒B.质心动量守恒C.机械能不守恒，动量矩守恒D.没有守恒量正确答案：A3.刚体绕同平面内任意二根轴转动的合成运动（）、A.一定是平面运动B.一定是平动C.一定是定轴转动D.是绕瞬轴的转动正确答案：D4.一个均质实心球与一个均质实心圆柱在同一位置由静止出发沿同一斜面无滑动地滚下，则（）、A.圆柱先到达底部B.质量大的一个先到达底部C.半径大的一个先到达底部D.球先到达底部正确答案：D5.三力平衡定理是（）、A.共面不平行的三个力互相平衡必汇交于一点B.共面三力若平衡，必汇交于一点C.三力汇交于一点，则这三个力必互相平衡正确答案：A6.下述刚体运动一定是平动的是（）、A.刚体运动时，其上有不在一条直线上的三点始终作直线运动B.刚体运动时，其上所有的点到某固定平面的距离始终保护不变C.刚体运动时，其上有两条相交直线始终与各自初始位置保持平行D.刚体运动时，其上有不在一条直线上的三点的速度大小方向始终相同正确答案：D7.三棱柱重P，放在光滑的水平面上，重Q的匀质圆柱体静止释放后沿斜面作纯滚动，则系统在运动过程中（）、A.沿水平方向动量守恒，机械能守恒B.动量守恒，机械能守恒C.沿水平方向动量守恒，机械能不守恒D.均不守恒。
正确答案：A8.一动点作平面曲线运动，若其速率不变，则其速度矢量与加速度矢量（）、A.平行B.垂直C.夹角随时间变化D.不能确定正确答案：B9.点作匀变速曲线运动是指（）、A.点的加速度大小a=常量；B.点的加速度a=常矢量C.点的切向加速度大小为常量D.点的法向加速度大小为常量正确答案：C10.在有心力场中运动的质点，下列说法正确的是（）、A.动量守恒，角动量守恒，机械能守恒B.动量不守恒，角动量守恒，机械能守恒C.角动量不守恒。
理论力学试题第15套 参考答案word文档良心出品
.填空题（共6分，每空2 分）(1) a, b, d; (2) a, d; (3)a, d。
二.简答题（共14分）1.运动员起跑时，什么力使运动员的质心加速运动。
什么力使运动员的动能增加。
使运动员的质心加速运动的力是否一定做功。
（7分）答：起跑时，地面对运动员脚掌的摩擦力使其质心加速，但摩擦力作用点无位移，并不做功。
运动员的动能增加，是其体内肌肉内力做功的结果。
产生加速度的力并不一定做功，如纯滚动时地面的摩擦力，单摆的绳子拉力等。
2.花样滑冰运动员在光滑的冰面上，可做出许多优美的动作。
读者试分析运动员绕铅垂轴角速度的变化。
（7分）答：在光滑的冰面上，运动员的动量矩守恒，当运动员张开手臂时，运动员的转动惯量增加，则运动员转的慢，即运动员绕铅垂轴角速度的变小；收回手臂时，运动员的转动惯量减小，则运动员转的快，即运动员绕铅垂轴角速度的变大。
三.车床电动机的功率P=4.5kW ,当稳定运转时主轴的转速为n =42r/min ,设转动时，由于摩擦而损耗的功率是输入功率的30%，工件的直径d=100mm.求此转速下的切削力。
（20分）解：车床稳定运转时，器=0。
由功率方程知，输入功率与输出功率相等。
P输入=P有用+ P无用而P无用=0.3F输入，代入上式得P有用=0.7P输入=0.7咒4护1 0 g(3 1 W0 有用阻力就是切削力，P有用表示切削力的功率，即昭用=F v = F 100咒2兀X42=0.22FN m/s2 2X1000 60四.卷扬机的机构如图所示。
可绕固定轴转动的轮B和C,其半径分别为R和r,对自身转轴的转动惯量分别为J i和J2。
被提升重物A的重量为W，作用于轮C的主动转矩为M，求重物A的加速度。
（20分）解：由题可知，根据动量矩定理有:廿B（F）右M C(F)其中：L B=J^1+W V RgL c = J2⑷ 2F*M B(F) =FR -WRM c(F) =M -Fr根据运动学关系有：a = R&1 = r ^2整理后，得:2_ (M -Wr R rga " J1r 2^J2R2^WR2r2五.匀质细杆质量为m,长度OA=I，可绕水平轴0转动，如图所示。