大学物理—磁通量 磁场中的高斯定理
大学物理-7-3 磁通量 磁场的高斯定理

B
磁通量:通过某一曲面 的磁感线数为通过此曲面 的磁通量.
Φ BS cosBS
Φ B S B enS dΦ B dS
B dΦ BdS cos
s
Φ s BdS
单位 1Wb 1T 1m2
B dS1
1 B1
S
B2
2
dS2
dΦ1 B1 dS1 0 dΦ2 B2 dS2 0
SB cosdS 0
S B d S 0
3a
2a 5a
l
Φ s BdS = 0
I
磁场高斯定理
S B d S 0
物理意义:通过任意闭合曲面的磁通量必等于零。
(故磁场是无源的.)
求磁通量(1)用磁通量的定义求(2)用高斯定理求
例1 如图载流长直导线的电流为
积的磁通量.
解 先求
,试I 求 通过矩形面 ,B对变磁场给出
B
后积B 分dΦ求0I
2π x
Φ
B // S
I
l
d1 d2
dΦ BdS 0I ldx
Φ
S
B
dS
2π x
0Il
2π
d2
d1
dx x
o
x Φ 0Il ln d2
2π d1
例2 一半径为a的无限长直载流导线,沿轴向均
匀地流有电流I,若作一个半径为 R= 5a,高为l
的柱形曲面,已知此柱形曲面的轴与载流导线的 轴平行且相距3a(如图),则在圆柱侧面S上的 磁通量=?
第三节 磁场的高斯定理
一 磁感线
规定:曲线上每一点的切线方向就是该点的磁感
强度 B 的方向,曲线的疏密程度表示该点的磁感强 度 B 的大小.
I
大学物理课件:16-5 磁场的高斯定理和安培环路定理

B2
dl2
r2
l
B2
dl2
0I
2π
d
B1
dl1
0I
2π
d
B dl 0I d d
l
2π L1
L2
0I
2π
0
第16章 稳恒磁场
8
大学
16-5 磁场的高斯定理和安培环路定理
物理
多电流情况
I1
I2
I3
B
B1
B2
B3
Bdl
l
0 (I 2
I3)
以上结果对任意形状
l
的闭合电流(伸向无限远 的电流)均成立.
第16章 稳恒磁场
2
大学
16-5 磁场的高斯定理和安培环路定理
物理
enB
s s
B
磁通量:通过某一曲 面的磁感线数为通过此曲 面的磁通量.
Φ BS cosBS
Φ B S B enS
B dS
dΦ B dS
B dΦ BdS cos
s
Φ s BdS
单位 1Wb 1T 1m2
第16章 稳恒磁场
•
•
O’
磁场磁力线:
••••••••••••••
R
为什么磁力 线画成均匀 的?
B
• • • • • • • • • • • • • •
R
A B1 B
D
B2C
作安培环路L ABCDA
B dl
L
0
L内
Ii
0
B dl L
AB
B1
dl
B dl
BC
CD B2 dl
3
大学
16-5 磁场的高斯定理和安培环路定理
2、磁场的高斯定理和安培环路定理

L
B dl o I i
L
S
B dS 0 j dS
S
B 0 j
安培环路定理的物理意义 磁场是有旋场(或磁场是非保守场,磁感应线 是闭合曲线)。
三、安培环路定理的应用
O
R
r
例3、求长直螺线管内的磁场。设螺线管的长度为 L,共有N匝线圈,单位长度上有 n = N/L匝线圈, 通过每匝线圈电流为I。管内中间部分的磁场是均 匀的,方向与管的轴线平行,在管的外侧磁场很 弱,可以忽略不计。
B
a
b
c d [解]: 若螺线管很长,则边缘效应可以忽略,螺 线管可看成是无限长,由对称性可知管内磁场是 均匀的,方向与管的轴线平行,并由右手螺旋定 则确定。在管的外侧磁场很弱,可以忽略不计。
B dl B 2πr μ0 I ,
j I / R2
且 I j s jπr 2 (r <R)
B
1 B μ0 jr 2
μ0 Ir B 2π R 2
0 I B 2R
μ0 I r = R处 B 2π R
B
0 Ir 1 0 jr, ( r R) 2 2 R 2 0 I 1 R2 0 j , r R ) ( 2 r 2 r
例2、求均匀载流无限长圆柱导体内外的磁场分布。
[解]:当r R时 B dl B 2r 0 I
L
I
R
μ0 I B 2π r
I 由 j πR 2
1 R2 B μ0 j 2 r
(r >R)
I jπR2
r
L
L
大学物理-7-5磁通量磁场的高斯定理

第七章 恒定磁场
6
物理学
第五版
选择进入下一节:
本章目录
7-4 毕奥-萨伐尔定律 7-5 磁通量 磁场的高斯定理
7-6 安培环路定理
7-7 带电粒子在电场和磁场中的运动 7-8 载流导线在磁场中所受的力 7-9 磁场中的磁介质
第七章 恒定磁场
7
量必等于零(故磁场是无源的).
第七章 恒定磁场
5
物理学
第五版
7-5 磁通量 磁场的高斯定理
例 如图载流长直导线的电流为 I,试求
通过矩形面积的磁通量.
解 B 0I
B
2π x
dx
dΦBdS0I ldx
I
l
d1 d2
2πx
ΦSB dS20πIldd12dxx
ox
x Φ 0Il ln d2
磁通场过中的某磁点感处 线垂 数直 目等B 矢于量该的点单B 的位数面值积.上
第七章 恒定磁场
3
物理学
第五版
7-5 磁通量 磁场的高斯定理
B
磁通量:通过
en
某曲面的磁感线数
s
s
B
B dS
B
匀强磁场中,通 过面曲面S的磁通量:
Φ B SB enS
ΦBcSo sBS
物理学
第五版
7-5 磁通量 磁场的高斯定理
一 磁感线
切线方向—— 疏密程度——
B B的 的方 大向 小.;
I
I
I
第七章 恒定磁场
1
物理学
第五版
7-5 磁通量 磁场的高斯定理
I
S
I
S
毕奥-萨伐尔定律 磁通量 磁场的高斯定理
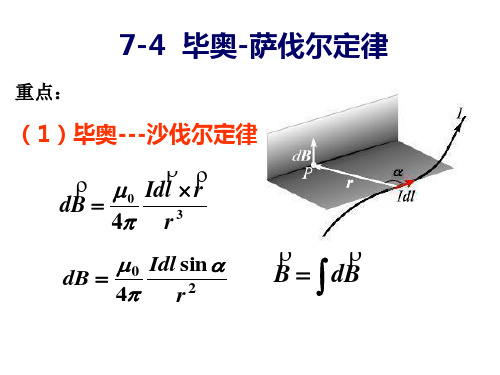
解:(1)判断电流元产生 每个电流元产生磁场同方向
磁场的方向是否一致
z
D
2
z r 0 cot
dz
I
z
1
r
r0
x
C
o
r0 dz d 2 sin dB r0 又r * y P sin 0 Idl sin (1) 大小 dB 2 4 r
B
0 I
2πr
I
B
I
X
B
电流与磁感强度成右手螺旋关系
2013-7-5
10
[例14-2] 圆电流轴线上的磁场。
0 Idl 解: dB sin 90 2 4 r 0 Idl B dB sin 90 2 4 r
x 因为圆线圈上各个电流元在P点产生的磁感应强度 的方向是不同的,所以只能用它的矢量表示:
第五版
四.运动电荷的磁场
7-4
毕奥-萨伐尔定律
考虑一段导体,其截面积为S,其 中载流子的密度为n,载流子带电 q,以漂移速度 v 运动。
毕奥—萨伐尔定律:
0 Idl r dB 4 π r3 0 nSdlqv r dB 3 4π r
P r dB Idl j Sdl nSdlqv
z
o
r
Idl
y
R
0 I dl sin x 2 2 2 r2 r R z 4 2 2 R 0 IR 0 I sin dl 3 2 0 2 2 4 r 2( R z ) 2
B
0 IR
2
2 2 32
2( R z )
7-5 磁通量 磁场的高斯定律7-6 安培环路定理

I1 I1
L
I2 I 3 I1
= −µ0 I1 + I2) (
问
v 1) B 是否与回路 L 外电流有关? 外电流有关? ) v v v 2)若 ∫ B ⋅ d l = 0 ,是否回路 L上各处 B = 0? ) L 内无电流穿过? 是否回路 L 内无电流穿过?
3、说明 、
•符号规定:电流方向与L的环绕方向服从右手关系的 I为正,否 符号规定:电流方向与 的环绕方向服从右手关系的 为正 为正, 符号规定 则为负。 则为负。 •安培环路定律对于任一形状的闭合回路均成立。 安培环路定律对于任一形状的闭合回路均成立。 安培环路定律对于任一形状的闭合回路均成立 •B的环流与电流分布有关,但路径上B仍是闭合路径内外电流的 的环流与电流分布有关,但路径上 仍是闭合路径内外电流的 的环流与电流分布有关 合贡献。 合贡献。 •物理意义:磁场是非保守场,不能引入势能。 物理意义:磁场是非保守场,不能引入势能。 物理意义
l MN
B ⋅ MN = µ 0 n MN I
B = µ 0 nI
无限长载流螺线管内部磁场处处相等 , 外部磁场 为零. 为零
例3 无限长载流圆柱体的磁场 解 1)对称性分析 2)选取回路 ) )
I
1)r > R
2π rB = µ0 I
v v ∫ B ⋅ d l = µ0 I
l
R R
L
r
2π r 2 v v πr 2)0 < r < R ∫ B ⋅ d l = µ0 2 I l πR 2 µ0r µ0 Ir 2π rB = 2 I B= 2 R 2π R
二、磁通量
1、磁通量定义: 、磁通量定义:
通过磁场中某一曲面的磁感应线的数目, 通过磁场中某一曲面的磁感应线的数目, 定义为磁通量, 表示。 定义为磁通量,用Ф表示。 表示
磁场中高斯定理公式(一)

磁场中高斯定理公式(一)
磁场中高斯定理公式
什么是磁场中高斯定理公式?
磁场中的高斯定理是电磁学中一个重要的定理,它描述了一个闭合曲面所围成的空间中的磁场总通量与该曲面上的磁场分布的关系。
根据磁场中的高斯定理公式,我们可以计算磁场通过一个封闭曲面的总磁通量。
高斯定理公式
高斯定理公式可以表示为:
∮B⋅dA=ΦB
其中, - $ $ 是磁感应强度(磁场向量), - $ $ 是封闭曲面上的面积微元(法向量), - $ _B $ 是磁场通过封闭曲面的总磁通量。
根据高斯定理,磁场通过一个封闭曲面的总磁通量等于磁场在该曲面上的散度。
示例解释
假设有一个半径为 $ R $ 的均匀磁场源,产生的磁感应强度为$ B $。
我们希望计算这个磁场通过一个半径为 $ r $ 的封闭曲面的总磁通量。
根据高斯定理公式,我们有:
∮B⋅dA=ΦB
根据对称性,磁场 $ $ 与面积微元 $ $ 的夹角为 0,因此上式可以简化为:
B⋅A=ΦB
其中, - $ A $ 是封闭曲面的面积。
由于磁场源是均匀的,磁感应强度 $ B $ 在封闭曲面上的每个面积微元 $ $ 上的取值都相同,因此可以提出来进行简化:
B⋅∫dA=ΦB
由于封闭曲面是一个圆柱体的侧表面,面积为 $ A = 2r L $,其中 $ L $ 是圆柱体的高度。
将这个表达式代入上式,可得:
B⋅2πrL=ΦB
总磁通量 $ _B $ 等于磁感应强度 $ B $ 乘以面积 $ 2r L $,即:
ΦB=2πrLB
这样,我们就计算出了磁场通过一个半径为 $ r $ 的封闭曲面的总磁通量。
磁高斯定理

磁高斯定理
磁高斯定理是一个重要的物理学理论,由哥本哈根大学的挪威物理学家,诺贝尔物理学家奥古斯特·磁高斯于1839年提出。
这个定理指出,任何给定的磁场,都可以由一个合适的磁向量场,即磁通量密度场来定义。
它表明,磁场是由磁向量场产生的,而不是由电荷分布引起的。
磁高斯定理的定义如下:对于任意闭合面S和其上的磁向量f,它们之间具有以下关系:
∫f•dl= ∫B•nds
其中f是内积,B是磁场,dl是封闭曲线的方向投影,nds是闭合面的法向量。
该定理的主要推论是,磁场的总流量,即数学上的积分,可以由已知的电荷分布来求得,而不必求出磁场本身。
这是一个非常重要的理论,因为它简化了对磁场的描述,而不必计算它的实际分布情况。
磁高斯定理表明,磁场是通过电流密度来描述的,而不是由电荷分布来描述。
这一定理最初是由磁高斯发现的,但是帕森斯在1860年重新分析并求得了该定理的希腊符号形式。
磁高斯定理在物理学,工程和其他应用领域有着广泛的应用,可以用来求出磁场的磁向量分布。
通过这种分布,我们可以知道磁场的方向和强度,从而估算磁场的复杂性。
此外,磁高斯定理在电力系统的设计以及磁学感测器的设计中也有重要的应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
S
磁场高斯定理
v v ∫S B ⋅d S = 0
物理意义: 物理意义:通过任意闭合曲面的磁通量必 等于零(故磁场是无源的 无源的) 等于零(故磁场是无源的).
补例: 补例: 如图载流长直导线的电流为I ,试求 通过矩形面积的磁通量. 通过矩形面积的磁通量 µ0 I 解 B= v B 2π x dx µ0I dΦ = BdS = ld x 2π x l I v v µ0 Il d2 dx Φ = ∫S B ⋅ dS = d1 ∫d1 d2 2π x o x µ 0 Il d 2 x
11.3 磁通量 磁场的高斯定理
一、磁场线(磁感应线 磁场线 磁感应线
1. 规定
磁力线) 磁力线)
v (1) 磁场线切线方向为磁感应强度 B的方向 v (2) 垂直 B的单位面积上穿过的磁场线条数为磁感 v 应强度 B 的大小
dN dΦm B= = dS ⊥ dS⊥
2. 磁场线的性质 (1) 无头无尾的闭合曲线 (2) 磁场线不相交
I
I
I
I S S N I N
二、磁通量
v en
v B
磁通量定义: 磁通量定义:通过某 曲面的磁感线条数。 曲面的磁感线条数。 1.匀强磁场中:通过面 匀强磁场中:通过面 匀强磁场中 曲面S的磁通量 曲面S的磁通量
s⊥
θ
s
v B
θ
v B
v dS
v θ B
v v v v Φ = B ⋅ S = B ⋅ enS
Φ = BS cosθ = BS⊥
2.一般情况: 一般情况: 一般情况
s
v v Φ = ∫s B ⋅ dSΒιβλιοθήκη dS2v BS2 θ
v dS1
θ1
v B1
v v dΦ1 = B1 ⋅ dS1 > 0
3. 闭合曲面: 闭合曲面:
v B2
v v dΦ2 = B2 ⋅ dS2 < 0
∫ B cos θ d S = 0
