抗弯矩形截面承载力计算表格(双筋)
双筋矩形梁正截面承载力计算讲解

双筋矩形梁正截面承载力计算一、双筋矩形梁正截面承载力计算图式二、基本计算公式和适用条件1.根据双筋矩形梁正截面受弯承载力的计算图式,由平衡条件可写出以下两个基本计算公式:由∑=0X 得:s y sy c A f A f bx f =''+1α 由∑=0M 得:)(2001a h A f x h bx f M M sy c u '-''+⎪⎭⎫ ⎝⎛-=≤α 式中'y f —— 钢筋的抗压强度设计值; 's A —— 受压钢筋截面面积;'a —— 受压钢筋合力点到截面受压边缘的距离。
其它符号意义同前。
2.适用条件 应用式以上公式时必须满足下列适用条件:(1)0h x b ξ≤ (2)'2a x ≥如果不能满足(2)的要求,即'2a x <时,可近似取'2a x =,这时受压钢筋的合力将与受压区混凝土压应力的合力相重合,如对受压钢筋合力点取矩,即可得到正截面受弯承载力的计算公式为:)(0a h A f M M s y u '-=≤当b ξξ≤的条件未能满足时,原则上仍以增大截面尺寸或提高混凝土强度等级为好。
只有在这两种措施都受到限制时,才可考虑用增大受压钢筋用量的办法来减小ξ。
三、计算步骤(一)截面选择(设计题)设计双筋矩形梁截面时,s A 总是未知量,而's A 则可能有未知或已知这两种不同情况。
1.已知M 、b 、h 和材料强度等级,计算所需s A 和's A (1)基本数据:c f ,y f 及'y f ,1α, 1β,b ξ(2)验算是否需用双筋截面由于梁承担的弯矩相对较大,截面相对较小,估计受拉钢筋较多,需布置两排,故取mm a 60=,a h h -=0。
单筋矩形截面所能承担的最大弯矩为:M bh f M b b c u <-=)5.01(201max 1ξξα,说明需用双筋截面。
第三章(5)双筋矩形截面梁
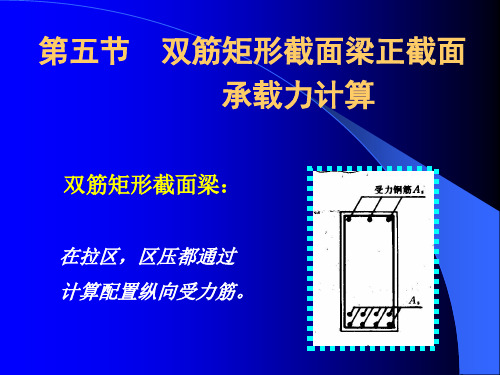
' s
M —— 外荷载所产生的弯矩设计值
M u —— 截面自身的抗弯承载力
T
—— 钢筋所受拉力
f y —— 钢筋抗拉强度设计值(屈服强度)
As —— 受拉钢筋截面面积
fc —— 砼的轴心抗压强度设计值。
b —— 梁截面宽
x
' s
—— 砼受压区高度
f y' —— 钢筋抗压强度设计值(屈服强度)
A —— 受压钢筋截面面积
3 22
2
25 250
例5、同上例,但事先给定压筋2 25 (As´ =982mm2), 求As。
x h0 h0
2
M f y´As (h´ a´ ) 0 s 2 f cm b
解:一、求x
219 106 310 982 (440 35) 440 4402 2 11 200 b h0 0.544 440 239(mm) 440 326 114(m m) 2as´ 2 35 70(mm)
2
11 200 440 0.544 (1 0.5 0.544) 168.7(kN m) M 219(kN m)
2
故应用双筋截面
二、求As´和As
M ´ s max bh0 f cm ´ As f y (h0 a s )
´
2
219 10 6 0.396 200 440 2 11 310 (440 35) 401(mm 2 )
' y ' s
1 fc b
2、求 若
' s
Mu
x ' ' ' f y As h0 as 2
双筋矩形截面正截面承载力计算公式及适用条件

表3.2.5 T形、I形及倒L形截面受弯构件翼缘计算宽度bf'
项次
考虑情况
1
按计算跨度l0考虑
2
按梁(纵肋)净距sn考虑
按翼缘 3 高度hf'
考虑
hf'/h0 ≥0.1 0.1 > hf'/h0 ≥0.05
hf'/h0 <0.05
T形截面、I形截面
肋形梁 肋形板
独立梁
l0/3
l0/3
b + sn
—
倒L形截面 肋形梁 肋形板
l0/6
b + sn/2
—
b + 12hf'
—
b + 12hf' b + 6hf' b + 5hf'
b + 12hf'
b
b + 5hf'
注:表中b为梁的腹板宽度。
2. T形截面的分类
第一类T形截面:中性轴通过翼缘,即x hf 第二类T形截面:中性轴通过肋部,即 x>hf
【解】查表得 fc=11.9N/mm2,ft=1.27N/mm2, fy=360N/mm2,α1=1.0,ξb=0.518
假定纵向钢筋排一层,则h0 = h-35 =400 -35 = 365mm, 1. 确定翼缘计算宽度
根据表3.2.5有: 按梁的计算跨度考虑: bf′ =l / 3=4800/3=1600mm 按梁净距sn 考虑:bf′=b+sn =3000mm 按翼缘厚度hf′考虑:hf′/h0 =80/365=0.219>0.1, 故不受此项限制。
【例3.2.6】某独立T形梁,截面尺寸如图3.2.13◆所示, 计算跨度7m,承受弯矩设计值695kN·m,采用C25级混凝 土和HRB400级钢筋,试确定纵向钢筋截面面积。
矩形梁抗弯抗剪计算
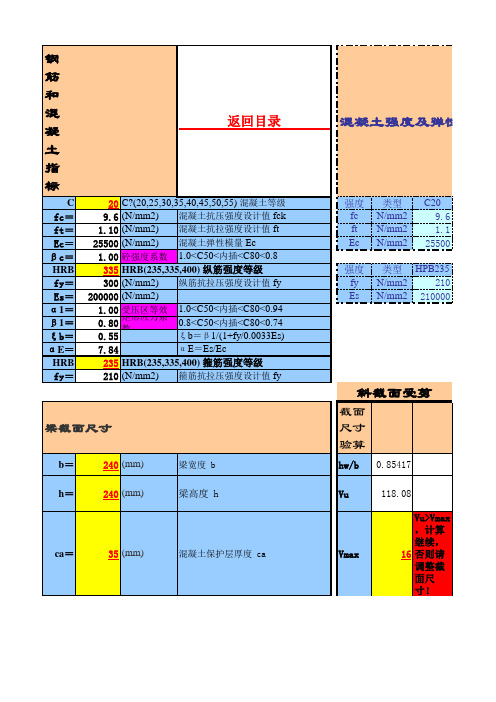
度及弹性模量
C25 11.9 1.27 28000 C30 14.3 1.43 30000 C35 16.7 1.57 31500 C40 C45 C50 C55 19.1 21.1 23.1 25.3 1.71 1.8 1.89 1.96 32500 33500 34500 35500
类型 HPB235 N/mm2 210 N/mm2 210000
斜截面受剪
梁截面尺寸
b= h= ca= h0= 240 (mm) 240 (mm) 35 (mm) 205 (mm)
梁宽度 b
截面尺寸验算
梁高度Байду номын сангаасh
混凝土保护层厚度 ca 梁有效高度 h0=h-ca
hw/b Vu Vmax S=
0.85417 118.08 16 Vu>Vmax,计算继续 80
均布荷载下只配箍筋计算
N= 实际配箍→ nAsv1/s -0.407 ρ sv 0.818% ρ svmin
正截面受弯
纵向钢筋:2φ 18
N= 2 纵筋根数 N φ= 18 (mm) 纵筋直径 φ As= 509 (mm2) 纵筋面积 As=N*(Pi*φ ^2/4) ρ= 1.03% 纵筋配筋率 ρ =As/(b*h0) Ny= 2 压筋根数 Ny φ y= 12 (mm) 压筋直径 φ y Asy= 226 (mm2) 压筋面积 Asy=Ny*(Pi*φ y^2/4) ρ y= 0.46% 压筋配筋率 ρ y=Asy/(b*h0) ξ = 0.180 相对受压区高度 ξ =ρ *fy/(α 1*fc) 注意:ξ <ξ b,将继续计算! x= 37 (mm) 受压区高度 x=ξ *h0 注意:x < 2ca,受压钢筋不屈服,取x=2ca=70(mm) 近似计算! 双筋矩形截面 抗弯承载力 Mu Mu= 26.0 (kN-m) 单筋矩形截面 抗弯承载力 Mu 15.8 (kN-m)
双筋矩形梁正截面承载力计算[整理版]
![双筋矩形梁正截面承载力计算[整理版]](https://img.taocdn.com/s3/m/742d15320622192e453610661ed9ad51f01d541e.png)
双筋矩形梁正截面承载力计算一、双筋矩形梁正截面承载力计算图式二、基本计算公式和适用条件1.根据双筋矩形梁正截面受弯承载力的计算图式,由平衡条件可写出以下两个基本计算公式:由∑=0X 得:s y sy c A f A f bx f =''+1α 由∑=0M 得:)(2001a h A f x h bx f M M sy c u '-''+⎪⎭⎫ ⎝⎛-=≤α 式中'y f —— 钢筋的抗压强度设计值;'s A —— 受压钢筋截面面积;'a —— 受压钢筋合力点到截面受压边缘的距离。
其它符号意义同前。
2.适用条件应用式以上公式时必须满足下列适用条件:(1)0h x b ξ≤(2)'2a x ≥如果不能满足(2)的要求,即'2a x <时,可近似取'2a x =,这时受压钢筋的合力将与受压区混凝土压应力的合力相重合,如对受压钢筋合力点取矩,即可得到正截面受弯承载力的计算公式为:)(0a h A f M M s y u '-=≤当b ξξ≤的条件未能满足时,原则上仍以增大截面尺寸或提高混凝土强度等级为好。
只有在这两种措施都受到限制时,才可考虑用增大受压钢筋用量的办法来减小ξ。
三、计算步骤(一)截面选择(设计题)设计双筋矩形梁截面时,s A 总是未知量,而's A 则可能有未知或已知这两种不同情况。
1.已知M 、b 、h 和材料强度等级,计算所需s A 和's A(1)基本数据:c f ,y f 及'y f ,1α, 1β,bξ(2)验算是否需用双筋截面由于梁承担的弯矩相对较大,截面相对较小,估计受拉钢筋较多,需布置两排,故取mm a 60=,a h h -=0。
单筋矩形截面所能承担的最大弯矩为:M bh f M b b c u <-=)5.01(201max 1ξξα,说明需用双筋截面。
矩形截面混凝土梁受弯计算表格
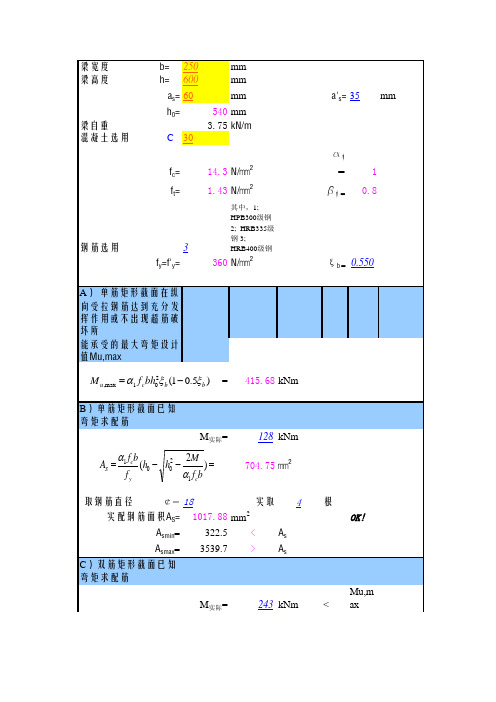
㎜2
20
¢=
8
mm >
根
2513.27 mm2 70 x
OK! NO!!!
验算受压区高度x=fyAs1/(α1fcb)=
360 N/㎜2
A) 单筋矩形截面在纵向受拉钢筋达到充分发挥作用或不出现超筋破坏所 能承受的最大弯矩设计值Mu,max
2 M u ,max = a1 f c bh0 x b (1 - 0.5x b )
=
415.68 kNm
B)单筋矩形截面已知弯矩求配筋 M实际= 128 kNm 704.75 ㎜2
AS =
纵向受拉钢筋总截面面积 As=As1+As2= 1999.51 ㎜2 受拉钢筋取钢筋直径
20¢=Biblioteka 2实取9 2
mm ≤
根
实配钢筋面积AS= 2827.43 mm 受压钢筋取钢筋直径 12 ¢= 实取 实配钢筋面积AS= 2α 's= 226.19 mm 70.00 mm
2
OK!
根
OK!
x
验算受压区高度x=fyAs1/(α1fcb)=
3
为充分发挥受压钢筋A's的作用,取As2=A's=
942.48 mm2
AS1 =
a1 fcb
fy
2 (h0 - h0 -
2M )= a1 fcb
-450.91 ㎜2
纵向受拉钢筋总截面面积 As=As1+As2= 受拉钢筋取钢筋直径 实配钢筋面积AS= 2α 's=
491.57 实取 -45.41 mm
a1 fcb 2M (h0 - h02 )= fy a1 fcb
¢=
取钢筋直径
18
1017.88 mm2 322.5
双筋矩形截面受弯构件正承载力计算讲解

二、双筋矩形截面受弯构件正承载力计算(一)计算简图在进行双筋矩形截面受弯构件正截面承载力计算时,计算简图如图3-19所示。
(二)基本公式(1)设计表达式根据图3-19所示的计算简图和内力平衡条件,可列出基本设计计算公式()⎥⎦⎤⎢⎣⎡'-''+⎪⎭⎫ ⎝⎛-=≤a h A f x h bx f M M 0s y 0c d d u 21γγ (3-14) s y s y c A f A f bx f ''-= (3-15)为了计算方便,将0h x ξ=代入式(3-14)、式(3-15),可得()[]a h A f bh f M M s s '-''+=≤0y 20c dd u 1αγγ (3-16) s y s y 0c A f A f h b f ''-=ξ (3-17) 式中 f y '——钢筋抗压强度设计值,按附录4表3取用;A's ——受压区纵向钢筋截面面积;a'——受压钢筋合力点至受压区边缘的距离。
(2)适用条件1)与单筋截面一样,为避免发生超筋情况,要求ξ≤ξb (3-18)2)保证受压钢筋应力能够达到抗压强度设计值,要求x ≥2a' (3-19)因为如果x 值太小,受压钢筋就太靠近中和轴,将得不到足够的变形,应力也就达不到抗压强度设计值,因而基本公式便不能成立。
双筋截面承受的弯矩较大,相应配置的受拉钢筋也较多,一般不必验算ρ≥ρmin 的条件。
(3)x <2a' 时的计算公式对于x <2a' 的情况,受压钢筋应力达不到f y '。
此时可近似假定受压钢筋的压力与受压混凝土的压力作用于同一直线上,且经过受压钢筋重心位置(图3-20)。
以受压钢筋合力点为力矩中心 ,可得()a h A f M M '-=≤0s y dd u 1γγ (3-20) 式(3-20)是双筋截面在x <2a' 时的唯一基本公式。
第五章受弯承载力计算双筋矩形截面

M 0
hf M u 1 f cbf hf (h0 ) 2
判别条件:
h xh f M a1 f cbf hf (h0 ) 第一类 T形截面 2
f
f
• 截面设计时:
h xh f M a1 f cbf hf ( h0 ) 第二类 T形截面 2 • 截面复核时:
解两个联立方程,求两个未知数x和As:
M u M u1 + M u 2 M u1 As f y (h0 as ) M u 2 M u M u1 x 1 f cbx(h0 ) 2
Mu2 x f y (h0 ) 2
由求出x ,然后由式出As2:
As 2
_ φ 受压钢筋选用3 20mm钢筋,As’=941mm2 。
求:所需受拉钢筋截面面积As
【解】
由附表(纵向受力钢筋的混凝土保护层最小厚度表)知,
环境类别为二级b,假定受拉钢筋放两排,设保护层
最小厚度35mm为故设α s=35+25/2=47.5mm,则
h0=400-47.5=352.5mm
由混凝土和钢筋等级,查附表(混凝土强
1)求计算系数:
M 330 106 s 2 1.0 19.1 200 4002 1 f cbh0
0.446
1 1 2 s 1 1 2 0.4 46
0.672>b 0.55
∴应设计成双筋矩形截面。
取ξ = ξ b,
M u 1 f cbh (1
1 f cbx
fy
1
而
As1
As f y fy
As f y + 1 f cbx fy
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
于在电脑上用Excel和在PDA上用Pocket Excel进行简单的结构手算,程序根据新规范编制,如有什么疑问请联系我,
制,如有什么疑问请联系我,以便立刻修正!
2。程序中黄底红字的部分需要使用者根据实际情况输入,黑色的部分请
情况输入,黑色的部分请不要随便更改,除非你发现有错误!
email:lingzhi0512@OICQ:49551484如需获
混凝土强度及弹性模量
强度 fc ft Ec 强度 fy Es C20 类型 N/mm2 9.6 N/mm2 1.1 N/mm2 25500 类型 HPB235 N/mm2 210 N/mm2 210000
梁截面尺寸
b= 250 (mm) 梁宽度 b (mm) h= 500 梁高度 h (mm) ca= 35 混凝土保护层厚度 ca (mm) h0= 465 梁有效高度 h0=h-ca 纵向钢筋:3φ22 N= 3 纵筋根数 N (mm) φ= 22 纵筋直径 φ (mm2) As= 1140 纵筋面积 As=N*(Pi*φ ^2/4) ρ= 0.98% 纵筋配筋率 ρ =As/(b*h0) Ny= 2 压筋根数 Ny (mm) φ y= 20 压筋直径 φ y (mm2) Asy= 628 压筋面积 Asy=Ny*(Pi*φ y^2/4) ρ y= 0.54% 压筋配筋率 ρ y=Asy/(b*h0) ξ = 0.092 相对受压区高度 ξ =ρ *fy/(α 1*fc) 注意:ξ <ξ b,将继续计算! x= 43 (mm) 受压区高度 x=ξ *h0 注意:x < 2ca,受压钢筋不屈服,取x=2ca=70(mm) 近似计算! Mu= 147.1 (kN-m) 抗弯承载力 Mu 说明: 1。若ξ >ξ b,则说明纵筋超筋,需要减少纵筋面积再进行计算! 2。若 x < 2ca,则说明当压区混凝土达到极限压应变是受压钢筋还 未屈服,这时取 x=2ca近似计算!
声明:
1。本程序为上海同济大学2003级结构工程李凌志编制整理,目的是为了便于在电脑上用Excel和在
强度及弹性模量
C25 C30 C35 11.9 14.3 16.7 1.27 1.43 1.57 28000 30000 31500 HRB335HRB400 300 360 200000 200000 C40 19.1 1.71 32500 C45 21.1 1.8 33500 C50 23.1 1.89 34500 C55 25.3 1.96 35500
OICQ:49551484如需获得更多E指标
C fc= ft= Ec= HRB fy= Es= α 1= β 1= ξ b= α E= 30 14.3 1.43 30000 335 300 200000 1.00 0.80 0.55 6.67 C?(20,25,30,35,40,45,50,55) 混凝土等级 (N/mm2) 混凝土抗压强度设计值 fck (N/mm2) 混凝土抗拉强度设计值 ft (N/mm2) 混凝土弹性模量 Ec HRB(235,335,400) 纵筋强度等级 (N/mm2) 纵筋抗拉压强度设计值 fy (N/mm2) 1.0<C50<内插<C80<0.94 0.8<C50<内插<C80<0.74 ξ b=β 1/(1+fy/0.0033Es) α E=Es/Ec
