平行四边形的性质练习题
平行四边形性质练习题(含答案)

平行四边形的性质练习1.在平行四边形ABCD 中,已知∠A =40°,则∠B = 140° , ∠C = 40° ,∠D = 140° .2.在□ABCD中,∠A :∠B =2:3,则∠B = 108° ,∠C = 72° ,∠D = 108° .3.若一个平行四边形相邻的两内角之比为2:3,则此平行四边形四个内角的度数分别为_72°、72°、108°和108°___.4.如图,在平行四边形ABCD 中,∠A -∠B =70º, 求平行四边形各角的度数。
∠A=∠C=125º∠B=∠D=55º5.如图,在□ABCD 中,∠B =120°,DE ⊥AB ,垂足为E ,DF ⊥BC ,垂足为F .求∠ADE ,∠EDF ,∠FDC 的度数.∠ADE=30º, ∠EDF=60º, ∠FDC=30º1、在□ABCD 中,已知AB =8,周长等于24,则BC = 4 ,CD = 8 ,AD = 4 .2、已知□ABCD 的周长为28cm ,AB :BC =3:4,则AB = 6 ,BC = 8 ,CD = 6 ,AD = 8 .3.在□ABCD 中,∠A =30°,AB =7 cm ,AD =6 cm ,则=____21___.4.平行四边形两邻边分别是4和6,其中一边上的高是3,则平行四边形的面积是_12或18_5.平行四边形邻边长是4 cm 和8cm ,一边上的高是5 cm ,则另一边上的高是__2.5__.6.已知:如图,四边形(1)说明(2)(1)CE=CF (2)CE 和CF1.一个平行四边形的一边长是8,一条对角线长是6,则它的另一条对角线x 的取值范围为_10<X<22____.2.□ABCD 中,周长为20cm ,对角线AC 交BD 于点O ,△OAB 比 △OBC 的周长多4,则边AB =___7___,BC =__3___.3.平行四边形的边长等于5和7,这个平行四边形锐角的平分线把长边分成两条线段长各是_5和2__.A DB C4.□ABCD中,对角线AC长为10 cm,∠CAB=30°,AB长为6 cm,则□ABCD的面积是__30cm2___.5.如图,在□ABCD中,已知对角线AC和BD相交于点O,ΔAOB 的周长为15,AB=6,那么对角线AC和BD的和是多少?AC+BD=186.如图,已知□ABCD的周长为60 cm,对角线AC、BD相交于点O,△AOB的周长比△BOC的周长长8cm,求这个四边形各边长.AB=CD=19AD=BC=11 7.如图,如果△AOB与△AOD的周长之差为8,而AB∶AD=3∶2,那么□ABCD的周长为多少?□ABCD的周长为808.已知,如图,在△ABC中,BD是∠ABC的平分线,DE∥BC交AB 于E,EF∥AC交BC于F,则BE=FC,为什么?BE=DE=FC。
平行四边形的性质

练习:如图、四边形ABCD和四边形AFCD都是平行四边形。
1、BE CF 2 、若B、E、F、C在同一直线上,当AF DE于G,
AG=3,DG=4,EF=10,S
ABCD
36.求DEC的面积
作业:《课外能力训练》 家作:《名校1号》上的题
例8、如图:在 ABCD中,对角线AC=21,BE AC,
垂足为点E,且BE=5cm,AD=7cm.求AD和BC之间的距离。
见《天府数学同步练习 册》P40的8、9两题
例9、如.
1、求证:CD AF ; 2 、若BC=2CD,求证:F=BCF
例7、如图 ABCD的对角线AC与BD相交于点O,其周长为16, 且AOB的周长比BOC的周长小2。求边AB和BC的长
变式练习1:如图 ABCD的对角线AC与BD相交于点O, AB AC,若AB=4,AC=6,则BD的长是
变式练习2:已知 ABCD的周长为42cm, 对角线AC、BD交于点O, AOB与BOC的周长 相差3cm, 求这个平行四边形各边的长
(完整版)平行四边形的性质判定练习题

第一部分 平行四边形的性质练习题 例题1、平行四边形得周长为50cm ,两邻边之差为5cm,求各边长。
变题1.平行四边形ABCD 的周长为40cm,两邻边AB 、AC 之比为2:3,则AB=_______,BC=________. 变题2.四边形ABCD 是平行四边形,∠BAC=90°,AB=3,AC=4,求AD 的长。
例题2.平行四边形ABCD 中,∠A-∠B=20°,求平行四边形各内角的度数。
变题3.平行四边形ABCD 中,AE 平分∠DAB, ∠DEA=20°,则∠C=_________,∠B_________. 变题4.如图,在平行四边形ABCD 中,∠BAC=34°, ∠ACB=26°,求∠DAC 与∠D 的度数。
例题3.如图,在平行四边形ABCD 中,CE ⊥AD,CF ⊥BA 交BA 的延长线于F ,∠FBC=30°,CE=3cm,CF=5cm,求平行四边形ABCD 的周长。
变题5.如图,平行四边形ABCD 的周长为50,其中AB=15,∠ABC=60°,求平行四边形面积。
1、如图,四边形ABCD 是平行四边形,AB=6cm,BC=8cm ,∠B=70°,则AD=________,CD=______,∠D=_______,∠A=______,∠C=_______.2、平行四边形ABCD 的周长为40cm,两邻边AB 、AC 之比为2:3,则AB=_______,BC=________.3、平行四边形得周长为50cm ,两邻边之差为5cm,则长边是________ ,短边是__________.4、平行四边形ABCD 中,∠A-∠B=20°, 则∠A=_______ ∠B=________5、.平行四边形ABCD 中,AE 平分∠DAB, ∠DEA=20°,则∠C=____,∠B_____.6、平行四边形 ABCD 中,∠A+∠C=200°.则:∠A= _______,∠B= _________ .7、如图,平行四边形ABCD 的周长为50,其中AB=15,∠ABC=60°,求平行四边形面积。
八年级数学下册平行四边形的性质练习题

八年级数学下册平行四边形的性质练习题(含答案解析)学校:___________姓名:___________班级:___________一、填空题1.在平行四边形ABCD 中,AB =3,BC =4,则平行四边形ABCD 的周长等于 _____.2.如图,等腰△ABC 中,△BAC =120°,点D 在边BC 上,等腰△ADE 绕点A 顺时针旋转30°后,点D 落在边AB 上,点E 落在边AC 上,若AE =2cm ,则四边形ABDE 的面积是__________.3.定义:一个三角形的一边长是另一边长的2倍,这样的三角形叫做“倍长三角形”.若等腰△ABC 是“倍长三角形”,底边BC 的长为3,则腰AB 的长为______.4.如图,已知DG △BC ,AC △BC ,CD △AB ,EF △AB ,则DG 与AC 间的距离是线段________的长,CD 与EF 间的距离是线段________的长.5.如图,平行四边形的中心在原点,AD BC ∥,D (3,2),C (1,﹣2),则A 点的坐标为________,B 点的坐标为________.6.如图,在平面直角坐标系中,点()1,2A -,4OC =,将平行四边形OABC 绕点O 旋转90°后,点B 的对应点B '坐标是______.7.如图,菱形ABCD 中,∠ABD=30°,AC=4,则BD的长为_______.8.如图,在直角坐标系中,平行四边形ABCD的BC边在x轴上,点A(0,3),B(−1,0),若直线y=−2x+4恰好平分平行四边形ABCD的面积,则点D的坐标是______.二、单选题9.如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE中点,且△ABC的面积等于4cm2,则阴影部分图形面积等于().A.1cm2B.2cm2C.0.5cm2D.1.5cm210.已知三角形的三边长分别为2、x、8,则x的值可能是()A.4B.6C.9D.1011.已知A、B、C三点不在同一条直线上,则以这三点为顶点的平行四边形共有()A .1个B .2个C .3个D .4个12.已知某点阵的第△△△个图如图所示,按此规律第( )个点阵图中,点的个数为2022个.A .1009B .2018C .2022D .2048三、解答题13.如图,PBD △和PAC △都是直角三角形,90DBP CAP ∠=∠=︒.(1)如图1,PA ,PB 与直线MN 重合,若45BDP ∠=︒,30ACP ∠=︒,求DPC ∠的度数;(2)如图2,若45BDP ∠=︒,30ACP ∠=︒,PBD △保持不动,PAC △绕点P 逆时针旋转一周.在旋转过程中,当PC BD ∥时,求APN ∠的度数;(3)如图3,()90180BPA a α∠=︒<<︒,点E 、F 分别是线段BD 、AC 上一动点,当PEF 周长最小时,直接写出EPF ∠的度数(用含α的代数式表示).14.在四边形ABCD 中,BAD ∠的平分线AF 交BC 于F ,延长AB 到E 使BE FC =,G 是AF 的中点,GE 交BC 于O ,连接GD .(1)当四边形ABCD 是矩形时,如图,求证:△GE GD =;△BO GD GO FC ⋅=⋅.(2)当四边形ABCD 是平行四边形时,如图,(1)中的结论都成立,请给出结论△的证明.15.如图,已知,AF DE AE FD ==,点B 、C 在AD 上,AB CD =,BF CE =.(1)图中共有__________对全等三角形;分别是__________;(2)我会说明__________≌△__________.(写出证明过程)参考答案:1.14【分析】由平行四边形的对边相等即可求得其周长.【详解】解:△四边形ABCD是平行四边形,△AB=CD,BC=AD,△平行四边形的周长为=2(AB+BC)=2×(3+4)=14,故答案为:14.【点睛】本题考查平行四边形的性质,熟知平行四边形的对边相等是解答的关键.22.【分析】如图,作AH△BC于H.证明四边形ABDE是平行四边形即可解决问题.【详解】解:如图,作AH△BC于H.由题意得:△EAD=△BAC=120°,△EAC=△C=30°,△AE△BC,△△ADH=△B+△BAD,△B=△BAD=30°,△△ADH=60°,BD=AD=AE=2cm,△AHcm),△BD=AE,BD△AE,△四边形ABDE是平行四边形,△SABCD=BD•AH cm2).2.故答案为【点睛】本题考查旋转变换,等腰三角形的性质,平行四边形的判定和性质等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题.3.6【分析】分类讨论:AB =AC =2BC 或BC =2AB =2AC ,然后根据三角形三边关系即可得出结果.【详解】解:△△ABC 是等腰三角形,底边BC =3△AB =AC当AB =AC =2BC 时,△ABC 是“倍长三角形”;当BC =2AB =2AC 时,AB +AC =BC ,根据三角形三边关系,此时A 、B 、C 不构成三角形,不符合题意; 所以当等腰△ABC 是“倍长三角形”,底边BC 的长为3,则腰AB 的长为6.故答案为6.【点睛】本题考查等腰三角形,三角形的三边关系,涉及分类讨论思想,结合三角形三边关系,灵活运用分类讨论思想是解题的关键.4. CG DE【分析】根据平行线间的距离等于平行线间任意一条垂线段的长度即可解题.【详解】解:由题可知:DG△AC,CD△EF,△DG 与AC 间的距离是线段CG ,CD 与EF 间的距离是线段DE.【点睛】本题考查了平行线之间的距离,属于简单题,找到平行线之间的垂线段是解题关键.5. (﹣1,2) (﹣3,﹣2)【分析】根据“关于原点对称的点横坐标互为相反数,纵坐标也互为相反数”即可解答.【详解】解:因为平行四边形是中心对称图形,而平行四边形的中心在原点,则A 点的坐标为(﹣1,2),B 点的坐标为(﹣3,﹣2).故答案为:(﹣1,2),(﹣3,﹣2).【点睛】本题主要考查了关于原点对称的点的坐标特征,熟练掌握关于原点对称的点横坐标互为相反数,纵坐标也互为相反数是解题的关键.6.()2,3-或()2,3-【分析】根据旋转可得: BM = B 1M 1 = B 2M 2 = 3,△AOA 1 =△AOA 2 = 90°,可得B 1和B 2的坐标,即是B '的坐标.【详解】解:△A (-1,2), OC = 4,△ C (4,0),B (3,2),M (0,2), BM = 3,AB//x轴,BM= 3.将平行四边形OABC绕点O分别顺时针、逆时针旋转90°后,由旋转得:OM=OM1=OM2=2,△AOA1=△AOA2=90°BM=B1M1=B2M2=3,A1B1△x轴,A2B2△x轴,△B1和B2的坐标分别为:(-2,3),(2,-3),△B'即是图中的B1和B2,坐标就是,B' (-2,3),(2,-3),故答案为:(-2,3)或(2,-3).【点睛】本题考查了平行四边形的性质,坐标与图形的性质,旋转的性质,正确的识别图形是解题的关键.7.【分析】根据菱形的性质可得△ABO=30°,AO=12AC=2,根据含30°角的直角三角形的性质及勾股定理即可求得BO的长,从而得到结果.【详解】如图:在菱形ABCD中,AC、BD是对角线,设相交于O点,△ABD=30°,AC=4,△AC△BD,AO=12AC=2,△AB=2AO=4,△BO,22BD BO∴==⨯=故答案为:【点睛】本题考查的是菱形的性质,解答本题的关键是熟练掌握菱形的对角线互相垂直平分,对角线平分对角.8.(72,3)【分析】连接BD,设D(m,3),BD的中点为T.求出点T的坐标,利用的待定系数法,可得结论.【详解】解:连接BD,设D(m,3),BD的中点为T.△B(−1,0),△T(12m-,32),△直线y=−2x+4平分平行四边形ABCD的面积,△直线y=−2x+4经过点T,△32=−2×12m-+4,△m=72,△D(72,3),故答案为:(72,3).【点睛】本题考查中心对称,平行四边形的性质,一次函数的性质等知识,解题关键是理解题意,灵活运用所学知识解决问题.9.A【分析】根据三角形中线的性质可得S△EBC=12S△ABC,1124BEF BEC ABCS S S==,结合已知条件即可求解.【详解】解:△点D ,E 分别为边BC , AD 中点, 111,,222ABD ABC BED ABD CED ABD SS S S S S ∴===, 12BED DEC BEC ABC S S S S ∴+==,△F 是EC 的中点, 12BEF BEC S S =, 14BEF ABCS S ∴=, △ABC 的面积等于4cm 2,△S △BEF =1cm 2,即阴影部分的面积为1cm 2,故选:A .【点睛】本题主要考查了三角形的中线的性质,掌握三角形的中线的性质是解题的关键.10.C【分析】根据三角形任意两边的和大于第三边,进而得出答案.【详解】解:三角形三边长分别为2,8,x ,8282x ∴-<<+,即:610x <<,只有9符合,故选:C .【点睛】此题主要考查了三角形三边关系,解题的关键是正确把握三角形三边关系定理.11.C【详解】分析:由已知条件可知,顺次连接A 、B 、C 三点可得△ABC ,在分别以AB 、BC 和AC 为对角线各作出一个以点A 、B 、C 为顶点的平行四边形,如下图,由此即可得到本题答案了.详解:△点A 、B 、C 不在同一条直线上时,△顺次连接A 、B 、C 三点可得△ABC ,△分别以AB 、BC 和AC 为对角线各作出一个以点A 、B 、C 为顶点的平行四边形,如下图所示:△当A 、B 、C 三点不在同一条直线上,则以这三点为顶点的平行四边形共有3个.故选C.点睛:知道以三角形的每一条边为一条对角线都可以画出一个以该三角形的三个顶点为顶点的平行四边形,是解答本题的关键.12.A【分析】仔细观察图形变化,找到图形变化的规律,利用规律求解.【详解】解:第1个图里有6个点,6=4+2;第2个图有8个点,8=4+2×2;第3个有10个点,10=4+3×2;…则第n 个图中点的个数为4+2n ,令4+2n =2022, 解得n =1009.故选:A .【点睛】本题主要考查图形的变化规律,解题的关键是根据图形得出每往后一个图形,点的个数相应增加2个.13.(1)75DPC ∠=︒(2)30APN ∠=︒或150︒(3)2180α-︒【分析】(1)先算出9045DPB BDP ∠=︒-∠=︒,9060CPA ACP ∠=︒-∠=︒,然后根据平角的定义,求出75DPC ∠=︒即可;(2)分点C 在MN 上方和点C 在MN 下方两种情况进行讨论,根据平行线的性质,求出结果即可;(3)延长PB 截取BG =PB ,在MN 上截取AH =AP ,连接GH ,交BD 于点E ,交AC 于点F ,连接PE 、PF ,此时△PEF 的周长最小,根据三角形外角的性质和垂直平分线的性质,求出EPF ∠的度数即可.(1)解:△90DBP CAP ∠=∠=︒,45BDP ∠=︒,30ACP ∠=︒,△9045DPB BDP ∠=︒-∠=︒,9060CPA ACP ∠=︒-∠=︒,△PA ,PB 与直线MN 重合,△18075DPC DPB CPA ∠=︒-∠-∠=︒.(2)当点C 在MN 上方时,如图所示:PC BD ∥,45BDP ∠=︒,△45CDP BDP ∠=∠=︒,△45DPB ∠=︒,60CPA ∠=︒,△18030APN BPD CPD CPA ∠=︒-∠-∠-∠=︒;当点C 在MN 下方时,如图所示:△PC BD ∥,90DBP ∠=︒,△90BPC DBP ∠=∠=︒,18090CPN BPC ∴∠=︒-∠=︒,△6090150APN APC CPN ∠=∠+∠=︒+︒=︒;综上分析可知,30APN ∠=︒或150︒.(3)延长PB 截取BG =PB ,在MN 上截取AH =AP ,连接GH ,交BD 于点E ,交AC 于点F ,连接PE 、PF ,此时△PEF 的周长最小,如图所示:△90DBP CAP ∠=∠=︒,△DB GP ⊥,CA PH ⊥,△DB 垂直平分PG ,CA 垂直平分PH ,△EG =EP ,FP =FH ,△EGP EPG ∠=∠,PHF HPF ∠=∠,△△MPG 是△PGH 的外角,△MPG EGP PHF EPG FPH ∠=∠+∠=∠+∠,180MPG α∠=︒-,△180EPG FPH MPG α∠+∠=∠=︒-,△()EPF APB EPG FPH ∠=∠-∠+∠()180αα=-︒-2180α=-︒【点睛】本题主要考查了平行线的性质,垂直平分线的性质,等腰三角形的性质,直角三角形两锐角互余,根据题意作出图形,并进行分类讨论,是解题的关键.14.(1)证明见详解(2)证明见详解【分析】(1)△证明ADG AEG ≌△即可;△连接BG ,CG ,证明ADG BCG ≌△,BOE GOC ∽△△即可证明;(2)△的结论和(1)中证明一样,证明ADG AEG ≌△即可;△的结论,作DM BC GM ⊥,连接,证明BOE GOM ∽△△即可.(1)证明:△证明过程:四边形ABCD 为矩形,90ABC BAD ∴∠=∠=︒AF 平分BAD ∠45BAF DAF ∴∠=∠=︒ABF ∴为等腰直角三角形AB BF ∴=BE FC =AB BE BF CF AE BC AD ∴+=+==,即AG AG =∴ADG AEG ≌△∴GE GD =△证明:连接BG ,CG ,G 为AF 的中点,四边形ABCD 为矩形,90ABC BAD AD BC ∴∠=∠=︒=,BG AG FG ∴==AF 平分BAD ABF ∠,为等腰直角三角形,45BAF DAF ABG CBG ∴∠=∠=︒=∠=∠∴ADG BCG ≌△∴ADG BCG ∠=∠ADG AEG ≌△E ADG ∴∠=∠E BCG ∴∠=∠BOE GOC ∠=∠BOE GOC ∴∽△△BO GO GO BOBE GC GD CF ∴===∴BO GD GO FC ⋅=⋅(2)作DM BC BC M GM GN DM DM N ⊥⊥交于,连接,作交于点,如图所示90DMB GNM GND DMC ∴∠=︒=∠=∠=∠由(1)同理可证:ADG AEG ≌△E ADG ∴∠=∠四边形ABCD 为平行四边形AD BC ∴∥90ADM DMC ∴∠=∠=︒BC GN AD ∴∥∥G 为AF 的中点,由平行线分线段成比例可得DN MN =DG MG ∴=,,GDM GMDADG BMG EBOE GOM ∠=∠BOE GOM ∴∽△△BO GO GO BO BE GM GD CF∴=== ∴BO GD GO FC ⋅=⋅【点睛】本题考查了以矩形与平行四边形为桥梁,涉及全等三角形的证明,相似三角形的证明,正确作出辅助线并由此得到相应的全等三角形和相似三角形是解题的关键.15.(1)3对;,,AED DFA AEC DFB AFB DEC ≌≌≌;(2)AED DFA ≌,证明见解析.【分析】根据已知条件,结合三角形全等的判定定理,推理即可得到正确答案.【详解】解:(1)3对;,,AED DFA AEC DFB AFB DEC ≌≌≌;(2)我会说明AED DFA ≌.证明:在AED 和DFA 中,△,,,DE AF DA AD AE DF =⎧⎪=⎨⎪=⎩△()AED DFA SSS ≌.【点睛】本题考查三角形全等的判定定理,根据定理内容找到全等条件是解题关键.。
(完整版)平行四边形的性质习题(有答案)

平行四边形的性质测试题一、选择题(每题 3 分共 30 分)1.下边的性质中,平行四边形不必定具备的是()A.对角互补B.邻角互补C.对角相等D.内角和为 360°2.在中,∠ A:∠ B:∠ C:∠ D 的值能够是()A .1:2:3:4B .1:2:1:2C .1:1:2:2 D.1: 2:2:13.平行四边形的对角线和它的边能够构成全等三角形()A.3对B.4 对 C .5对D. 6 对A D 4.以下图,在中,对角线 AC、BD交于点 O,?以下式子中一O 定建立的是()B CA.AC⊥ BD B . OA=OC C. AC=BD D .AO=OD5.以下图,在中, AD=5,AB=3,AE均分∠ BAD交BC A D边于点 E,则线段 BE、 EC的长度分别为()BE C A .2和3 B.3和2 C .4和1 D .1和46.的两条对角线订交于点 O,已知 AB=8cm,BC=6cm,△AOB的周长是 18cm,那么△ AOD的周长是()A .14cmB .15cmC .16cmD .17cm7.平行四边形的一边等于14,它的对角线可能的取值是()A .8cm和 16cmB .10cm和 16cmC . 12cm和 16cmD . 20cm和 22cm 8.如图,在中,以下各式不必定正确的选项是()A.∠ 1+∠ 2=180° B .∠ 2+∠ 3=180C.∠ 3+∠ 4=180°D.∠ 2+∠4=180°9.如图,在中,∠ ACD=70°,AE⊥ BD于点E,则∠ ABE等于()A、20°B、25° C 、 30° D 、35°10.如图,在△ MBN中, BM=6,点 A、C、D 分别在 MB、NB、MN上,四边形 ABCD为平行四边形,∠NDC=∠ MDA,那么的周长是()二、填空题(每题 3 分共 18 分)11.在中,∠ A:∠ B=4:5,则∠ C=______.12.在中, AB:BC=1:2,周长为 18cm,则 AB=______cm,AD=_______cm.13.在中,∠A=30°,则∠ B=______,∠C=______,∠D=________.14.如图,已知:点 O是的对角线的交点, ?AC=?48mm,?BD=18mm,AD=16mm,那么△ OBC的周长等于 _______mm.15.如图,在中,E、F是对角线BD上两点,要使△ ADF≌△ CBE,还需增添一个条件是 ________.16.如图,在中,EF∥ AD,MN∥ AB,那么图中共有_______?个平行四边形.三、解答题17.已知:如图,在中,E、F是对角线AC?上的两点,AE=CF.BE与DF的大小有什么关系,并说明原因。
平行四边形性质练习题(打印) 2
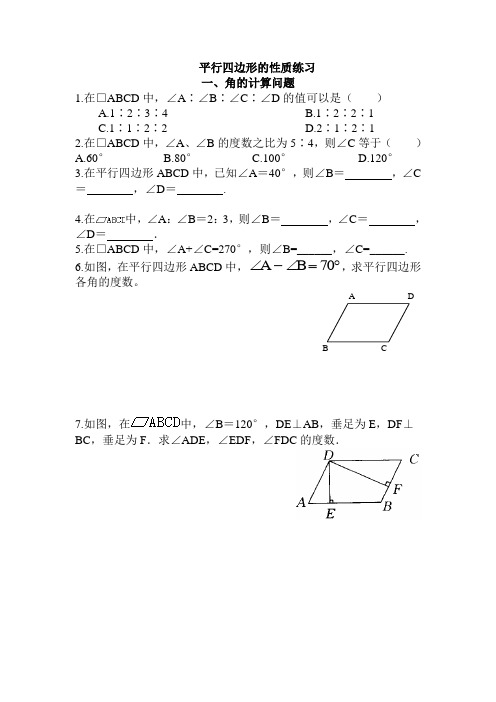
平行四边形的性质练习一、角的计算问题1.在□ABCD 中,∠A ∶∠B ∶∠C ∶∠D 的值可以是( )A.1∶2∶3∶4B.1∶2∶2∶1C.1∶1∶2∶2D.2∶1∶2∶12.在□ABCD 中,∠A 、∠B 的度数之比为5∶4,则∠C 等于( ) A.60° B.80° C.100° D.120°3.在平行四边形ABCD 中,已知∠A =40°,则∠B = ,∠C = ,∠D = .4.在中,∠A :∠B =2:3,则∠B = ,∠C = ,∠D = .5.在□ABCD 中,∠A+∠C=270°,则∠B=______,∠C=______.6.如图,在平行四边形ABCD 中,∠-∠=︒A B 70,求平行四边形各角的度数。
A DB C7.如图,在中,∠B =120°,DE ⊥AB ,垂足为E ,DF ⊥BC ,垂足为F .求∠ADE ,∠EDF ,∠FDC 的度数.二、边长计算问题1.□ABCD 的周长为36 cm ,AB=75BC ,则较长边的长为( )A.15 cmB.7.5 cmC.21 cmD.10.5 cm 2.如图,□ABCD 中,EF 过对角线的交点O ,AB=4,AD=3,OF=1.3,则四边形BCEF 的周长为( )A.8.3B.9.6C.12.6D.13.6 3.在□ABCD 中,AB=3,BC=4,则□ABCD 的周长等于_______. 4.在平行四边形ABCD 中,已知AB =8,周长等于24,则BC = ,CD = ,AD = . 5.已知的周长为28cm ,AB :BC =3:4,则AB = ,BC = ,CD = ,AD = .6.在中,∠A =30°,AB =7 cm ,AD =6 cm ,则=____________.7.平行四边形两邻边分别是4和6,其中一边上的高是3,则平行四边形的面积是____________8.平行四边形邻边长是4 cm 和8cm ,一边上的高是5 cm ,则另一边上的高是____________.三、对角线问题1.平行四边行的两条对角线把它分成全等三角形的对数是()A.2B.4C.6D.82.中,周长为20cm,对角线AC交BD于点O,△OAB比△OBC的周长多4,则边AB=____________,BC=____________.3.如图,中,对角线AC长为10 cm,∠CAB=30°,AB长为6 cm,则的面积是____________.4.如图,在平行四边形ABCD中,已知对角线AC和BD相交于点O,ΔAOB的周长为15,AB=6,那么对角线AC和BD的和是多少?5.如图,已知的周长为60 cm,对角线AC、BD相交于点O,△AOB的周长比△BOC的周长长8cm,求这个四边形各边长.6.如图,如果△AOB与△AOD的周长之差为8,而AB∶AD=3∶2,那么的周长为多少?1.如图,在□ABCD中,AB=AC,若□ABCD的周长为38 cm,△ABC 的周长比□ABCD的周长少10 cm,求□ABCD的一组邻边的长.2.如图,在□ABCD中,对角线AC,BD相交于点O,MN是过O点的直线,交BC于M,交AD于N,BM=2,AN=2.8,求BC和AD的长.3.如图,在□ABCD中,E、F分别是BC、AD上的点,且AE∥CF,AE与CF相等吗?说明理由.4.如图,在□ABCD中,O是对角线AC、BD的交点,BE⊥AC,DF ⊥AC,垂足分别为E、F.那么OE与OF是否相等?为什么?。
平行四边形的性质作业

平行四边形的性质1.__________________________________的四边形叫做平行四边形。
;平行四边形对边___________,对角____________平行四边形的对角线。
2.如图,四边形ABCD是平行四边形,AB=6cm,BC=8cm,∠B=70°,则AD=________,CD=______,∠D=__________,∠A=_________,∠C=__________.平行四边形的周长为:_________________3.如图,四边形ABCD是平行四边形,对角线AC、BD相交于点O,边AB可以看成由_____________平移得来的,△ABC可以看成由__________绕点O旋转______________得来。
4、平行四边形ABCD中∠A=50°,AB=a,BC=b.则:∠B=____ ,∠C= ____ ,平行四边形ABCD的周长= _______ .5、.如图:平行四边形ABCD中∠A+∠C=200°.则:∠A= _______,∠B= _________ .6、如图(1),在平行四边形ABCD中,AC、BD交于点O,则图中相等的角有()对. (A)8 (B)6 (C)4 (D)27、.如图:平行四边形ABCD的周长为36,AB=8,BC=________8、平行四边形ABCD的周长为50cm,两邻边之差为5cm, AB=_______,BC=________. AD=________,CD=______,9、在ABCD中,已知AB:BC=3:5,且周长等于48,则AB=_______,BC=________. AD=________,CD=______,10、在ABCD中,若∠A-∠B=70°,求∠D=______,∠A=______,∠C=______.∠B=_______的度数。
11、平行四边形ABCD中,∠A︰∠B︰∠C︰∠D可以是()A、1︰2︰2︰1B、2︰1︰1︰2C、2︰2︰1︰1D、2︰1︰2︰112、平行四边形ABCD的周长是10㎝,⊿ABC的周长是8㎝,则对角线AC的长是()A、2㎝B、3㎝C、4㎝D、5㎝13、.平行四边形ABCD中,AE平分∠DAB, ∠DAE=20°,则∠C=_________,∠B_________.14、在平行四边形ABCD中,对角线AC与BD相交于点O,已知AB=3,BC=4,AC =6,BD=5,那么AO=()厘米,OD=()厘米。
平行四边形性质练习题

平行四边形性质练习题平行四边形性质练习题平行四边形是初中数学中一个重要的几何概念,它具有一些独特的性质和特点。
在本文中,我们将通过一些练习题来加深对平行四边形性质的理解和应用。
练习题1:已知ABCD是一个平行四边形,AC的延长线与BD的延长线交于点E,证明AE与BC平行。
解析:我们可以通过证明三角形ABE与三角形CDE相似来证明AE与BC平行。
首先,由于ABCD是一个平行四边形,所以AB与CD平行,即∠ABE与∠CDE是对应角,且∠AEB与∠CED是共顶角,因此∠ABE≌∠CDE。
又因为∠AEB与∠CED互为对应角,所以∠AEB≌∠CED。
根据相似三角形的性质,我们可以得出三角形ABE与三角形CDE相似。
因此,我们可以得出AE与BC平行的结论。
练习题2:已知ABCD是一个平行四边形,E是AD的中点,F是BC的中点,连接EF并延长交于点G,证明AG与BC平行。
解析:我们可以通过证明三角形AGE与三角形BFC相似来证明AG与BC平行。
首先,由于ABCD是一个平行四边形,所以AB与CD平行,即∠AGE与∠BFC是对应角,且∠AEG与∠BFC是共顶角,因此∠AGE≌∠BFC。
又因为∠AEG与∠BFC互为对应角,所以∠AEG≌∠BFC。
根据相似三角形的性质,我们可以得出三角形AGE与三角形BFC相似。
因此,我们可以得出AG与BC平行的结论。
练习题3:已知ABCD是一个平行四边形,E是AD的中点,F是BC的中点,连接EF并延长交于点G,证明AG=2GF。
解析:根据题意,我们可以得出AE=ED,BF=FC。
由于E是AD的中点,所以AE=ED=1/2AD;同理,由于F是BC的中点,所以BF=FC=1/2BC。
根据平行四边形的性质,我们可以得出AD=BC。
因此,AE=1/2AD=1/2BC=BF。
根据三角形的等边性质,我们可以得出三角形AGE与三角形BFC是等边三角形。
因此,AG=AE+EG=BF+FC=2BF=2GF。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
10月15日平行四边形的性质1
预习评估
1. __________________________________的四边形叫做平行四边形。
__________________________叫做平行四边形的对角线
平行四边形的对角线把它分成的两个三角形______________.
2. 平行四边形对边___________,对角____________
3. 如图,四边形ABCD 是平行四边形,AB=6cm,BC=8cm ,∠B=70°,则
AD=________,CD=______,∠D=__________,∠
A=_________,∠C=__________.
4. 如图,四边形ABCD 是平行四边形,对角线AC 、BD 相交于点O ,边AB 可以看成由_____________
平移得来的,△ABC 可以看成由__________绕点O 旋转______________得来。
例题与练习
例题1、平行四边形得周长为50cm ,两邻边之差为5cm,求各边长。
变题1.平行四边形ABCD 的周长为40cm,两邻边AB 、AC 之比为2:3,则AB=_______,BC=________.
变题2.四边形ABCD 是平行四边形,∠BAC=90°,AB=3,AC=4,求AD 的长。
例题2.平行四边形ABCD 中,∠A-∠B=20°,求平行四边形各内角的度数。
变题3.平行四边形ABCD 中,AE 平分∠DAB, ∠DEA=20°,则∠C=_________,∠B_________.
变题4.如图,在平行四边形ABCD 中,∠BAC=34°, ∠ACB=26°,求∠DAC 与∠D 的度数。
例题3.如图,在平行四边形ABCD 中,CE ⊥AD,CF ⊥BA 交BA 的延长线于F ,∠FBC=30°,CE=3cm,CF=5cm,求平行四边形ABCD 的周长。
变题5.如图,平行四边形ABCD 的周长为50,其中AB=15,
∠ABC=60°,求平行四边形面积。
A
B
C D A B
C D O A B C D E A B C D
F E A B C D
A B C D。
