第3-4章平稳时间序列分析-模型检验.
合集下载
第四章平稳时间序列模型的建立
将上式展开得：
xt 1xt1 p xtp 0 at 1at1 2at2 qatq
此时，所要估计的未知参数有p+q+1个.
第二节 模型识别与定阶
一、模型识别 二、模型定阶
一、模型识别
• 基本原则
ˆk
拖尾 q阶截尾
拖尾
ˆkk
P阶截尾 拖尾
拖尾
选择模型 AR(P) MA(q)
ARMA(p,q)
• 序列的非平稳包括均值非平稳和方差非 平稳.
• 均值非平稳序列平稳化的方法：差分变 换.
• 方差非平稳序列平稳化的方法：对数变 换、平方根变换等.
• 序列平稳性的检验方法和手段主要有： 序列趋势图、自相关图、单位根检验、 非参数检验方法等等.
一、平稳性检验—图检验方法
（一）时序图检验
–根据平稳时间序列均值、方差为常数的性 质，平稳序列的时序图应该显示出该序列 始终在一个常数值附近随机波动，而且波 动的范围有界、无明显趋势及周期特征.
–检验1949年——1998年北京市每年最高气温 序列的平稳性
例1 时序图
例1 自相关图
例2 时序图
例2 自相关图
例3 时序图
例3 自相关图
二、纯随机性检验
（一）纯随机序列的定义
• 纯随机序列也称为白噪声序列，它 满足如下两条性质
(1)EX t , t T
(2)
(t,
s)
2,t
s
,
例5、对1950年—1998年北京市城乡居民定期储
蓄所占比例序列的平稳性与纯随机性进行检验
自相关图
白噪声检验结果
延迟阶数 6 12
LB统计量检验
LB检验统计 量的值
75.46
xt 1xt1 p xtp 0 at 1at1 2at2 qatq
此时，所要估计的未知参数有p+q+1个.
第二节 模型识别与定阶
一、模型识别 二、模型定阶
一、模型识别
• 基本原则
ˆk
拖尾 q阶截尾
拖尾
ˆkk
P阶截尾 拖尾
拖尾
选择模型 AR(P) MA(q)
ARMA(p,q)
• 序列的非平稳包括均值非平稳和方差非 平稳.
• 均值非平稳序列平稳化的方法：差分变 换.
• 方差非平稳序列平稳化的方法：对数变 换、平方根变换等.
• 序列平稳性的检验方法和手段主要有： 序列趋势图、自相关图、单位根检验、 非参数检验方法等等.
一、平稳性检验—图检验方法
（一）时序图检验
–根据平稳时间序列均值、方差为常数的性 质，平稳序列的时序图应该显示出该序列 始终在一个常数值附近随机波动，而且波 动的范围有界、无明显趋势及周期特征.
–检验1949年——1998年北京市每年最高气温 序列的平稳性
例1 时序图
例1 自相关图
例2 时序图
例2 自相关图
例3 时序图
例3 自相关图
二、纯随机性检验
（一）纯随机序列的定义
• 纯随机序列也称为白噪声序列，它 满足如下两条性质
(1)EX t , t T
(2)
(t,
s)
2,t
s
,
例5、对1950年—1998年北京市城乡居民定期储
蓄所占比例序列的平稳性与纯随机性进行检验
自相关图
白噪声检验结果
延迟阶数 6 12
LB统计量检验
LB检验统计 量的值
75.46
第3-4章平稳时间序列分析-模型检验.
例3.13续：用AIC准则和SBC准则评判例3.13中 两个拟合模型的相对优劣。
模型 MA(2) AR(1) AIC 7.49 7.43 SBC 7.59 7.50
结果： AR(1)优于MA(2)
六、序列预测
所谓预测是要利用序列已观测到的样本值对 序列未来某个时刻的取值进行估计。预测方法主 要有线性最小方差预测和条件期望预测。
i 0 i 0
l 1
2 Gi2
i 0
l 1
当 Gl i Wi , i 0,1, 2,
此时
时，预测方差达到最小，
xt l
的预测值为：
ˆt (l ) W0t W1t 1 x
（2）条件期望预测
xt l t l G1 t l 1 et (l )
ˆ ˆ
t 1 n t 1
nk
t t k
2 ˆ t
例2.5续：检验1950年——1998年北京市城乡居民 定期储蓄比例序列拟合模型的显著性。 残差白噪声序列检验结果： 延迟阶数 6 LB统计量 5.83 P值 0.3229 检验结论
12
18
10.28
11.38
0.5050
0.8361
2 ˆ ˆ t ------残差平和 2 n
T ------待估参数的个数
中心化的ARMA(p,q)模型， T p q 1 非中心化的ARMA(p,q)模型， T pq2
t 1
理论上， AIC和 SBC的值越小越好（注意： 两者皆可为负）。当模型的拟合优度上升时， AIC和 SBC的值会趋于 －∞ 。需注意的是：在 比较两个备选模型的AIC（或 SBC）时，必须基 于相同样本期估计的模型。 SBC具有更优的大样本特性，可以证明， SBC准则是最优模型的真实阶数的相合估计 （一致估计）。而在小样本下AIC效用优于 SBC。一般来说， AIC倾向于选择过多参数的 模型，而SBC倾向于选择更为简练模型。 在使用AIC（或 SBC）准则选择模型时， 我们只能得到相对最优模型，而不可能得到绝 对最优模型。（因为不可能比较所有模型的 AIC值 ）。
时间序列分析第三章平稳时间序列分析
注：图中，S号代表序列的观察值；连续曲线代表拟合序列曲线；虚线代表拟合序列的95%上下置信限。
所谓预测就是要利用序列以观察到的样本值对序列在未来某个时刻的取值进行估计。
目前对平稳序列最常用的预测方法是线性最小方差预测。
线性是指预测值为观察值序列的线性函数，最小方差是指预测方差达到最小。
在预测图上可以看到，数据围绕一个范围内波动，即说明未来的数值变化时平稳的。
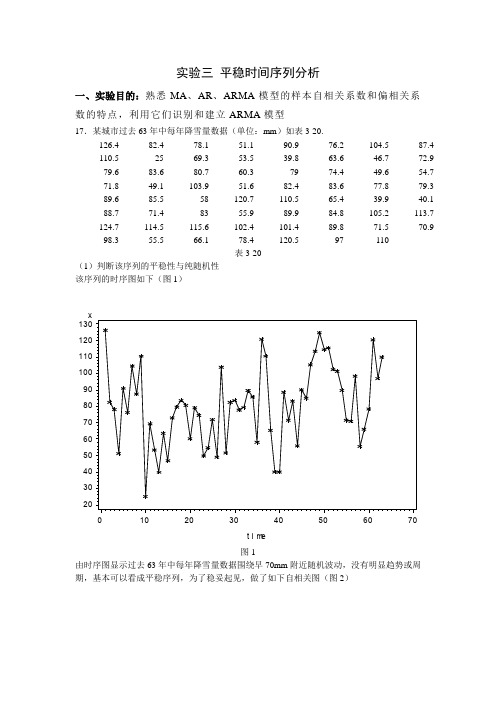
二、课后习题第十七题：根据某城市过去63年中每年降雪量数据（单位：mm）得：（书本P94）程序：data example17_1;input x@@;time=_n_;cards;2579588397 110;proc gplot data=example17_1;plot x*time=1;symbol c=red i=join v=star;run;proc arima data=example17_1;identify var=x nlag=15minic p= (0:5) q=(0:5);run;estimate p=1;run;estimate p=1 noin;run;forecast lead=5id=time out=results;run;proc gplot data=results;plot x*time=1 forecast*time=2 l95*time=3 u95*time=3/overlay;symbol1c=black i=none v=start;symbol2c=red i=join v=none;symbol3c=green i=join v=none l=32;run;（1）判断该序列的平稳性与纯随机性该序列的时序图如下（图a）图a由时序图显示过去63年中每年降雪量数据围绕早70mm附近随机波动，没有明显趋势或周期，基本可以看成平稳序列，为了稳妥起见，做了如下自相关图（图b）图b时序图就是一个平面二维坐标图，通常横轴表示时间，纵轴表示序列取值。
实验三平稳时间序列分析
84.3
82.9
84.7
82.9
81.5
83.4
87.7
81.879.685 Nhomakorabea877.9
89.7
85.4
86.3
80.7
83.8
90.5
84.5
82.4
86.7
83
81.8
89.3
79.3
82.7
88
79.6
87.8
83.6
79.5
83.3
88.4
86.6
84.6
79.7
86
84.2
83
84.8
83.6
82.1
81.4
85
85.8
84.2
83.5
86.5
85
80.4
85.7
86.7
86.7
82.3
86.4
82.5
82
79.5
86.7
80.5
91.7
81.6
83.9
85.6
84.8
78.4
89.9
85
86.2
83
85.4
84.4
84.5
86.2
85.6
83.2
85.7
83.5
80.1
82.2
88.6
图2
自相关图显示该序列自相关系数一直都比较小，1阶开始控制在2倍的标准差范围以内，可以认为该序列自始自终都在零轴附近波动，这是随即性非常强的平稳时间序列。
纯随机性检验见下图：（图3）
图3
6阶以内P值显著小于0.05，可以认为这个拟合模型的残差序列不属于白躁声序列
（2）如果序列平稳且非白躁声，选折适当模型拟合序列的发展
82.9
84.7
82.9
81.5
83.4
87.7
81.879.685 Nhomakorabea877.9
89.7
85.4
86.3
80.7
83.8
90.5
84.5
82.4
86.7
83
81.8
89.3
79.3
82.7
88
79.6
87.8
83.6
79.5
83.3
88.4
86.6
84.6
79.7
86
84.2
83
84.8
83.6
82.1
81.4
85
85.8
84.2
83.5
86.5
85
80.4
85.7
86.7
86.7
82.3
86.4
82.5
82
79.5
86.7
80.5
91.7
81.6
83.9
85.6
84.8
78.4
89.9
85
86.2
83
85.4
84.4
84.5
86.2
85.6
83.2
85.7
83.5
80.1
82.2
88.6
图2
自相关图显示该序列自相关系数一直都比较小，1阶开始控制在2倍的标准差范围以内，可以认为该序列自始自终都在零轴附近波动，这是随即性非常强的平稳时间序列。
纯随机性检验见下图：（图3）
图3
6阶以内P值显著小于0.05，可以认为这个拟合模型的残差序列不属于白躁声序列
（2）如果序列平稳且非白躁声，选折适当模型拟合序列的发展
第4章平稳时间序列预测
今年第一季度该超市月销售额分别为：
101，96，97.2万元 请确定该超市第二季度每月销售额的预测值.
解: 预测值计算
X t 10 0.6 X t 1 0.3 X t 2 t , t ~ N (0,36) x1 101, x2 96, x3 97.2
四月份: 五月份: 六月份:
方法
第四章 平稳时间序列预测
预测
平稳时间序列预测的定义 利用平稳时间序列{Xt ,t=0,±1,±2,…}在时刻t及以 前时刻 t-1,t-2,…的所有信息，对 Xt+l(l>0)进行估计， 相应的预测量记为
ˆ l ， 称为预测步长，t称为预 X t l
测的原点.
第四章 平稳时间序列预测
ห้องสมุดไป่ตู้
第一节 正交投影预测
统计人数 预测人数
ˆ 2002 104 110 6 2002 x2002 x ˆ 2003 108 100 8 2003 x2003 x ˆ 2004 105 109 4 2004 x2004 x
ˆ2004 (1) 100 0.8 2004 0.6 2003 0.2 2002 109.2 x ˆ2004 (2) 100 0.6 2004 0.2 2003 96 x ˆ2004 (3) 100 0.2 2004 100.8 x ˆ2004 (4) 100 x ˆ2004 (5) 100 x
与预测图(预测1999-2003)
例2：MA(q)模型的预测
已知某地区每年常驻人口数量近似服从MA(3)模型 （单位：万人）：
X t 100 t 0.8t 1 0.6 t 2 0.2 t 3 , 25
101，96，97.2万元 请确定该超市第二季度每月销售额的预测值.
解: 预测值计算
X t 10 0.6 X t 1 0.3 X t 2 t , t ~ N (0,36) x1 101, x2 96, x3 97.2
四月份: 五月份: 六月份:
方法
第四章 平稳时间序列预测
预测
平稳时间序列预测的定义 利用平稳时间序列{Xt ,t=0,±1,±2,…}在时刻t及以 前时刻 t-1,t-2,…的所有信息，对 Xt+l(l>0)进行估计， 相应的预测量记为
ˆ l ， 称为预测步长，t称为预 X t l
测的原点.
第四章 平稳时间序列预测
ห้องสมุดไป่ตู้
第一节 正交投影预测
统计人数 预测人数
ˆ 2002 104 110 6 2002 x2002 x ˆ 2003 108 100 8 2003 x2003 x ˆ 2004 105 109 4 2004 x2004 x
ˆ2004 (1) 100 0.8 2004 0.6 2003 0.2 2002 109.2 x ˆ2004 (2) 100 0.6 2004 0.2 2003 96 x ˆ2004 (3) 100 0.2 2004 100.8 x ˆ2004 (4) 100 x ˆ2004 (5) 100 x
与预测图(预测1999-2003)
例2：MA(q)模型的预测
已知某地区每年常驻人口数量近似服从MA(3)模型 （单位：万人）：
X t 100 t 0.8t 1 0.6 t 2 0.2 t 3 , 25
平稳时间序列分析
0
varX t
(1
2 1
2 q
)
2
1
cov( X t , X t1 )
(1
1 2
2 3
q
1
q
)
2
q 1
cov( X t ,
X t q1 )
( q1
1
q
)
2
q
cov( X t , X tq )
q
2
当滞后期不小于q时，Xt旳自协方差系数为0。
所以:有限阶移动平均模型总是平稳旳。
3、ARMA(p,q)模型旳平稳性
• 有时，虽然能估计出一种较为满意旳因果关系回归方程， 但因为对某些解释变量将来值旳预测本身就非常困难，甚 至比预测被解释变量旳将来值更困难，这时因果关系旳回 归模型及其预测技术就不合用了。
在这些情况下，我们采用另一条预测途径：经过时间 序列旳历史数据，得出有关其过去行为旳有关结论，进而 对时间序列将来行为进行推断。
0
2 X
2
12
在稳定条件下，该方差是一非负旳常数，从而有 ||<1。
而AR(1)旳特征方程
(z) 1 z 0
旳根为
z=1/
AR(1)稳定，即 || <1，意味着特征根不小于1。
例 AR(2)模型旳平稳性。 对AR(2)模型
X t 1 X t1 2 X t2 t
方程两边同乘以Xt，再取期望得：
所使用旳工具主要是时间序列旳自有关函数 （autocorrelation function，ACF）及偏自有关函 数（partial autocorrelation function， PACF ）。
1、AR(p)过程
(1)自有关函数ACF 1阶自回归模型AR(1)
chap 3 平稳时间序列分析
32
方差
平稳AR模型的传递形式
xt G j t j
j 0
两边求方差得
2 Var( xt ) G 2 j , G j为Green函数 j 0
33
例3.2:求平稳AR(1)模型的方差
平稳AR(1)模型的传递形式为
t i xt (1B)i t 1 t i 1 1B i 0 i 0
12
AR(P)序列中心化变换
称 { yt }为 {xt } 的中心化序列 ，令
0
1 1 p
yt xt
13
自回归系数多项式
引进延迟算子，中心化 AR( p) 模型又可 以简记为
( B) xt t
自回归系数多项式(特征多项式)
(B) 1 1 B 2 B p B
zt r t (c1eit c2eit ) c3t3 c ptp
16
非齐次线性差分方程的解
非齐次线性差分方程的特解
使得非齐次线性差分方程成立的任意一个解zt
zt a1 zt1 a2 zt2 a p zt p h(t )
11
AR(p)
具有如下结构的模型称为 p 阶自回归模 型，简记为 AR( p) xt 0 1 xt 1 2 xt 2 p xt p t
p 0 2 E ( t ) 0，Var( t ) , E ( t s ) 0, s t Ex 0, s t s t 特别当 0 0 时，称为中心化 AR( p) 模型
37
自相关系数
第三章平稳时间序列分析
欢迎共阅t P p t tt t t x B x x B x Bx x ===---221第3章 平稳时间序列分析一个序列经过预处理被识别为平稳非白噪声序列，那就说明该序列是一个蕴含着相关信息的平稳序列。
3.1 方法性工具 3.1.1 差分运算 一、p 阶差分记t x ∇为t x 的1阶差分：1--=∇t t t x x x记t x 2∇为t x 的2阶差分：21122---+-=∇-∇=∇t t t t t t x x x x x x 以此类推：记t p x ∇为t x 的p 阶差分：111---∇-∇=∇t p t p t p x x x 二、k 步差分记t k x ∇为t x 的k 步差分：k t t t k x x x --=∇3.1.2 延迟算子 一、定义延迟算子相当与一个时间指针，当前序列值乘以一个延迟算子，就相当于把当前序列值的时间向过去拨了一个时刻。
记B 为延迟算子，有延迟算子的性质：1.10=B2.若c 为任一常数，有1)()(-⋅=⋅=⋅t t t x c x B c x c B3.对任意俩个序列{t x }和{t y }，有11)(--±=±t t t t y x y x B4.n t t n x x B -=5.)!(!!,)1()1(0i n i n C B C B in i i nni i n-=-=-∑=其中二、用延迟算子表示差分运算 1、p 阶差分 2、k 步差分3.2 ARMA 模型的性质 3.2.1 AR 模型定义 具有如下结构的模型称为p 阶自回归模型，简记为AR(p):ts Ex t s E Var E x x x x t s t s t t p tp t p t t t ∀=≠===≠+++++=---,0,0)(,)(,0)(,0222110εεεσεεφεφφφφε(3.4)AR(p)模型有三个限制条件：条件一：0≠p φ。
这个限制条件保证了模型的最高阶数为p 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
拟合模型 显著有效
（二）参数的显著性检验
（1）目的： 检验每一个未知参数是否显著非零。删除不显著参 数使模型结构最精简 （2）假设条件：
H0 : j 0 H1 : j 0
（3）检验统计量：
1 j m
T nm
其中
ˆ j j
ˆt2 Q( )
一般地有：
ˆt (l ) 1 x ˆt (l 1) x
x
l 1 t
预测值满足模型差分 方程部分：
ˆt (l ) 1 x ˆt (l 1) 0 x ˆt (0) xt x
AR(2)序列的预测
xt 1xt 1 2 xt 2 t
ˆt (1) E ( xt 1 xt , xt 1 , ) x 1 xt 2 xt 1
例3.13续：用AIC准则和SBC准则评判例3.13中 两个拟合模型的相对优劣。
模型 MA(2) AR(1) AIC 7.49 7.43 SBC 7.59 7.50
结果： AR(1)优于MA(2)
六、序列预测
所谓预测是要利用序列已观测到的样本值对 序列未来某个时刻的取值进行估计。预测方法主 要有线性最小方差预测和条件期望预测。
2 ˆ ˆ t ------残差平方和 2 n
T ------待估参数的个数
中心化的ARMA(p,q)模型， T p q 1 非中心化的ARMA(p,q)模型， T pq2
t 1
理论上， AIC和 SBC的值越小越好（注意： 两者皆可为负）。当模型的拟合优度上升时， AIC和 SBC的值会趋于 －∞ 。需注意的是：在 比较两个备选模型的AIC（或 SBC）时，必须基 于相同样本期估计的模型。 SBC具有更优的大样本特性，可以证明， SBC准则是最优模型的真实阶数的相合估计 （一致估计）。而在小样本下AIC效用优于 SBC。一般来说， AIC倾向于选择过多参数的 模型，而SBC倾向于选择更为简练模型。 在使用AIC（或 SBC）准则选择模型时， 我们只能得到相对最优模型，而不可能得到绝 对最优模型。（因为不可能比较所有模型的 AIC值 ）。
（一）线性预测函数
对于一个平稳可逆的ARMA(p,q)模型来说， 其所有历史未知信息
xt l都可以用已知历史信息
xt , xt 1 ,
表示出来。即
xt l Di xt i
i 0
ˆt (l ) 以 x
D x
i 0
i t i
作为
xt l
的预测值，称
ˆt (l )为 xt 的向前第 l 步线性预测。 x
ˆt (l ) E( xt l xt , xt 1, ) x
对于平稳可逆的ARMA(p,q)模型来说，有
E( xk xt , xt 1, ) xk (k t ) E( k xt , xt 1, ) k (k t )
E( k xt , xt 1, ) 0
E ( xk xt , xt 1 , ) E ( xk t , t 1 , ) xk (k t )
四、模型检验
（一）模型的显著性检验
（1）检验目的 检验模型的有效性（对信息的提取是否充分） （2）检验对象 残差序列 （3）判定原则 一个好的拟合模型应该能够提取观察值序列中几乎 所有的样本相关信息，即残差序列应该为白噪声序列 。 反之，如果残差序列为非白噪声序列，那就意味着残差序 列中还残留着相关信息未被提取，这就说明拟合模型不够 有效。
（4）假设条件 原假设：残差序列为白噪声序列
H0：1 2
m 0, m 1
备择假设：残差序列为非白噪声序列
H1：至少存在某个 k 0, m 1，k m
（5）检验统计量：LB统计量
2 ˆ k 2 LB n(n 2) ( ) ~ (m) ˆk n k k 1 m
i 0 i 0
l 1
2 Gi2
i 0
l 1
当 Gl i Wi , i 0,1, 2,
此时
时，预测方差达到最小，
xt l
的预测值为：
ˆt (l ) W0t W1t 1 x
（2）条件期望预测
xt l t l G1 t l 1 et (l )
xt 1 xt 1 t
ˆt (1) E ( xt 1 xt , xt 1 , ) x E (1 xt t 1 ) xt , xt 1 , 1 xt ˆt (2) E ( xt 2 xt , xt 1 , ) x
E (1 xt 1 t 2 ) xt , xt 1 , 1 E ( xt 1 xt , xt 1 , ) ˆt (1) 1 x 12 xt
6.72
<0.0001
显著
例3.8续: 对OVERSHORTS序列的拟合模型进 行检验。
残差白噪声检验结果：
延迟阶数 6 12 LB统计量 P值 结论
3.15 9.05
0.6772 0.6171
模型显著 有效
参数显著性检验结果：
检验参数 均值 t统计量 －3.75 10.60 P值 <0.0004 <0.0001 结论 显著 显著
由此可见，线性最小方差预测与条件期望
预测是一致的。在正态假定下，有
xt l xt , xt 1,
其中：
ˆt (l ),Var[et (l )]) N (x
ˆt (l ) Glt Gl 1t 1 x et (l ) t l G1t l 1
Gl 1t 1
一般地有，预测值 满足模型差分方程部分：
ˆt (l ) 1x ˆt (l 1) 2 x ˆt (l 2) 0 x
ˆt (2) E ( xt 2 xt , xt 1 , ) x ˆt (1) 2 xt 1 x ˆt (3) E ( xt 3 xt , xt 1 , ) x ˆt (2) 2 x ˆt (1) 1 x
ˆ ˆ
t 1 n t 1
nk
t t k
2 ˆ t
例2.5续：检验1950年——1998年北京市城乡居民 定期储蓄比例序列拟合模型的显著性。 残差白噪声序列检验结果： 延迟阶数 6 LB统计量 5.83 P值 0.3229 检验结论
12
18
10.28
11.38
0.5050
0.8361
（二）预测方差最小原则
预测误差： et (l )
ˆt (l ) xt l x
Varx ˆt ( l ) et (l ) min Var et (l )
由于 x ˆt (l ) 是 xt , xt 1 , 的线性函数，所以
该原理也称为线性预测方差最小原理。
（三）条件 ˆ AIC n ln( ) 2T
AIC 2ln( L) n 2T n 2T 惩罚因子为2 1 n 2 ˆ AIC e n 其中： n ------可用的序列观测值的个数 T ------待估参数的个数
ˆt2------残差平方和 ˆ 2
结论 显著 显著
五、模型优化
问题提出：当一个拟合模型通过了检验，说明 在一定的置信水平下，该模型能有效地拟合观 察值序列的波动，但这种有效模型并不是唯一 的。
优化的目的：选择相对最优模型。
例3.13:拟合某一化学序列(附录1.8)
序列自相关图
序列偏自相关图
拟合模型一 根据自相关系数2阶截尾，拟合MA(2)模型 参数估计：
t 1
n
中心化的ARMA(p,q)模型， T p q 1
非中心化的ARMA(p,q)模型， T pq2
n 1 1 2 l ( , x1 , , xn ) [ ln( ) ln 2 S ( )] 2 2 2
由似然函数可以看出上述三个 统计量会选择相同的模型。
i 0 i 0 j 0 i 0
ˆt (l ) Gi t l i (Gl i Wi ) t i et (l ) xt l x
i 0 i 0
l 1
Var (et (l )) [ Gi2 (Gl i Wi ) 2 ] 2
yieldt 51.17301 (1 0.32286 B 0.31009 B ) t
2
模型检验：模型显著有效；三参数均显著。 拟合模型二 根据偏自相关系数1阶截尾，拟合AR(1)模型
参数估计：
yield t 51.26169
t
1 0.42481 B
模型检验：模型显著有效；两参数均显著。
问题：同一个序列可以构造两个拟合模型，两 个模型都显著有效，那么到底该选择哪个模型 用于统计推断呢？
解决办法：确定适当的比较准则，构造适当的统
计量，确定相对最优。
AIC准则（An Information Criterion）
由日本统计学家赤池弘次（Akaike） 1973年提出，称为最小信息量准则。 如何评价模型对数据的拟合程度？通常 似然函数值越大（或估计的残差平方和越小） 越好。一般地，增加模型中滞后变量的个数 会使估计的残差平方和降低。然而，增加模 型中滞后变量的个数，会使需估计的参数增 多，响应地减少自由度，参数估计的难度越 大，估计的精度越差。甚至，包含了无关紧 要的变量还会降低拟合模型的预测效果。所 以，一个好的拟合模型应该是拟合精度和未 知参数个数的综合最优配置。
预测误差
Glt Gl 1t 1
Gl 1 t 1 Gl t Gl 1 t 1 ˆt (l ) x
预测值
ˆ (l ) E ( xt l xt , xt 1 , ) x Var ( xt l xt , xt 1 , ) Var[et (l )]