本时间序列分析第四章小结
人大版时间序列分析基于R(第2版)习题答案
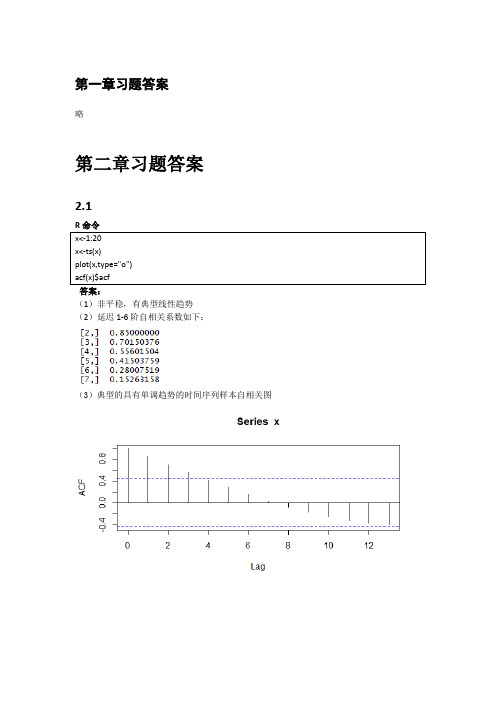
第一章习题答案略第二章习题答案2.1答案:(1)非平稳,有典型线性趋势(2)延迟1-6阶自相关系数如下:(3)典型的具有单调趋势的时间序列样本自相关图2.2(1)非平稳,时序图如下(2)1-24阶自相关系数如下(3)自相关图呈现典型的长期趋势与周期并存的特征2.3R命令答案(1)1-24阶自相关系数(2)平稳序列(3)非白噪声序列Box-Pierce testdata: rainX-squared = 0.2709, df = 3, p-value = 0.9654X-squared = 7.7505, df = 6, p-value = 0.257X-squared = 8.4681, df = 9, p-value = 0.4877X-squared = 19.914, df = 12, p-value = 0.06873X-squared = 21.803, df = 15, p-value = 0.1131X-squared = 29.445, df = 18, p-value = 0.04322.4答案:我们自定义函数,计算该序列各阶延迟的Q统计量及相应P值。
由于延迟1-12阶Q统计量的P值均显著大于0.05,所以该序列为纯随机序列。
2.5答案(1)绘制时序图与自相关图(2)序列时序图显示出典型的周期特征,该序列非平稳(3)该序列为非白噪声序列Box-Pierce testdata: xX-squared = 36.592, df = 3, p-value = 5.612e-08X-squared = 84.84, df = 6, p-value = 3.331e-162.6答案(1)如果是进行平稳性图识别,该序列自相关图呈现一定的趋势序列特征,可以视为非平稳非白噪声序列。
如果通过adf检验进行序列平稳性识别,该序列带漂移项的0阶滞后P值小于0.05,可以视为平稳非白噪声序列Box-Pierce testdata: xX-squared = 47.99, df = 3, p-value = 2.14e-10X-squared = 60.084, df = 6, p-value = 4.327e-11(2)差分序列平稳,非白噪声序列Box-Pierce testdata: yX-squared = 22.412, df = 3, p-value = 5.355e-05X-squared = 27.755, df = 6, p-value = 0.00010452.7答案(1)时序图和自相关图显示该序列有趋势特征,所以图识别为非平稳序列。
时间序列分析——基于R(王燕)第四章

第四章:非平稳序列的确定性分析题目一:()()()()()()()12312123121231ˆ14111ˆˆ2144451.1616T T T T T T T T T T T T T T T T T T T T T xx x x x xx x x x x x x x x x x x x x x -------------=+++⎡⎤=+++=++++++⎢⎥⎣⎦=+++ 题目二:因为采用指数平滑法,所以1,t t x x +满足式子()11t t t x x x αα-=+-,下面式子()()11111t t t t t tx x x x x x αααα-++=+-⎧⎪⎨=+-⎪⎩ 成立,由上式可以推导出()()11111t t t t x x x x αααα++-=+-+-⎡⎤⎣⎦,代入数据得:2=5α. 题目三:()()()21221922212020192001ˆ1210101113=11.251ˆ 1010111311.2=11.04.5ˆˆˆ10.40.6.i i i xxxx x x x x αα-==++++=++++===+-=⋅∑(1)(2)根据程序计算可得:22ˆ11.79277.x= ()222019181716161ˆ2525xx x x x x =++++(3)可以推导出16,0.425a b ==,则425b a -=-. 题目四:因为,1,2,3,t x t t ==,根据指数平滑的关系式,我们可以得到以下公式:()()()()()()()()()()()()()()()221221 11121111 1111311. 2t t t t t tt x t t t x t t αααααααααααααααααααα----=+-------=-+---+--+++2+, ++2+用(1)式减去(2)式得:()()()()()221=11111.t t tt x t αααααααααααα-------------所以我们可以得到下面的等式:()()()()()()122111=11111=.t t t tt x t t αααααααα+-----------------()111lim lim 1.ttt ttxt tααα+→∞→∞----==题目五:1. 运行程序:最下方。
第四章时间序列分析

1.20 0.9833 a1 a2 a2 a0 a1 a0
(2)ai ai1 ai a0 a0 ai1
1.18 a2 a1 a2 1.20 a0 a0 a1
年份 产值(万元) 环比发展速度
% 定基发展速度
%
1996
1997
100(a0) 120(a1)
——
120
(a1/a0)
100
试求该仓库该月的平均库存量
x xf a af
f
f
a 38 5 42 4 39 15 37 6 411 5 4 15 6 1
1206 38.90(台) 31
计算公式 : a af f
x 库存量 a
38 42 39 37 41 合计
f 间隔 f
5 4 15 6 1 31
六 125 100
12(5 )
第四章 时间序列分析
相对数、平均数时间数列序时平均数的计算方法:
1、列出原型公式:c a
3、计算:c a
b
b
2、分别求出a 与b
[例]某车间今年4月份生产工人出勤情况如下,试求该车间4
月份平均工人出勤率。
时间 1—8 9—11 12—20
应出勤数 实际出勤
45
43
第四章时间序列分析
统计实例
对于企业,有关经营管理的各种问题都需要作出预测,然后才能 根据预测结果对生产活动进行决策。而预测的一个重要方法就是对 未来情况进行推测,其原因是企业的生产或经营状况常常随着时间 推移而发生变化。
例如:材料和备用件的库存、产品的销售、工人的工资与产品 的价格水平、生产过程的质量控制,乃至整个企业的变化等,都会 因时间的变化而呈现出动态变化的过程。因此有必要也完全有可能 对现象发展变化的历史资料进行分析,找出现象的发展趋势和变动 规律并据以预测未来。
第四章_时间序列分析

af 计算公式: a f
第四章 时间序列分析
(3)间隔相等、数据不连续资料※
[例]试求 A 厂成品仓库第一季度的平均库存量 月初 一 二 三 四 五 库存量 a 38(a1) 42(a2) 39(a3) 37(a4) 41(a5)
38 42 42 39 39 37 1 1 1 2 2 2 a 111 1 1 (a1 a2 ) (a2 a3 ) (a3 a4 ) a1 a2 a3 an 2 a 2 2 2 2 n 1 3 首尾折半法 1 1 a1 a2 a3 a4 n指标值个数 2 39.5(台) 2 4 1 n1时间长度
第四章 时间序列分析
(二)相对数时间序列 相对数时间序列是指由反映事物之间数量对比关系的相 对数所构成的时间序列。该相对数是两个有关变量的比值。 具体地说,它可以是两个时期数、两个时点数、两个相对数、 两个平均数或者一个时期数与一个时点数对比而成。例如, 表3-2中的第三产业增加值比重就是由第三产业的总增加值与 国内生产总值这两个时期数对比而形成的。 (三)平均数时间序列 平均数时间序列是指由反映事物某一数量特征在不同时 间上的一般水平的平均指标所构成的时间序列。例如,表3-2 中的社会劳动生产率时间序列即为平均数时间序列。
第四章 时间序列分析
2、数量关系
(1)环比发展速度=定基发展速度。(总速度)
a a a a1 a2 a a a n1 n n 1 2 2 1.20 0.9833 1.18 a0 a1 an2 an1 a0 a0 a1 a0
(2)相邻的两个定基发展速度的商等于相应的环比发展速度。 ai ai 1 ai a2 a1 a2 1.18 0.9833 a0 a0 ai 1 a0 a0 a1 1.20
计量地理学 第四章 时间序列分析

第四章时间序列分析每一个时间序列都是事物变化过程中的一个样本,通过对样本的研究、分析,找出过程的特性、最佳的数学模型、估计模型中的参数,检验利用数学模型进行统计预测的精度。
如同描述随机变量一样,利用随机过程的一些数字特征来描述随机时间序列的基本统计特性。
地理要素的空间分布规律是地理系统研究的中心内容。
但是空间与时间是客观事物存在的形式,两者之间是互相联系而不能分割的。
因此,我们常常要分析要素在时间上的变化,在地理系统研究中,就称为地理过程。
据此来阐明地理现象发展的过程和规律。
1.通过对时间序列的研究,阐明对象发展的过程和规律。
现在的现象,往往必须从历史发展中寻找原因和依据。
这和其它学科是共同的。
2.时间上的变化是地理系统的本质特征。
很难找到在时间上不发生变化的地理系统,不同地区的不同变化速率,构成空间变化的主要特征。
3.空间差异有时还可以理解为特定区域地理系统或其要素的时间上变化在区域上的“投影”。
对同一种要素在一定时期的连续观察就确定出现象的时间序列。
许多时间序列的分析都是利用图解法来解决的。
在这种图象中,横轴是时间测度,纵轴是所研究的要素的数值。
第一节时间序列分析基本方法时间序列分析是地理预测的过程,主要研究地理要素及地理活动的时间变化趋势、季节变化、周期变化和不规则变化等规律。
一、图象法时间序列图象有两种表示方法:严格地说,线状图只能用于图象上与变量数值有关的每一点都与时间相对应的情况,例如逐日平均气温图象、人口增长图象等等。
如果变量数值是与各个时段有关,例如:月雨量、年出生率、24小时客流量,这种情况则用柱状图象表示更为合适。
但是,线状图也常用于表示与时段有关的变量。
这是因为线状图容易画、省时间,并且几条线可以叠加在一起,易于比较其趋势。
不过应该注意,不能用与时段有关的线状图进行内插求值。
这是因为一个时段内的每一点,并没有相对应的值。
比如,从年出生率线状图中,不能求出瞬时的或日、月的出生率。
时间序列分析第四章ARMA模型的特性王振龙第二版

一、自协方差函数
• 理论自协方差函数和自相关函数 对于ARMA系统来说,设序列的均值为零,则自协方差函数
k E Xt Xtk
自相关函数
k
k 0
• 样本自相关函数的计算
在拟合模型之前,我们所有的只是序列的一个有限
样本数据,无法求得理论自相关函数,只能求样本的自
= 1.1
-4.0E+10 X
-6.0E+10
25 50 75 100 125 150 175 200 225 250
X
= -1.1
24
20
20
16 15
12
10
8
5
4
0
0
-5
-10 -4
25 50 75 100 125 150-15175 200 225 250
=1
X -20
25 50 75 100 125 150 175 200 225 250
第四章 ARMA模型的特性
4.1 格林函数和平稳性
一、线性常系数差分方程及其解的一般形式 先回忆线性常系数微分方程及其解的结构:
y(t) a0 y(t) u(t)
可转化为 y(t 1) a0 y(t) u(t) 其中 a0 1 a0
将上述方程中的近似号改为等号,实数t改为自然数k,
MA(m)模型的可逆性条件为其特征方程
V m 1V m1 2V m2 ... m 0 的特征根Vk
满足 Vk 1
• ARMA(n,m)系统格林函数与逆函数的关系
在格林函数的表达式中,用 I j 代替 G,j 代替 ,
代替 ,即可得到相对应的逆函数。
第三节 自协方差函数
时间序列分析04-第四章
第四章 经典谱分析
1 /72
4.1 功率谱估计概述
2 / 72
英国的科学家牛顿最早给出了"谱"的概念 1822年,法国工程师傅里叶提出了著名的傅 里叶谐波分析理论. 由于傅里叶系数的计算是一困难的工作,所 以促使人们研制相应的机器,如英国物理学 家Thomson发明了第一个谐波分析仪用来计 算傅里叶系数 Ak,Bk. 利用该机器画出某一港湾一年的潮汐曲线约 需4小时
11 / 72
现代谱估计的内容极其丰富,涉及的学科及 应用领域也相当广泛,目前尚难对现代谱分 析的方法作出准确的分类. 从现代谱分析的方法上,大致分为参数模型 谱估计和非参数模型谱估计. 前者有AR模型,MA模型,ARMA模型, PRONY指数模型等; 后者有最小方差法,多分量的MUSIC方法等.
7 / 72
1930年,著名的控制理论专家Wiener出版了 他的经典著作"Generalized Harmonic Analysis". 在该书中首次精确的定义了一个随机过程的 自相关函数及功率谱密度,并把谱分析建立 在随机过程统计特征的基础上,即功率谱密 度是随机过程二阶统计量自相关函数的傅里 叶变换.这就是Wiener-Khintchine定理. 该定理把功率谱密度定义为频率的连续函数, 而不再是以前离散的谐波频率的函数.
9 / 72
Yule 提出的自回归方程和线性预测有密切的 关系,Khintchine,Slutcky,Wold等人于 1938年给出了线性预测理论的框架,并首次 建立了自回归模型参数与自相关函数关系的 Yule-Walker方程. Bartlett于1948年首次提出了用自回归模型系 数来计算功率谱. 自回归模型和线性预测都用到了1911年提出 的Toeplitz矩阵结构,Levinson根据该矩阵的 特点于1947年提出计算了Yule-Walker方程 的快速计算方法,所有这些工作都为现代谱 估计的发展打下了基础.
第四章_时间序列分析
• 年底
• •
a4
104
•则:该年平均每月的职工人数为:
•(二)对相对指标或平均指标动态数列计算
•由于各个zi 的对比基数 xi 不尽相同,所以不能将各期 zi 简单算术平均。
•基本公式
•a数列的序时平均数
•b数列的序时平均数
•公式表明:相对指标或平均指标动态数列 • 的序时平均数,是由分子、分母两个 • 数列的序时平均数对比得到的。
一般认为,间隔越短,计算结果就越准确。
例如,由一年中各月底数计算的全年平均数,就比只用年初和年末两 项数据计算的结果更准确。
•⑵ 对间隔不等时点数列求 • (加权序时平均法)
•例4-2-5
•时 间
•职工人数(人 )
• 1月 初
• •
1a012
•
3月初
• 9月 初
• •
a2 105
• •
1a038
•日 期
•职工人数(人 )
• 1日—8 日
• a1 • 102
•9日—15日 •a2
•105
• 16日—30 日
• a3 • 108
•则:1号至30号平均每天的职工人数为:
•②由间断时点数列计算序时平均数
•当时点数列中的数据是每隔一段时间 •(如隔一月、一年等)才观测一次的数据时 ,这样的时点数列为间断时点数列。
•所以
•其中: •所以:
•例4-2-7:某企业商品销售额和库存额资料如下:
•项目
时
•间商品销售额(万元
)•月初库存额(万元
)
•四 •月150
• 45
•五 •月200
• 55
• 六 •七 •月240 •月150
时间序列分析-基于R(第四章作业)
时间序列分析第四章作业T1(p133第1题):程序(1):E4_1=read.table("C:\\Users\\DMXTC\\Documents\\E4_1.txt")# install.packages("aTSA")# library(aTSA)# install.packages("forecast")# library(forecast)par(mfrow=c(1,2))r4_1<-as.matrix(E4_1)d4_1<-as.vector(t(r4_1))T4_1<-ts(d4_1)# #绘制时序图#plot(T4_1,type = "o",col="blue",pch=13,main="表4-8时序图")adf.test(T4_1)#install.packages("caret", dependencies = c("Depends", "Suggests"))for (k in 1:2)print(Box.test(T4_1,lag=6*k))acf(T4_1)pacf(T4_1)fit1<-arima(T4_1,order=c(1,0,1))par(mfrow=c(1,1))fore1<-forecast::forecast(fit1,h=5)plot(fore1,lty=2)lines(fore1$fitted,col=4)fore1图形(1):(2)①时序图绘制如上,时序图显示该序列没有明显的趋势或周期特征,说明该序列没有显著的平稳特征。
进行ADF检验,其检验结果显示如下:> adf.test(T4_1)Augmented Dickey-Fuller Testalternative: stationaryType 1: no drift no trendlag ADF p.value[1,] 0 -3.60 0.01[2,] 1 -3.19 0.01[3,] 2 -3.30 0.01[4,] 3 -3.20 0.01Type 2: with drift no trendlag ADF p.value[1,] 0 -3.65 0.0100[2,] 1 -3.23 0.0256[3,] 2 -3.44 0.0165[4,] 3 -3.48 0.0148Type 3: with drift and trendlag ADF p.value[1,] 0 -3.70 0.0340[2,] 1 -3.29 0.0833[3,] 2 -3.64 0.0388[4,] 3 -3.94 0.0193----Note: in fact, p.value = 0.01 means p.value <= 0.01检验结果显示,该序列所有ADF检验统计量的P值均小于显著性水平(α=0.05),所以可以确定该系列为平稳序列;②对平稳序列进行纯随机性检验,其检验结果如下:Box-Pierce testdata: T4_1X-squared = 25.386, df = 6, p-value = 0.0002896Box-Pierce testdata: T4_1X-squared = 31.153, df = 12, p-value = 0.001867结果显示6阶和12阶延迟的LB统计量的P值都小于显著性水平(α=0.05),所以可以判断该系列为平稳非白噪声序列。
时间序列分析报告心得
时间序列分析报告心得一、引言时间序列分析是一门研究按一定时间顺序排列的数据并通过统计方法对其进行建模、预测和分析的方法。
在时间序列分析的过程中,我们运用了各种统计技术,比如平均数、标准差等,通过对历史数据的分析,我们可以预测未来一段时间内的数据变化趋势和规律。
本篇报告主要总结了我对时间序列分析的学习和实践的心得体会。
二、学习过程在学习时间序列分析的过程中,我首先了解了时间序列分析的基本概念和常用的方法。
我了解到,时间序列分析的目标是通过分析时间序列的内在规律,对未来的发展趋势进行预测。
同时,时间序列分析也可以揭示时间序列中的周期性变化、趋势性变化和季节性变化。
我学习了一些时间序列分析的基本概念,比如平稳性、自相关函数、移动平均、自回归等。
在学习过程中,我尝试了不同的学习方法。
首先,我阅读了一些经典的时间序列分析教材和文献,掌握了基本的理论知识。
其次,我通过在线课程和视频教程学习了时间序列分析的实践技巧。
最后,我参与了一些实际项目,应用时间序列分析模型对数据进行预测和分析。
三、实践应用在时间序列分析的实践应用中,我主要应用了Python编程语言和一些常用的时间序列分析工具包,比如pandas和statsmodels。
通过这些工具,我可以对时间序列数据进行读取、处理、分析和可视化。
我首先通过pandas库读取了时间序列数据,并进行了数据的预处理工作。
预处理包括填充缺失值、平滑数据、去除异常点等步骤,这可以使得模型更准确地反映数据的真实情况。
然后,我使用了statsmodels库来构建时间序列分析模型。
statsmodels库提供了丰富的时间序列模型类和函数,比如ARIMA模型、SARIMA模型等。
通过这些模型,我可以对时间序列数据进行建模和预测。
最后,我使用了matplotlib库对分析结果进行可视化。
可视化可以帮助我们更直观地理解数据的规律和趋势,以及模型的预测效果。
四、心得体会通过学习和实践时间序列分析,我深刻体会到了时间序列分析在实际应用中的重要性和价值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
AIC 准则有过分估计自回归阶数的倾向,
可略加改动,得到BIC准则
n ˆ (n) ln N BIC(n) ln N
2 a
选择使上式达到最小的n0做为最佳阶数。 因为一般有:lnN>2,所以由BIC准则确定的阶数不 大于由AIC准则确定的阶数。
28
第四章 平稳时间序列模型的建立
第三节
模型参数估计
1 k 1 1 k 1 0 k 2 1 0 k 2 2 可以得到: 0 k kk k 1 k 2
偏自相关函数p步截尾, 当k>p时,有
ˆ kk ~ N(0, 1 ) N
12
第四章 平稳时间序列模型的建立
(2)截尾、拖尾性的判断
截尾:从某一步q开始与零是否有显著性差别的显著性 检验。若从某一步q开始与零无显著性差别,即为截尾。 观察是否落入2倍标准差范围内,若是,则与零无显著 性差别,即为截尾。 拖尾:在不长时间内收敛,逐渐衰减至零附近。
1. 模型识别既是模型建立中的一个重要步骤也是一个过程 2. 一个具体的时间序列分析问题:
建立时间序列
建模
应用分析
模型识别 参数估计
诊断检验
4
第四章 平稳时间序列模型的建立
二、用自相关函数和偏自相关函数识别
1. B-J方法模型识别的依据
AR(p)模型 MA(q)模型 ARMA模型 ρ k φ kk 拖尾 p步截尾 q步截尾 拖尾 拖尾 拖尾
选择使上式达到最小的n0做为最佳阶数。 一般做法: (1)对观察数据从低阶到高阶拟合AR模型,
(2)计算相应的FPE值,
(3)选择最小的FPE值对应的AR模型为最佳模型。
25
第四章 平稳时间序列模型的建立
4. AIC准则
最小信息准则
2 ˆa AIC(n) ln (n) 2n N
准则函数:
2 ˆa 用ARMA(n,m)拟合序列{Xt},则拟合残差方差
是n、m、μ的函数(假定μ也是待估参数), 记作
2 ˆa (n, m, )
2 ˆa 定义 AIC(n, m, ) ln (n, m, ) 2(n m 1) / N
27
第四章 平稳时间序列模型的建立
5. BIC准则
时间序列分析
第四章 平稳时间序列模型的建立
第四章 平稳时间序列模型的建立
第四章 平稳时间序列模型的建立
共分六节:
※第一节 ※第二节 ※第三节 ※第四节 ※第五节 ※第六节 模型识别 模型定阶 模型参数估计 模型的适应性检验 建模的其它方法 实例
3
第一节
模型识别
第四章 平稳时间序列模型的建立
一、对模型识别问题的认识 :
6
第四章 平稳时间序列模型的建立
三、实际操作中的问题 1. 零均值的显著性检验 判断时间序列是否是零均值的,即判断给出的 样本序列是否与零有显著性差异(是否显著为零或 显著非零)。
7
第四章 平稳时间序列模型的建立
进行零均值化 若显著非零 不进行零均值化
判断平稳性、 识别、估计、 检验等
这时是将均值作为一个未知 参数代入模型中,模型的形 式也将会有所改变,参数估 计时,需估计序列的均值。
0
[1 2 (1 k ) k ] N N k 1
N 1
在大样本情况下,上面的方差表达式可以近似表示为:
var(X )
0
N
(1 2 k )
k 1
9
第四章 平稳时间序列模型的建立
(2)零均值的显著性判断: 我们考察均值μ的估计 X 的均值和方差,为我们 判断序列是否零均值提供了一种依据。 如果样本均值在以下范围内可认为是零均值过程。
0 2 Var X
另外,由
0 var(X ) (1 2 k ) N k 1
可看出:
若原时间序列是独立随机变量序列,则有 var(X ) N 若Xt之间存在自相关,X 的方差就发生了变化
0
10
第四章 平稳时间序列模型的建立
对AR(1)模型,有
k , 1
20
第四章 平稳时间序列模型的建立
2. 对ARMAБайду номын сангаасn,m)模型
可看成n+m阶回归方程
检验ARMA(n,m)与ARMA(n-1,m-1)有无显著性差异
H0:无显著性差异
ARMA(n,m)
Q0:对应自由度为N-n-(n+m)=N-2n-m
ARMA(n-1,m-1)
Q1:对应自由度为N-(n-1)-(n+m-2)=N-2n-m+3
3. 残差方差的计算:
2 ˆa
Q 实际观察值个数-参数个数
Q 2 ˆa AR : (n) ( N n) (n 1) Q 2 ˆ MA : a (n) N (n 1) Q 2 ˆa (n, m) ARMA : ( N n) (n m 1)
8
第四章 平稳时间序列模型的建立
(1)序列均值的方差为: 对有N个观察值的有限时间序列( X 1 , X 2 ,, X N ),其 均值μ可用样本均值
X 1 N
N
X
t 1
t
来估计,且是μ的无偏估计。为度量其精度,我们有:
var(X ) 12 N
ts
t 1 s 1
N
N
k 1,2,, m
这是一个由m+1个方程构成的非线性方程组。 常用的求解方法有三种:直接法、线性迭代法和 Newton-Raphson算法。
33
第四章 平稳时间序列模型的建立
例:求MA(1) 模型参数的矩估计
1 1 4 12 1 2 1
1
2 1 1 1 4 12
14
第四章 平稳时间序列模型的建立
第二节
模型定阶
一、自相关和偏自相关函数定阶法
二、残差方差图定阶法 三、 F检验定阶法 四、 最佳准则函数定阶法(AIC、FPE、BIC准则)
15
第四章 平稳时间序列模型的建立
一、 自相关和偏自相关函数定阶法
AR(p)模型 MA(q)模型 ARMA模型 ρ k φ kk 拖尾 p步截尾 q步截尾 拖尾 拖尾 拖尾
1
又有
k1 1,k 2 2 ,,kk k ,
31
第四章 平稳时间序列模型的建立
又有:
2 0 1 1 2 2 n n a
可得:
2 ˆ1 ˆ 2 ˆ n ˆi ˆi ) ˆa ˆ0 ˆ1 ˆ2 ˆn ˆ0 (1 i 1 n
既不截尾也不拖尾:无上述特征,呈明显缓慢衰减或周 期性衰减。这说明序列是非平稳的。
13
第四章 平稳时间序列模型的建立
即如果自相关函数是q阶截尾的,当k>q时,自相 关估计值的方差满足
q 1 var(rk ) (1 2 v2 ) (k>q) N v 1 如果自相关估计值在 0 2 var(rk ) 范围内,可 看成是截尾的。
一、模型参数估计的几种方法
常用的参数估计方法有:
矩估计、极大似然估计、贝叶斯估计、
最小二乘估计等 二、模型参数的相关矩估计
29
第四章 平稳时间序列模型的建立
二、模型参数的相关矩估计
1. 矩估计:
用样本矩去估计总体相应的矩。
是一种简单粗略的估计,但可提供迭代估计时的初值 优点:简单易懂,便于计算 缺点:有效性和精度不够
例1:求AR(1)模型参数的矩估计
2 ˆ1 ˆ1; ˆ1 ˆ12 ) ˆa ˆ0 ˆ1 ˆ0 (1
32
第四章 平稳时间序列模型的建立
(2)MA模型参数的矩估计 在第三章考察模型的自协方差时我们得到:
2 2 0 (1 12 22 m ) a 2 k ( k k 11 k 2 2 m mk ) a
11
第四章 平稳时间序列模型的建立
2. 自相关和偏自相关函数估计值的截尾和拖尾性判断 在进行模型识别(主要是考虑自相关函数和偏自相关函 数的截尾和拖尾性)时,要用到自相关和偏自相关估计 的标准差
(1)自相关函数和偏自相关函数的估计值的渐近分布
q 2 1 自相关函数q步截尾, ˆ k ~ N 0, ˆ j ) (1 2 j 1 当k>q时,有 N
5
第四章 平稳时间序列模型的建立
2. 这种识别方法的优缺点: 优点:简单易懂,易于操作,应用广泛。 缺点:精度不够,特别是序列长度不足够长时。 这是因为
(1)识别时用的是自相关函数和自协方差函数的样本 估计值,它们与理论值有一定差异; ( 2 )对高阶 ARMA 模型的识别,显得有些力不从心。
改进措施:可利用自相关和自协方差函数做初步识别, 再结合其他方法确定模型。
34
第四章 平稳时间序列模型的建立
23
第四章 平稳时间序列模型的建立
2. 主要有AIC准则、FPE准则和BIC准则
3. FPE准则:
最小化最终预测误差(Final Prediction Error)准则
依据:
根据模型的预报误差来判断自回
归模型的阶数是否恰当。
适用范围:AR模型
24
第四章 平稳时间序列模型的建立
准则函数:
2 ˆ i ˆa ˆ0 ˆi ) FPE(n) N n N n ( N n N n i 1 n
2 ˆ 用AR(n)拟合序列{Xt},则拟合残差方差 a
2 ˆ 是n的函数,记作 a (n)
n
