浙江省2017年高中(高一)“希望杯”二试数学试题+Word版含答案

合集下载

第十五届“希望杯”数学竞赛第一试试题及答案整理

A. log3 x -1
-x
B. 2 - 3
C. 3-2+x
D. 2 - log3 x
A
4பைடு நூலகம்
40
二、组填空题（每题分，共分） 11 ．已知函数
f (x)
=
ì í
1,
x为有理数，
g(
x)
=
ì í
0,
x为有理数，
当
xÎR 时，
î0，x为无理数.
î1，x为无理数.
f (g (x)) = _______, g ( f( )x) = _ _ _ _ _ _ _ .
B. 减法 D. 除法
{ } 9．等比数列
an
中，“
a 1
<
a 3
”是“
a 7
<
a 9
”的（
）
A. 充分而不必要条件 B. 必要而不充分条件 C. 充要条件
D. 既不充分又不必要条件
10．已知函数 f (x) 的图象与函数 g(x) = 3x 的图象关于点 (0,1) 对称，则 f (x) =（）
4. 等差数列
{an
}
、
{bn}
的前
n
项的和分别为
Sn
、
Tn
，且
Sn Tn
=
3n - 3 ，则 a6 2n + 3 b6
=（
）
A. 3 2
B. 1
6
C.
5
27
D.
23
5. 如图，EF 是梯形 ABCD 的中位线，则在向量 1 ( AD + BC) 、
2
A
1 ( AC + BD) 、 1 (2AD - AB - CD) 中，与 EF 相等的向量的个 E

浙江省2017年高中(高二)“希望杯”二试数学试题+Word版含答案

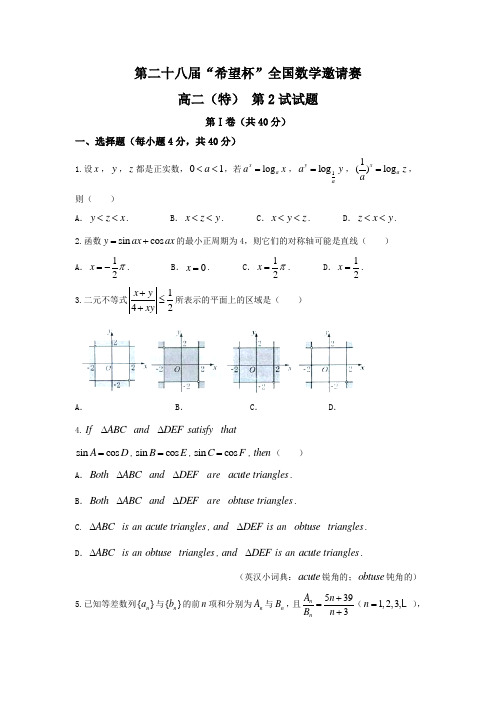
第二十八届“希望杯”全国数学邀请赛高二（特）第2试试题第Ⅰ卷（共40分）一、选择题（每小题4分，共40分）1.设x ，y ，z 都是正实数，01a <<，若log x a a x =，1log y aa y =，1()log xa z a=，则（）A ．y z x <<.B ．x z y <<.C ．x y z <<.D ．z x y <<. 2.函数sin cos y ax ax =+的最小正周期为4，则它们的对称轴可能是直线（） A ．12x π=-. B ．0x =. C ．12x π=. D ．12x =. 3.二元不等式142x y xy +≤+所表示的平面上的区域是（）A ．B ．C ．D ．4.If ABC ∆ and DEF ∆satisfy thatsin cos A D =,sin cos B E =,sin cos C F =,then （）A ．Both ABC ∆ and DEF ∆ are acute triangles .B ．Both ABC ∆ and DEF ∆ are obtuse triangles .C. ABC ∆ is an acute triangles ,and DEF ∆is an obtuse triangles . D ．ABC ∆ is an obtuse triangles ,and DEF ∆is an acute triangles .（英汉小词典：acute 锐角的；obtuse 钝角的）5.已知等差数列{}n a 与{}n b 的前n 项和分别为n A 与n B ，且5393n n A n B n +=+（1,2,3,n = ），则使nna b 为整数的正整数n 的个数是（） A ．3. B ．4. C.5. D ．6.6.在三棱锥VABC 中，AVB AVC ∠=∠，则VA BC ⊥是VB VC =的（ A ．充分不必要条件.B ．充要条件. C.必要不充分条件.D ．既不充分也不必要条件.7.For a tan rec gular triangle ABC in a Cartesian coordinate system ，there are (2,1)AB = ，(3,)AC m =，then the number of different possiblevalues of m is （）A ．0.B ．1. C.2. D ．3.8.一项“闯关”游戏的规则为：在桌面上抛掷一个各面内分别写有1,2,3，…，12的正十二面体n 次，若抛掷n 次后朝下的面内n 个数的和不小于211n +，则算过关，现有一人做此游戏，他最多只能连过（）A ．10关.B ．11关. C.12关. D ．13关. 9.The number of roots of the equation cos(cos )sin αα= inthe int erval ,22ππ⎡⎤-⎢⎥⎣⎦is （）A ．0.B ．1. C.2. D ．3.10.已知双曲线22221x y a b-=（0a >，0b >），若过右焦点F 且倾斜角为30︒的直线与双曲线的右支有两个交点，则此双曲线的离心率的取值范围是（） A ．（1,2）. B．. C.[2,)+∞. D．)+∞. 第Ⅱ卷（共90分）二、填空题（每小题4分，共40分.）11.集合{1,1,12}A d d =++，2{1,,}B r r =，若A B =，则r = ．12.已知方程24210x x --=的两个根为cos α，cos β，α，β(0,)π∈，则cos()αβ-= ．13.光线沿着直线3+1=0x y +射入，遇到直线210x y --=反射，则反射光线所在直线的方程是．14.已知整数a ，b ，c 满足22222874a b c ab b c +++<++，则a b c ++= ． 15.已知i x R +∈（1,2,,2017i = ）满足122017x x x ≥≥≥ ，122017420x x x +++= ，如果121()k k y x x x k=+++ （1,2,,2017k = ），则122017y y y +++ 的最小值是．16.已知数列{}n a ，满足11a =，11(21)n n n n a n a a a ++=++，则2017a = ． 17.数列2{lg(10002)}a- 的前n 项和为n S ，则使n S 取得最大值的n 的值是 .18.棱长为1的正方体1111ABCD A BC D -中，P 是棱11A B 上的动点，过点P 、B 、1D 作截面，则截面面积的最小值是 .19.正方形ABCD 的边长为a ，点A 和B 在抛物线2y x =上，点C 和D 在直线21y x =-上，则a = .20.已知圆C 经过双曲线22(2)(1)1916x y +--=的两个焦点，并且与x 轴交于M 、N 两点，若8MN =，则圆C 的方程是 .三、解答题每题要写出推算过程.21. 若正数a ，b ，c 满足1a b c ++=，求证：2221a b c +++.22. 如图，四面体ABCD 中，DA ⊥平面ABC ，AC BC ⊥，1DA AC ==，BC .（1）求异面直线AB ，CD 所成角的余弦值；（2）若E ，F 分别为AB ，CD 上的点，且满足,AE AB CF CD λλ==，01λ<<.若EF与平面ABC 所成角为α，求sin α的最大值.23.数列{}n a 中，已知13a =，2112(1)n n n a a a --=-（2n ≥）.（1）判断数列{}n a 的单调性，并证明你的结论；（2）若数列{}n b 满足2n n n a b a =-（n N +∈），求数列{}n b 的通项公式.试卷答案一、选择题1-5:DDBDC 6-10:BCBBB二、填空题11.12-13.91330x y ++=14.415.420 16.21201717.1918.219.20.22(2(5)41x y ++-=）三、解答题21.原不等式等价于2222()a b c a b c +++≤++，ab bc ca ++，即23()abc ab bc ca ≤++222222=2()a b b c c a abc a b c +++++，也即222222abc a b b c c a ≤++，（*）又222222a b b c b ac +≥，222222b c c a c ab +≥， 222222c a a b a bc +≥，上面三式相加即得（*）. 故待证不等式成立.22.（1）作CG ⊥平面ABC ，以CA ，CB ，CG分别为x 轴、y 轴、z 轴建立空间直角坐标系.则cos ,||||AB CDAB CD AB CD <>=6==-所以，异面直线AB ，CD所成角的余弦值为6（2）FE FA AE =+()FC CA AE =++ ()CF CA AE =-++ CD CA AB λλ=-++(1,0,1)(1,0,0)(1λλ=-++-(21,)λλ=-+-.易知，平面ABC 的法向量(0,0,1)n =.于是||sin |cos ,|||||FE n FE n FE n α=<>====≤. 当12λ=，即12λ=时，等号成立. 所以sin α的最大值是3. 23.（1）数列{}n a 是递减数列. 首先，由数学归纳法易证2n a >（n N +∈）又212(1)nn n n n a a a a a +-=--221112(1)21n n n n n a a a a a ⎛⎫-+==-+ ⎪--⎝⎭，由2n a >，得111n a <-，即1121n n a a +<<-，所以10n n a a +-<，故数列{}n a 是递减数列. （2）1112n n n a b a +++=-222(1)22(1)nn nn a a a a -=-- 222(2)n nn a b a ==-，又11132a b a ==-，所以2224122()n n n n b b b b ---===11822312n n n b b ---==== ，即123n n b -=.。

2017浙江省高中数学竞赛试卷含答案

a 2 +1⎩ 2017 年浙江省高中数学竞赛一、填空题：本大题共 10 个小题,每小题 8 分,共 80 分.1.在多项式(x -1)3(x + 2)10 的展开式中 x 6 的系数为．2.已知log (5a - 3) = log5 , 则实数 a = ．3.设 f (x ) = x 2+ ax + b 在[0,1]中有两个实数根,则a 2- 2b 的取值范围为．4. 设 x , y ∈ R ,且sin 2 x - cos 2 x + cos 2 x cos 2 y - sin 2 x sin 2 ysin(x + y )= 1 ,则x - y = ．5. 已知两个命题,命题 p :函数 f (x ) = log a x ( x > 0 )单调递增；命题q ：函数g (x ) = x 2 + ax +1 （ x ∈ R ）．若 p ∨ q 为真命题， p ∧ q 为假命题，则实数a 的取值范围为．6. 设S 是(0, 5) 中所有有理数的集合，对简分数 q ∈ S ，( p , q ) = 1，定义函数 f ( q ) = q +1 ， 8 p p p则 f (x ) = 2在 S 中根的个数为．37.已知动点 P ，M ，N 分别在 x 轴上，圆(x -1)2 + ( y - 2)2 = 1 和圆(x - 3)2 + ( y - 4)2 = 3上，则| PM | + | PN | 的最小值为．8.已知棱长为 1 的正四面体 P - ABC ，PC 的中点为 D ，动点 E 在线段 AD 上，则直线 BE 与平面 ABC 所成的角的取值范围为．9.已知平面向量a ， b ， c ，满足| a |= 1，| b |= 2 ，| c |= 3 ， 0 < λ < 1，若b ⋅ c = 0 ，则| a - λb - (1- λ)c | 所有取不到的值的集合为．⎧-2x , x < 0, 10.已知 f (x ) = ⎨x 2 -1, x ≥ 0, 方程 f (x ) + 2 1- x 2+ | f (x ) - | -2a * 4 = 0 有三个根 x 1 < x 2 < x 3 ．若 x 3 - x 2 = 2(x 2 - x 1 ) ，则实数 a = ．二、解答题：本大题共 5 个小题，满分 120 分，将答案填在答题纸上）11.设 f 1 (x ) ，f n +1 (x ) ，n = 1 ，2，…．对每个n ，求 f n (x ) = 3x 1- x 2 x 2 + 32 x 2 + 16 f (x ) 3n7y n的实数解．x 212.已知椭圆 2 + = 1的右焦点为 F ，过 F 的直线 y = k (x - 2) 交椭圆于 P ， Q 两点 6 2(k ≠ 0) ．若 PQ 的中点为原点，直线ON 交直线 x = 3 于 M ．（1）求∠MFQ 的大小； PQ（2）求MF的最大值．13.设数列{a n } 满足：| a n +1 - 2a n |= 2 ，| a n |≤ 2 ， n = 1,2,3，…．证明：如果a 1 为有理数，则从某项后{a n } 为周期数列．14.设a ， a ， a ； b ， b ， b ∈ Z + ，证明：存在不全为零的数λ ， λ ， λ ∈{0,1, 2}，123123123使得λ1a 1 + λ2 a 2 + λ3a 3 和λ1b 1 + λ2b 2 + λ3b 3 同时被 3 整除．15.设σ = {a 1, a 2,…,a n }为{1, 2,…, n }的一个排列，记 F (σ ) =∑a i a i +1 ， a n +1 = a 1 ，求i =1min F (σ ) ．3x 2 + 8x 2 x 2 + 32 x 2 +1 2017 年浙江省高中数学竞赛答案一、填空题1. -41282.23. [0, 2]4.2k π + π（ k ∈ Z ） 5. (-2,1] [2, +∞)26.57. 2- -1 8. ⎡0, arctan 14 ⎤⎢ 7⎥ ⎣ ⎦69. (-∞,13 -1) (4, +∞) 10.132三、解答题11.证明：利用数学归纳法．（1） x = 2 是 f n (x ) = 3x 的解．当 n = 1 时， x = 2 是 f 1 (x ) = = 3x 的解.当 n = k 时，设 f k (2) = 6 ，则 f k +1 (2) = = 6 . 由此可得 x = 2 是 f n (x ) = 3x 的解（对于所有的n ）.（2）当 x > 2 时， f n当 n = 1 时， f 1 (x ) = (x ) < 3x < 3 x 2． 2< 3x < 3 x 2(x > 2) ． 2当 n = k 时，设 f k (x ) < 3x < 3x 2，则 f 2k +1(x )< = 3x ．由此可得 x > 2 都不是 f n (x ) = 3x 的解（对于所有的n ）．（3）当0 < x < 2 时， f n (x ) > 3x ．当 n = 1 时， f 1 (x ) = > = 3x （ 0 < x < 2 ）.当 n = k 时，设 f k (x ) > 3x ，则 f k +1 (x ) = > > 3x ．由此可得0 < x < 2 都不是 f n (x ) = 3x 的解（对于所有的n ）．因此，对每个n ， f n (x ) = 3x 的实数解为 x = 2 ．10 17 - 3x 2 + 32 4 + 16 f (2) 3kx 2 + 32x 2 + 16 f (x ) 3k x 2 + 8x 2 x 2+ 16 f (x ) 3k3 ⎪ 12k 1 ⎣ ⎦+ = ⎧ x 2 y 2 12.解：（1）联立⎨ 6 2 1, 可得(3k 2 +1)x 2 -12k 2 x +12k 2 - 6 = 0 ． ⎪⎩ y = k (x - 2),设 P 点的坐标为(x p , y p ) ， Q 点的坐标为(x q , y q ) ，2 则 x p + x q = 3k 2 +1 ， x p x q = 12k 2 - 6 3k 2+1． -4k于是有 y p + y q = k (x p + x q ) - 4k =3k 2+1．因为 PQ 的中点为 N ，所以 N ( 6k 22 -2k 2 ) ，因此ON 的斜率k =- 1，3k +1 3k +1 3k因为直线ON 交直线 x = 3 于 M ，所以 M (3, - 1) ，故 MF 的斜率为k k MF=- ， k即得k MF ⋅ k PQ= -1，因此 MF 与 PQ 垂直， ∠MFQ = π． 2PQ (x - x )2 + k 2 (x - x )2（2） I = ( )2 = p q pq = k 2 (x p - x q )2 = k 2 ⎡⎣(x p + x q )2 - 4x p x q ⎤⎦ MF2 ⎡ 144k 41+ 1k 2 2k 2 -1⎤2 k 2 +1= k ⎢(3k 2 +1)2 - 24 3k 2 +1⎥ = 24k (3k 2 +1)2．令u = 3k 2 +1，则 I = 8 (u -1)(u + 2) = - 16 ( 1 - 1 - 1) = - 16 ⎡( 1 - 1 )2 - 9 ⎤，3u 2由于u = 3k 2 +1 > 1，故0 ≤ 1< 1 .u3 u 22u 23 ⎢⎣ u416 ⎥⎦因此 I max = 3 （当u = 4 时取到最大值，也即k = ±1 ）． PQ综上所述，的最大值为．MF13.证明：（1）若a 1 为有理数，则{a n } 为一个有理数数列．（2）对于任意的n ，设a n2 y + 2x = y， ( y , x ) = 1，由已知条件，有且仅有下述一个等式成立： x2 y - 2xa n +1 = 2a n + 2 = x 或 a n +1 = 2a n - 2 =． (*) xa n 与 a n +1 有相同的分母（不进行约分）．（3）设a =q， ( p , q ) = 1，则a =b n， b 为整数，由于| a|≤ 2 ， n = 1，2,3，…，因1pnpn nON ,此-2 p ≤ b n ≤ 2 p ．（4）若存在两个自然数k < l ，使得a k = a l ，则由（2）中得到的（*）递推公式以及| a n |≤ 2 ，n = 1,2,3，…，可得{a n }从第k 项开始是一个周期数列，周期为l - k ．（5）由（3）可知对于任意的n ，b n 的值只有4 p +1（有限个），故总能找到k < l ，使得b k = b l ，从而有a k = a l ．综上所述，如果a 1 为有理数，则从某项后{a n } 为周期数列．14.证明：不妨设a i ≡ k k (mod 3) ， b i ≡ l i (mod 3) ， k i ， l i ∈{0,1, 2} ， i = 1, 2, 3 ．则要证明结论正确，只要证明存在不全为零的数λ1 ， λ2 ， λ3 ∈{0,1, 2}，使得λ1k 1 + λ2k 2 + λ3k 3 ≡ λ1l 1 + λ2l 2 + λ3l 3 (mod 3) ≡ 0(mod 3) ．(*)记 k 1l 2 - k 2l 1 = c (mod 3) ，这里c ∈{0,1, 2}．情形（1）当c = 0 时，则k 1 = l 1 = 0 ，或者k 1 ， l 1 不全为零．若 k 1 = l 1 = 0 ，则取λ1 = 1， λ2 = λ3 = 0 ，有（*）式成立．若 k 1 ， l 1 不全为零，不妨设k 1 ≠ 0 ，则取λ1 = k 2 , λ2 = -k 1 , λ3 = 0 ,且⎧λ1k 1 + λ2k 2 + λ3k 3 = k 2k 1 - k 1k 2 ≡ 0(mod 3),⎨λ l + λ l + λ l = k l - k l ≡ 0(mod 3), 即(*)式. ⎩ 1 1 2 2 3 3 2 1 1 2情形（2）当c = 1 或 2 时，即c 2 ≡ 1(mod 3) ．记c (k 2l 3 - k 3l 2 ) ≡ c 1(mod 3) ， c (k 3l 1 - k 1l 3) ≡ c 2 (mod 3) ，这里c 1 ， c 2 ∈{0,1,2} ．令λ1 = c 1 ， λ2 = c 2 ， λ3 = 1，则λ1 ， λ2 ， λ3 ∈{0,1, 2}且不全为零，且λ1k 1 + λ2 k 2 + λ3k 3 = c 1k 1 + c 2k 2 + k 3 ≡ c (k 2l 3 - k 3l 2 )k 1 + c (k 3l 1 - k 1l 3 )k 2 + k 3 (mod 3)≡ ck (k l - k l ) + k (mod 3) ≡ (1- c 2 )k (mod 3) ≡ 0(mod 3) ，32 11 233类似可以证明λ1l 1 + λ2l 2 + λ3l 3 ≡ 0(mod 3) ．综上所述，可以取到不全为零的数λ1 ， λ2 ， λ3 ∈{0,1, 2}，使得（*）式成立． 15.解：问题等价于圆周上放置n 个数，使得相邻数的乘积之和为最小，最小值记为T n ．n⎨ n不妨设a 1 = n ，则数字 1 必与它相邻，否则设a j = 1（ j ≠ 2 ，n ），则可将 a 2 ，a 3 ，…，a j的数字改变为a j ， a j -1 ，…， a 2 上的数字，则相邻数的乘积和的该变量为a 1a j + a 2a j +1 - a 1a 2 - a j a j +1 = (a 1 - a j +1 )(a j - a 2 ) < 0 ．于是可确定a 2 = 1．再说明数字 2 也必与数字n 相邻，即a n = 2 ．事实上，若a j = 2 （ j ≠ n ），则交换a n ， a n -1 ，…， a j 为a j ， a j +1 ，…， a n ，此时的目标改变值为a 1a j + a n a j -1 - a 1a n - a j a j -1 = (a 1 - a j -1 )(a j - a n ) < 0 ．因此目标取到最小值时， a 1 = n ， a 2 = 1， a n = 2 ．由此出发，依次可得 a 3 = n -1 ，a n -1 = n - 2 ．在已安排好的两端数字，若剩下的数比两端数字都小，则在剩下的数中找两个最小的数字，按小对大，大对小放置；若剩下的数比两端数字大，则在剩下的数字中找两个最大的数，按大对小，小对大放置．由此规律即得a 4 = 3 ， a n -2 = 4 ， a 5 = n - 3 ， a n -3 = n- 4 ，…．下面用递推法计算T n ．考虑n + 2 个数字，我们在T n 的数字排序中，将每个数字加 1，再放置 1，n + 2 这两个数字，在2 ， n +1的中间插入n + 2 ，1，即可得到T n +2 ．因此， T n +2 = T n '+ (n +1) + (n + 2) + 2(n + 2) - 2(n +1) ，其中T n ' =∑(a i+1)(ai +1+1) = T n + n (n + 2) ，i =1由此可得T n +2 = T n + n 2 + 4n + 5 ，⎧1 n 3 + 1 n 2 + 5n -1, n = 2m , 可以推出T = ⎪6 2 61 1 5 1 ⎪ n 3 + n2 + n - , n = 2m -1. ⎪⎩62 6 2。

[高二]希望杯数学竞赛试题(第二届第2试)

第二届“希望杯”全国数学邀请赛高二第2试一、选择题1.映射:(,,,)(1,2,3)f a b c d →，如果10()()()()20f a f b f c f d <<，这样的映射共有A．23个 B．24个 C．25个 D．26个 2.曲线22116x y k k−=−与曲线22925225x y +=的焦距相等的充要条件是 A．16k <且0k ≠ B．0k >且16k ≠ C．016k << D．0k <或16k >3.定义在全体实数上的函数()f x ，满足：（1）33()()f x f x =（2）对任意12x x ≠，都有12()()f x f x ≠.则(1)(0)(1)f f f −++的值是A．0 B．1 C．-1 D．不能确定4.正方体表面正方形的对角线所在直线中有两条直线的距离是1，则此正方体的体积是A．1 B．或5. 33{(,)862,,}M x y x y xy x y R ==++≥∈，222{(,)8,,0}P x y x y t t R t ==+≤∈≠，若P M =∅∩，则有A．11t −<< B．44t −<< C．55t −<< D．1122t −<< 6.函数()arcsin(cos )arccos(sin )f x x x =+的值域是 A．3[,]22ππ− B．3[0,]2π C．[,]2ππ− D．[0,]π 7.把函数1()y f x −=的图象在坐标轴内以原点为旋转中心按逆时针方向旋转90度，得到A．()y f x =− B．()y f x =− C．1()y fx −=− D．()y f x =−− 8.过(,0)A p 作抛物线222(0)y p px p +=>的与对称轴垂直的弦12,PP O 为原点，则12POP ∠是A．直角 B．钝角 C．锐角 D．不确定9.设()arccos 2arcsin f x x x =+，则1()fx −是 A．sin ,[,]22x x ππ∈− B．cos ,[0,]x x π∈ C．sin ,[,]22x x ππ−∈− D．cos ,[0,]x x π−∈ 10.设,,||1,||1x y R x y ∈<<，记[]x 表示不超过x 实数的最大整数，则不等式[][][]x y x y +≤+的解集区域图是（此题改为作图题，选项略去）二、填空题11．集合{(,)||6||12||12|2|3|15,,}M x y x y x y x y R =−++=−++=∈中的元素的个数是_____.12．已知台体上、下底的面积分别为12,S S ，若与底面平行的平面把台体截成体积相等的两部分，则截面面积为_____.13．方程330x −=的全部负根之和是_____.14．以实数,x y 为自变量的函数2(,)u x y x =+15．过圆222610x y x y ++−+=与圆2266170x y x y +−−+=的交点的直线方程可表示为_____.16．{}x 表示不小于实数x 的最小整数，则222{log 1}{log 2}{log 1991}+++= _____. 17．函数arcsin arccos x y x=的值域是_____. 18．()f x 对任意12,x x R ∈都有1212()()()f x x f x f x −=+，则它的奇偶性是_____.19．定义在正整数上且函数值总是自然数的严格增函数()f n ，对任意,m n N +∈，当,m n 的最大公约数是1时，()()()f mn f m f n =×．若(180)180f =，则(1991)f =_____.20．正十二面体有20个顶点，30条棱，每一个顶点是3条棱的交点，这三条棱的另一个端点是正十二面体的另外3个顶点，我们称这3个顶点与前一个顶点是相邻的．在每个顶点处放上一个实数，要求每个顶点所放的实数恰是该顶点相邻的3个顶点处所放实数的算术平方值．设,M m 分别是这20个实数中最大的和最小的，则M m −的取值范围是_____.三、解答题21．直角三角形ABC 中AB AC =．用C 点为一个焦点作一个椭圆，使这个椭圆的另一个焦点在AB 边上，且椭圆过,A B 点．求这个椭圆的离心率．22．已知正四面体ABCD ，考察下列集合．X ：与四面体四个顶点的距离都相等的平面； Y ：X 中任意两平面的交线；Z ：Y 中任意两直线的交点；求：Z 中包含的元素数目，并指出Z 中各元素在空间的位置（也可画出Z 中各元素的空间位置并加以说明）．。

高中一年级第2试

３×４２０＋２，４×４２０＋２，即共有５个符合题意的自然数，其中最大的自然数是４×４２０＋２＝１６８２．２３．当ｂ＝０时，｜ｘ２－１｜＝１１０ｘ，此时要求ｘ≥０，去掉绝对值，解一元二次方程得ｘ＝－１±槡４０１２０或ｘ＝１　±槡４０１２０，舍去两负根，因此Ａ中只有２个元素．当ｂ＝１时，｜ｘ２－１｜＝１１０ｘ＋１，此时要求ｘ≥－１０，去掉绝对值，解一元二次方程得ｘ＝０，－１１０或１　±槡８０１２０．它们都满足ｘ≥－１０，因此Ａ中有４个元素．２４．ａｎ＝｛２，４，８，１６，３２，６４，１２８，２５６，５１２，…｝，若｛ａｎ｝中的元素在｛ｃｎ｝中，则必须满足减２以后能被３整除，则只有８，３２，１２８，５１２，…满足条件，即２３，２５，２７，２９，…故ｃｎ＝２２ｎ＋１，即公比ｑ＝２２（ｎ＋１）＋１２２ｎ＋１＝２２ｎ＋３２２ｎ＋１＝４，所以Ｓｎ＝８（１－４ｎ）１－４＝８３（４ｎ－１）．２５．第ｎ组中有２ｎ－１个数对，则前ｎ组共有１＋３＋５＋…＋（２ｎ－１）＝ｎ２个数对．因为４４２＝１９３６＜２００５＜４５２＝２０２５，所以２００５在第４５组．因为前４４组共有１９３６个数对，且２００５－１９３６＝６９，所以第２００５个数对是第４５组中的第６９个数对．观察规律可知，由于４５为奇数，所以第一个数对为（０，４４），数对中的第一个数逐步增加到４４，即第４５个数对为（４４，４４），然后第二个数４４逐步减去１，所以第４５组中第６９个数对是（４４，２０）．高中一年级第２试一、选择题１．已知等差数列｛ａｎ｝中（ａｎ∈Ｚ，ｎ∈Ｎ＊），ａ１＝５，ａ２＝ｂ，则ａｎ≠０的充要条件为（）（Ａ）ｂ≠０．（Ｂ）ｂ≠４．（Ｃ）ｂ≠０或ｂ≠４．（Ｄ）ｂ≠０且ｂ≠４．２．对１９４９°，１９６６°，２００５°，２００８°依次求余弦，则余弦值最大及最小的角依次是（）（Ａ）１９４９°，１９６６°．（Ｂ）１９６６°，１９４９°．（Ｃ）２００８°，１９６６°．（Ｄ）２００５°，２００８°．３．下列函数中，值域为Ｒ＋的是（）（Ａ）ｙ＝２－｜ｘ－１｜．（Ｂ）ｙ＝３ｘ＋１（ｘ＞０）．（Ｃ）ｙ＝ｘ２＋ｘ＋２．（Ｄ）ｙ＝１ｘ２．４．设集合Ｍ＝ｘ　ｘ＝ｋ２＋１４，ｋ∈Ｚ｛｝，Ｎ＝ｘ　ｘ＝ｋ４＋１８，ｋ∈Ｚ｛｝，Ｐ＝ｘ　ｘ＝ｋ８＋１４，ｋ∈Ｚ｛｝，则下面的结论中正确的是（）（Ａ）Ｍ∪Ｎ＝Ｐ．（Ｂ）Ｍ∩Ｎ＝Ｐ．（Ｃ）Ｍ∩Ｐ＝Ｐ．（Ｄ）Ｍ∩Ｎ＝Ｍ．５．偶函数ｆ（ｘ）（ｘ∈Ｒ）满足：ｆ（－４）＝ｆ（１）＝０，在区间［０，３］与［３，＋∞）上分别递减和递增，则不等式ｘ３　ｆ（ｘ）＜０的解集为（）（Ａ）（－∞，－４）∪（４，＋∞）．（Ｂ）（－４，－１）∪（１，４）．（Ｃ）（－∞，－４）∪（－１，０）．（Ｄ）（－∞，－４）∪（－１，０）∪（１，４）．·１４·６．如果ｆ（ｘ）＝ｍａｘ｛ｓｉｎｘ，ｃｏｓｘ｝（ｘ∈Ｒ），则下面命题正确的是（）（Ａ）函数ｆ（ｘ）的值域是［－１，１］．（Ｂ）当且仅当ｘ＝２ｋπ＋π２（ｋ∈Ｚ）时，ｆ（ｘ）取得最大值．（Ｃ）函数ｆ（ｘ）的最小正周期是π．（Ｄ）当且仅当２ｋπ＋π＜ｘ＜２ｋπ＋３π２（ｋ∈Ｚ）时，ｆ（ｘ）＜０．７．Ｆｏｕｒ　ｐｅｏｐｌｅ，Ａ，Ｂ，Ｃａｎｄ　Ｄａｒｅ　ａｃｃｕｓｅｄｉｎ　ａ　ｔｒｉａｌ．Ｉｔ　ｉｓ　ｋｎｏｗｎ　ｔｈａｔ（１）ｉｆ　Ａｉｓ　ｇｕｉｌｔｙ，ｔｈｅｎ　Ｂｉｓ　ｇｕｉｌｔｙ；（２）ｉｆ　Ｂｉｓ　ｇｕｉｌｔｙ，ｔｈｅｎ　Ｃｉｓ　ｇｕｉｌｔｙ　ｏｒ　Ａｉｓｎｏｔ　ｇｕｉｌｔｙ；（３）ｉｆ　Ｄｉｓ　ｎｏｔ　ｇｕｉｌｔｙ，ｔｈｅｎ　Ａｉｓ　ｇｕｉｌｔｙ　ａｎｄＣｉｓ　ｎｏｔ　ｇｕｉｌｔｙ；（４）ｉｆ　Ｄｉｓ　ｇｕｉｌｔｙ，ｔｈｅｎ　Ａｉｓ　ｇｕｉｌｔｙ．Ｈｏｗ　ｍａｎｙ　ｏｆ　ｔｈｅ　ａｃｃｕｓｅｄ　ａｒｅ　ｇｕｉｌｔｙＡｎｓｗｅｒ：（）（Ａ）２．（Ｂ）３．（Ｃ）４．（Ｄ）Ｉｎｓｕｆｆｉｃｉｅｎｔ　ｉｎｆｏｒｍａｔｉｏｎ　ｔｏ　ｄｅｔｅｒｍｉｎｅ．８．已知ｆ１（ｘ）＝ｘ＋１，ｆ２（ｘ）＝２ｘ，ｆ３（ｘ）＝－３ｘ＋５，Ｆ（ｘ）＝ｍｉｎ｛ｆ１（ｘ），ｆ２（ｘ），ｆ３（ｘ）｝，则Ｆ（ｘ）的最大值为（）（Ａ）１．（Ｂ）２．（Ｃ）４．（Ｄ）８．９．满足ａ２－３ｂ－９＝０（ａ，ｂ∈Ｚ），且｜ｂ｜≤１０００的数组（ａ，ｂ）的个数是（）（Ａ）５７．（Ｂ）５４．（Ｃ）３７．（Ｄ）１０９．１０．有“黄河源头第一县”之称的青海省果洛藏族自治州玛多县，被称作“千湖之县”．受连续干旱影响，该县有数百个湖泊相继干涸，且鼠害十分猖獗，草原在加速退化，每年因鼠害造成的退化面积达２０％．按这样的退化速度，自２００５年起，经过（）草原退化总面积将开始超过２００５年草原总面积的一半．（Ａ）３年．（Ｂ）４年．（Ｃ）５年．（Ｄ）６年．二、填空题１１．设集合Ａ＝｛１，２，３，４，５，６｝，则从Ａ到Ａ的映射ｆ有个，其中，满足ｆ（Ａ）≥ａ的映射有个．１２．若ｆ（ｘ）＝ｘ＋１，１，烅烄烆ｘ≥０，ｘ＜０．则ｆ（ｃｏｓ２）＝；当ｘ∈［０，２π）且满足ｃｏｓｘ＋ｆ（ｓｉｎｘ）＞１的ｘ的集合为．１３．一个三位数与它的各位数字和的比值为ｐ（例如对于三位数４６２，ｐ＝４６２４＋６＋２＝７７２），若三位数的各位数字都不为０，则当ｐ取得最小值时，此三位数是；当ｐ取得最大值时，此三位数是．１４．函数ｙ＝３ｘ２－６ｘ＋２　２ｘ－ｘ槡２＋４的最大值为，最小值为．１５．如果△ＡＢＣ边上的点的坐标（ｘ，ｙ）在映射ｆ：（ｘ，ｙ）→（２ｘ＋２，２ｙ－５）的作用下的像的集合所对应的图形是△Ａ′Ｂ′Ｃ′，已知△ＡＢＣ的面积为６，则△Ａ′Ｂ′Ｃ′的面积等于．１６．Ｌｅｔ　ａａｎｄ　ｂ　ｂｅ　ｔｈｅ　ｔｗｏ　ｒｅａｌ　ｒｏｏｔｓ　ｏｆｔｈｅ　ｑｕａｄｒａｔｉｃ　ｅｑｕａｔｉｏｎ　ｘ２－（ｋ－１）ｘ＋ｋ２＋３ｋ＋４＝０，ｗｈｅｒｅ　ｋ　ｉｓ　ｓｏｍｅ　ｒｅａｌ　ｎｕｍ　ｂｅｒ．Ｔｈｅｌａｒｇｅｓｔ　ｐｏｓｓｉｂｌｅ　ｖａｌｕｅ　ｏｆ　ａ２＋ｂ２　ｉｓ．１７．某校高一新生共有７８４人，每班分配５６人．方法是：将每人的入学成绩从高分到低分依次编号（成绩相同的学生按姓氏笔画的顺序），然后按Ｓ形顺序编班．例如：若有８个班，按编号１至８号分别编在１至８班，９至１６号分别编在８至１班，１７至２４号分别编在１至８班……．该校高一新生中编号为３００（每号只对应１人）的同学编在班．１８．函数ｙ＝ｘ２（－２≤ｘ≤２）与函数ｙ＝ｘ＋ｍ的图象恰有１个公共点在ｙ轴的右侧，则·２４·ｍ的取值范围是．１９．数列｛ａｎ｝的前三项依次为５，５５，５５５，但第４项不是５５５５，请写出一个适合题意的通项公式：ａｎ＝．２０．集合Ｍ＝｛ｘ｜ｘ＝９ｎ，ｎ＝０，１，２，…，２００５｝，已知９２００５是１９１４位数，则在Ｍ中最高位是９的数共有个．图１三、解答题２１．如图１所示，在凸四边形ＡＢＣＤ中，ＡＢ＝５，ＢＣ＝ＣＤ＝ＤＡ＝２，∠Ａ＝θ．（１）求ＢＤ的长（用θ表示）；（２）设△ＡＢＤ的面积为Ｓ１，△ＢＣＤ的面积为Ｓ２，ｆ（θ）＝Ｓ２１＋Ｓ２２，求函数ｆ（θ）的值域．２２．密码员王超设计了一种给自然数编码的方法：（１）先将自然数表示成五进制数（逢五进一）；（２）再将五进制中的５个数码与集合｛Ｖ，Ｗ，Ｘ，Ｙ，Ｚ｝中的元素建立一个一一对应关系．后来，他发现三个递增的相邻的十进制自然数被编成ＶＹＺ，ＶＹＸ，ＶＶＷ．求被编成ＶＷＸＹＺ的数所对应的十进制数．２３．已知函数ｆ（ｘ）＝ｘ２＋ｋｘ＋１ｘ２＋ｘ＋１．（１）当ｋ＝２时，求ｆ（ｘ）的值域；（２）若存在实数ａ，ｂ，ｃ，使ｆ（ａ）＋ｆ（ｂ）＜ｆ（ｃ），求实数ｋ的取值范围．参考答案一、选择题１．等差数列公差ｄ＝ｂ－５．如果等差数列不存在值为零的项，那么对于任意非零自然数ｎ，不等式５＋（ｎ－１）（ｂ－５）≠０恒成立，即ｎ≠５５－ｂ＋１Ｎ＊，所以５－ｂ≠１且５－ｂ≠５，即ｂ≠４，且ｂ≠０．反之，可证当ｂ≠４且ｂ≠０时，５５－ｂ＋１Ｎ＊，即对于任意非零自然数ｎ，当ｂ≠４且ｂ≠０时，不等式５＋（ｎ－１）（ｂ－５）≠０恒成立．所以这个数列中不存在零项的充要条件为ｂ≠０且ｂ≠４．故选（Ｄ）．２．ｃｏｓ１９４９°＝ｃｏｓ１４９°，ｃｏｓ１９６６°＝ｃｏｓ１６６°，ｃｏｓ２００５°＝ｃｏｓ２０５°＝ｃｏｓ１５５°，ｃｏｓ２００８°＝ｃｏｓ２０８°＝ｃｏｓ１５２°，在区间（９０°，１８０°）内，余弦函数是减函数，故ｃｏｓ１４９°＞ｃｏｓ１５２°＞ｃｏｓ１５５°＞ｃｏｓ１６６°，故选（Ａ）．３．ｙ＝２－｜ｘ－１｜的值域是（０，１］；ｙ＝３ｘ＋１（ｘ＞０）的值域是（１，＋∞）；ｙ＝ｘ２＋ｘ＋２的值域是７４，＋∞［）．故选（Ｄ）．４．因为Ｍ＝ｘ｜ｘ＝ｋ２＋１４，ｋ∈Ｚ｛｝＝ｘ｜ｘ＝２（２ｋ＋１）８，ｋ∈Ｚ｛｝，Ｎ＝ｘ｜ｘ＝ｋ４＋１８，ｋ∈Ｚ｛｝＝ｘ｜ｘ＝２ｋ＋１８，ｋ∈Ｚ｛｝，Ｐ＝ｘ｜ｘ＝ｋ８＋１４，ｋ∈Ｚ｛｝＝ｘ｜ｘ＝ｋ＋２８，ｋ∈Ｚ｛｝，所以Ｍ∪Ｎ≠Ｐ，Ｍ∩Ｎ≠Ｐ，Ｍ∩Ｎ＝，·３４·故排除（Ａ），（Ｂ），（Ｄ），又ＭＰ，所以Ｍ∩Ｐ＝Ｍ．故选（Ｃ）．５．由偶函数性质及单调性，知图２ｆ（－４）＝ｆ（－１）＝ｆ（１）＝ｆ（４）＝０，画出ｆ（ｘ）对应的大致图象，如图２所示．当ｘ＜－４或－１＜ｘ＜１或ｘ＞４时，ｆ（ｘ）＞０；当－４＜ｘ＜－１或１＜ｘ＜４时，ｆ（ｘ）＜０．当ｘ＜０时，ｘ３＜０；当ｘ＞０时，ｘ３＞０．所以ｘ３　ｆ（ｘ）＜０的解集为｛ｘ｜ｘ＜－４或－１＜ｘ＜０或１＜ｘ＜４｝．故选（Ｄ）．图３６．作出函数ｆ（ｘ）的图象，如图３所示，只有（Ｄ）是正确的．７．从Ｄ入手，分有罪和无罪两种情况讨论：假设Ｄ无罪，由（３）知，Ａ犯罪且Ｃ无罪；由（１）知，Ｂ犯罪．由（２）知，Ａ无罪或Ｃ犯罪，与Ａ犯罪且Ｃ无罪矛盾，故假设Ｄ无罪不成立，即Ｄ犯罪．由（４）知，Ａ犯罪；由（１）知，Ｂ犯罪；由（２）知，Ｃ也犯罪．因此犯罪的共有４人．故选（Ｃ）．８．如图４所示，作出ｆ１（ｘ），ｆ２（ｘ），ｆ３（ｘ），易得Ｆ（ｘ）的图象．由Ｆ（ｘ）的图象，可知Ｆ（ｘ）的最大值为２．故选（Ｂ）．图４９．由ａ２－３ｂ－９＝０，得ｂ＝ａ２３－３．①由｜ｂ｜≤１０００，有－１０００≤ａ２３－３≤１０００，０≤ａ２≤３００９，所以－槡３００９≤ａ≤槡３００９．因为ａ是整数，所以－５４≤ａ≤５４．②因为ｂ是整数，即ａ２３－３是整数，所以ａ２是３的倍数，即ａ·ａ３是整数，所以ａ是３的倍数．结合②知，ａ的值为－５４，－５１，－４８，…，５１，５４共３７个．故选（Ｃ）．１０．设２００５年的草原总面积为ｘ，设经过ｍ年后（即２００５＋ｍ年），草原的面积退化超过ｘ２，即１５ｘ＋１５×４５ｘ（）＋１５×４５（）２ｘ＋…＋１５×４５（）ｍ－１ｘ＞ｘ２，即４５（）ｍ＜１２．当ｍ＝３时，４５（）３＝６４１２５＞１２；·４４·当ｍ＝４时，４５（）４＝２５６６２５＜１２．所以最多经过４年，草原退化总面积就超过２００５年草原总面积的一半．故选（Ｂ）．二、填空题１１．（１）如图５所示，其它元素也如此，因此，从Ａ到Ａ的映射ｆ共有６×６×６×６×６×６＝６６（个）．图５图６（２）如图６所示，其它元素也如此，因此，满足ｆ（Ａ）≥ａ的映射共有１×２×３×４×５×６＝７２０（个）．１２．因为ｃｏｓ２＜０，所以ｆ（ｃｏｓ２）＝１，因此，原不等式等价于ｓｉｎｘ≥０，ｃｏｓｘ＋ｓｉｎｘ＋１＞１，烅烄烆或ｓｉｎｘ＜０，ｃｏｓｘ＋１＞１，烅烄烆解得０≤ｘ＜３π４或３π２＜ｘ＜２π．故满足条件的ｘ的集合为０，３π４［）∪３π２，２π（）．１３．设此三位数为ａｂｃ，则ｐ＝１００ａ＋１０ｂ＋ｃａ＋ｂ＋ｃ．（１）先固定ｂ，ｃ，则ｐ＝１００（ａ＋ｂ＋ｃ）－９０ｂ－９９ｃａ＋ｂ＋ｃ＝１００－９９ｂ＋９９ｃａ＋ｂ＋ｃ．因为ｂ，ｃ固定，所以ａ越小时，ｐ越小．所以当ａ＝１时，ｐ才可能取到最小值．（２）再固定ｃ，则ｐ＝１００＋１０ｂ＋ｃ１＋ｂ＋ｃ＝１０（ｂ＋ｃ＋１）－９ｃ＋９０１＋ｂ＋ｃ＝１０＋９０－９ｃ１＋ｂ＋ｃ．因为９０－９ｃ恒大于零，所以ｂ越大，ｐ越小．从而知当ｂ＝９时，ｐ才可能取到最小值．（３）ｐ＝１００＋９０＋ｃ１＋９＋ｃ＝ｃ＋１０＋１８０ｃ＋１０＝１＋１８０ｃ＋１０．因为ｃ越大，ｐ越小，所以当ｃ＝９时，ｐ才能取到最小值，故可知使ｐ取到最小值的三位数为１９９．同理，使ｐ取到最大值的三位数为９１１．１４．令ｔ＝２ｘ－ｘ槡２＝－（ｘ－１）２　＋槡１，０≤ｔ≤１，则ｙ＝３（ｘ２－２ｘ）＋２　２ｘ－ｘ槡２＋４＝－３ｔ　２＋２ｔ＋４＝－３　ｔ－１３（）２＋１３３，由０≤ｔ≤１，得３≤ｙ≤１３３．故ｙ的最大值和最小值分别为１３３和３．１５．作图可知△ＡＢＣ∽△Ａ′Ｂ′Ｃ′，且ＡＢＡ′Ｂ′＝１２，又由三角形相似性质，得·５４·Ｓ△Ａ′Ｂ′Ｃ′＝４Ｓ△ＡＢＣ＝２４．１６．由题意知ｘ２－（ｋ－１）ｘ＋（ｋ２＋３ｋ＋４）＝０有两实数根，所以Δ＝（ｋ－１）２－４（ｋ２＋３ｋ＋４）≥０，解得－３≤ｋ≤－５３．由韦达定理得ａ＋ｂ＝ｋ－１，ａｂ＝ｋ２＋３ｋ＋４，ａ２＋ｂ２＝（ａ＋ｂ）２－２ａｂ＝－ｋ２－８ｋ－７＝－（ｋ＋４）２＋９，由－３≤ｋ≤－５３，得ａ２＋ｂ２的最大值为８．１７．因为７８４÷５６＝１４，所以共可分成１４个班．又３００÷（１４×２）＝１０……２０，２０－１４＝６，１４－６＋１＝９，所以编号是３００号的同学应分在９班．１８．当直线与抛物线相切时，即ｘ２－ｘ－ｍ＝０有重根，可得ｍ＝－１４；当ｙ＝ｘ＋ｍ的图象分别过点（２，４）及点（０，０）时，它与ｙ＝ｘ２（－２≤ｘ≤２）的图象都恰有１个在ｙ轴右侧的交点，此时ｍ分别为０和２；当ｍ在区间（０，２）内变化时，也满足题意．所以ｍ的取值范围是［０，２］∪－１４｛｝．１９．ａｎ＝５９（１０ｎ－１）＋（ｎ－１）（ｎ－２）·（ｎ－３）．（答案不唯一）２０．将Ｍ中元素从小到大排列，若从第ｍ个与第ｍ＋１个数的位数没有增加，则第ｍ＋１个数的最高位必是９；反之，最高位是９的数与前一个数的位数一定相同，所以Ｍ中最高位是９的数共有２００６－１９１４＝９２（个）．三、解答题２１．（１）作ＤＥ⊥ＡＢ于Ｅ（如图７所示），图７则ＤＥ＝２ｓｉｎθ，ＡＥ＝２ｃｏｓθ，ＢＥ＝５－２ｃｏｓθ，ＢＤ＝ＤＥ２＋ＥＢ槡２＝４ｓｉｎ２θ＋２５－２０ｃｏｓθ＋４ｃｏｓ２槡θ＝２９－２０ｃｏｓ槡θ．（２）Ｓ１＝１２ＡＢ·ＤＥ＝５ｓｉｎθ，取ＢＤ中点Ｍ，连接ＣＭ（如图７所示），由ＤＣ＝ＣＢ，得ＣＭ⊥ＢＤ，ＣＭ２＝ＤＣ２－ＤＭ２＝４－１４（２９－２０ｃｏｓθ）＝５ｃｏｓθ－１３４，Ｓ２２＝１２ＢＤ·ＣＭ（）２＝１４（２９－２０ｃｏｓθ）５ｃｏｓθ－１３４（）＝－２５ｃｏｓ２θ＋１０５２ｃｏｓθ－３７７１６，于是ｆ（θ）＝Ｓ２１＋Ｓ２２＝２５ｓｉｎ２θ－２５ｃｏｓ２θ＋１０５２ｃｏｓθ－３７７１６＝－５０ｃｏｓ２θ＋１０５２ｃｏｓθ＋２３１６＝－５０ｃｏｓθ－２１４０（）２＋４８７３２．当Ｄ，Ｃ，Ｂ共线时，由余弦定理可得ｃｏｓθ＝１３２０；当Ａ，Ｄ，Ｃ共线时，同理可得ｃｏｓθ＝３７４０．因为ＡＢＣＤ是凸四边形，·６４·所以ｃｏｓθ的取值区间为１３２０，３７４０（）．令ｃｏｓθ＝ｔ，则ｆ（θ）＝－５０　ｔ－２１４０（）２＋４８７３２＝ｇ（ｔ）．因为ｔ∈１３２０，３７４０（），所以ｇ（ｔ）在１３２０，３７４０（）上单调递减，又ｇ１３２０（）＝２３１１６，ｇ３７４０（）＝２３１３２，所以ｆ（θ）的值域为２３１３２，２３１１６（）．２２．由题中给出的对应关系，有Ｖ，Ｗ，Ｘ，Ｙ，Ｚ∈｛０，１，２，３，４｝．由于三个递增的相邻的自然数被编成ＶＹＺ，ＶＹＸ，ＶＶＷ，所以２５Ｖ＋５Ｙ＋Ｚ＝２５Ｖ＋５Ｙ＋Ｘ－１，２５Ｖ＋５Ｙ＋Ｘ＝２５Ｖ＋５Ｖ＋Ｗ－１，烅烄烆即Ｚ＝Ｘ－１，５（Ｖ－Ｙ）＝Ｘ－Ｗ＋１．烅烄烆①②因为被编成ＶＹＸ，ＶＶＷ的十进制的自然数是递增的，所以Ｖ＞Ｙ．由②知５｜Ｘ－Ｗ＋１，且Ｘ－Ｗ＞０，所以Ｘ－Ｗ＋１＝５，Ｖ－Ｙ＝１，即Ｘ＝４＋Ｗ≥４，但Ｘ≤４，所以Ｘ＝４，Ｗ＝０，Ｚ＝３，于是Ｖ，Ｙ∈｛１，２｝，而Ｖ－Ｙ＝１，所以Ｖ＝２，Ｙ＝１．因此，ＶＷＸＹＺ所对应的十进制数是２×５４＋０×５３＋４×５２＋１×５＋３＝１３５８．２３．（１）即求ｙ＝ｘ２＋２ｘ＋１ｘ２＋ｘ＋１的值域，易得（ｘ２＋ｘ＋１）ｙ＝ｘ２＋２ｘ＋１，所以（ｙ－１）ｘ２＋（ｙ－２）ｘ＋（ｙ－１）＝０．当ｙ＝１时，－ｘ＝０，即ｘ＝０；当ｙ≠１时，Δ＝（ｙ－２）２－４（ｙ－１）２≥０，即ｙ（３ｙ－４）≤０，解得０≤ｙ≤４３．综上可知ｙ＝ｘ２＋２ｘ＋１ｘ２＋ｘ＋１的值域为０，４３［］．（２）由ｙ＝ｘ２＋ｋｘ＋１ｘ２＋ｘ＋１可得（ｘ２＋ｘ＋１）ｙ＝ｘ２＋ｋｘ＋１，即（ｙ－１）ｘ２＋（ｙ－ｋ）ｘ＋（ｙ－１）＝０．当ｋ＝１时，ｙ≡１，所以不存在灾数ａ，ｂ，ｃ使ｆ（ａ）＋ｆ（ｂ）＜ｆ（ｃ）；当ｋ≠１时，若ｙ＝１，则ｘ＝０；若ｙ≠１，则Δ＝（ｙ－ｋ）２－４（ｙ－１）２≥０，即３ｙ２＋（２ｋ－８）ｙ＋（４－ｋ２）≤０，解得４－ｋ－２｜ｋ－１｜３≤ｙ＜１或１＜ｙ≤４－ｋ＋２｜ｋ－１｜３．综上可知ｙ∈４－ｋ－２｜ｋ－１｜３，４－ｋ＋２｜ｋ－１｜３［］．假设对任意的实数ａ，ｂ，ｃ都有ｆ（ａ）＋ｆ（ｂ）≥ｆ（ｃ），则有２（４－ｋ－２｜ｋ－１｜）３≥４－ｋ＋２｜ｋ－１｜３，解得ｋ∈２５，１０７［］．所以若存在实数ａ，ｂ，ｃ使得ｆ（ａ）＋ｆ（ｂ）＜ｆ（ｃ），则ｋ∈－∞，２５（）∪１０７，＋∞（）．·７４·。

第17届全国希望杯数学竞赛试题高.doc

第十七届“希望杯”全国数学邀请赛高一第1试3月19日上午8:00至10：00一、选择题（每小题4分，共40分）以下每题的4个选项中仅有一个是题号 1 2 3 4 5 6 7 8 9 10 共得分答案１．设{(,)|0},{(,)|0,0},S x y xy T x y x y =>=>>则（）(A) S T S =U (B) S T T =U (C) S T S =I （D ）S T S =I２．若1()f x x=的定义域为A ，()(1)()g x f x f x =+-的定义域为B ，那么（）（A ）A B R =U (B) ＡＢ（Ｃ）A B ⊆ （Ｄ）A B =ΦI ３．已知tan 1,sin cos 0,()ααα>+<且则（A ）cos 0α> （Ｂ）cos 0α< （Ｃ）cos 0α= （D ）cos α的符号不确定４．设210,1,(),24x a a y a >≠=-若的反函数的图像经过点则()a =（Ａ）１６（Ｂ）４（Ｃ）２ 2５．已知0a ≠，函数32()f x ax bx cx d =+++的图像关于原点对称的充要条件是（）（Ａ）0b = （Ｂ）0c = （Ｃ）0d = （Ｄ）0b d ==６．若ABC V 三条边的长依次为33sin ,cos ,144a b c ===，则三内角Ａ，Ｂ，Ｃ的大小顺序为（）（Ａ）A B C << （Ｂ）B A C << （Ｃ）C B A << （Ｄ）C A B << ７．若实数x 满足2log 32cos ,|2||33|()x x x x =+-+-则等于（Ａ）352x - （Ｂ）３１（Ｃ）235x - （Ｄ）235x -或352x -８．区间[,0]:2m f x x m →+在映射所得的象集区间为[,]a b ，若区间[,]a b 的长度比区间 [0,]m 的长度大５，则m ＝（）（Ａ）５（Ｂ１０（Ｃ）２．５（Ｄ）１１０．函数22()962f x x ax a a =----在区间11[,]33-上的最大值为－３，则a 的值是（）（Ａ）32- 622或 6226-或（Ｄ）26-或-2。

2017浙江省高中数学竞赛试卷(PDF版)

5 q 6. 设 S 是 (0, ) 中所有有理数的集合，对简分数 ∈ S , ( p, q) = 1 ，定义函数 8 p 2 q q +1 ，则 f ( x) = 在 S 中根的个数为 _____________. f( )= 3 p p
解答由于 f ( x) =
2 2m − 1 5 1 m∈ ，，令 q = 2m − 1, p = 3m ，则有 0 < < ， <m<8 3 3m 8 2
x 2 + 32 > x 2 + 8 x 2 = 3 x （ 0 < x < 2 ）.
x2 + 16 f k ( x) > x 2 + 1 6 x > 3x 。 3
当 n = k 时，设 f k ( x) > 3 x ，则 f k +1 ( x) =
由此可得 0 < x < 2 都不是 f n ( x) = 3 x 的解（对于所有的 n）. 因此，对每个 n ， f n ( x) = 3 x 的实数解为 x = 2 。 …………………………20 分
有三个根 x1 < x2 < x3 . 若 x3 − x2= 2( x2 − x1 ) ，则实数 a = 解答：设 g ( = x) 2 1 − x 2 ，定义域为 −1 ≤ x ≤ 1 ，
max ( f ( x), g ( x)) = 1 ( f ( x) + g ( x) + f ( x) − g ( x) ) . 2
−4k 。 3k 2 + 1
……………………5 分
于是有 y p + yq= k ( x p + xq ) − 4k= 因为 PQ 的中点为 N ，所以 N (

历届(1-18届)希望杯数学邀请赛高二试题第二试(含答案WORD)(全国通用

第一届“希望杯”全国数学邀请赛(高二)第二试1990年4月15日上午8：30—10：30一、选择题1、直线A x + B y + C = 0（A ，B 不全为零）的倾斜角是（）（A ）B = 0时，倾斜角是2π，B ≠ 0时，倾斜角是arctan ( –A B )（B ）A = 0时，倾斜角是2π，A ≠ 0时，倾斜角是arctan ( –BA )（C ）A = 0时，倾斜角是0，A ≠ 0时，倾斜角是arctan ( –B A ) （D ）B = 0时，倾斜角是0，B ≠ 0时，倾斜角是arctan ( –AB)2、数列{ a n }：a 1 = p ，a n + 1 = q a n + r （p ，q ，r 是常数），则r = 0是数列{ a n }成等比数列的（）（A ）充分不必要条件（B ）必要不充分条件（C ）充要条件（D ）不充分也不必要条件 3、f 是R → R 上的一一映射，函数y = f ( x )严格递增，方程x = f ( x )的解集为P ，方程x = f [ f ( x )]的解集为Q ，则（）（A ）P ⊂ Q （B ）P = Q （C ）P ⊃ Q （D ）以上都不对4、点( x ，y )的坐标x ，y 都是有理数时，该点称为有理点，在半径为r ，圆心为( a ，b )的圆中，若a ∈Q ，b ∈Q ，则这个圆上的有理点的数目（）（A ）最多有一个（B ）最多有两个（C ）最多有三个（D ）可以有无穷多个5、以某些整数为元素的集合P 具有以下性质：（1）P 中元素有正数也有负数；（2）P 中元素有奇数也有偶数；（3）– 1 P ；（4）若x ，y ∈P ，则x + y ∈P 。

对于集合P ，可以断定（）（A ）0∈P ，2 P （B ）0 P ，2∈P （C ）0∈P ，2∈P （D ）0 P ，2 P 二、填空题6、方程arcsin ( sin x ×||x 的实根个数是。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2017年高中“希望杯”浙江省二试试题高一一、选择题：本大题共10个小题,每小题4分,共40分.1.已知锐角α终边上一点的坐标为(2sin 3,2cos3)-，则α=（） A ．3π- B ．3 C ．32π-D ．32π-2.若定义在R 上的函数(1)y f x =-是奇函数，则()f x 的图象一定过点（） A ．（0，0） B ．（1，0） C ．（-1，0） D ．（1，-1）3.在集合(0,1)(1,)+∞上定义运算“★”：{|l o g ,,}ax A A x b a b B =∈∈★B=，则集合11{,}2{2,4}4★的真子集的个数是（）A ．1B ．3C ．7D ．15 4.Two sets expressed asA=2{(,)|sin 1.2sin 1,}x y y x x x R =-+∈,B=sin {(,)|2,}xx y y x R -=∈then the number ofelement for AB is ( )A ．0B ．1 C.2 D ．infinite5.设32()366f x x x x =-+-，且()1,()5f a f b ==-，则a b += （） A ．-2 B ．0 C.1 D ．26.若0a ≠，则等比数列333248log 5,log 5,log 5a a a a a a ++++++的公比是（）A ．12 B ．2 C.13D ．3 7.`2()(1)()(0)31x F x f x x =-≠+是偶函数，且()f x 不恒等于0，则()f x （）A ．是奇函数B ．是偶函数 C.可能是奇函数，也可能是偶函数 D ．既不是奇函数，也不是偶函数8.对于方程||0x x px q ++=进行讨论，下面有四个结论：①至多有三个实根.②至少有一个实根.③仅当240p q -≥时才有实根.④当0p <和0q >时，有三个实根.A ．1个B ．2个 C.3个 D ．4个9.如图，在长方体1111ABCD A B C D -中，15,10,6AB AA AD ===，点E 在1DD 上，点F 在AD 上，点G 在AB 上，且1:1:2,:2:3,:3:4DF FA D E ED BG GA ===，则EFG ∆（图中阴影部分）在平面11BCC B 上正投影的面积是（）A ．8B ．10 C.12 D ．1510.设定义在R 上的函数()f x 满足3()()2f x f x =-+，又知(0)2,(1)2,(2)3f f f =-==，则(1)(2)(3)(2009)f f f f ++++的值等于（）A ．2009B ．2010 C.2011 D ．2012第Ⅱ卷（共90分）二、填空题（每题4分，满分40分）11.已知函数222,0,()2,0.x x x f x x x x ⎧--≥⎪=⎨-<⎪⎩若2(3)(2)f a f a ->，则实数a 取值范围是．12.设432()f x x ax bx cx d =++++，其中,,,a b c d 是常数，如果(1)10,(2)20,(3)30f f f ===，则(10)(6)f f +-= ．13.用[]x 表示不超过实数x 的最大整数，若0[sin(10)1k ⨯=-，则最小正整数k 为．14.若13(2)2()3(0)f x f x x x+=≠，则()f x = ．15.若(1sin )(1sin )y a x a x =++--，当1sin 0x +=时，y 取得最小值；当sin 0a x +=时，y 取得最大值，则a 的取值范围是．16.已知数列{}n a 满足*11210()n n n a a a n N ++++=∈110,n n a b a c==+，若{}n b 是等差数列，且其前n 项和为n S ，则2013S = ．17.不等式组424222log (824)33sin cos 2y y x x x y ππ-+⎧-+≤⎪⎨≥⎪⎩的解集是．18.If a sequence {}n a is definde as 1125,21n n a a a n +=-=-,then the minimum value ofna nis ． 19.已知函数()(*),f n k n N k =∈是0.9196461178┅ 的小数点后的第n 个数字，则5(((5)))8(((8)))f f f f f f += ．20.设:p 函数()log(101)xf x ax =+-是偶函数，:q 函数42()2x xag x -=是奇函数，则p 是q 的条件（填必要不充分，或充分不必要，或充要，或既不充分也不必要）．三、解答题每题都要写出推算过程.21. 已知数列}{n a ，其中.2,3211n n n a a a a +==+ （1）求}{n a 的通项公式；（2）求满足20121>n a 的n 的最小值.22.在ABC ∆中，c b a ,,分别是角C B A ,,所对的边，已知5,8==c b ，且)sin sin )(sin (C B A c b a -+++ .sin )32(B a +=（1）求角C 的大小；（2）求.ABC S ∆23.已知函数⎪⎩⎪⎨⎧<-≥+=.0),1(log ,0),1(log )(212x x x x x f（1）判断函数)(x f y =的奇偶性；（2）对任意两个实数21,x x ，求证：当021>+x x 时，0)()(21>+x f x f ；（3）对任何实数0)23()(,2≥-+-x xe f a ef x 恒成立，求实数a 的取值范围.试卷答案一、选择题1-5: CCCDD 6-10:CABCD二、填空题11. 31<<-a 12.8104 13. 19 14.xx 56109-15.[－1，0]16. 2027091 17.)}1,2)(1,2(|),{(---y x 18.54119.8620.充要三、解答题21.（1）由n n n a a a 221+=+，得21)1(1+=++n n a a由题设，易知 0>n a于是2212)1(log )1(log +=++n n a a即)1(log 2)1(log 212+=++n n a a所以)}1({log 12++n a 是以2)13(log 2=+为首项，2为公比的等比数列故nn n a 222)1(log 12=⋅=+-则nn a 221=+ 因此122-=nn a (2)由20121>n a ，即20121122>-n，得2012222>n因为1514221638420122163842=⨯<<=，所以*,22142N n n∈> 即152,22152≥≥n n故4≥n . 因此，所示n 的最小值是22.解：由)sin sin )(sin (C B A c b a -+++.sin )32(B a +=及正弦定理，可得()()(2a b c a b c ab +++-=即2222(2a ab b c ab ++-=+222c a b =+由余弦定理，可得6C π=或56π，因为b c >，所以于是，当56C π=时，B 也是钝角，不满足三角形内角和定理，故 6C π=.(2)图中,ABC ∆可以是锐角三角形，也可以是钝角三角形.从A 作AD BC ⊥于D ，则在Rt ADC ∆中，14,22AD AC DC AC ====又3BD =，所以3BC =+或3BC =-+故162ABC S BC AD ∆=⋅=±+ 23.（1）因为2(0)log (10)0f =+=当0x <时，0x ->，所以12()log (1)f x x =-2log (1)x =--()f x =-即()()f x f x -=-当0x >时，0x -<，所以12()log [1()]f x x =--2log (1)x =-+()f x =-即()()f x f x -=-综上知，()y f x =是奇函数.(2)因为2log y x =是单调递增函数，1u x =+也是单调递增函数，由复合函数的单调性知当0x ≥时，2log (1)y x =+是单调递增函数由（1）知由奇函数的单调性，知0x <时，()f x 是单调递增函数从而()y f x =是定义在R 单调递增上的奇函数，由021>+x x ，得，12x x >- 所以122()()()f x f x f x >-=- 即0)()(21>+x f x f (3)因为2()(32)0xx f e a f e -+-≥所以2()(32)(23)xx x f e a f e f e -≥--=-于是223xx ea e -≥-即2223(1)2xx x a ee e ≥-+=-+当0x =时，2(1)2xe -+有最小值2, 所以只需2a ≤，就有2()(32)0xx f ea f e -+-≥恒成立，故a 的取值范围是(,2]-∞.。