半波损失
半波损失
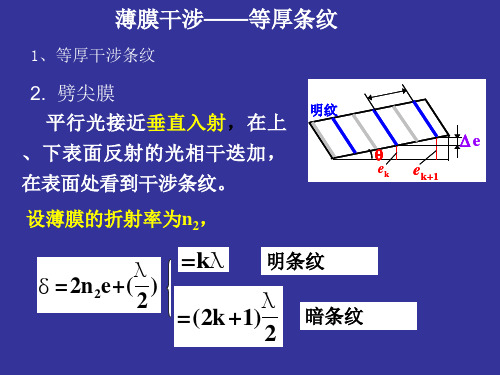
而激光器两端装有反射镜。就镀有增反(射)膜。
1.增透膜 光学镜头为减少反射光, 通常要镀增透膜。
增透膜是使膜上下两表面 的反射光满足减弱条件。
2n2 d cos r (2k 1) 2 2
(k 1,2)
减弱
例:为增强照相机镜头的透射光,往往在镜头 (n3=1.52)上镀一层 MgF2 薄膜(n2=1.38),使对人 眼和感光底片最敏感的黄绿光 = 555 nm 反射最小, 假设光垂直照射镜头,求:MgF2 薄膜的最小厚度。 解: n1
9
3 10 m
7
在该厚度下蓝紫光反射加强,所以我们看到镜头表面 为蓝紫色。 2.增反膜
减少透光量,增加反射光,使膜上下两表面的反射光满 足加强条件。 例如:激光器谐振腔反射镜采用优质增反膜介质薄膜 层已达15 层,其反射率99.9%。
e处 0为暗
明纹
暗纹
L
劈棱 e L sin ek 1 ek 2n 2 ek ek+1 L ≈ (适于平行光垂直入射) 2n 2 sin 2n 2
很小的劈尖上,才能看到干涉条纹 只有在
(4) 当某种原因引起膜的等厚线发生变化时,将 引起条纹作相应地移动。
2 2 2 r 2 e R e R e e 所以 k k k ,由于 k , k 可忽略,
R 2 ( R ek ) 2 rk2
因此得到:
r ek 2R
2 k
(此式说明: k 与 rk 成正比,即离开中心愈 远,光程差增加愈快,因此,干涉环愈密。)ຫໍສະໝຸດ e2整理后得:
r R k
2. 环数不可数错,在数的过程中发现环数有变化时,必须重测。 3. 测量中,应保持桌面稳定,不受振动,不得触动牛顿环装置, 否则重测。
半波损失的概念

半波损失的概念
1. 半波损失是一个概率统计的概念,用来描述在赌球、投注等活动中可能会出现的输赢情况。
2. 它指的是在某一场比赛中,赌徒如果投注了半球、一球、球半,而这场比赛的胜负结果是平局或是主队(客队)只赢一个球,这时该赌徒将会损失一半(或部分)的投注金额。
3. 这种损失是由于投注者在下注时没有完全预测到比赛的结果,导致了失误,从
而带来了不必要的损失。
4. 半波损失并不是一种避免不了的损失,因为投注者可以通过更加准确地预测比赛结果来减少这种损失,或者通过合理的投注策略来控制损失程度。
5. 在体育竞猜中,半波损失是一个普遍存在的问题,因为投注者需要考虑许多因素,如球队实力、比赛场地、伤病情况等等,才能做出最好的投注决策。
6. 因此,投注者需要在投注前进行充分的研究和分析,以便减少半波损失的可能性,同时还要遵守投注的原则和规则,不盲目追逐高赔率、不超出自己的承受能力等等。
7. 正确理解和应对半波损失的概念和影响,可以帮助投注者保持冷静和理性,提高投注的准确性和稳定性,从而取得更多的收益。
半波损失的条件

目录半波损失定义半波损失理论的应用半波损失的原因定义光从光疏介质射向光密介质时反射过程中,如果反射光在离开反射点时的振动方向相对于入射光到达入射点时的振动方向恰好相反,这种现象叫做半波损失。
从波动理论知道,波的振动方向相反相当于波多走(或少走)了半个波长的光程。
入射光在光疏媒质中前进,遇到光密媒质界面时,在掠射或垂直入射2种情况下,在反射过程中产生半波损失,这只是对光的电场强度矢量的振动而言。
如果入射光在光密媒质中前进,遇到光疏媒质的界面时,不产生半波损失。
不论是掠射或垂直入射,折射光的振动方向相对于入射光的振动方向,永远不发生半波损失。
光的干涉现象是有关光的现象中的很重要的一部分,而只要涉及到光的干涉现象,半波损失就是一个不得不考虑的问题。
光在不同介质表面反射时,在入射点处,反射光相对于入射光来说,可能存在半波损失,半波损失可以通过直观的实验现象——干涉花样——来得到验证。
半波损失理论的应用半波损失理论在实践生活中有很重要的应用,如:检查光学元件的表面,光学元件的表面镀膜、测量长度的微小变化以及在工程技术方面有广泛的应用。
半波损失的原因在洛埃镜实验中,如果将屏幕挪进与洛埃镜相接触。
接触处两束相干波的波程差为零,但实验发现接触处不是明条纹,而是暗条纹。
这一事实说明洛埃镜实验中,光线自空气射向平面镜并在平面镜上反射后有了量值为∏的位相突变,这也相当于光程差突变了半个波长。
光在反射时为什么会产生半波损失呢?这是和光的电磁本性有关的,可通过菲涅耳公式来解释。
在任何时刻,我们都可以把入射波、反射波和折射波的电矢量分成两个分量,一个平行入射面,另一个垂直入射面。
有关各量的平行分量和垂直分量依次用指标p和s表示。
以i1、i1´ 和i2分别表示入射角、反射角和折射角,它们确定了各波的传播方向。
以A1、A1´、A2来依次表示入射波、反射波和折射波的电矢量的振幅,它们的分量相应就是Ap1、Ap1´、Ap2和As1、As1´、As2。
半波损失的原理以及应用

半波损失的原理以及应用原理介绍半波损失是指电信号在传输过程中由于阻抗不匹配而发生一部分的信号损失的现象。
在电路传输中,当电信号穿过不同阻抗的界面时,会发生反射和透射。
如果传输线的特性阻抗与负载的阻抗不匹配,会导致反射波的产生。
在传输线上反射波的传输,会导致信号损失。
这种损失被称为半波损失。
半波损失可以通过匹配传输线阻抗和负载阻抗来减轻。
通过调整传输线的特性阻抗,使之与负载的阻抗相匹配,可以最大限度地减少反射波的产生,从而降低半波损失。
应用半波损失的原理在电子领域有广泛的应用,以下是一些常见的应用场景:1.电路设计中的阻抗匹配:在设计电路时,为了减小半波损失,需要对传输线的特性阻抗和负载阻抗进行匹配。
例如,在高频电路中,使用阻抗匹配网络来确保信号的正常传输。
2.无线通信中的天线设计:在无线通信系统中,天线是信号的传输和接收的重要部分。
为了减小半波损失,天线的输入阻抗应该与无线电接收机或发射机的输出阻抗相匹配。
这可以通过调整天线结构和使用匹配网络来实现。
3.光纤通信中的信号传输:在光纤通信系统中,信号的传输通过光纤进行。
由于光纤的特性阻抗与连接器等的阻抗不匹配,会导致反射波的发生,进而导致半波损失。
为了减小损失,光纤连接器的设计中需要特别注意阻抗匹配。
4.音频设备中的信号传输:在音频设备中,如音响系统、录音设备等,信号的传输也会受到半波损失的影响。
为了保证音频信号的质量,需要在信号线和设备之间进行阻抗匹配。
如何减小半波损失要减小半波损失,可以采取以下措施:1.阻抗匹配:通过调整传输线的特性阻抗和负载的阻抗,使之相匹配,减小反射波的产生,从而降低半波损失。
2.使用匹配网络:在阻抗不匹配的情况下,可以使用匹配网络来确保信号的正常传输。
匹配网络中的元件可以根据需要调整阻抗,使其与传输线的特性阻抗和负载阻抗相匹配。
3.优化传输线的设计:传输线的设计也对减小半波损失起到重要作用。
合理选择传输线的材料、几何尺寸和布线方式等,可以降低传输线的特性阻抗与负载阻抗之间的差异,减小反射波的发生。
半波损失

什么是半波损失(What) 为什么会出现半波损失(Why) 出现了半波损失怎么办(How)
What
定义:当波动(含光波)从波疏介质向波密介质正入射或
者掠入பைடு நூலகம்时,反射光与入射光相比有π的相位跃变(或等效
于半个波长)的现象。
说明:
1、透射波动总无半波损失; 2、波动如果是从波密介质到波疏介质入射,无半波损失; 3、如果入射角不是接近于0°或90 ° ,实际情况复杂,应 由菲涅尔公式表征。但大学物理中如有出现,亦不区分入 射角情况。
Why
半波损失出现与否,由边界条件决定。从本质上说,
是能量守恒和动量守恒的必然要求。
1、机械波 如果反射点为固定端,相当于波阻无限大,波动无法进 入第二介质传播,即第二介质为波密介质。 由于反射点固定,必然要求入射波和反射波在该反射点 相位相反,相当于波程的半个波长。
2、光波 两次反射波表象光程差:
n1 n2 n1
h
L 2n2 h
如果ΔL=(k+1/2)λ,或者说反
射光干涉相消。
而:两次透射波表象光程差亦是,即也是ΔL干涉干涉相消, 明显不符合能量守恒条件。 当其中有个出现半波损失时,恰好符合。
How
1、总光程差等于表象光程差加上附加光程差。
Δ= Δ0+ Δ’
考虑到最后实际对干涉起决定作用的是相位差和余弦函数 的周期性,整个干涉光路出现奇数次半波损失时,附加光 程差取±λ/2 ,而偶数次时取零。 2、附加光程差不等于零时,对条纹的影响仅仅是“颠倒黑 白”,而不会改变条纹的形状、间距、对比度等性质。
解释半波损失概念

半波损失解析:电路中能量损失的原因与影响半波损失是指在电路中由于负载或其他因素引起的能量损失,该损失发生在每个电流周期的一半波形中。
在交流电路中,电流和电压是周期性变化的,而半波损失是指在每个周期中,只有电流或电压的一半波形能够有效地传递能量,另一半波形则产生能量损失。
半波损失主要发生在具有非线性特性的元件或负载上。
在这些元件或负载中,电流和电压的波形不完全对称,导致一部分能量无法有效地传输或被利用。
这些非线性元件或负载可能导致能量的转换效率降低,并且产生额外的热量和能量损失。
半波损失的存在对电路性能和能源利用效率具有影响。
为了减少半波损失,可以采取一些措施,例如使用更高效的元件和电路设计,优化负载匹配,降低电路的损耗和不对称性等。
总之,半波损失是指在交流电路中由于非线性元件或负载的存在,导致每个周期中只有电流或电压的一半波形能够有效地传递能量,而另一半波形产生能量损失。
通过优化电路设计和采用高效的元件,可以减少半波损失,提高能源利用效率。
光的半波损失原理的解释

光的半波损失原理的解释光的半波损失(Half-Wave Loss)通常是在光学系统中讨论的一个概念,主要涉及到光波的反射和传输过程中的相位差问题。
这一概念涉及到光波的干涉和相位差的概念。
基本原理解释:1.相位差:光波在介质之间反射或透射时,由于折射率的不同,可能引起相位差。
相位差是波峰或波谷之间的相对位移,通常以波长(λ)的倍数来表示。
2.半波损失:当光波从一个介质传播到另一个介质时,如果反射界面的折射率差刚好是波长的一半(λ/2)或其整数倍,就会发生半波损失。
在这种情况下,反射波与透射波的相位差是λ/2,导致它们在某些方向上相互抵消,形成波的干涉,造成反射波减弱或完全抵消。
3.反射和透射:当光波从一个介质射向另一个介质时,一部分光波会反射回原来的介质,而另一部分会透射到新的介质。
这两部分光波的相位差决定了它们的叠加效果。
4.最小反射和最大透射:当反射波和透射波相互干涉时,如果相位差为λ/2或其整数倍,就会出现最小反射。
如果相位差为奇数倍的λ/4,则会出现最大透射。
这是典型的半波损失情况。
应用和注意事项:•薄膜涂层:半波损失原理在光学涂层设计中是一个关键的概念。
通过合理设计涂层的厚度和折射率,可以最小化反射,提高光学元件的透明性。
•多层膜:多层膜的设计可以利用半波损失原理,使得多层膜的反射率在某个波长范围内趋近于零。
•注意相位差:在设计光学系统时,特别是涉及到多个光学元件的系统中,需要注意光波的相位差,以避免意外的干涉效应。
总体而言,半波损失原理是光学设计和涂层技术中的一个基本概念,通过理解和合理利用这一原理,可以优化光学系统的性能。
菲涅尔公式和半波损失

菲涅尔公式和半波损失
菲涅尔公式是描述光在介质界面反射和折射的规律的公式。
它由法国物理学家菲涅尔在19世纪提出,包含了入射光线的入射角、介质的折射率以及反射和折射光线的角度关系等参数。
菲涅尔公式在光学中应用广泛,例如在光学薄膜和光学器件设计中的折射率匹配问题中。
半波损失是指在光学器件中,由于反射和透射的光线路程不同,导致传输的光强度降低一半的现象。
这个现象在光学通信和激光器中尤为常见。
减小半波损失是提高光学器件性能的重要方法之一,可以通过优化光学器件的设计、材料选择和制作工艺等方式实现。
因此,熟悉菲涅尔公式和半波损失的原理和应用,对于光学学科的研究和应用都具有重要的意义。
- 1 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§12.2分振幅的干涉(一) 薄膜反射光的干涉如(图12.2a ),一束平面光在透明薄膜上下两表面反射成两束光,让它们叠加在一起(例如用透镜会聚在一起)时,可满足相干条件。
它们的光程差L ∆可计算如下:()AE n BC AB n L 12-+=∆321n n n <<或321n n n >> (12.2.1)()212λ+-+=∆AE n BC AB n L 321n n n ><或321n n n <> (12.2.2)半波损失的情况比较复杂,本教材只按正入射和掠入射的情况列式1[1]。
如果折射率321n n n <<,则薄膜上下两表面的反射光都有半波损失;如果折射率321n n n >>,则上下两表面的反射光都没有半波损失。
因此,在(12.2.1)式中对这两种情况计算光程差时,都不计半波损失。
如果折射率321n n n ><或321n n n <>,则薄膜上下表面的两反射光中,一个有半波损失,另一个没有半波损失。
因此,在(12.2.2)式中计算这两种情况的光程差时,都应计算半波损失。
在(图12.2a )中,入射光对上表面的入射角与折射角为i 与r 。
由于C 与A 两点很靠近,此处薄膜上下表面可近似看成是平行的,因此,此光束对下表面的入射角可用r 表示。
设此处的薄膜厚度为e ,则可用e 、i 、r 诸量表示(12.2.1)式的光程差L ∆。
计算如下:r e BC AB cos ==,etgr AC 2=,i etgr i AC AE sin 2sin ==。
∴ ()i r n n r e i e t g r n r e n L s i n s i n c o s 2s i n 2c o s 22212-=-=∆。
将折射定律表式r n i n sin sin 21=代入上式,消去i sin 或r cos 得:()r en r n n r e L cos 2sin cos 22212=-=∆ (12.2.3) i n n r n n r n r n 2212222222222sin sin sin 1cos -=-=-= (12.2.4)将(12.2.3)式代入(12.2.1)及(12.2.2)式,并参考(12.1.18)式,可写出薄膜干涉(12.2.5) (12.2.6) 由于薄膜厚度e 不为负值或零,故k 与k '1[1] 赵凯华、钟锡华《光学》上册256页,1984年版。
(12.2.5) (12.2.5) (图12.2a 薄膜反射光的干涉)薄膜反射光的各级干涉极大条件薄膜反射形成干涉现象,是利用薄膜上下表面的反射,使一束光分成相干的两束光,也就是从一束光的强度中,分出两部分,经过略有不同的光程后叠加在一起,形成两束相干光。
由于光强度与振幅的平方成正比,所以这种从普通光源获得相干光的方法,称为分振幅的方法。
这与前一节所述分波阵面的干涉有些不同,计算光程差L ∆的公式也不同。
(二) 薄膜等厚干涉条纹的正入射观测法在薄膜干涉公式(12.2.5)和(12.2.6)中,薄膜的折射率2n 通常是常量,而厚度e 、折射角r 和波长λ可为变量。
对于厚度e 不均匀的薄膜,可用单色光按固定方向照射在薄膜上,观测其反射光的干涉条纹。
由于2n 、λ和r 都是常量,从(12.2.5)或(12.2.6)式可确定 ,3,2,1=k 各级干涉亮纹的厚度 ,,,321e e e 。
薄膜的同一级亮纹中各点的厚度都相等,不同级亮纹中各点的厚度不相等。
这种干涉条纹称为等厚干涉条纹。
它显示出上述薄膜的等厚线,从等厚干涉条纹可看出此薄膜的厚度分布情况。
观测薄膜的等厚干涉条纹,常采用正入射方法,即令入射角0=i ,折射角0=r ,则1c o s =r ,使干涉公式(12.2.5)及(12.2.6)得到简化。
正入射观测法的装置示意图,如(图12.2b )所示。
单色光源ξ放在透镜1τ的前焦点,ξ发出的光经透镜形成一束平行光,沿水平方向投射于倾角为 45的玻璃平板G (亦称分束器)。
一部分入射光透过玻璃板,另一部分入射光被玻璃板向下反射到达待测的薄膜MN ,此薄膜的上下表面将上述正入射的光、反射成两束相干光。
这两束相干反射光向上射到玻璃板G ,其中一部分相干光透过玻璃板向上到达观测的仪器(例如显微镜)E 中。
(三) 劈尖的干涉条纹(等厚干涉条纹的例子)如(图12.2c )将两片平板玻璃叠在一起,并在Q端夹进去一条纸(或一根金属丝,或一根头发丝),使这两片玻璃中间形成一个劈尖形状的空气薄膜。
在Q端是此空气劈尖的最厚处,在另一端P 是两玻璃片紧密接触处,也就是此空气劈尖的棱,此棱是一条垂直于图面的直线。
将上述两玻璃片以及其中间的空气劈尖PQ 放在(图12.2b )的MN 位置,便可从上方观测此空气劈尖上下两表面的反射光形成的等厚干涉条纹。
现在先说明一下,上述两片玻璃共有四个表面,为什么不讲最上表面与最下表面的反射光?这个道理可用我们家里的玻璃窗加以说明。
玻璃窗的玻璃的厚度约为3=r 毫米,一束入射光被它的前后两表面反射成两束光,其光程差L ∆约为:33100.91035.122--⨯=⨯⨯⨯==∆nr L 米。
如果用黄绿光在真空中波长55.0=λ微米,代表空气中可见光波长,则上述光程差L ∆相当于k 个波长,即4631064.11055.0100.9⨯=⨯⨯=∆=--λL k 个。
这表明一束光进入玻璃窗的后表面,并反射出第一个光波时,此玻璃的前表面已经反射出一万六千多个光波。
玻璃前后表面的两束反射光的光程差L ∆这么大,它们不会满足相干(图12.1b )等厚干涉条纹的正入射观测法(图12.2c )空气劈尖的等厚干涉条纹条件,2[2]我们在玻璃窗没看到干涉条纹。
同样道理,在(图12.2c )中用普通光源观测空气劈尖的干涉条纹时,由于空气劈尖不超过一张纸的厚度(远远小于1毫米),劈尖两表面的反射光会产生干涉条纹,而两片玻璃的最上与最下表面的反射光不会产生干涉条纹。
由于两玻璃片的折射率1n 与3n 都大于空气劈尖的折射率12=n ,故可参照(12.2.6)式 (12.2.7) k 换成半整数 ,5.1,5.0='k 便可确定其暗纹位置。
将0=e 代入上式可得5.0='k ,这表明劈尖棱0=e 应是第一级暗纹5.0='k 的位置。
这与实验观察结果相符,这结果也证明(12.2.6)式对反射光半波损失的分析与实验相符。
如(图12.2c ),空气劈尖的棱角α很小,为了便于作图讨论,将劈尖放大画在(图12.2d )中。
一束单色光正入射于劈尖上时,可形成一组与棱平行的、等距离的、亮暗相间的直线形等厚干涉条纹。
设相邻两亮纹(或相邻两暗纹)的间距为x ∆,厚度差为e ∆,则从(12.2.7)式可求得e ∆与x ∆的关系如下:(12.2.8) (12.2.9)如果两玻璃片中间不是空气劈尖而是液休劈尖;或是只用一薄片透明固体磨成固体劈尖,都可参照上述公式进行分析计算,但要注意12≠n ,并要根据折射率1n 、2n 、3n 的大小,决定选用(12.2.5)式或(12.2.6)式。
关于劈尖等厚干涉条纹的计算和实际应用,可参阅[例题12.2A]以及有关习题。
(四) 牛顿环(等厚干涉条纹的例子)如(图12.2e ),将一个曲率半径R 很大的平凸透镜的球形凸面、放在一个平板玻璃上,在透镜与玻璃板中间形成一个空气薄膜。
将此玻璃板与透镜放在(图12.2b )的MN 位置,便可看到此空气薄膜的同轴圆形等厚干涉条纹。
牛顿首先观察并描述这类条纹,故称之为牛顿环,或牛顿圈。
牛顿环可参照劈尖的干涉公式,只是几何关系式(12.2.9)不可用于牛顿环,因为,上述劈尖的干涉条纹是一组平行直线,而牛顿环则是一组圆环。
如(图12.2.e ),设某一级牛顿环的半径为ρ,对应的空气薄膜厚度为e ,则R 、ρ与()e R -三边组成一个直角三角形,其几何关系如(12.2.10)式所示。
此式代入(12.2.7)式便可得到牛顿环的干涉公式(12.2.11)。
()2222Re 2e e R R -=--=ρ。
程守洙、江之永主编《普通物理学》第三册(第三版)180—182,1979年版。
,(12.2.7) (12.2.8) (12.2.9) e R >>,Re 22=ρ λλρλk R n e n L =+=+=∆222222,3,2,1=k正入射空气劈尖,等厚亮纹条件 (图12.2.d )正入射劈尖等厚条纹的x ∆与e ∆ 射空尖等纹的e ∆(图12.2.e )牛顿环射牛各级(12.2.10)(12.2.11)将上式的整数k 换成半整数 ,5.1,5.0='k 便可得到各暗环的条件。
牛顿环的计算和应用可参阅[例题12.2B]及有关习题。
(五) 薄膜透射光的干涉与增透膜如示意图(图12.2a )及(图12.2f )所示,一束光在透明薄膜上下表面形成反射相干光a 与b 时,还会形成透射相干光a 1与b 1。
这两束透射光a 1与b 1的光程差()BF n CD BC n 12-+与(12.2.1)式所示反射光a 与b 的光程差()AE n BC AB n 12-+相等,但是,它们的半波损失情况肯定不同。
以空气中薄膜为例,321n n n ><,光束a 在A 点反射时有半波损失,光束b 在B 点反射时无半波损失,因此,a 与b 的光程差中应计入半波损失,如(12.2.2)式所示。
但是,透射光a 1无半波损失,透射光b 1在B 与C 两点反射时都无半波损失,因此,a 1与b 1的光程差不应计入半波损失。
从上述分析可知,反射光a 与b 形成干涉极大,显示反射亮纹时;透射光a 1与b 1就会形成干涉极小,显出透射暗纹。
反之,当a 与b 形成干涉暗纹时;a 1与b 1必形成干涉亮纹。
这个结论符合能量守恒定律的要求:薄膜反射一束光的强度多,则透射的强度少;反之若反射的强度少,则透射的强度多。
因此,只要将(12.2.1)与(12.2.2)式中的半波损失条件对换一下,或将亮纹与暗纹的条件对换一下,便可得到薄膜透射光的干涉公式。
如(图12.2g ),设在玻璃片(折射率52.13=n )上表面镀一层氟化镁(38.12=n )薄膜。
当波长为550=λ纳米的平行光,在空气中垂直入射于此薄膜时,如果要求达到此薄膜的反射极小,透射极大的效果。
可按照已知条件321n n n <<,将(12.2.5)式的整数k 改用半整数k ′,即可求得此氟化镁薄膜的厚度e 应约等于下列数值之一:500,300,100=e 纳米。
