矩阵范数详解.pdf
矩阵的范数和条件数

① A0,& A ,0 A0
② A A,R
③ A B A B, A ,B R n n ④ A B A B, A ,B R n n
⑤ Ax Ax, xRn
上海理工大学 理学院
University of Shanghai for Science and Technology
2 2 x x 1 1 6 .0 0 0 0 6 1 x x 2 2 8 8 .0 0 0 0 1 与 2 2 x x 1 1 5 .9 9 9 9 6 9 x x 2 2 8 8 .0 0 0 0 2
其解分别为:x
x1 x2
College of SciA的实值函数N(A)=‖A‖,满足条件:
(1)非负性: ‖A‖0 ,且‖A‖=0当且仅当 A=0; (2)齐次性: ‖A‖=| |‖A‖, R; (3)三角不等式:‖A+B‖‖A‖+‖B‖; (4)柯西-施瓦茨不等式:‖AB‖‖A‖‖B‖. 则称‖A‖为矩阵A的范数.
x
b
上海理工大学 理学院
University of Shanghai for Science and Technology
College of Science
注:一般判断矩阵是否病态,并不计算A1,而由经验得出。
行列式很大或很小(如某些行、列近似相关); 元素间相差大数量级,且无规则; 主元消去过程中出现小主元; 特征值相差大数量级。
A1
很小
A
A
A
A
条件数表示了对误差的放大率
上海理工大学 理学院
University of Shanghai for Science and Technology
矩阵范数

二、向量范数的抽象定义: 1、向量范数的定义 n n x 定义9(向量范数)对于向量 R 或x C 的某个实值非负
2、常用的向量范数 T n n x y x y 定义10 设x ( x1 ,, xn ) R (或x C ) N (1)向量的“∞”范数: ( x ) || x || max x i ; 1 i n
§9 向量,矩阵范数,矩阵的条件数 T 线性方程组,解的形式均为向量,如近似解 x x1 , x 2 ,, x n ,
该近似解的误差估计如何? 下一章要讨论解大型稀疏线性方程组的迭代法,迭代法的收 敛性怎样? 需要对向量空间R n 或矩阵空间 nn 的元素 “大小”给出某 R 度量。即向量范数(或矩阵范数)概念, 种 从而引进 n 或R nn中元素 R 的距离概念。 向量、矩阵与线性方程组有着密切的关系,向量、矩阵范数是 解方程组以及研究与探讨方程组本身性质的工具。 9.1 向量,矩阵范数 二维,三维的长度概念:
k k
max x
1 i n
(k ) i
(k ) x i 0(当k ) x x
k
0(当k )。
由范数的等价性定理有:
(k ) lim x x k (k ) lim x x
k
(k ) x x 0当k , (k ) 2 x x 0当k 。
T
2 2 R 2中,x R 2, x1 x2,其中x x1 , x2 ; x T 2 2 2 R 3中, x R 3, x 1 x 2 x 3 , 其中x x1 , x 2 , x 3 。 x 2 2 2 n x R n , x x1 x 2 x n , 其中x x1 , x 2 , , x n T 。 推广到 R :
矩阵范数标准详解

矩阵范数标准详解(总9页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--《周国标师生交流讲席010》向量和矩阵的范数的若干难点导引(二)一. 矩阵范数的定义引入矩阵范数的原因与向量范数的理由是相似的,在许多场合需要“测量”矩阵的“大小”,比如矩阵序列的收敛,解线性方程组时的误差分析等,具体的情况在这里不再复述。
最容易想到的矩阵范数,是把矩阵m n A C ⨯∈可以视为一个mn 维的向量(采用所谓“拉直”的变换),所以,直观上可用mn C 上的向量范数来作为m n A C ⨯∈的矩阵范数。
比如在1l -范数意义下,111||||||mnij i j A a ===∑∑()12tr()HA A =; ()在2l -范数意义下,12211||||||mnF ij i j A a ==⎛⎫= ⎪⎝⎭∑∑, ()注意这里为了避免与以后的记号混淆,下标用“F ”,这样一个矩阵范数,称为Frobenius 范数,或F-范数。
可以验证它们都满足向量范数的3个条件。
那么是否矩阵范数就这样解决了因为数学上的任一定义都要与其对象的运算联系起来,矩阵之间有乘法运算,它在定义范数时应予以体现,也即估计AB 的“大小”相对于A B 与的“大小”关系。
定义1 设m n A C ⨯∈,对每一个A ,如果对应着一个实函数()N A ,记为||||A ,它满足以下条件:(1)非负性:||||0A ≥;(1a )正定性:||||0m n A O A ⨯=⇔=(2)齐次性:||||||||||,A A C ααα=∈;(3)三角不等式:||A ||||||||||||,m n A B A B B C ⨯+≤+∀∈则称()||||N A A =为A 的广义矩阵范数。
进一步,若对,,m n n l m l C C C ⨯⨯⨯上的同类广义矩阵范数||||•,有(4)(矩阵相乘的)相容性:||A ||||||||||||AB A B ≤, n l B C ⨯∈, 则称()||||N A A =为A 的矩阵范数。
2.2矩阵的范数

§2.2 矩阵的范数我们知道:向量本身可以看作是矩阵,而一般的矩阵又有自身的运算特点,比如矩阵的乘法运算。
因此,我们定义矩阵的范数时需要考虑矩阵的本身的特点,这就有了我们以下要讨论的内容:一、 矩阵的范数1.矩阵范数的定义设||||:m n C R ×→i 是实值函数,若它满足下述三个条件: (1) 非负性:,||||0,and ||||00m n A C A A A ×∀∈≥=⇔= (2) 齐次性:,,||||||||||m n k C A C kA k A ×∀∈∈= (3) 三角不等式:,,||||||||||||m n A B C A B A B ×∀∈+≤+ 则称||||i 为广义矩阵范数,若||||i 还满足下述第四个性质: (4) 相容性:,,||||||||||||m n n l A C B C AB A B ××∀∈∈≤i 则称||||i 为矩阵范数。
注:在相容性的定义中,n l B C ×∈,m l AB C ×∈,实数||||B ,||||AB 的定义规则与实数||||A 的定义规则相同。
2. 矩阵范数的连续性与向量的情况一样,对于矩阵序列而言,它也有极限的概念。
设矩阵序列(){}k A ,其中()k m n A C ×∈,若()k A 的每一个元素()k ij a 均有极限ij a ,则称矩阵序列(){}k A 有极限()ij A a =,或者说(){}k A 收敛到矩阵A ,记作()()lim ()k k k A A A A →+∞=→不收敛的矩阵序列称为发散的。
当然,也可按照范数定义矩阵的收敛性。
即若()lim 0k k A A →∞−=则称(){}k A 在范数||||i 意义下收敛于A 。
由三角不等式,可推知,,m n A B C ×∀∈有||||||||||||||A B A B −≥−。
矩阵范数详解.docx

《周国标师生交流讲席010》向量和矩阵的范数的若干难点导引(二)一.矩阵范数的定义引入矩阵范数的原因与向量范数的理由是相似的,在许多场合需要“测量”矩阵的“大小”,比如矩阵序列的收敛,解线性方程组时的误差分析等,具体的情况在这里不再复述。
最容易想到的矩阵范数,是把矩阵A C m n可以视为一个mn维的向量(采用所谓“拉直”的变换),所以,直观上可用C mn上的向量范数来作为A C m n的矩阵范数。
比如m n 1在∣1 -范数意义下,IIAl1 ;二Ia ijI= tr(A H A) 2; (1.1 )1Zl mn A2在I2-范数意义下,∣∣A∣∣F=∑∑同|2,(1.2)Iy j A J注意这里为了避免与以后的记号混淆,下标用“F”,这样一个矩阵范数,称为Frobenius范数,或F-范数。
可以验证它们都满足向量范数的3个条件。
那么是否矩阵范数就这样解决了?因为数学上的任一定义都要与其对象的运算联系起来,矩阵之间有乘法运算,它在定义范数时应予以体现,也即估计AB的“大小”相对于A与B的“大小”关系。
定义1设A C mn,对每一个A ,如果对应着一个实函数N(A),记为IlAll ,它满足以下条件:(1)非负性:|| A||_0 ;(1 a)正定性:A=O mn= IIAII= 0(2)齐次性:||〉A||=| |||A||, • C ;(3)三角不等式:||A||A B||—||A|| ||B||, -B C m n则称N(A)=|| A||为A的广义矩阵范数。
进一步,若对C m n,C n 1C m l上的同类广义矩阵范数|| || ,有(4)(矩阵相乘的)相容性:|| A || AB ||_|| A|||| B ||, B C n I , 则称N(A) =||A||为A的矩阵范数。
我们现在来验证前面(1.1 )和(1.2 )定义的矩阵范数是否合法?我们这里只考虑(1.2 ),把较容易的(1.1 )的验证留给同学们,三角不等式的验证。
矩阵范数标准详解

《周国标师生交流讲席010》向量和矩阵的范数的若干难点导引(二)一. 矩阵范数的定义引入矩阵范数的原因与向量范数的理由是相似的,在许多场合需要“测量”矩阵的“大小”,比如矩阵序列的收敛,解线性方程组时的误差分析等,具体的情况在这里不再复述。
最容易想到的矩阵范数,是把矩阵m nA C ⨯∈可以视为一个mn 维的向量(采用所谓“拉直”的变换),所以,直观上可用mn C上的向量范数来作为m nA C⨯∈的矩阵范数。
比如在1l -范数意义下,111||||||mniji j A a===∑∑()12tr()HA A =; ()在2l -范数意义下,12211||||||mnF ij i j A a ==⎛⎫= ⎪⎝⎭∑∑, () 注意这里为了避免与以后的记号混淆,下标用“F ”,这样一个矩阵范数,称为Frobenius范数,或F-范数。
可以验证它们都满足向量范数的3个条件。
那么是否矩阵范数就这样解决了因为数学上的任一定义都要与其对象的运算联系起来,矩阵之间有乘法运算,它在定义范数时应予以体现,也即估计AB 的“大小”相对于A B 与的“大小”关系。
定义1 设m nA C ⨯∈,对每一个A ,如果对应着一个实函数()N A ,记为||||A ,它满足以下条件:(1)非负性:||||0A ≥;(1a )正定性:||||0m nA O A ⨯=⇔=(2)齐次性:||||||||||,A A C ααα=∈;(3)三角不等式:||A ||||||||||||,m nA B A B B C ⨯+≤+∀∈则称()||||N A A =为A 的广义矩阵范数。
进一步,若对,,m nn l m l C C C ⨯⨯⨯上的同类广义矩阵范数||||•,有(4)(矩阵相乘的)相容性:||A ||||||||||||AB A B ≤, n lB C⨯∈,则称()||||N A A =为A 的矩阵范数。
我们现在来验证前面()和()定义的矩阵范数是否合法我们这里只考虑(),把较容易的()的验证留给同学们,三角不等式的验证。
矩阵范数及其求导

矩阵范数及其求导在机器学习的特征选择中,利⽤选择矩阵的范数对选择矩阵进⾏约束,即是正则化技术,是⼀种稀疏学习。
矩阵的L0,L1范数为了度量稀疏矩阵的稀疏性,则定义矩阵的⼀种范数,为:∥W∥1=∑i,j|W i,j|。
即为矩阵所有元素的绝对值之和,能够描述接矩阵的稀疏性,但是在优化时,难度较⼤,是将情况向矩阵中元素尽可能是0的⽅向优化。
1)L0范数是指向量中⾮0的元素的个数。
如果我们⽤L0范数来规则化⼀个参数矩阵W的话,就是希望W的⼤部分元素都是0。
换句话说,让参数W是稀疏的。
2)L1范数是指向量中各个元素绝对值之和。
L1范数是L0范数的最优凸近似。
任何的规则化算⼦,如果他在W i=0的地⽅不可微,并且可以分解为⼀个“求和”的形式,那么这个规则化算⼦就可以实现稀疏。
W的L1范数是绝对值,|w|在w=0处是不可微。
3)虽然L0可以实现稀疏,但是实际中会使⽤L1取代L0。
因为L0范数很难优化求解,L1范数是L0范数的最优凸近似,它⽐L0范数要容易优化求解。
矩阵的L2范数L2范数,⼜叫“岭回归”(Ridge Regression)、“权值衰减”(weight decay)。
它的作⽤是改善过拟合。
过拟合是:模型训练时候的误差很⼩,但是测试误差很⼤,也就是说模型复杂到可以拟合到所有训练数据,但在预测新的数据的时候,结果很差。
L2范数是指向量中各元素的平⽅和然后开根。
我们让L2范数的规则项||W||2最⼩,可以使得W的每个元素都很⼩,都接近于0。
⽽越⼩的参数说明模型越简单,越简单的模型则越不容易产⽣过拟合现象。
L1是绝对值最⼩,L2是平⽅最⼩:L1会趋向于产⽣少量的特征,⽽其他的特征都是0,⽽L2会选择更多的特征,这些特征都会接近于0。
矩阵的L2,1范数⽽为了进⼀步说明矩阵的稀疏性,来说明特征选择中矩阵L2,1范数的作⽤。
在特征选择中,通过稀疏化的特征选择矩阵来选取特征,即相当于是⼀种线性变换。
对于特征选择矩阵W,每⼀⾏(即⾏向量)⽤向量的2-范数描述,即。
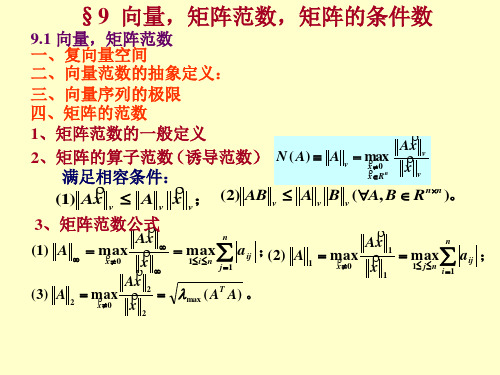
矩阵范数
r r 1) 常向量 b 的扰动 δ b 引起解的误差 δ x r r r r r r r r r −1 + 设 A x = b , A ∃ , x是精确解。 A y = b r δ b 的解记为 y = x + δ x 。 r 是精确解。 r r r r r r 即 A( xr+ δ x ) = b + δ b ⇒ Ax + Aδ x = b + δ b, r r r r r −1 ) 由Ax = b ,得 A(δ xr = δ b,即δ x = A (δ b ), r ( 9 .2 ) ⇒ || δ x ||≤ || A−1 || || δ b ||, r 1 || A || r r 即 r ≤ r , ( 9 .3 ) 又 || b ||=|| Ax ||≤|| A || || x || , r || x || r || b || || δb || x 由(9.2)式及(9.3)式得 || δv || ≤|| A −1 || || A || r )式及( ) || b || || x || 结论: 扰动对解的影响 扰动对解的影响。 结论:b扰动对解的影响。 r r n× n 为精确解, 定理27 (1) A ∈ R 为非奇异矩阵,x为精确解, x = b ≠ 0。 定理 r 为非奇异矩阵, 为精确解 A r r r ( 2)设 A( x + δ x ) = br+ δ b ,则b微小误差 扰动、摄动 引起解 的相 微小误差(扰动 引起解x的相 微小误差 扰动、摄动)引起解 r || δx || || δb || ≤|| A −1 || || A || r . v 对误差有估计式 对误差有估计式: || x || || b || 上式说明,常数项b微小误差引起解的相对误差可能是 说明: 上式说明,常数项 微小误差引起解的相对误差可能是 r 说明: || δb || r 的 || A−1 || || A || 倍。 即上式的不等号中的等号可以成立。 即上式的不等号中的等号可以成立。 || b ||
