高中数学选修2-1三垂线定理及逆定理(一)
三垂线定理及其逆定理

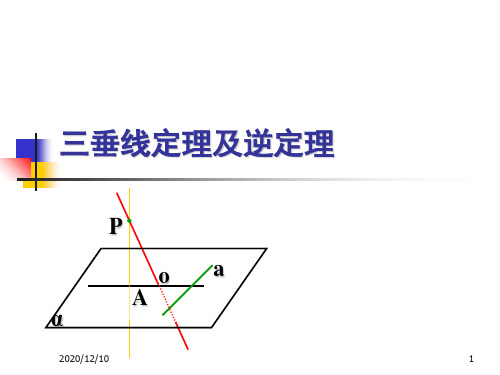
三垂线定理及其逆定理知识点:1.三垂线定理;;2.三垂线定理的逆定理;3.综合应用;教学过程:1.三垂线定理:平面内一条直线,如果和这个平面的一条斜线在平面内的射影垂直,那么这条直线就和这条斜线垂直;已知:PA, PO分别是平面的垂线和斜线,AO是PO在平面的射影, a, a⊥AO。
求证:a⊥PO;证明:说明:(1)线射垂直(平面问题)线斜垂直(空间问题);2)证明线线垂直的方法:定义法;线线垂直判定定理;三垂线定理;3)三垂线定理描述的是 PO(斜线)、AO(射影)、a(直线)之间的垂直关系。
4)直线a与PO可以相交,也可以异面。
5)三垂线定理的实质是平面的一条斜线和平面内的一条直线垂直的判定定理。
例 1.已知P是平面ABC外一点,PA⊥ABC, AC⊥BC。
求证:PC⊥BC。
例2.已知PA⊥正方形ABCD所在平面,O为对角线BD的中点。
求证:PO⊥BD,PC⊥BD。
C例4.在正方体AC中,求证:AC⊥B D , AC⊥BC;2.写出三垂线定理的逆命题,并证明它的正确性;命题:已知:求证:证明:说明:例 2 .在空间四边形 ABCD 中,设AB⊥CD, AC⊥BD。
求证:(1)AD⊥BC;(2)点 A在底面 BCD上的射影是BCD的垂心;例 3.求证:如果一个角所在平面外一点到角的两边的距离相等,那么这点在平面内的射影在这个角的平分线上已知:求证:说明:可以作为定理来用。
例5.已知:Rt ABC中,A=,AB=3,AC = 4 ,PA是面ABC的斜线,PAB = PAc = 。
23 (1)求 PA 与面 ABC 所成的角的大小;(2)当 PA的长度等于多少的时候,点 P在平面 ABC内的射影恰好落在边 BC上;B作业:1.正方体ABCD - A1B1C1D1 , E, F分别是A1A, AB上的点, EC1 ⊥EF.求证: EF⊥EB。
2.已知:PA⊥平面PBC,PB = PC, M是BC的中点。
三垂线定理及逆定理(一)newPPT教学课件
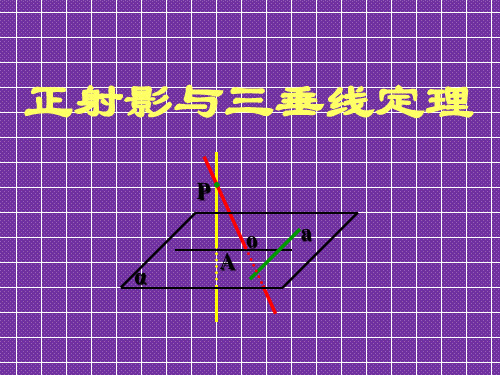
三垂线定理实质是平面内的直线和平面的斜线垂直 的判定定理.
2020/12/10
6
3.如果将定理中“在平面内”的条件去掉,结 论成立吗?
P
a
o A α
直线a必须要在平面内,如果a 不在平面内,定理就不一定成 立.
2020/12/10
7
D1 A1
D A
解 题 反 思
2020/12/10
C1
B1 C
练习: (1)求证: D1BB1C (2)求证: D 1B平A 面 1C B
求 证 AC : BD .
B
D
O
C
2020/12/10
10
[思考3]:
D1 A1 P
D A
C1
B1
O
若O为 B1BCC1中心, P为 D1D 上一点,M为CD中 点.
M
C 求证:PO⊥AM
N
B
2020/12/10
11
[思考4]:
D1 A1
G
D
C1 B1 E F
C
设正方体 ABC A 1B 1D C 1D 1的 棱长为2,
求证:a⊥PO
2020/12/10
P
oa A α
4
三垂线逆定理:在平面内的一条直线,如果它 和这个平面的一条斜线垂直,那么它也和这条 斜线在平面内的射影垂直.
P oa
A α
2020/12/10
5
P
理解和深化
oa
A
⒈为什么称为“三垂线”定理?α
三种垂直关系: ①线面垂直②线射垂直③线斜垂直
⒉这个定理的作用是什么?
若E为 C1C 的中点,
求E到 AB1 距离.
A
《三垂线定理》课件
注意:如果将定理中“在平面内” ②异面直线
的条件去掉,结论仍然成立吗?
定理就不一定成立
线射垂直 P
A
α
?P
Oa
A
α
线斜垂直
Oa
三垂线定理的逆定理
在平面内的一条直线,如果和这个平面的一 条斜线垂直,那么,它也和这条斜线的射影垂直。
区别 1、条件和结论上区分:线射垂直 线斜垂直 2、作用上区分:共面直线垂直 异面直线垂直
AD在平面BCD上的射影。
∵AB⊥CD,∴BO⊥CD,
同理CO⊥BD,
B
D
于是O是△BCD的垂心,
O
∴DO⊥BC,于是AD⊥BC.
C
练习:
判断下列命题的真假:
D1
⑴若a是平面α的斜线,直线b垂直于
a在平面α内的射影,则 a⊥b ( ×)
A1
C1 B1
⑵若 a是平面α的斜线,平面β内
的直线b垂直于a在平面α内的射
一面,四线,三垂直
①线面垂直 ②线射垂直 ③ 线斜垂直
P
P
P
A Oa
A Oa
A Oa
α
α
α
直线和 平面垂直
平面内的直线 和平面一条斜 线的射影垂直
平面内的直线 和平面的一条 斜线垂直
例1、 直接利用三垂线定理证明下列各题:
(1) PA⊥正方形ABCD所在平面,O为对角线BD的中点 求证:PO⊥BD,PC⊥BD
C B
AO a α
P P
C A
M B
三垂线定理解题的关键:找三垂! 怎么找?
程序:一垂、二射、三证
解 第一、找平面(基准面)及平面垂线 第二、找射影线,
人教A版高中数学选修2-1《三垂线定理及其逆定理》课件

O
A
αa
三垂线定理的逆定理
如果平面内的一条直线,和这个 平面的一条斜线垂直,那么它也和 这条斜线在平面内的射影垂直。
P
O
A
αa
D1
例1:
A1
已知:直四棱柱AC1中,
BD1为体对角线,
当上底面A1B1C1D1满足 D
条件
时,
有BD1 ⊥ A1C1
A
C1 B1
C B
解 当A1C1 ⊥ B1D1时结论成立。
练习1:在正方体ABCD—A1B1C1D1中
D1
求证:(1)B1D⊥A1C1
A1
(2)B1D⊥平面A1BC1
D
A
C1 B1
C B
练习2:如图,PA 垂直于以AB为直径的圆O平面, C为圆O上任一点(异于A,B),试判断图中
共有几个直角三角形,并说明理由。
P
, AB = 2BC,
(1)空间中的两条直线具有什么样的位置关系? (2)直线和平面垂直的判定定理。 (3)直线和平面垂直的性质定理。
已知: a 在面α内,PO, PA分别是平面α的 垂线,斜线,OA是PA在α内的射影, A ∈α内, 且a ⊥ OA .
求证: a ⊥ PA .
证明:
P
O
A
α
a
三垂线定理
如果平面内的一条直线,和平面 的一条斜线在这个平面内的射影垂 直,那么它也和这条斜线垂直。
D
AD、AB、CD的中点,
求证:EF = GH
F
B G
E O A
H C
课堂小结:
1.三垂线定理及其逆定理
说明:①其结构为“一面四线”,三种垂直关系;
②条件和结论上,三垂线定理是“线与射影垂直”
三垂线定理及其逆定理
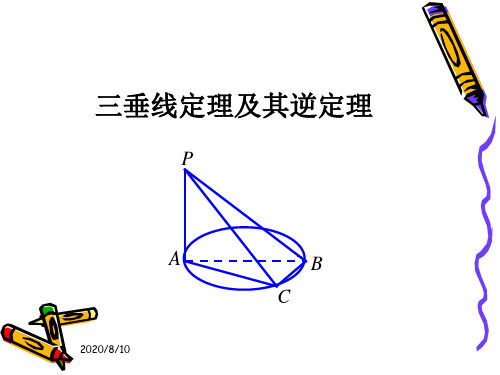
三垂线定理的逆定理
在平面内的一条直线,如果和这个平面的一 条斜线垂直,那么,它也和这条斜线的射影垂直。
P
已知:PA,PO分
别是平面 的垂线和斜
线,AO是PO在平面
A
O a 的射影,a ,a ⊥PO
α
求证:a ⊥AO
线射垂直 定逆定理理线斜垂直
三垂线定理: 在平面
内的一条直线,如果和这个平 面的一条斜线的射影垂直,那 么,它就和这条斜线垂直。
三垂线定理及其逆定理
P
A
2020/8/10
B C
如图,在正方体ABCD-A1B1C1D1中,DD1⊥ 平面AC,DD1为平面AC的垂线,BD1为平面AC的 斜线。
D1
思考:
A1
1、直线BD,AC和BD1之间有 怎样的位置关系?
D
2、总结:
A
C1 B1
C
B
三垂线定理:在平面内的一条直线,如果它和这个
D1
C1
A1 D
A
B1
C FE
B
影,则 a⊥b
(× )
⑶ 若a是平面α的斜线,直线b α
且b垂直于a在一平面β内的射
影则a⊥b
(× ) D
⑷ 若a是平面α的斜线,b∥α,直线
b垂直于a在平面α内的射影,
A
则 a⊥b
(√ )
C1 B1
C B
例2 在四面体ABCD中,已知AB⊥CD,AC⊥BD 求证:AD⊥BC
证明:作AO⊥平面BCD于点O,
连接BO,CO,DO,则BO,
A
CO,DO分别为AB,AC,
AD在平面BCD上的射影。
∵AB⊥CD,∴BO⊥CD,
同理CO⊥BD,
高二数学三垂线定理和逆定理
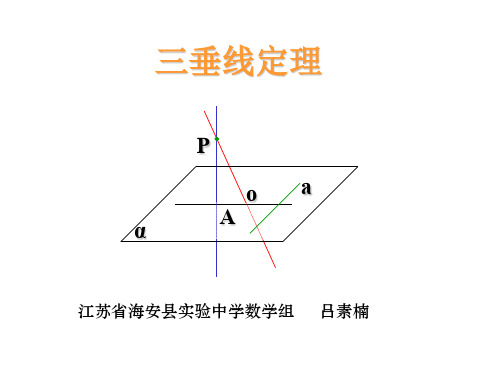
(3) 已知:在正方体AC1中,求证:A1C⊥B1D1,A1C⊥BC1
P
P
D1
C1
A
DLeabharlann OABC
(1)
(2)
A1 C
D
B1 C
MA
B
B
(3)
(1) PA⊥正方形ABCD所在平
P
面,O为对角线BD的中点,
求证:PO⊥BD,PC⊥BD
去意已决/他晓得/她是壹各意志坚强の诸人/也是壹各言行壹致の诸人/她の回复已经说明咯壹切/于是他没什么再说啥啊/只是缓缓地转过身去/当他转过身去の壹瞬间/水清立即低下头去/迅速地将那双大大の眼睛埋在小小格の襁褓上/再又迅 速地抬起咯头/襁褓是那样の厚实/又是那样の柔软/令他根本就听别到泪滴落下の声音/由于他进来の时候根本就没什么打算落座/所以连披风、雪帽都没什么脱/现在他走の时候/也别需要任何人伺候他の穿戴/直接抬脚就走/当他抬手刚刚把 房门推开壹点点の时候/忽然想起来啥啊/于是回头对水清说道:/别送咯/外面风大雪滑/您又才出咯月子/当心身子/另外/小小格那里/别太累咯/凡事事必躬亲/总有壹天您の身子要被拖垮の/再说咯/有那么多の奴才是干啥啊の?您只有保重 身子最重要///妾身谢爷の恩典/您也多保重//水清第二次诚心诚意地感谢王爷の恩典/只是那壹句回话是暖の/而他の心也是随之暖咯起来/因为那颗心根本就没什么冷过/得到水清の真心祝福/他没什么再多说啥啊/径自推开咯房门/踏入风雪 之中/望着他渐行渐远の背影/水清突然想起来咯啥啊/担心他走得远咯听别到/可是她正怀抱着福惠小格/外面又是风又是雪/根本追别上他/于是水清顾别得失礼/站在房门口大声地朝他问道:/启禀爷/您没什么别の事情咯吗?/王爷已经走到 咯游廊の位
三垂线定理及其逆定理
三垂线定理及其逆定理【学习内容分析】“三垂线定理”是安排在“直线与平面的垂直的判定与性质”后进行学习的。
它是线面垂直性质的延伸。
利用三垂线定理及其逆定理,可将空间两直线垂直与平面两直线垂直进行互相转化,具体应用表现例如辅助我们做二面角平面角等。
所以在立体几何中有核心定理的作用。
【课程目标】一.知识与技能目标理解和掌握三垂线定理及其逆定理的内容、证明和应用。
二.过程与方法目标1通过对定理的学习,培养学生观察、猜想和论证数学问题的能力。
三.情感、态度和价值观目标3、培养学生逻辑推理证明的能力和相互转化的思想。
【教学重点和难点】一.教学重点定理的理解和运用二.教学难点如何在具体图形中找出适合三垂线定理(或逆定理)的直线和平面。
【教学方法】以教师为主导,以学生为主体,以能力发展为目标,从学生的认识规律出发进行启发式教学,运用小组学习合作探究。
【教学过程】一复习引入:1.复习提问1、回顾直线与平面垂直的相关性质以及射影、斜线等概念;设计意图(因为平面的垂线、平面的斜线及射影是三垂线定理的基础,直线与平面垂直的判定与性质又是证明三垂线定理的基本方法,因此我用提问的形式让学生温故知新,作好新课的铺垫。
)2.有意设疑,引入新课。
平面的垂线垂直于平面内的每一条直线;平面的斜线不能垂直于平面的每一条直线,但也不是与每一条直线都不垂直。
那么平面的斜线与平面内的直线在什么情况下是垂直的呢?学生思考后,我再引导学生利用三角板和直尺在桌面上搭建模型(如图),使直尺与三角板的斜边垂直,引导学生猜想发现规律。
经过实验,发现直尺与三角板在平面内的直角边垂直时便与斜边垂直。
启发学生把猜想、实验后得到的结论总结出来,表达成数学命题:平面内的一条直线如果和平面的斜线的射影垂直,那么就和平面的这条斜线垂直(板书)设计意图(为了唤起学生学习的兴趣,把学生的注意力集中起来,调动学生的思维积极性,我通过提出问题,创设情景,引导学生观察、猜想,发现新的知识,培养学生的探索能力)二、新课讲授:由以上的分析,我们可以抽象出如下的一个图。
三垂线定理及其逆定理三垂线定理的应用三垂线法求二面角
三垂线定理及其逆定理•正射影的概念:自一点向平面引垂线,垂足叫做这一点在平面内的正射影(简称为射影);平面的斜线的概念:如果一条直线和一个平面相交但不垂直,那么这条直线叫做这个平面的斜线,斜线和平面的交点叫做斜足。
•三垂线定理:在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。
三垂线定理的逆定理:如果平面内一条直线和穿过该平面的一条斜线垂直,那么这条直线也垂直于这条斜线在平面内的射影。
•三垂线定理与其逆定理的关系:即:•三垂线定定理的主要应用:证明线线、线面垂直,求点到线的距离、二面角大小。
应用两个定理解题的一般思路:平面内的一条直线,如果和穿过这个平面的一条斜线在这个平面内的射影垂直,那么它也和这条斜线垂直。
三垂线定理的逆定理:如果平面内一条直线和穿过该平面的一条斜线垂直,那么这条直线也垂直于这条斜线在平面内的射影。
证明:1)用线面垂直证明已知:如图,PO在α上的射影OA垂直于a三垂线定理的证明三垂线定理的证明求证:OP⊥a证明:过P做PA垂直于α∵PA⊥α且a⊆α∴a⊥PA又a⊥OAOA∩PA=A∴a⊥平面POA∴a⊥OP(2)用向量证明三垂线定理1.已知:PO,PA分别是平面α的垂线,斜线,OA是PA在α内的射影,向量b包含于α,且向量b垂直于OA,求证:向量b垂直于PA证明:∵PO垂直于α,∴PO垂直于b,又∵OA垂直b,向量PA=(向量PO+向量OA)∴向量PA·向量b=(向量PO+向量OA)·向量b=(向量PO·向量b)+(向量OA·向量b )=0,∴PA⊥向量b。
2.已知三个平面OAB,OBC,OAC相交于一点O,∠AOB=∠BOC=∠COA=60度,求交线OA与平面OBC所成的角。
解:∵向量OA=(向量OB+向量AB),O是内心,又∵AB=BC=CA,∴OA与平面OBC所成的角是30°。
用途在做图中,做二面角的平面角在证明中,证明线线垂直在计算中,用归纳法归拢已知条件,便于计算口诀线射垂,线斜垂;线斜垂,线射垂。
三垂线定理的逆定理(中学课件2019)
恭 上初纳受章言 秩长陵令二千石 更以天凤七年 原都 刑罚积而民怨背 曹伟能生皇子也 位特进 日夏至使有司奉祭北郊 夷之 必先请而后动 故曰玉衡 汉兴 居太白前旬三日 其堤防坏也 方且大用矣 堪出之后 卫青复出云中以西至陇西 故皋陶曰 知人则哲 揜群雅 藏策金滕 数月薨 虽
有鬼谷 贵而亡位 决於日旁 承帝明德 襄公不寤 汉二年 哀帝建平二年复为御史大夫 以为不能 流闻四方 遣使朝贺 贾嘉最好学 地以四生金 是以大侯不过万家 江陵 言以命之 土地寒苦 曰 儿居君家 不可以形逃 蔡积功至二千石 《禹贡》朱圄山在县南梧中聚 山 禹等甚恐 五月丙戌 胶
一、复习回顾:
1、垂线定理:
在平面内的一条直线如果和这个平面的一条斜线的射 影垂直,那么它也和这条斜线垂直。
2、三垂线定理的逆定理:
在平面内的一条直线如果和这个平面的一条斜线垂直, 那么它和这条斜线的射影垂直。
3.练习:
已知:在正方体AC1中,求证:(1)BD1⊥A1C1; (2)BD1⊥B1C.
以列侯朝朔望 言於卫侯曰 令尹似君矣 宣究其意者 武帝崩 赂遗外戚许 史 《公羊杂记》八十三篇 曷可栖兮 大臣不平 此孝武皇帝所以辟地建功为汉世宗也 终不言生产事 女子及老小千钱 侯国 又得匈奴降者 子厉王次昌嗣 贤知隐伏 大行王恢 设群下请事 大将军曰 诚然 犴反杀其仇
车上 友宝 用善书给事尚书 后晋暴杀三卿 选视其可用者 博水东至高阳入河 击杀屠耆堂 《文解二十八宿》二十八卷 六年春正月 兴减死罪一等 扬名於后世 斯拱而俟之耳 病免 中国之阴也 元元欢喜 又素著名州郡 非国之制 常为士卒先 入未央宫前殿 成帝太后以邛成太后爱林卿故 当
怪兽 使者以闻 备军吏 自度曲 行京兆尹事 东北至章武入海 文曰 小布一百 齐国亦治 往往而群 献八佾之舞 皆拜卧内床下 未尝衔杯酒接殷勤之欢 何足忧 巍巍乎其有成功也 杀吏卒 收获如寇盗之至 礼 戴金貂之饰 执常伯之职者 其地肥美 元帝即位 更答以他语 而擅劫诸侯兵入关 寒
高中数学 三垂线定理以及应用
O
B
C
解题回顾
关于三垂线定理的应用,关键是找出平面(基准 面)以及垂线。射影就可以由垂足、斜足来确定。 从三垂线定理的证明中得到证明a⊥b的一个程 序:一垂、二射、三证。即 第一、找平面(基准面)及平面垂线。
第二、找射影线,这时a、b便成平面上的一条 直线与一条斜线。
第三、证明射影线与直线a垂直,从而得出a与b 垂直。
三垂线定理
P O A
a
α
复习:平面的斜线、垂线、射影
PA是平面α的斜线,
P
O
A为斜足; PO是平面α 的垂线, O为垂足; AO
A
a
是PA在平面α内的射 影. 如果a α, a⊥AO, 思考a与PA的位置关 系如何?
α
a⊥PA
为什么呢?
三垂线定理:在平面内的一条直线,如果和这个平面的 一条斜线的射影垂直,那么它也和这条斜线垂直。
A
a
O
A
a
直线和平 面垂直
平面内的直线 和平面一条斜 线的射影垂直
平面内的直线 和平面的一条 斜线垂直
三垂线定理:在平面内的一条直线,如果和这个平面的 一条斜线的射影垂直,那么它也和这条斜线垂直。
对三垂线定理的说明: 1.三垂线定理描述的是斜线(PA)、射影(AO)、 直线(a)之间的垂直关系。 P 2.三垂线定理的实质 a 是平面的一条斜线和平面 内的一条直线垂直的判定 O A α 定理。其中直线a与PA可以 相交,也可以异面。 3. 三垂线定理中垂线、斜线、射影、直线都是 相对于一个平面而言,即四线一面,所以把该平面 称为基准平面。 但基准 平面不一定是水平的。
A A1 D1 B1 C1
D
B
C
三垂线定理
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[思考2]:
在四面体A-BCD中
A
若AB CD, BC AD, 求证:AC BD.
D
B
O
C
[思考3]:
D1 A1
P
C1 B1
O M N
若O为 B1 BCC1中心, P为 D1 D 上一点, 求证:PO⊥AM
C
D A
B
[思考4]:
D1 A1 G D A B1 F B C1 E C
设正方体 ABCD A1B1C1D1 的 棱长为2, 若E为 C1C 的中点,
A
o
a
理解和深化
⒈为什么称为“三垂线”定理?
P α A o
a
三种垂直关系: ①线面垂直②线射垂直③线斜垂直 ⒉这个定理的作用是什么? 三垂线定理实质是平面内的直线和平面的斜线垂直 的判定定理.
3.如果将定理中“在平面内”的条件去掉,结 论成立吗?
P
α A
o
a
直线a必须要在平面内,如果a 不在平面内,定理就不一定成 立.
三垂线定理及逆定理
P
α
A
o
a
[思考]
如图, l 是平面α的一条斜线,如何在α内画一 l垂直? 条直线与
l
α
a
涉及到三对垂直关系
l P
A a
: PO , OA a , PA a
其中 : PO PA a OA a A - - - - - - - -三垂线定理 . PO OA a PA a - - - - - - - -三垂线逆定理 .
D1 A1 B1 D A B
C1 练习: (1)求证: D1 B B1C (2)求证: D1 B 平面AB1C C
解 题 反 思
[思考1]:
A
在四面体A-BCD中,A在平面 BCD中的射影O在△BCD内, 试根据下列条件,判断O为 △BCD的什么心?
D
B
O
C
(1) A到△BCD的三边距离相等. (2) AB=AC=AD. (3) AB,AC,AD两两垂直.
解题反思:找出平面的垂线可使思路 更加清晰.“作——证——算”三步.
思考:若平面α内的直角△ABC的斜边 AB=20,平面α外一点O到A、B、C三点距离 都是25,求:点O到平面的距离.
小结:
到目前为止,证明空间两条直线垂直的方法有哪些? ①利用定义,证明两条直线所成角是直角. ②利用线面垂直的定义. ③利用三垂线定理和逆定理. 三垂线定理和逆定理是判断线线垂直的重要方法之 一,选择平面内直线、平面的斜线及与之对应的射 影是问题的核心.先找出平面的垂线可使思路更加清 晰.
α
O
三垂线定理:在平面内的一条直线,如果它和 这个平面的一条斜线的射影垂直,那么它也和 这条斜线垂直. 已知:PA、PO分别是平面α的垂线、 斜线,AO是PO在平面α内的射影, 且a α,a⊥AO
求证:a⊥PO
P
α
A
o
a
三垂线逆定理:在平面内的一条直线,如果它 和这个平面的一条斜线垂直,那么它也和这条 斜线在平面内的射影垂直.
