控制系统仿真大作业
控制系统仿真大作业

控制系统仿真论文上了控制系统仿真这门课后,我结合自己现在所做的课题写了一些心得和感想。
我现在做的项目名字叫做《高精度实时导航技术》,主要是结合我国在导航定位领域的发展需求,通过分析卫星高精度定轨误差,研究卫星高精度定轨方法并通过利用低轨卫星进行导航增强的机理和方法研究,来提升我国高精度实时导航定位的能力和导航系统的可用性、完好性和抗干扰能力。
其中我所做的一个部分需要模拟卫星轨道数据,尤其是低轨卫星的,需要通过STK(航天卫星工具)仿真软件,仿真低轨卫星星座构型希望能够保证最少LEO微小卫星数量最少来实现LEO+BD下的PPP(单点精密定位)全球覆盖。
这个过程中我们通过STK软件模拟的低轨卫星来研究其的全球覆盖性,从而得到最优星座构型。
因此我主要谈一下关于使用STK仿真的过程和心得:为什么要仿真?因为仿真系统是可以取得很高的经济效益。
系统仿真是20世纪40年代末以来伴随着计算机技术的发展而逐步形成的一门新兴学科。
仿真(Simulation)就是通过建立实际系统模型并利用所见模型对实际系统进行实验研究的过程。
最初,仿真技术主要用于航空、航天、原子反应堆等价格昂贵、周期长、危险性大、实际系统试验难以实现的少数领域,后来逐步发展到电力、石油、化工、冶金、机械等一些主要工业部门,并进一步扩大到社会系统、经济系统、交通运输系统、生态系统等一些非工程系统领域。
可以说,现代系统仿真技术和综合性仿真系统已经成为任何复杂系统,特别是高技术产业不可缺少的分析、研究、设计、评价、决策和训练的重要手段。
其应用范围在不断扩大,应用效益也日益显著。
系统仿真是建立在控制理论、相似理论、信息处理技术和计算机初等理论基础之上的,以计算机和其他专用物理效应设备为工具,利用系统模型对真实或假设的系统进行试验,并借助于专家的经验知识、统计数据和信息资料对实验结果进行分析研究,进而做出决策的一门综合的实验性学科。
从广义而言,系统仿真的方法适用于任何的领域,无论是工程系统(机械、化工、电力、电子等)或是非工程系统(交通、管理、经济、政治等)。
自动控制仿真大作业
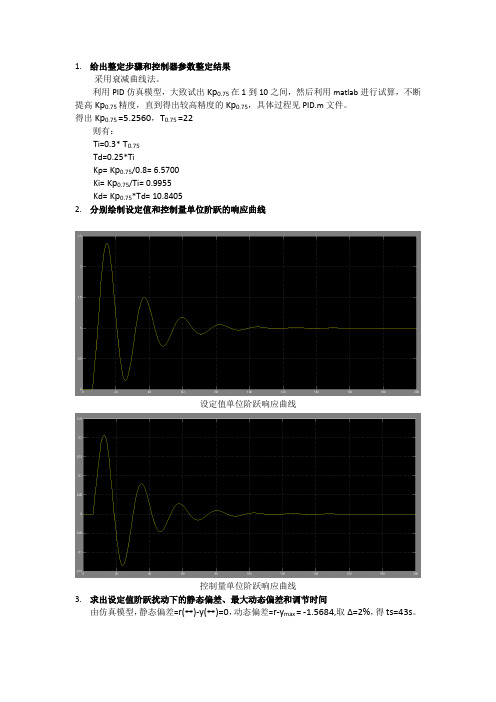
1.给出整定步骤和控制器参数整定结果采用衰减曲线法。
利用PID仿真模型,大致试出Kp0.75在1到10之间,然后利用matlab进行试算,不断提高Kp0.75精度,直到得出较高精度的Kp0.75,具体过程见PID.m文件。
得出Kp0.75 =5.2560,T0.75 =22则有:Ti=0.3* T0.75Td=0.25*TiKp= Kp0.75/0.8=6.5700Ki= Kp0.75/Ti=0.9955Kd= Kp0.75*Td=10.84052.分别绘制设定值和控制量单位阶跃的响应曲线设定值单位阶跃响应曲线控制量单位阶跃响应曲线3.求出设定值阶跃扰动下的静态偏差、最大动态偏差和调节时间由仿真模型,静态偏差=r(∞)-y(∞)=0,动态偏差=r-y max = -1.5684,取Δ=2%,得ts=43s。
PID.m程序代码如下:%第一问,采用衰减曲线法Ki = 0;Kd = 0;for Kp = 1:0.1:10;%粗选Kpsim('PID1.mdl');index=find(diff(sign(diff(y)))==-2)+1;%网上百度到的,用来寻找数据中极大值的位置,index 记录数据位置if length(index)>=3 %输出是震荡的前提M1=y(index(1))-y(length(y));%y(index(1))为第一个极大值,默认最后一个y即y(length(y))为稳定值M3=y(index(2))-y(length(y));%y(index(2))为第二个极大值a=(M1-M3)/M1;%a为衰减率if abs(a-0.75)<0.01temp=Kp;%存储粗选出的Kpbreak;endendendfor Kp = temp-0.1:0.01:temp+0.1;%进一步缩小Kp范围sim('PID1.mdl');index=find(diff(sign(diff(y)))==-2)+1;if length(index)>=3M1=y(index(1))-y(length(y));M3=y(index(2))-y(length(y));a=(M1-M3)/M1;if abs(a-0.75)<0.001%增大精度temp=Kp;break;endendendfor Kp = temp-0.01:0.001:temp+0.01;%精选出Kpsim('PID1.mdl');index=find(diff(sign(diff(y)))==-2)+1;if length(index)>=3M1=y(index(1))-y(length(y));M3=y(index(2))-y(length(y));a=(M1-M3)/M1;if abs(a-0.75)<0.0001kp=Kp;disp('Kp(0.75)=')%输出显示Kp(0.75)disp(kp)T=t(index(2))-t(index(1));%计算震荡周期disp('T(0.75)=')%输出显示T(0.75)disp(T)break;endendendti=0.3*T;%求出Kp,Ki,Kdtd=0.25*ti;Kp=kp/0.8Ki=Kp/tiKd=Kp*td%第二问直接修改仿真模型的设定值和控制量,然后仿真即可%第三问sim('PID1.mdl');index=find(diff(sign(diff(y)))==-2)+1;e=1-y(length(y))%静态偏差eM=1-y(index(1))%动态偏差for index=1:1:length(y)if abs(y(index)-y(length(y)))<=0.02*y(length(y))%找出调整时间对应的y的位置,取Δ=2% ts=t(index)%调整时间break;endend搭建的simulink模型如下:。
二阶弹簧-阻尼系统PID参数整定《控制系统仿真与CAD》MATLAB版

《控制系统仿真与CAD》大作业一、提交内容和评分标准1、大作业word文档(.doc格式),包括:每道题目的程序(有必要的注释)、程序运行结果、结果分析。
此项占大作业成绩的50%。
2、5分钟的汇报视频文件(.mp4格式),汇报视频需用EV录屏软件(EVCapture,学习通“资料”栏目里可下载)录制,用这个软件对着程序讲解,录成一个mp4视频文件(打开录屏软件,点击开始录制,打开程序,对着麦克风说话,可以随时停止,结束后自动生成视频文件)。
此项占大作业成绩的50%。
二、提交协议(非常重要!)1、截至时间:2020年6月17日(周三)晚上20点。
2、提交方式:学习通“作业”栏目里,文件夹命名为学号_姓名(比如201710230001_张三),文件夹中需包括大作业word文档(.doc格式),汇报视频文件(.mp4格式),word文档和汇报视频文件命名与文件夹一样。
三、注意事项1、两人雷同分数/2,三人雷同/3,以此类推。
2、没有做任何修改将例题、平时作业或阶段练习程序交上来,分数为0。
四、题目:以下四道题,任选一题完成,尽可能使用本课程学习的各种函数和分析方法。
选题一:二阶弹簧—阻尼系统的PID控制器设计及参数整定考虑弹簧-阻尼系统如图1所示,其被控对象为二阶环节,传递函数()G s如下,参数为M=1kg,b=2N.s/m,k=25N/m,()1F s 。
设计要求:用.m文件和simulink模型完成(1)控制器为P控制器时,改变比例系数大小,分析其对系统性能的影响并绘制相应曲线。
(2)控制器为PI控制器时,改变积分系数大小,分析其对系统性能的影响并绘制相应曲线。
(例如当Kp=50时,改变积分系数大小)(3)设计PID控制器,选定合适的控制器参数,使闭环系统阶跃响应曲线的超调量σ%<20%,过渡过程时间Ts<2s, 并绘制相应曲线。
图1 弹簧-阻尼系统示意图弹簧-阻尼系统的微分方程和传递函数为: F kx x b x M =++&&& 25211)()()(22++=++==s s k bs Ms s F s X s G图2 闭环控制系统结构图选题二:Bode 图法设计串联校正装置考虑一个单位负反馈控制系统,其前向通道传递函数为:()(1)(4)o K G s s s s =++ 设计要求:1、分析校正前系统的性能及指标2、应用Bode 图法设计一个串联校正装置()c G s ,使得校正后系统的静态速度误差系数110v K s -=,相角裕量50r =o ,幅值裕量10g K dB ≥。
控制系统仿真作业D

提交作业时,应包括系统仿真模型截图和用MATLAB语句绘出的系统输出图形。
答:
系统仿真模型截图:
Soope:
Soope1:
语句绘出系统输出图形:
plot(simout.time,simout.signals.values)
题目二:使用s函数实现下述状态空间表示的LTI动态系统,并用Matlab simulink提供的模块进行阶跃响应比较。
幅值为1周期为50s的方波信号用输出到workspace中的数据用matlab语句绘出系统输出图形提交作业时应包括系统仿真模型截图和用matlab语句绘出的系统输出图形
题目一:使用Matlab simulink编制下图所示的系统仿真模型,并
选择仿真参数:起始时间0s,结束时间100s
输入信号:幅值为±1,周期为50s的方波信号
答:模响应:
语言响应:
控制系统仿真实验报告1

昆明理工大学电力工程学院学生实验报告实验课程名称:控制系统仿真实验开课实验室:年月日实验一 电路的建模与仿真一、实验目的1、了解KCL 、KVL 原理;2、掌握建立矩阵并编写M 文件;3、调试M 文件,验证KCL 、KVL ;4、掌握用simulink 模块搭建电路并且进行仿真。
二、实验内容电路如图1所示,该电路是一个分压电路,已知13R =Ω,27R =Ω,20S V V =。
试求恒压源的电流I 和电压1V 、2V 。
IVSV 1V 2图1三、列写电路方程(1)用欧姆定律求出电流和电压 (2)通过KCL 和KVL 求解电流和电压四、编写M文件进行电路求解(1)M文件源程序(2)M文件求解结果五、用simulink进行仿真建模(1)给出simulink下的电路建模图(2)给出simulink仿真的波形和数值六、结果比较与分析实验二数值算法编程实现一、实验目的掌握各种计算方法的基本原理,在计算机上利用MATLAB完成算法程序的编写拉格朗日插值算法程序,利用编写的算法程序进行实例的运算。
二、实验说明1.给出拉格朗日插值法计算数据表;2.利用拉格朗日插值公式,编写编程算法流程,画出程序框图,作为下述编程的依据;3.根据MATLAB软件特点和算法流程框图,利用MATLAB软件进行上机编程;4.调试和完善MATLAB程序;5.由编写的程序根据实验要求得到实验计算的结果。
三、实验原始数据上机编写拉格朗日插值算法的程序,并以下面给出的函数表为数据基础,在整个插值区间上采用拉格朗日插值法计算(0.6)f,写出程序源代码,输出计算结果:四、拉格朗日插值算法公式及流程框图五、程序代码六、计算结果f=(0.6)实验三 动态电路的建模及仿真一、实验目的1.了解动态电路的理论,掌握动态电路建模的基本原理; 2.熟悉MATLAB 的Simulink 模块,并掌握使用模块搭建过程。
二、实验说明电力系统是一个大规模、时变的复杂系统,主要由发电、变电、输电、配电和用电等环节组成,在国民经济中占有非常重要的作用。
控制系统仿真试题及答案

《控制系统仿真》期终考查试题学生姓名:学号:班级:自动化101学院:电气工程学院老师:吴钦木2013 年12 月24 日一、程序设计题(给出程序和运行结果) 1、请编程实现求取满足12010mi i =>∑的m 的最小值。
答:>> mysum=0; >> for m=1:2010 mysum=mysum+m;if(mysum>2010)break;end end >> m m =63 >>2、已知多项式21()359f x x x =-+,22()41f x x x =+-,试编程求312()()()0f x f x f x =⨯=的解,并找出其解大于零的值。
答:>> p1=[3 -5 9]; >> p2=[1 4 -1]; >> p=conv(p1,p2); >> x=roots(p); >> b=x>0; >> c=x(x>0) c =0.8333 + 1.5184i 0.8333 - 1.5184i 0.2361 >>二、作图题(给出程序和运行结果)1、 已知220s in 100U t π=(伏), 23)B U t ππ=+(伏),43)C U t ππ=+(伏),0t =~0.1(秒),请利用MA TLAB 软件在一个图形界面的三个不同区域分别绘制A U ,B U ,C U 相对于时间t 的波形,并要求图形区域有栅格。
答:>> t=0:0.001:0.1;ua=220*sqrt(2)*sin(100*pi*t); subplot(3,3,1); plot(t,ua); gridub=220*sqrt(2)*sin(100*pi*t+2*pi/3);subplot(3,3,2); plot(t,ub); griduc=220*sqrt(2)*sin(100*pi*t+4*pi/3); subplot(3,3,3); plot(t,uc); gridA U ,B U ,C U 相对于时间t 的波形2、 已知一系统的传递函数为325()362s G s s s s +=+-+试利用MA TLAB 建立系统的零极点传函表达式和状态空间表达式,并绘制出系统的单位阶跃响应图。
控制系统仿真实验(1-10)

控制系统仿真(Matlab)实验实验1:初步了解MATLAB环境及命令窗口的使用一、课堂练习1、掌握MATLAB的启动方式;熟悉MATLAB的命令窗口;熟悉常用的选单和工具栏;熟悉MATLAB桌面的其他窗口。
2、熟悉MATLAB命令窗口中的选单“File”的功能。
3、在命令窗口中输入以下命令并查看运行结果:>>a=2.5>>b=[1 2;3 4]>>c=‟a‟>>d=sin(a*b*pi/180)>>e=a+c4、根据3题分别输入以下命令查看运行结果。
(1)使用标点符号来修改命令行①;:不显示计算结果【注意与回车键比较运行结果】>>a=2.5;②%:用做注释>> b=[1 2;3 4] % b为矩阵(2)通过常用操作键来编辑命令①↑:向前调回已输入过的命令行②↓:向后调回已输入过的命令行③Esc:消除当前行的全部内容(3)查看工作空间窗口:在工作空间中使用who,whos,clear 命令,观察运行结果。
5、熟悉MATLAB环境。
(1)MATLAB命令窗口:菜单命令各项的作用;工具栏各项功能,要求熟练使用工具栏按钮;熟练使用命令编辑区中命令窗口快捷键的功能。
(2)了解MATLAB的程序编辑器。
(3)熟悉MATLAB的work子目录。
(4)MATLAB运行外部环境:进入DOS操作系统。
6、标点符号可以使命令行不显示运算结果,用来表示该行为注释行。
二、课外练习1、MATLAB强大的绘图功能(1)采用插值方式绘制海底形状图。
具体程序如下:>>xi=linspace(-5,5,50);yi=linspace(-5,5,50)>>[XI,YI]=meshgrid(xi,yi);>>ZI=interp2(x,y,z,XI,YI,‟*cubic‟);>>Surf(XI,YI, ZI),view(-25,25)(2)绘制草帽图具体程序如下:>>[x,y]=meshgrid(-8:0.5:8);>>r=sqrt(x.^2+y.^2)+eps;>>z=sin(r)./r;>>surf(x,y,z)>>shading interp>>axis off(3)绘制圆球球体具体程序如下:>>sphere(100);axis equal;>>shading flat;camlight right;>>camlight left;lighting phong2、MATLAB程序流程控制(1)在M文件编辑器中输入以下程序,并观察运行结果。
MATLAB与控制系统仿真大作业

>> G1=tf(num,den);
>> G1=zpk(G1)
G1 =
5 (s+0.6) ----------------(s+3) (s+2) (s+1)
>> num=[2 1]; den=[1 2.9 1]; G2=tf(num,den); >> G2=zpk(G2)
G2 =
2 (s+0.5)
>> xlabel('x') ylabel('exp(-2.*x)')
三、simulink 建模(每题 10 分,共 20 分)
1、已知单位负反馈的开环传递函数为 G(s) =
2 s2 + 4s
,试利用
simulink
建立系在单位阶跃输入作用下的模型。
要求答案包括:(1)simulink 建模结构图;
(2)在同一个坐标中的阶跃信号和响应曲线图。
2、已知系统的开环传递函数为
G1(s)
=
2s2 + 5s + 6 s2 + 2s + 3
、G2 (s)
=
s2
s+6 + 7s +1
,H
(s)
=
5(s + 2) s +10
求:建立 Simulink 仿真模型,并求出其系统在单位阶跃响应;
要求答案包括:(1)simulink 建模结构图;
x=
-2.9709
0.5491
3.6000
0.0509
2. 已知下列矩阵
2 3 1
−1 3 5
A
=
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
控制系统仿真实验报告专业班级:自动F0903 姓名:罗新勇学号: 200948280311 指导教师:张杰实验一、熟悉MATLAB 环境及矩阵、数组的数学计算一、 实验目的1、熟悉启动和退出Matlab 的方法;2、熟悉Matlab 命令窗口的组成;3、掌握建立矩阵的方法;二、 实验内容:1、帮助命令使用help 命令,查找 sqrt (开方)函数的使用方法;2、先求下列表达式的值,然后显示Matlab 工作空间的使用情况并保存全部变量。
.3,9.2,8.2,...,8.2,9.2,0.3,23.0ln)3.0sin(2)3(545.0212),1log(21)2(185sin 2)1(3.03.0322201---=+++-=⎥⎦⎤⎢⎣⎡-+=++=+=-a a a e ez i x x x z e z aa 其中提示:利用冒号表达式生成a 向量,求各点的函数值时用点乘运算。
⎪⎩⎪⎨⎧=<≤+-<≤-<≤=5.2:5.0:0,32,1221,110,)4(2224t t t t t t t t z 其中提示:用逻辑表达式求分段函数值。
(1)z1=2*sin(85/180*pi)/(1+(exp(1))^2) z1 =0.2375(2)x=[2 1+2i;-0.45 5] x =2.0000 1.0000 + 2.0000i -0.4500 5.0000 z2=0.5*log(x+sqrt(1+x^2)) z2 =0.7114 - 0.0253i 0.8968 + 0.3658i 0.2139 + 0.9343i 1.1541 - 0.0044i (3)a=-3.0:0.1:3.0 a =Columns 1 through 5-3.0000 -2.9000 -2.8000 -2.7000 -2.6000 Columns 6 through 10-2.5000 -2.4000 -2.3000 -2.2000 -2.1000 Columns 11 through 15-2.0000 -1.9000 -1.8000 -1.7000 -1.6000 Columns 16 through 20-1.5000 -1.4000 -1.3000 -1.2000 -1.1000 Columns 21 through 25-1.0000 -0.9000 -0.8000 -0.7000 -0.6000 Columns 26 through 30-0.5000 -0.4000 -0.3000 -0.2000 -0.1000 Columns 31 through 350 0.1000 0.2000 0.3000 0.4000 Columns 36 through 400.5000 0.6000 0.7000 0.8000 0.9000 Columns 41 through 451.0000 1.1000 1.2000 1.3000 1.4000 Columns 46 through 501.5000 1.6000 1.7000 1.8000 1.9000 Columns 51 through 552.0000 2.1000 2.2000 2.3000 2.4000 Columns 56 through 602.5000 2.6000 2.7000 2.8000 2.9000 Column 613.0000z3=((exp(0.3*a)-exp(-0.3*a)).*sin(a+0.3))/2+log((a+0.3)/2) z3 =Columns 1 through 30.7388 + 3.1416i 0.7696 + 3.1416i 0.7871 + 3.1416i Columns 4 through 60.7913 + 3.1416i 0.7822 + 3.1416i 0.7602 + 3.1416i Columns 7 through 90.7254 + 3.1416i 0.6784 + 3.1416i 0.6196 + 3.1416i Columns 10 through 120.5496 + 3.1416i 0.4688 + 3.1416i 0.3780 + 3.1416i Columns 13 through 150.2775 + 3.1416i 0.1680 + 3.1416i 0.0497 + 3.1416i Columns 16 through 18-0.0771 + 3.1416i -0.2124 + 3.1416i -0.3566 + 3.1416i Columns 19 through 21-0.5104 + 3.1416i -0.6752 + 3.1416i -0.8536 + 3.1416i Columns 22 through 24-1.0497 + 3.1416i -1.2701 + 3.1416i -1.5271 + 3.1416i Columns 25 through 27-1.8436 + 3.1416i -2.2727 + 3.1416i -2.9837 + 3.1416i Columns 28 through 30-37.0245 -3.0017 -2.3085 Columns 31 through 33-1.8971 -1.5978 -1.3575 Columns 34 through 36-1.1531 -0.9723 -0.8083 Columns 37 through 39-0.6567 -0.5151 -0.3819 Columns 40 through 42-0.2561 -0.1374 -0.0255 Columns 43 through 450.0792 0.1766 0.2663 Columns 46 through 480.3478 0.4206 0.4841 Columns 49 through 510.5379 0.5815 0.6145 Columns 52 through 540.6366 0.6474 0.6470 Columns 55 through 570.6351 0.6119 0.5777 Columns 58 through 600.5327 0.4774 0.4126 Column 610.33880.7114 - 0.0253i 0.8968 + 0.3658i0.2139 + 0.9343i 1.1541 - 0.0044i(4)t=0:0.5:2.5;if t<1,z4=t.^2,elseif t<2,z4=t.^2-1,else z4=t.^2-2.*t+1,end; z4 =1.0000 0.2500 0 0.2500 1.00002.25003、已知:(1)A=[12 34 -4;34 7 87;3 65 7],B=[1 3 -1;2 0 3;3 -2 7],A+6*B,A =12 34 -434 7 873 65 7B =1 3 -12 0 33 -2 7ans =18 52 -1046 7 10521 53 49I=eye(3),I =1 0 00 1 00 0 1>> A-B+Ians =12 31 -332 8 840 67 1(2)A*Bans =68 44 62309 -72 596154 -5 241>> A.*Bans =12 102 468 0 2619 -130 49(3)A^3ans =37226 233824 48604247370 149188 60076678688 454142 118820>> A.^3ans =1728 39304 -6439304 343 65850327 274625 343(4)A/Bans =16.4000 -13.6000 7.600035.8000 -76.2000 50.200067.0000 -134.0000 68.0000>> B\Aans =109.4000 -131.2000 322.8000-53.0000 85.0000 -171.0000-61.6000 89.8000 -186.2000三、预习要求:利用所学知识,编写实验内容中1到3的相应程序,并写在预习报告上。
实验四、控制系统稳定性、时域和频域分析的MATLAB 实现一、实验目的1.熟悉MATLAB 的仿真及应用环境。
2.在MATLAB 的环境下研究控制系统稳定性。
3.使用频率分析法对系统进行相位超前、迟后、迟后-超前校正。
二、实验内容:1、若(3)(5)()(1)()(6)S S H S S S S α++=+++,当α分别取-3,-1,1,3,10时,判断系统的可控性与可观性,并求相应的状态空间模型。
当α=3时,以采样时间T=0.1s ,将系统离散化。
(1)当a=-3时num=conv([1 3],[1 5]);den1=conv(conv([1 1],[1 6]),[1-3]);[a,b,c,d]=tf2ss(num,den1),q1=obsv(a,c);n=rank(q1),m=ctrb(a,b);rank(m) a =-4 15 18 1 0 0 0 1 0 b = 1 0 0c =1 8 15 d = 0 n = 3 ans =3(2) 当a=-1时 num=conv([13],[15]);den1=conv(conv([11],[16]),[1-1]);[a,b,c,d]=tf2ss(num,den1),q1=obsv(a,c);n=rank(q1),m=ctrb(a,b);rank(m) a =-6 1 6 1 0 0 0 1 0 b = 1c =1 8 15d =n =3ans =3(3) 当a=1时num=conv([1 3],[1 5]);den1=conv(conv([1 1],[1 6]),[11]);[a,b,c,d]=tf2ss(num,den1),q1=obsv(a,c);n=rank(q1),m=ctrb(a,b);rank(m)a =-8 -13 -61 0 00 1 0b =1c =1 8 15d =n =3ans =3(4) 当a=3时num=conv([1 3],[1 5]);den1=conv(conv([1 1],[1 6]),[13]);[a,b,c,d]=tf2ss(num,den1),q1=obsv(a,c);n=rank(q1),m=ctrb(a,b);rank(m)a =-10 -27 -181 0 00 1 0b =1c =1 8 15d =n =2ans =3[abar,bbar,cbar,T,k] = obsvf(a,b,c)abar =-3.0000 16.2660 -27.4484-0.0000 -5.7310 9.67100.0000 0.1316 -1.2690bbar =-0.94350.3263-0.0587cbar =0.0000 -0.0000 -17.0294T =-0.9435 0.3145 -0.10480.3263 0.8249 -0.4617-0.0587 -0.4698 -0.8808k =1 1 0(5)a=10num=conv([1 3],[1 5]);den1=conv(conv([1 1],[1 6]),[110]);[a,b,c,d]=tf2ss(num,den1),q1=obsv(a,c);n=rank(q1),m=ctrb(a,b);rank(m)a =-17 -76 -601 0 00 1 0b =1c =1 8 15d =n =3ans =3hs=zpk(z,p,k,0.1)Zero/pole/gain:(z+3) (z+5)-----------------(z+1) (z+3) (z+6)Sampling time: 0.1 2、开环系统30(1)()(2)(3)(6)S H S S S S S +=++-,绘制系统nyquist 曲线并判断闭环系统的稳定性,绘制出闭环系统的单位冲激响应。
