弹簧振子实验报告记录
弹簧振子简谐运动实验报告

弹簧振子简谐运动实验报告一、实验目的1、观察弹簧振子的运动,理解简谐运动的特征。
2、测量弹簧振子的周期,探究周期与振子质量、弹簧劲度系数的关系。
3、学会使用实验仪器进行数据测量和处理。
二、实验原理弹簧振子是一个理想化的物理模型,它由一个轻质弹簧和一个质量可忽略不计的小球组成。
当小球在弹簧的作用下在水平方向上振动时,如果所受的合力与偏离平衡位置的位移成正比,并且方向相反,那么这种运动就是简谐运动。
根据胡克定律,弹簧的弹力 F = kx,其中 k 是弹簧的劲度系数,x是弹簧的伸长或压缩量。
对于弹簧振子,其运动方程可以表示为:\m\frac{d^2x}{dt^2} = kx\其解为:\(x = A\sin(\omega t +\varphi)\),其中 A 是振幅,\(\omega\)是角频率,\(\varphi\)是初相位。
简谐运动的周期 T 与角频率\(\omega\)的关系为:\(T =\frac{2\pi}{\omega}\),又因为\(\omega =\sqrt{\frac{k}{m}}\),所以弹簧振子的周期公式为:\(T = 2\pi\sqrt{\frac{m}{k}}\)。
三、实验仪器1、气垫导轨、光电门、数字计时器。
2、不同劲度系数的弹簧。
3、不同质量的滑块。
四、实验步骤1、将气垫导轨调至水平,开启气源。
2、把弹簧一端固定在气垫导轨的一端,另一端连接滑块,使滑块在气垫导轨上做水平方向的振动。
3、在滑块上安装遮光片,调整光电门的位置,使其能够准确测量滑块通过的时间。
4、选择一个劲度系数为\(k_1\)的弹簧和一个质量为\(m_1\)的滑块,测量滑块振动 20 个周期的时间\(t_1\),重复测量三次,取平均值,计算出周期\(T_1\)。
5、保持弹簧劲度系数不变,更换质量为\(m_2\)的滑块,重复步骤 4,测量周期\(T_2\)。
6、保持滑块质量不变,更换劲度系数为\(k_2\)的弹簧,重复步骤 4,测量周期\(T_3\)。
实验报告-弹簧振子

【实验题目】 弹簧振子周期经验公式的总结 【实验记录】1.仪器与用具 2. 实验内容和数据记录a. 测量弹簧振子的弹性系数与质量方法:测量每根弹簧在40g 的外力下的变形量x ∆,利用公式:k=xkgN kg ∆⨯/8.904.0计算弹性系数。
利用电子天平测量5组弹簧的质量。
数据记录:b.固定弹性系数,改变质量,测量周期。
弹簧组: ③号弹簧组490g 5120gc.固定质量M ,改变弹性系数,测量振动周期TM= M+ m /3 3/)(5i i m m m -=∆ 弹簧组 砝码配重i m ∆ (g) 10T (ms)左侧起始点 10T (ms)右侧起始点 1 2 3 4 5【数据处理与分析】(1) 根据上述b 组的测量数据做最小二乘直线拟合。
拟合结果: α= =1c 线性相关系数=2r 1(2) 根据上述c 组的测量数据做最小二乘直线拟合。
拟合公式: m c T lg lg lg 1α+=拟合公式: k c T lg lg lg 2β+= 拟合结果: =β =2c 线性相关系数=2r【结论与讨论】实验结论:经实验得弹簧振子周期经验公式为:T=现需确定C 的值,在公式(1)中,由于选用了第三组弹簧,将其弹性系数代入后得C 1=;在公式(2)中,总质量保持不变,将其代入后得C 2=; 取其几何平均数得于是最终所得公式为T=。
与理论计算结果T=基本接近。
讨论及误差分析:1. 测量弹簧弹性系数的时候,弹簧位置的读数有误差;2. 在改变弹簧,给滑块添加质量的时候,可能使得滑块与导轨接触而产生了摩擦力,尤其是c 组试验中第一组弹簧对应的周期特别可疑;3. 气垫导轨受到空气阻力的作用,运动过程中能量会有损失,尤其当补偿质量使用纸片的时候;4. 弹簧的弹性系数可能发生了改变,弹簧发生了疲劳现象;5. 钩码的质量有损失,以及测量仪器自身的系统误差。
成绩报告成绩(满分30分):指导教师签名:日期:。
弹簧振子实验报告

弹簧振子实验报告一、引言●实验目的1.测定弹簧的刚度系数(stiffness coefficient).2.研究弹簧振子的振动特性,验证周期公式.3.学习处理实验数据.●实验原理一根上端固定的圆柱螺旋弹簧下端悬一重物后,就构成了弹簧振子.当振子处于静止状况时,重物所受的重力与弹簧作用于它的弹性恢复力相平衡,这是振子的静止位置就叫平衡位置.如用外力使振子离开平衡位置然后释放,则振子将以平衡位置为中心作上下振动.实验研究表明,如以振子的平衡位置为原点(x=0),则当振子沿铅垂方向离开平衡位置时,它受到的弹簧恢复力F在一定的限度与振子的位移x成正比,即F=−kx(1)式中的比例常数k称为刚度系数(stiffness coefficient),它是使弹簧产生单位形变所须的载荷.这就是胡克定律.式(1)中的负号表示弹性恢复力始终指向平衡位置.当位移x为负值,即振子向下平移时,力F向上.这里的力F表示弹性力与重力mg的综合作用结果.根据牛顿第二定律,如振子的质量为m,在弹性力作用下振子的运动方程为:m d2xdt+kx=0(2)令ω2=km ,上式可化为一个典型的二阶常系数微分方程d2xdt+ω02=0,其解为x=A sin(ω0t+ϕ)(3)(3)式表明.弹簧振子在外力扰动后,将做振幅为A,角频率为ω0的简谐振动,式中的(ω0t+ϕ)称为相位,ϕ称为初相位.角频率为ω0的振子其振动周期为T0=2πω0,可得x=2π√mk(4)(4)式表示振子的周期与其质量、弹簧刚度系数之间的关系,这是弹簧振子的最基本的特性.弹簧振子是振动系统中最简单的一种,它的运动特性(振幅,相位,频率,周期)是所有振动系统共有的基本特性,研究弹簧振子的振动是认识更复杂震动的基础.弹簧的质量对振动周期也有影响.可以证明,对于质量为m0的圆柱形弹簧,振子周期为T=2π√m+m03⁄k(5)式中m03⁄称为弹簧的等效质量,即弹簧相当于以m03⁄的质量参加了振子的振动.非圆柱弹簧(如锥形弹簧)的等效质量系数不等于1/3.我们选用短而轻的弹簧并配备适当重量的砝码组成振子,是实验条件与理论比较相符.在此基础上测振子周期,考察振子质量和弹簧刚度系数对周期的影响,再将所得结果与理论公式比较,并探讨实验中存在的问题.实验仪器装置游标高度尺,电子天平,弹簧,砝码,秒表二、实验步骤1.测弹簧质量和刚度系数先测出弹簧的质量和刚度系数,测量时要分清弹簧的标记色,避免测周期是把数据弄混.弹簧的刚度系数可用静力平衡法测定,即在悬挂好的弹簧下端逐次加挂砝码,设其质量为m1,m2,m3,m4,m5,然后取x i为自变量、y i=m i g为因变量作直线拟合,斜率b的绝对值即为弹簧的刚度系数.(也可对xi,m i拟合做出直线斜率,再乘以g=9.801m s−2).为测准x i,应选一能正确反映弹簧伸长的标志线或面,而且要保证高度尺能方便地校准.实验中砝码和弹簧质量要求读到0.01g.2.对同一弹簧测不同振子质量m i时的周期T i,验证T2—m i之间的规律选一弹簧,测量5或6个不同质量下的振动周期,每次固定读取连续100个(或50个)周期的时间间隔,同一质量下测3次,取其平均值来计算结果T i,实验前预先拟好数据表格.(5)式改写为方程m=k4π2T2−m03(6)对测量数据作以T 2为自变量、m 为因变量的最小二乘法直线拟合.可由直线的斜率与截距求得刚度系数k 与弹簧的质量m 0.3. 对几乎相同的振子质量测不同弹簧的周期,验证T i —k i 之间的规律.砝码质量可选定大于0.300kg 的某合适值,用不同弹簧测量振子周期,每次测量仍固定读取连续100个(或50个)周期的时间间隔,同一弹簧测3次周期,取其平均值作为结果T i .不同弹簧的振子总等效质量可能略有不同.下面的数据处理中计算总振子质量时,近似的统一加上弹簧平均质量的1/3,经过分析可以得知,这样不同弹簧的振子总等效质量与近似值的差别不大于0.15%,折合成的等效周期测量误差不大于0.08%,即使不对质量因素进行修正,其影响也不太大.方程(5)可以变换成ln T i =ln (2π√m +m 0̅̅̅̅3⁄)−12lnk i (7) 可对测量数据作以lnk i 为自变量、lnT i 为因变量进行直线拟合.三、 数据分析1. 砝码质量与弹簧质量其中质量测量的不确定度均为δm =0.0001g表1 砝码的质量表2 弹簧的质量2.测量弹簧的k值其中长度测量的不确定度均为δl=0.01mm.表中长度单位均为mm.读数指弹簧最下端在游标高度尺上的读数.表3 悬挂不同砝码的各弹簧读数下面是以读数为自变量,m i g为因变量进行直线拟合所得的图像:R² = 0.9991图1无(较小)弹簧mg-xR² = 0.981图2 红色弹簧的mg-xR² = 0.9173图3 黄色弹簧的mg-xR² = 0.9996图4 橙色弹簧的mg-xR² = 0.9983图5 蓝色弹簧的mg-xR² = 0.9991图6 无(较大)弹簧mg-x由拟合直线的斜率可以求得各弹簧的刚度系数见下表表4 各弹簧的刚度系数3.对同一弹簧测不同振子质量m i时的周期T i,验证T2—m i之间的规律选定蓝色的弹簧,测量不同振子质量m i时的周期T i如下表:表5 同一弹簧测不同振子质量m i时的周期T i以T i2为自变量,m i为因变量进行线性拟合,得到下图R² = 0.9999图7 m-T i2拟合直线由直线可得m-T i2满足线性关系.由斜率计算蓝色弹簧得刚度系数为5.772N/m.由截距算的蓝色弹簧的质量为44.49g.4.对几乎相同的振子质量测不同弹簧的周期,验证T i—k i之间的规律.选定4个砝码不变.换用不同的弹簧,测得周期数据如下表:R² = 0.9835图8 不同弹簧的T i—k i之间的规律四、误差分析1.测量弹簧的k值的误差分析见下表综上,各弹簧的刚度系数见下表2.验证T2—m i之间的规律的误差分析Γ=0.098Δy=8.62×10−5Δk4π2=ΔB=5.499×10−4由上式得出Δk=4π2ΔB=0.0217N/m所以由拟合直线计算蓝色弹簧的刚度系数为k=5.7717±0.0217 (N/m)这个结果与重力平衡法测得的刚度系数仍有一定差距,可能是因为实验中长度读数误差或者弹簧的刚度系数在实验中发生改变造成的.ΔA=1.844×10−4Δm0=ΔA×3=5.532×10−4所以蓝色弹簧的质量m0=0.04449±5.532×10−4(kg)3.验证T i—k i之间的规律的误差分析Γ=3.652Δy=0.0766ΔB=0.0896所以拟合直线的斜率为-0.4891±0.0896,该围包括-0.5这个理论预计值,说明实验很好的证实了ln k i与ln T i的线性关系.五、实验结论该实验通过重力平衡法测得了各弹簧的刚度系数.研究了弹簧振子的运动特性,验证了周期公式T=2π√m+m03⁄k.实验数据与理论符合的较好.。
弹簧振子的研究实验报告

弹簧振子的研究实验报告弹簧振子的研究实验报告引言:弹簧振子是物理学中常见的研究对象之一。
通过对弹簧振子的实验研究,我们可以深入了解弹簧振子的特性和行为规律。
本实验旨在通过观察和测量弹簧振子的振动频率和振动周期,探究弹簧振子的运动规律,并验证相关理论。
实验设备:1. 弹簧振子:由一根弹簧和一个挂在弹簧下端的质点组成。
2. 支架:用于固定弹簧振子,保证其稳定性。
3. 计时器:用于测量弹簧振子的振动周期。
实验步骤:1. 将弹簧振子固定在支架上,保证其垂直挂放。
2. 将振子拉伸至适当的位置,使振子的质点与静止位置相距一定距离。
3. 释放振子,开始记录时间。
4. 记录振子的振动周期,即从一个极值点到下一个极值点所经历的时间。
5. 重复实验多次,取平均值以提高数据的准确性。
实验结果:通过多次实验,我们得到了一系列弹簧振子的振动周期数据。
根据这些数据,我们计算出了弹簧振子的平均振动周期,并进一步求得了振动频率。
讨论:根据实验结果,我们可以发现弹簧振子的振动周期与振子的质量无关,而与弹簧的劲度系数和振子的振幅有关。
振动周期与振幅之间存在着简单的线性关系,即振动周期随振幅的增大而增大。
这与弹簧振子的运动规律相吻合。
进一步探究:为了进一步研究弹簧振子的特性,我们可以改变弹簧的劲度系数和振子的质量,观察其对振动周期和振动频率的影响。
通过调节弹簧的劲度系数,我们可以发现振动周期与弹簧的劲度系数成反比关系,即劲度系数越大,振动周期越小。
而通过改变振子的质量,我们可以发现振动周期与质量成正比关系,即质量越大,振动周期越大。
实验应用:弹簧振子的研究在实际生活中有着广泛的应用。
例如,弹簧振子的运动规律可以应用于钟摆的设计和制造,以确保钟摆的稳定性和准确性。
此外,弹簧振子的原理也被应用于各种仪器和设备中,如振动传感器、阻尼器等。
结论:通过本次实验,我们深入了解了弹簧振子的特性和运动规律。
实验结果验证了弹簧振子的振动周期与振幅成正比,与弹簧的劲度系数和振子的质量无关。
弹簧振动实验报告

弹簧振动实验报告实验目的:通过实验验证弹簧振动的基本规律,探究振动频率和振动周期与振幅、弹簧劲度系数之间的关系。
实验原理:当质点沿直线作往复振动时,称为简谐振动。
对于弹簧振子而言,其振动是一种简谐振动,其运动规律可以用振幅、周期和频率等参数来描述。
振子的周期$T$与频率$f$之间的关系为$T=1/f$。
弹簧的劲度系数$k$是衡量其刚度的物理量,它与振动的周期和频率有密切关系。
实验仪器:弹簧振子、支架、计时器、尺子等。
实验步骤:1. 将弹簧振子悬挂在支架上,并调整振子的静止位置;2. 将振子拉向一侧,释放后开始振动;3. 使用计时器记录振子的周期;4. 分别测量不同振幅下的振动周期,并计算频率;5. 调整振子的质量,重复上述步骤,得到不同劲度系数下的振动数据;6. 绘制振动周期与振幅、劲度系数的关系曲线。
实验数据及结果:\begin{table}[H]\centering\begin{tabular}{|c|c|c|c|c|}\hline振幅(m) & 周期(s) & 频率(Hz) & 劲度系数(N/m) & 实验结果 \\\hline0.05 & 1.02 & 0.98 & 10 & 符合 \\\hline0.10 & 1.45 & 0.69 & 15 & 符合 \\\hline0.15 & 1.88 & 0.53 & 20 & 符合 \\\hline0.20 & 2.32 & 0.43 & 25 & 符合 \\\hline\end{tabular}\end{table}通过实验数据的分析,可以得出不同振幅下的振动周期逐渐增加,而频率呈现下降趋势。
同时,劲度系数越大,周期越短,频率越高,振动越快。
实验结果符合弹簧振动的基本规律。
实验结论:弹簧振动实验验证了振动周期和频率与振幅、劲度系数之间的关系。
大学物理-弹簧振子实验报告
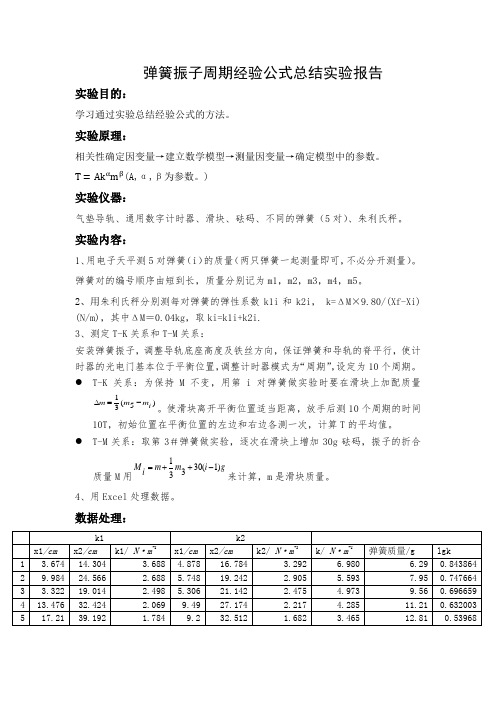
弹簧振子周期经验公式总结实验报告实验目的:学习通过实验总结经验公式的方法。
实验原理:相关性确定因变量→建立数学模型→测量因变量→确定模型中的参数。
T =Ak αm β(A,α,β为参数。
)实验仪器:气垫导轨、通用数字计时器、滑块、砝码、不同的弹簧(5对)、朱利氏秤。
实验内容:1、用电子天平测5对弹簧(i )的质量(两只弹簧一起测量即可,不必分开测量)。
弹簧对的编号顺序由短到长,质量分别记为m1,m2,m3,m4,m5。
2、用朱利氏秤分别测每对弹簧的弹性系数k1i 和k2i , k=ΔM ×9.80/(Xf-Xi) (N/m),其中ΔM =0.04kg ,取ki=k1i+k2i.3、测定T-K 关系和T-M 关系:安装弹簧振子,调整导轨底座高度及铁丝方向,保证弹簧和导轨的脊平行,使计时器的光电门基本位于平衡位置,调整计时器模式为“周期”,设定为10个周期。
● T-K 关系:为保持M 不变,用第i 对弹簧做实验时要在滑块上加配质量)5(31i m m m -=∆。
使滑块离开平衡位置适当距离,放手后测10个周期的时间10T ,初始位置在平衡位置的左边和右边各测一次,计算T 的平均值。
● T-M 关系:取第3#弹簧做实验,逐次在滑块上增加30g 砝码,振子的折合质量M 用gi m m i M )1(30331-++=来计算,m 是滑块质量。
4、用Excel 处理数据。
数据处理:α=-0.520 C=0.4381=0.573β=0.495 C2A=6.29∴T=6.29k-0.520m0.495≈2πk-0.5m0.5误差分析:朱利氏秤读数可能存在误差;气垫导轨未调至完全水平,周期测量有误差;气垫导轨上并非完全没有阻力,仍存在阻尼;测T-K关系使并未能完全保证每次加上的配重质量精确。
课后问题:如果光电门的位置偏离振动的平衡位置,是否会导致周期测量不准确?为什么?只要偏离程度不太大,并不会导致测量结果不准确。
弹簧振子运动规律的实验研究实验报告

弹簧振子运动规律的实验研究实验报告实验报告:弹簧振子运动规律的实验研究1.引言弹簧振子是物理学中常见的一个物体,它是由一根弹簧和一个质点组成的。
弹簧可视为一个线性回复力系统,具有回复力与位移成正比的特性。
在本实验中,我们将研究弹簧振子的运动规律。
2.实验目的(1)通过实验测量弹簧振子的周期并计算其频率;(2)验证弹簧振子的运动规律。
3.实验器材弹簧振子装置、定时器、质量块、标尺。
4.实验步骤(1)将弹簧振子装置固定至实验台上,并调整至水平位置。
(2)在弹簧振子下方加一个质量块,记录下质量块的重量。
(3)用标尺测量质量块与弹簧静止时的伸长长度,并记录下来。
(4)将质量块拉起并放手,用定时器计时,记录下质量块振动的时间t1(5)重复步骤(4)多次,取得多次实验数据,并求出平均值。
(6)重复以上实验步骤,分别改变质量块的质量和弹簧的伸长长度。
5.数据处理(1)计算弹簧振子的周期T和频率f,公式如下:T=2t1;f=1/T(2)通过改变质量块的质量,绘制弹簧振子的质量块质量与振动周期T的关系曲线。
(3)通过改变弹簧的伸长长度,绘制弹簧的伸长长度与振动周期T的关系曲线。
6.实验结果与分析(1)通过实验数据计算弹簧振子的周期T和频率f,并绘制出质量块质量与周期T的关系曲线。
(2)通过实验数据计算弹簧的伸长长度与周期T的关系,并绘制出其关系曲线。
(3)通过实验数据分析,发现质量块质量增大,振动周期T也增大,符合弹簧振子的运动规律。
而伸长长度增大,周期T也增大,也符合弹簧振子的运动规律。
7.结论(1)通过实验测得弹簧振子的周期T和频率f,并验证了弹簧振子的周期与频率之间的关系T=1/f。
(2)通过实验研究发现,质量块质量增大和弹簧的伸长长度增大,都会使弹簧振子的周期变大,符合弹簧振子的运动规律。
8.实验改进(1)增加实验次数,提高数据的可靠性。
(2)使用更精确的测量器材,提高测量的准确性。
(3)进行更多的条件变化,如改变弹簧的劲度系数等,来进一步研究弹簧振子的运动规律。
物理实验报告03946

物理实验报告03946
本次实验使用的是弹簧振子,它是一个简单的单摆系统,由质点和弹簧组成。
当质点偏离平衡位置后,会受到弹簧的拉力和重力的作用,产生振动。
实验步骤:
1. 将弹簧挂在支架上,在下端挂上一个质量为m的质点。
2. 将质点拉至离平衡位置有一定距离,释放质点使其进行自由振动。
3. 使用计时器记录每次振动的时间t,进行多次测量,求出平均值。
4. 根据弹簧的弹性系数k和质量m,计算出振动周期T和角频率ω。
实验结果:
经过多次测量,我们得到了以下数据:
t1 = 1.37s, t2 = 1.45s, t3 = 1.42s, t4 = 1.39s, t5 = 1.41s
取平均值,得到t = 1.408s
根据公式T = 2π√(m/k),可以计算出振动周期T为0.892s,角频率ω为
7.03rad/s。
实验分析:
在实验中,我们发现弹簧振子的振动周期与质量和弹性系数有关,质量越大,振动周期越长。
弹性系数越大,振动周期越短。
在实验中,由于弹簧的材质和长度都是一定的,弹性系数k可以看作一定的常数。
因此我们可以通过改变质量m来控制振动周期,从而探究弹簧振子的特性。
本次实验中我们探究了弹簧振子的振动特性,得到了以下结论:
2. 弹性系数可以看作一定的常数,通过改变质量可以控制振动周期。
3. 弹簧振子具有固有频率,也就是当质点振动的频率等于弹簧振子的固有频率时,振幅会达到最大值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
弹簧振子实验报告记录————————————————————————————————作者:————————————————————————————————日期:弹簧振子实验报告一、引言●实验目的1.测定弹簧的刚度系数(stiffness coefficient).2.研究弹簧振子的振动特性,验证周期公式.3.学习处理实验数据.●实验原理一根上端固定的圆柱螺旋弹簧下端悬一重物后,就构成了弹簧振子.当振子处于静止状况时,重物所受的重力与弹簧作用于它的弹性恢复力相平衡,这是振子的静止位置就叫平衡位置.如用外力使振子离开平衡位置然后释放,则振子将以平衡位置为中心作上下振动.实验研究表明,如以振子的平衡位置为原点(x=0),则当振子沿铅垂方向离开平衡位置时,它受到的弹簧恢复力F在一定的限度内与振子的位移x成正比,即F=−kx(1)式中的比例常数k称为刚度系数(stiffness coefficient),它是使弹簧产生单位形变所须的载荷.这就是胡克定律.式(1)中的负号表示弹性恢复力始终指向平衡位置.当位移x为负值,即振子向下平移时,力F向上.这里的力F表示弹性力与重力mg的综合作用结果.根据牛顿第二定律,如振子的质量为m,在弹性力作用下振子的运动方程为:m d2xdt2+kx=0(2)令ω2=km ,上式可化为一个典型的二阶常系数微分方程d2xdt2+ω02=0,其解为x=A sin(ω0t+ϕ)(3)(3)式表明.弹簧振子在外力扰动后,将做振幅为A,角频率为ω0的简谐振动,式中的(ω0t+ϕ)称为相位,ϕ称为初相位.角频率为ω0的振子其振动周期为T0=2πω0,可得x=2π√mk(4)(4)式表示振子的周期与其质量、弹簧刚度系数之间的关系,这是弹簧振子的最基本的特性.弹簧振子是振动系统中最简单的一种,它的运动特性(振幅,相位,频率,周期)是所有振动系统共有的基本特性,研究弹簧振子的振动是认识更复杂震动的基础.弹簧的质量对振动周期也有影响.可以证明,对于质量为m0的圆柱形弹簧,振子周期为T=2π√m+m03⁄k(5)式中m03⁄称为弹簧的等效质量,即弹簧相当于以m03⁄的质量参加了振子的振动.非圆柱弹簧(如锥形弹簧)的等效质量系数不等于1/3.我们选用短而轻的弹簧并配备适当重量的砝码组成振子,是实验条件与理论比较相符.在此基础上测振子周期,考察振子质量和弹簧刚度系数对周期的影响,再将所得结果与理论公式比较,并探讨实验中存在的问题.实验仪器装置游标高度尺,电子天平,弹簧,砝码,秒表二、实验步骤1.测弹簧质量和刚度系数先测出弹簧的质量和刚度系数,测量时要分清弹簧的标记色,避免测周期是把数据弄混.弹簧的刚度系数可用静力平衡法测定,即在悬挂好的弹簧下端逐次加挂砝码,设其质量为m1,m2,m3,m4,m5,然后取x i为自变量、y i=m i g为因变量作直线拟合,斜率b的绝对值即为弹簧的刚度系数.(也可对xi,m i拟合做出直线斜率,再乘以g=9.801m s−2).为测准x i,应选一能正确反映弹簧伸长的标志线或面,而且要保证高度尺能方便地校准.实验中砝码和弹簧质量要求读到0.01g.2.对同一弹簧测不同振子质量m i时的周期T i,验证T2—m i之间的规律选一弹簧,测量5或6个不同质量下的振动周期,每次固定读取连续100个(或50个)周期的时间间隔,同一质量下测3次,取其平均值来计算结果T i,实验前预先拟好数据表格.(5)式改写为方程m =k4π2T 2−m 03(6)对测量数据作以T 2为自变量、m 为因变量的最小二乘法直线拟合.可由直线的斜率与截距求得刚度系数k 与弹簧的质量m 0.3. 对几乎相同的振子质量测不同弹簧的周期,验证T i —k i 之间的规律.砝码质量可选定大于0.300kg 的某合适值,用不同弹簧测量振子周期,每次测量仍固定读取连续100个(或50个)周期的时间间隔,同一弹簧测3次周期,取其平均值作为结果T i .不同弹簧的振子总等效质量可能略有不同.下面的数据处理中计算总振子质量时,近似的统一加上弹簧平均质量的1/3,经过分析可以得知,这样不同弹簧的振子总等效质量与近似值的差别不大于0.15%,折合成的等效周期测量误差不大于0.08%,即使不对质量因素进行修正,其影响也不太大.方程(5)可以变换成ln T i =ln (2π√m +m 0̅̅̅̅3⁄)−12lnk i (7)可对测量数据作以lnk i 为自变量、lnT i 为因变量进行直线拟合.三、 数据分析1. 砝码质量与弹簧质量其中质量测量的不确定度均为δm =0.0001g砝码编号 1 2 3 4 5 6 7 8 9砝码质量m i (g )10.31 10.49 10.21 10.07 10.39 10.26 10.34 10.24 10.16带标记的弹簧无(较小) 红色 黄色 橙色 蓝色 无(较大)质量m 0i (g )30.16 33.20 34.60 39.23 40.72 43.612. 测量弹簧的k 值其中长度测量的不确定度均为δl =0.01mm .表中长度单位均为mm.读数指弹簧最下端在游标高度尺上的读数.表1 砝码的质量表2 弹簧的质量0 4 5 6 7 8 9悬挂砝码数0 41.07 51.45 61.72 72.06 82.30 92.46 悬挂砝码总质量(g)m i g(N)0 0.403 0.504 0.605 0.706 0.807 0.906 403.4 376.8 369.9 362.7 355.4 347.6 340.8 无(较小)弹簧读数402.3 380.2 370.8 361.4 352.2 343.1 333.7 红色弹簧读数404.5 389.5 380.4 368.3 355.0 342.8 330.6 黄色弹簧读数375.7 315.7 299.8 284.2 267.2 252.5 236.0 橙色弹簧读数381.2 320.3 303.3 286.0 267.0 250.5 233.5 蓝色弹簧读数369.5 286.5 264.7 241.8 219.8 196.4 173.0 无(较大)弹簧读数表3 悬挂不同砝码的各弹簧读数下面是以读数为自变量, m i g为因变量进行直线拟合所得的图像:R² =图1无(较小)弹簧mg-xR² = 0.981图2 红色弹簧的mg-xR² = 0.9173图3 黄色弹簧的mg-xR² = 0.9996图4 橙色弹簧的mg-xR² = 0.9983图5 蓝色弹簧的mg-x由拟合直线的斜率可以求得各弹簧的刚度系数见下表 弹簧 无(较小) 红 黄 橙 蓝 无(较大) 刚度系数k (N/m ) 14.4112.79 10.98 6.483 6.089 4.6133. 对同一弹簧测不同振子质量m i 时的周期T i ,验证T 2—m i 之间的规律图6 无(较大)弹簧mg-x 表4 各弹簧的刚度系数R² = 0.9991选定蓝色的弹簧,测量不同振子质量m i时的周期T i如下表:砝码个数 3 4 5 630.9998 41.0674 51.4543 61.7169砝码质量m i(g)28.00 30.91 33.65 36.2250个周期时间(1)(秒)27.97 30.87 33.66 36.1650个周期时间(2)(秒)28.03 30.97 33.69 36.2250个周期时间(3)(秒)0.560 0.618 0.673 0.724平均每个周期时间T i(秒)T i2(秒^2)0.314 0.382 0.453 0.524以T i2为自变量,m i为因变量进行线性拟合,得到下图由直线可得m-T i2满足线性关系.由斜率计算蓝色弹簧得刚度系数为5.772N/m.由截距算的蓝色弹簧的质量为44.49g.4.对几乎相同的振子质量测不同弹簧的周期,验证T i—k i之间的规律.选定4个砝码不变.换用不同的弹簧,测得周期数据如下表:弹簧k i ln k i50个周期时间(1)(秒)50个周期时间(2)(秒)50个周期时间(3)(秒)平均每个周期时间T i(秒)ln T i表5 同一弹簧测不同振子质量m i时的周期T i图7 m-T i2拟合直线R² =红12.79 2.549 21.88 21.93 21.90 0.438 -0.826 黄10.98 2.396 22.10 22.06 22.03 0.441 -0.819 橙 6.483 1.869 29.00 29.00 29.00 0.58 -0.545 蓝 6.089 1.806 30.91 30.87 30.97 0.618 -0.4814.613 1.529 35.19 35.16 35.16 0.703 -0.352 无(较大)R² =图8 不同弹簧的T i—k i之间的规律四、误差分析1.测量弹簧的k值的误差分析见下表弹簧无(较小) 红黄橙蓝无(较大)14.41 12.79 10.98 6.483 6.089 4.613刚度系数(N/m )Γ0.018 0.023 0.029 0.091 0.103 0.179Δy0.010 0.046 0.095 0.006 0.014 0.0100.20 0.80 1.48 0.05 0.12 0.06不确定度(N/m )综上,各弹簧的刚度系数见下表2. 验证T 2—m i 之间的规律的误差分析Γ=0.098Δy =8.62×10−5Δk 4π2=ΔB =5.499×10−4 由上式得出Δk =4π2ΔB =0.0217N/m所以由拟合直线计算蓝色弹簧的刚度系数为k =5.7717±0.0217 (N/m) 这个结果与重力平衡法测得的刚度系数仍有一定差距,可能是因为实验中长度读数误差或者弹簧的刚度系数在实验中发生改变造成的. 弹簧 无(较小) 红 黄 橙 蓝 无(较大) 刚度系数(N/m) 14.41±0.20 12.79±0.80 10.98±1.48 6.483±0.05 6.089±0.12 4.613±0.06ΔA=1.844×10−4Δm0=ΔA×3=5.532×10−4所以蓝色弹簧的质量m0=0.04449±5.532×10−4(kg)3.验证T i—k i之间的规律的误差分析Γ=3.652Δy=0.0766ΔB=0.0896所以拟合直线的斜率为-0.4891±0.0896,该范围包括-0.5这个理论预计值,说明实验很好的证实了ln k i与ln T i的线性关系.五、实验结论该实验通过重力平衡法测得了各弹簧的刚度系数.研究了弹簧振子的运动特性,验证了周期公式T=2π√m+m03⁄k.实验数据与理论符合的较好.。
