数据模型与决策案例一
数据模型与决策R.C. Coleman案例
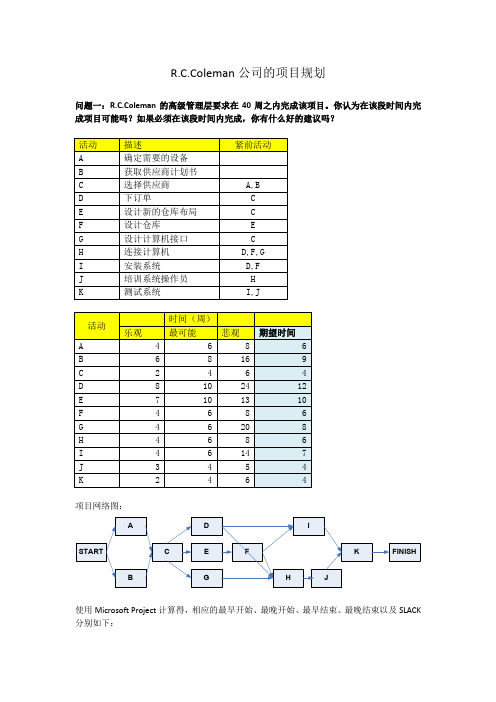
R.C.Coleman公司的项目规划问题一:R.C.Coleman的高级管理层要求在40周之内完成该项目。
你认为在该段时间内完成项目可能吗?如果必须在该段时间内完成,你有什么好的建议吗?项目网络图:使用Microsoft Project计算得,相应的最早开始、最晚开始、最早结束、最晚结束以及SLACK 分别如下:其关键路径为:B-C-E-F-H-J-K,项目完成时间为43周,即在40周内是无法完成该项目的。
分别计算各个活动的方差得:从而项目的完成时间的方差可以表示为:σ2=5.65从而σ=2.38当40<=T<=43时,Z=(43-40)/2.38=1.26通过查表得:Pr(40<=T<=43)=0.3962Pr(T<=40)=0.5-0.3962=0.103=10.38%即在40周内项目完工的可能性只有10.38%,几率很低,完成不了。
问题二:管理人员要求缩减活动时间以使在40周之内完成该项目的可能性达到80%。
如果项目完成时间的偏差和(1)问一样,应该缩减多少项目期望完成时间以使在40周内完成该项目的可能性达到80%?如图,在40周内完成的概率达到80%概率的情况:Pr(T<=40) = 0.8Pr(x<=T<=40) = 0.8-0.5 = 0.3查表的:z(x<=T<=40) = 0.84即(40-x)/2.38 = 0.84从而x=38周,即项目完成时间需要缩短到38周以使得在40周内完成的可能性达到80%。
问题三:将期望活动时间作为正常的时间,利用如下的紧缩信息,制定仓库扩展项目活动的紧缩决策和修改后的活动时间表。
假设Xi代表活动i的完成时间,Yi代表活动i的紧缩时间,其中i=A、B、C、D、E、F、G、H、I、J、K。
构建线性模型如下:求解得到如下的紧缩决策和修改后的活动时间表:。
数据,模型与决策-运用电子表格建模与案例研究,pdf

数据,模型与决策:运用电子表格建模与案例研究,pdf篇一:数据模型与决策2002年旅游产业企业及收入分析一、研究的目的要求旅游业在社会经济的持续发展中有着重要的作用。
旅游者合理的旅游消费模式和适度的旅游消费规模有利于经济持续健康的增长,而且这也是人民生活水平的具体体现。
改革开放以来随着中国经济的快速发展,人民生活水平不断提高,居民的旅游消费水平也不断增长。
但是在看到这个整体趋势的同时,还应看到全国各地区旅游经济发展速度不同,居民旅游消费水平也有明显差异。
例如,2002年全国旅游业全员劳动生产率为51.7万元/人, 最低的青海省仅为11.9万元,最高的北京市达110.7元,上海是黑龙江的9.3倍。
为了研究全国旅游业全员劳动生产率水平及其变动的原因,需要作具体的分析。
影响各地区旅游业全员劳动生产率有明显差异的因素可能很多,例如,旅游资源开发水平、宣传力度、交通便利程度、旅游服务质量、旅游者兴趣爱好、购物环境等等都可能对旅游业全员劳动生产率有影响。
为了分析什么是影响各地区旅游业全员劳动生产率有明显差异的最主要因素,并分析影响因素与旅游业全员劳动生产率的数量关系,可以建立相应的计量经济模型去研究。
二、模型设定我们研究的对象是各地区旅游业全员劳动生产率的差异。
旅游业全员劳动生产率可分为境外旅游业全员劳动生产率和境内旅游业全员劳动生产率,由于各地区的境外与境内旅游者比例及兴趣爱好有较大差异,最具有直接对比可比性的是总的旅游业全员劳动生产率。
而且,由于各地区从业人员数量和旅游资源总量不同,只能用“旅游业全员劳动生产率”来比较,而这正是可从统计年鉴中获得数据的变量。
所以模型的被解释变量Y选定为“旅游业全员劳动生产率”。
因为研究的目的是各地区旅游业全员劳动生产率的差异,并不是旅游业全员劳动生产率在不同时间的变动,所以应选择同一时期各地区旅游业全员劳动生产率来建立模型。
因此建立的是2002年截面数据模型。
影响各地区旅游业全员劳动生产率有明显差异的因素有多种,但从理论和经验分析,最主要的影响因素应是旅行社数,其他因素虽然对旅游业全员劳动生产率也有影响,但有的不易取得数据,如“宣传力度”和“旅游者兴趣爱好”;有的与旅行社数可能高度相关,如“旅游服务质量”、“旅游资源开发水平”;还有的因素在运用截面数据时在地区间的差异并不大,如“购物环境”、“交通便利程度”。
数据模型与决策分析案例

数据模型与决策分析案例一、问题提出美国R银行最近赢得了一份合同,为宾夕法尼亚的众多公司修建一个服务区,使得他们可以开启网上交易,便捷各自的生活。
R银行负责区域银行卡的网上注册,数据维护与测试。
为了完成这项工作,美国R银行的负责人兼总经理Bob xx估计,区域内所有员工银行卡的注册与网上注册所需要的总工期大约需要4个月,并且完成这项庞大的任务需要许多的云服务器支持,从各项数据,可以得知,从第1个月到第4个月需要的云服务器分别为10、12、14、8台云服务器。
虽然说到目前为止美国R银行已经有20台云服务器,但大部分的台云服务器都有任务,都要支持运行维护已经注册的人员的银行数据,因此,必须从从P xx云服务器租赁公司租借部分的云服务器。
并且Bob估计,虽然说本公司这些云服务器有其他的任务,但每个月任然有部分可以抽调出来供这一份项目使用,第1个月有1台云服务器可以用于服务区的网上注册,数据维护与测试任务,第2个月有2台云服务器可以用于服务区任务,第3个月有3台云服务器可以用于服务区任务,第4个月有1台云服务器可以用于服务区任务。
因此为了完成任务,美国R银行还需要租借更多的云服务器来完成这一份合同。
从P xx云服务器公司长期租用云服务器的费用是每台云服务器每月600美元。
云服务器的坐守监视工作人员的工资是每小时20美元,每台云服务器每天消耗流量电量等数据网络方面花费为100美元。
所有的云服务器维修费用由Pxx云服务器公司承担。
根据美国R银行工作计划,美国R银行每天工作8小时,每周5天,每月工作4周。
Bob认为现在的情况下,美国R银行如果长期租赁云服务器是不明智的。
在与P xx云服务器公司对短期租赁合同进行讨论后,Bob了解到他可以获得1-4个月的短期租赁。
短期云服务器租赁和坐守监视技术人员的工资的价格水平都与长期租赁不同。
P xx云服务器公司司同意支付短期租赁的成本。
以下是一台云服务器一个坐守监视技术人员的短期租赁费用。
数据模型与决策R.C.Coleman案例管理报告

数据模型与决策R.C.Coleman案例管理报告数据模型与决策,Richard Coleman(R.C.Coleman)是一家中小型零售企业的老板,他希望通过数据分析和决策模型来提高企业运营效率和利润。
为了帮助他实现这个目标,我首先需要了解他的企业目标和问题所在,然后根据情况设计适合他的数据模型和决策模型。
首先,我会和R.C.Coleman交流,了解他的企业目标和问题所在。
他可能面临的问题可能包括:销售额下滑、顾客流失率增加、库存过剩或不足、供应链管理不佳等等。
了解这些问题会帮助我确定设计数据模型的方向和决策模型的需求。
在了解了R.C.Coleman的目标和问题之后,我会开始设计数据模型。
数据模型可以包括以下几个方面:1. 销售数据模型:设计一个模型来跟踪和分析销售数据,包括销售额、销售额增长率、销售渠道、产品销售排名等等。
通过分析销售数据,可以帮助R.C.Coleman了解产品销售情况,调整销售策略,提高销售额。
2. 顾客数据模型:设计一个模型来跟踪和分析顾客数据,包括顾客流失率、顾客购买频率、顾客喜好等等。
通过分析顾客数据,可以帮助R.C.Coleman了解顾客需求,提供更好的产品和服务,增加顾客忠诚度。
3. 库存数据模型:设计一个模型来跟踪和分析库存数据,包括库存水平、库存周转率、库存成本等等。
通过分析库存数据,可以帮助R.C.Coleman了解库存状况,及时调整采购和销售策略,避免库存过剩或不足。
4. 供应链数据模型:设计一个模型来跟踪和分析供应链数据,包括供应商质量、供应商交货准时率、采购成本等等。
通过分析供应链数据,可以帮助R.C.Coleman了解供应链状况,选择合适的供应商,降低采购成本,提高交货准时率。
在设计完数据模型之后,我会开始设计决策模型。
决策模型可以根据数据模型的分析结果来制定具体的决策方案,例如:1. 销售策略决策模型:根据销售数据模型的分析结果,制定合适的销售策略,包括产品定价、促销活动等等。
数据模型决策 mba 案例

数据模型决策 mba 案例
以下是一些涉及数据模型决策的MBA案例:
1. 北方化工厂月生产计划安排:该案例涉及到如何根据历史数据和市场趋势制定合理的月度生产计划,以最大化产能利用率,减少库存,提高经济效益。
这需要运用统计分析和预测模型来预测市场需求和生产成本,从而做出最优决策。
2. 石华建设监理公司监理工程师配置问题:该案例关注如何合理配置监理工程师,以确保工程项目进度和质量的同时,降低人力成本。
这需要运用数据分析模型来预测工程进度和人力需求,以便做出最佳的人员调度决策。
3. 北方印染公司应如何合理使用技术培训费:该案例探讨如何将有限的技术培训费用用于提高员工技能和素质,从而提高生产效率和产品质量。
这需要运用数据分析工具来分析员工技能需求和培训投资回报率,以便做出明智的投资决策。
4. 光明制造厂经营报告书:该案例涉及到如何通过财务数据和经营报告来评估企业的经营状况和未来发展趋势。
这需要运用财务分析模型和预测模型来评估企业的盈利能力、偿债能力和发展潜力,以便做出合理的战略规划和管理决策。
除了上述案例,MBA课程中还可能包含其他类似的案例,涉及不同行业的不同数据模型决策问题。
通过分析这些案例,学生可以了解实际商业环境中数据模型决策的重要性和应用价值,并学习如何运用数据分析工具和模型来解决复杂的商业问题。
数据驱动决策成功案例

数据驱动决策成功案例近年来,随着大数据技术的不断发展,数据在各行各业中扮演着越来越重要的角色。
数据驱动决策成为许多企业和组织追求的目标,因为通过数据分析和挖掘,可以为决策者提供准确、全面的信息,从而帮助他们做出明智的决策。
本文将通过几个成功案例来展示数据驱动决策的重要性和效果。
案例一:在线零售商的收益提升某在线零售商通过收集和分析顾客的购物行为数据,利用数据挖掘技术找到了顾客购买的关键影响因素,并根据这些因素制定了一系列针对性的营销策略。
他们根据顾客的历史购买记录和浏览行为,将其分为几个不同的目标群体,并向每个群体推送个性化的商品推荐和促销信息。
通过这样的方式,他们不仅提高了顾客的购买转化率,还增加了顾客的购买频次和客单价,从而实现了销售额的大幅度增长。
案例二:银行的风险管理一家大型银行通过对大量的历史交易数据进行分析,建立了一套完善的风险管理模型。
通过这个模型,银行能够对借款人的信用风险进行评估,并合理确定贷款利率和额度。
此外,银行还使用数据分析技术监测交易活动,及时发现异常行为和欺诈行为,以减少风险和损失。
这种数据驱动的风险管理体系不仅提高了银行的盈利能力,还改善了客户的体验和满意度。
案例三:药品销售预测一家制药公司通过分析销售数据和市场趋势,建立了一个药品销售预测模型。
通过这个模型,公司可以准确预测不同药品在不同时间和地点的需求,并相应地进行生产计划和库存管理。
这使得公司能够避免库存积压和药品过期等问题,并在销售高峰期满足市场需求,提高销售额和市场份额。
案例四:城市交通管理一些城市利用交通传感器和智能交通系统收集大量的交通数据,通过数据分析和模型建立,实现了优化交通流动和减少拥堵的目标。
他们根据数据分析的结果,调整红绿灯的时长,优化交通信号配时,提供实时交通信息和路线推荐等服务,以便驾驶员选择最优化的出行路径。
这些措施显著减少了交通拥堵,提高了通行效率,为城市居民提供了更好的交通体验。
以上是几个数据驱动决策成功案例的简要介绍。
《数据模型与决策》课件

04
实际案例分析
案例一:基于数据模型的营销决策
总结词
通过数据模型分析市场趋势,制定有效的营销策略。
详细描述
利用大数据和统计模型分析消费者行为和市场趋势,预 测未来市场需求,制定个性化的营销策略,提高销售业 绩和市场占有率。
总结词
优化营销预算分配。
详细描述
通过数据分析确定各营销渠道的投资回报率,合理分配 营销预算,提高营销效果和投资回报率。
03
未来还需要加强数据安全和隐 私保护等方面的研究,以保障 数据的安全性和可靠性。
数据模型与决策的实际应用价值
数据模型与决策在企业管理 中具有重要的应用价值,可 以帮助企业进行科学决策和
优化资源配置。
数据模型与决策还可以帮助 企业提高市场竞争力,如通 过数据分析发现市场趋势和 消费者需求,制定更加精准
总结词
提升客户满意度和忠诚度。
详细描述
通过数据模型分析客户反馈和行为数据,了解客户需求 和期望,优化产品和服务,提高客户满意度和忠诚度。
案例二:基于数据模型的金融风险评估
总结词
利用数据模型评估贷款违约风险。
01
02
详细描述
通过分析历史数据和信贷信息,利用统计模 型和机器学习算法评估贷款违约风险,为金 融机构提供风险预警和决策支持。
数据模型在决策中的作用
数据模型为决策提供数据支持
通过建立数据模型,将原始数据转化为有价值的信息,帮助决策者 更好地理解数据,从而做出更准确的决策。
数据模型提高决策效率
数据模型可以对大量数据进行处理和分析,快速得出结果,提高决 策效率。
数据模型降低决策风险
通过数据模型的预测和模拟功能,可以预测未来趋势,帮助决策者 提前做好准备,降低决策风险。
《数据模型与决策》案例分析报告-劳动力安排

基本思路
6
问题界定: 戴维斯仪器公司劳动力分配问题属于典型的线 性规划问题
解决方案 确定目标函数,采用线性模型求解
模型与使用工具 成本最小化模型 Excel中线性规划求解功能求解
分析过程
7
目标函数:
MinY=2000*Xi1+4800*Xi2+7500*Xi3+875(Xi1+Xi2+Xi3) Xi1:雇用一个月临时工数目 Xi2:雇用二个月临时工数目 Xi3:雇用三个月临时工数目 Y:总花费
0
0
10
0
23
0
19
0
26
20
14
0
112
分析过程
12
项目 费用 人数 合计 总费用
费用统计表 1个月工资/人 2个月工资/人 3个月工资/人
培训费 用
2000
4800
7500
700
112
0
0
112
224000
0
302400
0
78400
分析过程
13
总结:
1、总费用为$302400,比培训费用为$875/人, $减少11125
2000 7
费用统计表
2个月工资/ 3个月工资/
人
人
4800 3
7500 13
全职工 资
15840 10
培训费用 /人
875 33
合计
14000
14400
97500 158400 28875
总费用 313175
从计算结果可以看出,总费用会比全部雇用临时工少$350,因为培训 费用虽然可以减少$ 8750,但是工资却增加$ 8400,所以在培训费用 较高的情况下,多雇用全职员工可减少总费用;在培训费用较低的情 况下,就尽量少雇用全职员工。例如:当培训费用减少至$ 700时, 若雇用10名全职工,总费用将增加$ 5000。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:
(1)运用SPSS对价格进行频数分析,检验结果如下:
Statistics
P
N Valid 80
Missing 0
Mean 18.0774
Median 17.4100
Mode 14.00
Std. Deviation 8.06774
Skewness .677
Std. Error of Skewness .269
Kurtosis .382
Std. Error of Kurtosis .532
Minimum 4.90
Maximum 44.84
Percentiles 25 12.0000
50 17.4100
75 23.5700
观察结果可知,全部80中饼干价格在4.90-44.84之间波动,价格水平居中的40种饼干的价格在12到23.57之间波动,按此思路,其代表价格为17.41元。
(2)观察80种价格的平均值、中位数、众数,发现众数与平均值、中位数相差很远,故众数并不能代表全部80种饼干价格。
(3)使用平均数公式计算平均价格,知其结果为18.0774。
运用SPSS工具,可以画价格直方图如下:
观察直方图,我们发现价格可能服从正态,因此,我们对价格进行One-Sample KS Test,检验结果如下:
One-Sample Kolmogorov-Smirnov Test
P
N 80
Normal Parameters a Mean 18.08
Std. Deviation 8.068
Most Extreme Differences Absolute .101
Positive .101
Negative -.051
Kolmogorov-Smirnov Z .900
Asymp. Sig. (2-tailed) .393
a. Test distribution is Normal.
K-S检验的原假设为价格有服从正态分布的可能,备择假设为价格没有服从正态分布的可能,观察结果可知,检验P值为0.393,大于显著性水平0.05,故没有充分理由拒绝原假设,即不排除价格有服从正态分布的可能,由于正态分布对称,所以平均价格可以代表80种产品的价格。
(4)我们对80种饼干价格0-50之间,以组距为5分组,画直方图和频数多边形如下:
观察发现,价格主要分布在5-35之间,最多的一组数据在10-15之间,两端的值都比较少。
(5)用SPSS 作价位-销售状态的交叉分组,如下所示:
观察上述结果,我们发现价格越低,销售状态越好,价格越高,滞销的可能性越大,即两者呈现负相关,同时,处于中间水平的两种组合次低价-上中、次高价-下中也有很大的比重。
同时,观察列联表独立性检验的P值,为0.00,小于显著性水平0.05,故拒绝原假设,即价位和销售状态这两个变量不独立,这也验证了两者是存在相关性的。
(6)利用SPSS,我们做价格和销售量的散点图如下:
观察上图可发现价格和销售量有弱的负相关关系,即随着价格的增加,销售量呈下降趋势,我们进一步计算他们的相关系数,如下:
Correlations
Q P
Q Pearson Correlation 1 -.361**
Sig. (2-tailed) .001
N 80 80
P Pearson Correlation -.361** 1
Sig. (2-tailed) .001
N 80 80
**. Correlation is significant at the 0.01 level (2-tailed).
检验的P值为0.01,小于显著性水平0.05,说明两者的关系是显著地,同时,价格与销售量的相关系数为-0.361,说明两者成弱的负相关关系,即随着价格的上升,销售量呈下降趋势。
(7)第(6)步与前一步所得结果一致,结论都是价格与销售量之间呈现弱的负相关。
(8)需要知道购买者的收入水平,收入高的,自然对价格高的有更多的偏好,收入低的,对价格低的有偏好,故需要针对不同人群进行分析。
