初中数学中求极值的几种常见的方法
初中数学中求极值的几种常见的方法

初中数学中求最值的几种常见方法仪陇县实验学校 李洪泉在生活实践中,人们经常面对求最值的问题:如在一定方案中,往往会讨论什么情况下花费最低、消耗最少、产值最高、获利最大等;在解数学题时也常常求某个变量的最大值或最小值.同时,探求最值也是中考或一些高中学校自主招生考试中的一个热点内容,是初高中知识衔接的重要内容。
这类问题涉及变量多,综合性强,技巧性强,要求学生要有较强的数学转化思想和创新意识。
下面从不同的角度讨论如何求一些问题的最值。
一 、根据绝对值的几何意义求最值实数的绝对值具有非负性,0a ≥,即a 的最小值为0,但根据绝对值的代数意义求一些复杂问题的最值就要采用分类讨论法,比较麻烦.若根据绝对值的几何意义求最值就能够把一些复杂的问题简单化。
例1:已知13M x x =-++,则M 的最小值是 . 【思路点拨】用分类讨论法求出13x x -++的最小值是4,此时31x -≤≤。
如果我们从绝对值的几何意义来看此题,就是在数轴上求一点,使它到点1和点3-的距离之和为最短.显然,若3x <-,距离之和为[1(3)]2(3)4x --+-->;若31x -≤≤,距离之和为1(3)4--=;若1x >,距离之和为[1(3)]2(1)4x --+->。
所以, 当31x -≤≤时,距离之和最短,最小值为4。
故M 的最小值为4。
二、利用配方法求最值完全平方式具有非负性,即2()0a b +≥。
一个代数式若能配方成2()m a b k ++的形式,则这个代数式的最小值就为k 。
例2:设,a b 为实数,求222a ab b a b ++--的最小值。
【思路点拨】一是将原式直接配方成与,a b 的完全平方式有关的式子可以求出最小值。
二是引入参数设222a ab b a b t ++--=,将等式整理成关于a 的二次方程,运用配方法利用判别式求最值。
解:(方法一) 配方得:当10,10,2b a b -+=-=即0,1a b ==时,上式中不等号的等式成立,故所求的最小值为222222222(1)21331()242413()(1)1124a ab b a b a b a b b b a b b b a b ++--=+-+--=++---=++--≥-1-。
求极值的方法与技巧

求极值的方法与技巧
一、求函数极值的最基本方法
1、用微积分中的导数(Derivatives)法。
即要求函数极值问题,可
以将其转化为求解极值点,也就是求求函数的导函数为0时,函数的值最
大最小的解,即求函数的极值点。
2、用泰勒展开(Taylor Series)法。
这是一种利用因式分解法求函
数极值。
如果一个函数f(x)可以被表示为f(x),则它就可以按一定形式
分解成:f(x)=a₁+a₂x+a₃x2+a₄x3....,在这种分解的基础上,再算出
f'(x)=a₂+2a₃x+3a₄x2....,将f'(x)的值设置为0,即可求出此时函数f(x)的极值点。
3、用函数增减(Functional Increasing and Decreasing)法:研
究函数的单调增减性,通过对函数的单调增减性来判断函数的极大值和极
小值。
根据单调性原理,函数在单调递增的区间或单调递减的区间内,极值
只有一个,该函数极值即为极大值或极小值。
当函数在同一区间内的一些
点发生折点时,这个折点对应的函数值,即为函数在整个区间的极值,此
时的折点为函数的极值点。
二、极值点的确定方法
1、求解函数的单调性。
单调性主要是指函数在其中一区间上的曲线
轨迹是单调递增或者是单调递减的。
当函数在区间内的特定点发生折点时,这个折点就是函数的极值点。
2、求解导函数的。
初中数学最值问题六种模型

初中数学最值问题有六种模型,包括将军饮马模型、一箭穿心模型、费马点模型、阿氏圆模型、胡不归模型和瓜豆原理模型。
1. 将军饮马模型:当两定点A、B在直线l同侧时,在直线上找一点P,使PA+PB最小。
可以理解为两点之间线段最短。
连接AB交直线l于点P,点P即为所求作的点。
2. 一箭穿心模型:在直线l上找M、N两点(M在左),使得AM+MN+NB最小,且MN=d。
将点A向右平移d个单位到A′,作A′关于直线l的对称点A",连接A"B交直线l 于点N,将点N向左平移d个单位到M,点M、N即为所求。
3. 费马点模型:在三角形ABC中,若D、E分别是AB、AC 上的点,则DE的延长线与BC的延长线交于费马点处,此时三角形周长最小。
4. 阿氏圆模型:以给定点A为圆心,给定距离r为半径画圆,与已知直线l相交于两点B、C,连接两点B、C并延长交于D。
则D点的轨迹是以A为圆心,r为半径的圆。
这个圆被称为阿氏圆。
5. 胡不归模型:在直角三角形ABC中,AB=c,AC=b,BC=a,AD为BC边上的高。
若点P在BC边上,问是否存在点P使得DP垂直于BC边?如果存在,求出点P的位置;
如果不存在,请说明理由。
6. 瓜豆原理模型:在一条直线上有若干个点,每个点都有一个到直线的距离,问如何选择若干个点使得这些点到直线的距离之和最小?瓜豆原理告诉我们,选择任意两个相邻的点并连接它们与直线的交点,然后选择第三个点与前两个点的距离之和最小即可。
以上是初中数学最值问题的六种模型,希望对解决这类问题有所帮助。
初中最值问题的常用解法及模型

初中最值问题的常用解法及模型
一、初中最值问题的常用解法及模型
1、图形法
图形法是通过绘制图形来解决一些最值问题,常用在局部最值和极值的求解中。
通常可以利用函数图像上的特点来求解极值,如凸函数的图像是一个凹函数图像,而凹函数的图像是一个凸函数图像,拐点和极小值点的坐标位置有特殊的关系等,通过这些特点我们可以分析出对应的最大值和最小值的坐标位置。
例如:求函数y=2x^2-3x+1在区间[-2,2]上的最值
解:
令2x^2-3x+1=0,得x=-1,得函数在该x的点处取得极值。
因此,在[-2,2]上函数的最大值为y=-2,最小值为y=4.
2、求导法
求导法是通过求导求解最值问题的方法,常用于求函数的最大值或最小值。
通过对函数求导,找到函数的导数为0的极值点,从而判断函数在该点的极值情况。
例如:求函数y=-2x^2-4x+3的极值
解:令y'=0,得-2x^2-4x+3=0,解得x=1/2,此时函数y取得极值,即y=-2(1/2)^2-4(1/2)+3=-5/4。
3、比较法
比较法是通过比较函数值的大小,或者比较函数一次导数的正负来求解问题的方法。
该方法常用于求比较复杂的最值问题,如求分段
函数的最大值。
例如:求函数y=6x-x^2在[-1,2]上的最小值
解:由函数y在[-1,2]上的一次导数关系可知,当x=-1时,y'=5>0,x=2时,y'=-2<0,可知该函数在[-1,2]上的最小值取决于在x=-1和x=2处函数的值,故有y=-1时的最小值为y=-7。
求极值的三种方法
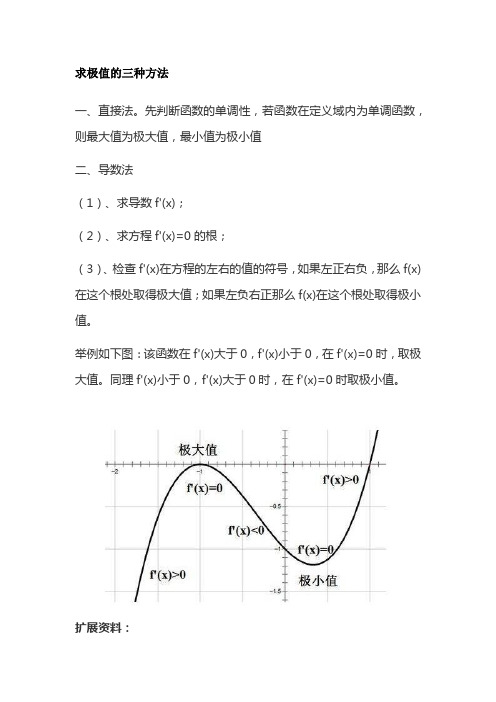
求极值的三种方法一、直接法。
先判断函数的单调性,若函数在定义域内为单调函数,则最大值为极大值,最小值为极小值二、导数法(1)、求导数f'(x);(2)、求方程f'(x)=0的根;(3)、检查f'(x)在方程的左右的值的符号,如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正那么f(x)在这个根处取得极小值。
举例如下图:该函数在f'(x)大于0,f'(x)小于0,在f'(x)=0时,取极大值。
同理f'(x)小于0,f'(x)大于0时,在f'(x)=0时取极小值。
扩展资料:寻求函数整个定义域上的最大值和最小值是数学优化的目标。
如果函数在闭合区间上是连续的,则通过极值定理存在整个定义域上的最大值和最小值。
此外,整个定义域上最大值(或最小值)必须是域内部的局部最大值(或最小值),或必须位于域的边界上。
因此,寻找整个定义域上最大值(或最小值)的方法是查看内部的所有局部最大值(或最小值),并且还查看边界上的点的最大值(或最小值),并且取最大值或最小的)一个。
1、求极大极小值步骤:求导数f'(x);求方程f'(x)=0的根;检查f'(x)在方程的左右的值的符号,如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正那么f(x)在这个根处取得极小值。
f'(x)无意义的点也要讨论。
即可先求出f'(x)=0的根和f'(x)无意义的点,再按定义去判别。
2、求极值点步骤:求出f'(x)=0,f"(x)≠0的x值;用极值的定义(半径无限小的邻域f(x)值比该点都小或都大的点为极值点),讨论f(x)的间断点。
上述所有点的集合即为极值点集合。
扩展资料:定义:若函数f(x)在x₀的一个邻域D有定义,且对D中除x₀的所有点,都有f(x)<f(x₀),则称f(x₀)是函数f(x)的一个极大值。
数学求极值

数学求极值在数学中,求极值是一个重要的概念和方法。
极值是函数在特定区间内取得的最大值或最小值。
通过求解极值,可以解决一系列实际问题,如优化问题、最大化利润、最小化成本等。
本文将介绍一些常见的数学求极值方法,并探讨其应用。
一、导数法导数法是求解极值的常用方法之一。
我们先来了解一下导数的概念。
在数学中,导数表示函数在某一点上的变化率。
对于函数f(x),它的导数可以用f'(x)或者dy/dx来表示。
对于一个函数f(x),如果在某一点x处的导数f'(x)等于0,那么这个点就是函数的极值点。
具体来说,如果f'(x)>0,那么函数在该点附近是递增的,这个点就是极小值点;如果f'(x)<0,那么函数在该点附近是递减的,这个点就是极大值点。
通过求导数,我们可以得到函数的极值点,进而确定函数的极值。
但是需要注意的是,并不是所有的导数为0的点都是极值点,还需要进一步判断。
例如,函数在某一点处的导数为0,但该点附近的导数都为正数,那么这个点就不是极值点。
二、二阶导数法在一些情况下,一阶导数法无法确定函数的极值点,这时候就需要使用二阶导数法。
二阶导数表示函数在某一点上的变化率的变化率。
具体来说,如果函数f(x)在某一点x处的二阶导数f''(x)>0,那么这个点就是函数的极小值点;如果f''(x)<0,那么这个点就是函数的极大值点。
通过求解二阶导数,我们可以进一步确定函数的极值。
但是需要注意的是,有时候二阶导数为0的点并不一定是极值点,还需要进一步判断。
例如,函数在某一点处的二阶导数为0,但该点附近的二阶导数都为负数,那么这个点就不是极值点。
三、拉格朗日乘数法拉格朗日乘数法是一种求解带有约束条件的极值问题的方法。
在一些实际问题中,我们往往需要在一定的约束条件下求解最优解。
比如,在一条直线上求解离该直线最近或最远的点,这就是一个带有约束条件的极值问题。
初中数学中求函数极值的常用解法举例

初中数学中求函数极值的常用解法举例罗江县函数极值是指函数的最大值或最小值,此类问题在初中数学中比较常见。
它涉及的知识面广,综合性强,有着极为丰富的内涵,解法也颇具有技巧性。
解答这类问题需要根据具体的特点,采取不同的方法。
现举例介绍这类问题的常用解法,供大家参考。
一、配方法:配方法是初中数学中解题常用的方法,它是将已知代数式(等式)通过配方,变形成若干个完全平方式的形式,结合完全平方的非负性质,解决问题。
例1 :若 x , y 为实数,求 A=5 x 2 + 5 y 2 − 8 xy + 2 x +2y +5 的最小值。
分析与解:A=(4x 2 − 8 xy + 4 y 2)+(x 2 + 2 x + 1)+( y 2+ 2 y + 1 )+ 3 = ( 2x − 2 y ) 2 + ( x + 1) 2 + ( y + 1) 2 +3显然,当 x = −1,y = − 1 时,A 有最小值3。
二、消元法:消元法是把代数式(等式)中的几个元素转化为以某一元素为主元的函数,再结合已知条件,经过运算,使问题简化,便于求解。
例2 :若 2x + y + z = 40,3x+ y -z = 30 ,且x 、y 、 z 均为非负数,求 A = 5x + 3 y + 2z 的极值。
分析与解:由 2x + y + z = 40及3x + y − z = 30,得 x=2z -10,y=60-5z,又由 x ≥0,y ≥0得2z -10 ≥ 0, 60-5z ≥ 0,解得 5≤z ≤12,把 x=2z -10,y=60-5z 代入 A=5x+3y+2z得A=−3z+130,显然 A 是关于 z 的一次函数,且 A 随 z 增大而减小,所以 当 z=5 时,A 的最大值为115,当 z=12时,A 的最小值为94。
三、数形结合法: 数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来,通过“以形助数”或“以数解形”即通过抽象思维与形象思维的结合,可以使复杂问题简单化,抽象问题具体化,从而起到优化解题途径的目的。
初中数学中的极值习题

初中数学中的极值习题极值是数学中重要的概念之一,涉及了一系列的计算和推理方法。
在初中数学中,极值习题是一个重要的考察内容,能够帮助学生提高解题能力和思维逻辑能力。
本文将为大家介绍几个常见的初中数学中的极值习题。
一、函数极值的判断对于给定的函数,判断其极值,首先需要计算函数的导数。
导数可以帮助我们找到函数的变化趋势,从而确定极值点。
常见的函数极值习题包括:1. 求函数f(x)=x^2在区间[-1,1]上的极值点。
解析:首先求出函数f(x)=x^2的导数f'(x)=2x,然后找到导数为0的点,即2x=0,解得x=0。
然后判断0是否在区间[-1,1]内,这是关键。
由于0属于[-1,1],所以0是函数f(x)=x^2在区间[-1,1]上的极值点。
此时,f(0)=0^2=0,所以极小值和极大值都是0。
2. 求函数f(x)=3x^4-4x^3在区间[-1,2]上的极值点。
解析:首先求出函数f(x)=3x^4-4x^3的导数f'(x)=12x^3-12x^2,然后找到导数为0的点,即12x^3-12x^2=0,整理得到x^3-x^2=0,解得x=0或x=1。
然后判断这两个点是否在区间[-1,2]内。
由于0和1都属于[-1,2],所以0和1是函数f(x)=3x^4-4x^3在区间[-1,2]上的极值点。
此时,计算f(0)和f(1)得到极大值和极小值。
二、应用题除了基础的函数极值习题之外,还有一些常见的应用题需要运用极值概念进行解答。
下面介绍两个典型的应用题:1. 目标最大化问题某地以修建高压输电线路为例。
已知该地的山地起伏较大,现需要从发电站出发,将输电线路引至用电点,要求总线路长度最短。
如何选择线路走向,使得总线路长度最短?解析:这是一个求线路最短距离的问题,可以应用极值的概念进行解答。
首先,将起点和终点固定,然后确定目标点,通过计算不同目标点与起终点的距离,找到长度最短的线路。
2. 几何图形内接问题已知固定周长的凸四边形,如何确定四边形是正方形时,其面积最大?解析:这是一个求最大面积的问题,可以应用极值的概念进行解答。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学中求最值的几种常见方法仪陇县实验学校李洪泉在生活实践中,人们经常面对求最值的问题:如在一定方案中,往往会讨论什么情况下花费最低、消耗最少、产值最高、获利最大等;在解数学题时也常常求某个变量的最大值或最小值。
同时,探求最值也是中考或一些高中学校自主招生考试中的一个热点内容,是初高中知识衔接的重要内容。
这类问题涉及变量多,综合性强,技巧性强,要求学生要有较强的数学转化思想和创新意识。
下面从不同的角度讨论如何求一些问题的最值。
一、根据绝对值的几何意义求最值实数的绝对值具有非负性,0a,即a 的最小值为0,但根据绝对值的代数意义求一些复杂问题的最值就要采用分类讨论法,比较麻烦。
若根据绝对值的几何意义求最值就能够把一些复杂的问题简单化。
例1:已知13Mxx,则M 的最小值是。
【思路点拨】用分类讨论法求出13xx的最小值是4,此时31x。
如果我们从绝对值的几何意义来看此题,就是在数轴上求一点,使它到点1和点3的距离之和为最短。
显然,若3x ,距离之和为[1(3)]2(3)4x ;若31x,距离之和为1(3)4;若1x,距离之和为[1(3)]2(1)4x 。
所以,当31x 时,距离之和最短,最小值为4。
故M 的最小值为4。
二、利用配方法求最值完全平方式具有非负性,即2()0ab 。
一个代数式若能配方成2()m a b k 的形式,则这个代数式的最小值就为k 。
例2:设,a b 为实数,求222aab ba b 的最小值。
【思路点拨】一是将原式直接配方成与,a b 的完全平方式有关的式子可以求出最小值。
二是引入参数设222a ab b a bt ,将等式整理成关于a 的二次方程,运用配方法利用判别式求最值。
解:(方法一) 配方得:当10,10,2b ab 即0,1a b时,上式中不等号的等式成立,故所求的最小值222222222(1)21331()242413()(1)1124aabba ba b a b bb a bbb ab为1。
(方法二)令222aab ba bt ,整理得22(1)(2)0ab a bb t ,由题可知此关于a 的二次方程有实数解,当1b时,上式中不等号的等式成立,故t 的最小值为1,即原式的最小值为1。
例3:若12123y z x ,则222xyz 的最小值为()A .3 B.5914C.92D. 6【思路点拨】引入参数设12123y z x k ,则222xy z就可用含k 的代数式表示,再通过配方求最小值。
解:令12123y z xk ,则1,21,32xk y k z k,当514k时,上式中不等号的等式成立。
故222xyz 的最小值为5914。
三、利用对称图形求最值根据两点之间线段最短可以求出两条线段之和的最小值。
若两条线段在某条直线的同侧时,可以利用轴对称的性质将在某条直线同侧的两条线段转化成在该直线异侧的两条线段,进而求出最值。
例4、如下图,已知边长为8cm 的正方形AB C D ,点E 在A B 上,且2A Ecm 。
在对角线B D 上求作一点P ,使APEP 最短,并求出它的最小值。
【思路点拨】此题是要在B D 上找一点P ,使AP EP 的和最小。
根据“两点之间线段最短”,只需把A P 和EP 转化到一条线段上,这就需要找到E 点关于BD 的对称点。
正方形是轴对称图形,对角线B D 所在的直线是它的对称轴,而点E 的对称点E 在正方形的22222(1)4(2)0364103314243(1)14bb b t b btt bbtb2222222(1)(21)(32)5595914()141414x y zkk k k边B C 上,连结AE 交B D 于点P ,连结P E ,所以PE PE,AEAP E P APEP ,则点P 就是所求作的点。
要想求AP EP 的最小值,只要求AE的长即可。
与该图形类似的还有菱形、圆。
解:如上图,作出点E 关于B D 的对称点E ,在连接AE 交B D 于点P ,则点P 就是所求作的点。
由图可知228610APPEAE,即AP EP 的最小值为10。
例5、如下图,在平面直角坐标系中,已知点(2,4)A ,点(6,3)B ,分别在x 轴、y 轴上求作点,C D ,使四边形A BC D 的周长最短?并求出周长的最小值。
【思路点拨】已知点,A B 为定点,所以A B 的长固定不变,这样只要求出ADD CC B 的最小值即可。
要想求出它的最小值,设法把这三条线段构造在一条线段上,分别作出点,A B 的对称点,A B ,连接A B,与x 轴和y 轴分别交于点,C D ,则A BA DD C C B A D D C C B ,于是点,C D 就是所求作的点。
然后分别以,A B A B 为斜边构造R tA B E 和Rt A B F ,易知点E 坐标为(6,4),点F 坐标为(2,3),4,1AEBE,所以2217ABAE BE,同理可得,113A B ,则四边形A B C D 的周长的最小值是17+113。
四、根据垂线段最短求最值例6、(2011年南充中考)如图,等腰梯形A BC D 中,//,2,60,AD BC AD AB CD C M是B C 的中点。
(1)求证:M D C 是等边三角形;(2)将MDC绕点M 旋转,当M D (即M D )与A B 交于一点E ,M C (即M C )同时与AD 交于一点F 时,点,E F 和点A 构成AEF .试探究AEF的周长是否存在最小值。
如果不存在,请说明理由;如果存在,请计算出AEF 周长的最小值。
【思路点拨】易证B M EA M F .由此可推出2,AEAF AB同时可推出M E F 为等边三角形,进而得到EF M F ,根据“垂线段最短”可得M F 的最小值为点M到A D 的距离3,即E F 的最小值是3。
由此可得到AEF周长的最小值为23。
解:(1)略(2)AEF 的周长存在最小值.理由如下:连接A M ,由(1)可得ABM D 是菱形,,,MAB MAD MC D 是等边三角形,60BM ABM EAM E,60EM FAM FAM EBM EAM F在B M E 与AM F 中,,60BM AM EBMFAM()BMEAMF ASA ,,BE AF ME MF AEAFAEBEAB 60EM F D M C,故EM F 是等边三角形,EFM F∵M F 的最小值为点M 到A D 的距离3,即E F 的最小值是3。
A E F 的周长AEAFEFABEFA E F 的周长的最小值为2+3.五、利用一次函数与二次函数的性质求最值一次函数ykxb 的图像是一条直线。
当自变量x 取一切实数时,函数y 不存在最值。
但当自变量x 定义在某一区间内时,x 存在着最值,函数y 也就存在着最值。
二次函数2y axbxc 的图像是一条抛物线。
当自变量x 取一切实数时,抛物线顶点的纵坐标就是函数y 的最值。
当自变量x 定义在某一区间的条件限制时,函数y 的最值有以下两种情况:(1)当抛物线的顶点在该区间内时,顶点的纵坐标就是函数y 的最值。
(2)当抛物线的顶点不在该区间内时,函数y 的最值在区间内两端点处取得。
例7:某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按120个工时计算)生产空调器、彩电、冰箱共360台,且冰箱至少生产60台,已知生产这些家电产品每台所需工时和每台产值如下表家电名称空调彩电冰箱工时213141产值(千元)432问每周应生产空调器、彩电、冰箱各多少台,才能使产值最高?最高产值是多少(以千元为单位)?【思路点拨】根据题意,可分别令生产空调器x 台,彩电y 台,冰箱z 台,总产值(M 千元),易得总产值(M 千元)与冰箱z 台成一次函数关系。
60z,M 存在最值。
解:分别令生产空调器x 台,彩电y 台,冰箱z 台,总产值为(M 千元),由题可得:36011112023443260x y z x yzM x yz z 整理得:11080(60)2Mz z,因为10,2kM 随z增大而减小,所以当60z 时,M 有最大值,即M 的最大值为160108010502(千元). 当60z时,720330,27022z zxy.故:每周应生产空调器30台,彩电270台,冰箱60台,才能使产值最高,最高产值为1050千元。
例8:设12,x x 是方程22242320xmx mm 的两个实根,当m 为何值时,2212x x 有最小值,并求这个最小值。
【思路点拨】由韦达定理可知2212x x 是关于m 的二次函数,从判别式入手,根据m 的取值范围可分析出2212x x 的最小值。
解:由题可知22(4)42(232)0m m m ,解得:23m.令2212yx x ,则22212124232()2()222m mm yx x x x 2232mm 即22232()3ym m m .由函数图像可知,当23m 时,y 有最小值,最小值为22282()32339.故:当23m时,2212x x 有最小值,最小值为89.例9:(2011年南充中考)某工厂在生产过程中要消耗大量电能,消耗每千度电产生利润与电价是一次函数关系,经过测算,工厂每千度电产生利润y(元/千度))与电价x(元/千度)的函数图象如图:(1)当电价为600元/千度时,工厂消耗每千度电产生利润是多少?(2)为了实现节能减排目标,有关部门规定,该厂电价x(元/千度)与每天用电量m(千度)的函数关系为x=10m+500,且该工厂每天用电量不超过60千度,为了获得最大利润,工厂每天应安排使用多少千度电?工厂每天消耗电产生利润最大是多少元?【思路点拨】根据图像易求出每千度电产生利润y (元/千度)与电价x (元/千度)的函数解析式为1300(0)5yxx。
令工厂每天消耗电产生利润为W 元,易得211(300)(10500)3002200(060)55W m y m x mm mm m,根据二次函数的性质即可求出W 的最大值。
解:(1)略(2)设工厂每天消耗电产生利润为W 元,由题意得:211(300)(10500)3002200(060)55Wm ym xmm mm m 化简配方,得:22(50)5000(060)W mm ∴当50m时,=5000W 最大。
即当工厂每天消耗50千度电时,工厂每天消耗电产生利润最大为5000元.六、利用均值定理求最值当,a b 均为正实数,且abk (定值)时,2abab (定值)当且仅当ab时取等号,此定理称为均值定理。
运用均值定理求最值要同时满足“一正、二定、三相等”三个条件。
多数运用均值定理求最值的问题的条件具有隐蔽性,需要适当地变形才能用均值定理求解。
