初中数学极值问题

合集下载

初中数学中求极值的几种常见的方法

初中数学中求最值的几种常见方法仪陇县实验学校李洪泉在生活实践中,人们经常面对求最值的问题：如在一定方案中，往往会讨论什么情况下花费最低、消耗最少、产值最高、获利最大等；在解数学题时也常常求某个变量的最大值或最小值.同时,探求最值也是中考或一些高中学校自主招生考试中的一个热点内容,是初高中知识衔接的重要内容。

这类问题涉及变量多，综合性强,技巧性强，要求学生要有较强的数学转化思想和创新意识。

下面从不同的角度讨论如何求一些问题的最值。

一、根据绝对值的几何意义求最值实数的绝对值具有非负性,0a ≥，即a 的最小值为0，但根据绝对值的代数意义求一些复杂问题的最值就要采用分类讨论法，比较麻烦.若根据绝对值的几何意义求最值就能够把一些复杂的问题简单化。

例1:已知13M x x =-++，则M 的最小值是 . 【思路点拨】用分类讨论法求出13x x -++的最小值是4，此时31x -≤≤。

如果我们从绝对值的几何意义来看此题，就是在数轴上求一点，使它到点1和点3-的距离之和为最短.显然,若3x <-,距离之和为[1(3)]2(3)4x --+-->；若31x -≤≤,距离之和为1(3)4--=；若1x >,距离之和为[1(3)]2(1)4x --+->。

所以，当31x -≤≤时,距离之和最短,最小值为4。

故M 的最小值为4。

二、利用配方法求最值完全平方式具有非负性，即2()0a b +≥。

一个代数式若能配方成2()m a b k ++的形式，则这个代数式的最小值就为k 。

例2:设,a b 为实数，求222a ab b a b ++--的最小值。

【思路点拨】一是将原式直接配方成与,a b 的完全平方式有关的式子可以求出最小值。

二是引入参数设222a ab b a b t ++--=，将等式整理成关于a 的二次方程，运用配方法利用判别式求最值。

解：（方法一) 配方得：当10,10,2b a b -+=-=即0,1a b ==时,上式中不等号的等式成立,故所求的最小值为222222222(1)21331()242413()(1)1124a ab b a b a b a b b b a b b b a b ++--=+-+--=++---=++--≥-1-。

初中数学100道最值问题经典

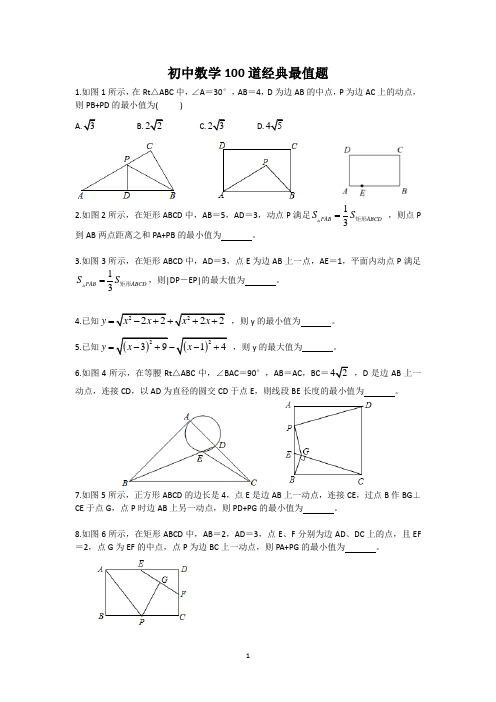
初中数学100道经典最值题1.如图1所示，在Rt △ABC 中，∠A ＝30°，AB ＝4，D 为边AB 的中点，P 为边AC 上的动点，则PB+PD 的最小值为( )B. C. D.2.如图2所示，在矩形ABCD 中，AB ＝5，AD ＝3，动点P 满足13PAB ABCD S S =矩形，则点P 到AB 两点距离之和PA+PB 的最小值为。

3.如图3所示，在矩形ABCD 中，AD ＝3，点E 为边AB 上一点，AE ＝1，平面内动点P 满足13PAB ABCD SS =矩形，则|DP －EP|的最大值为。

4.已知y ，则y 的最小值为。

5.已知y =，则y 的最大值为。

6.如图4所示，在等腰Rt △ABC 中，∠BAC ＝90°，AB ＝AC ，BC ＝，D 是边AB 上一动点，连接CD ，以AD 为直径的圆交CD 于点E ，则线段BE 长度的最小值为。

7.如图5所示，正方形ABCD 的边长是4，点E 是边AB 上一动点，连接CE ，过点B 作BG ⊥CE 于点G ，点P 时边AB 上另一动点，则PD+PG 的最小值为。

8.如图6所示，在矩形ABCD 中，AB ＝2，AD ＝3，点E 、F 分别为边AD 、DC 上的点，且EF ＝2，点G 为EF 的中点，点P 为边BC 上一动点，则PA+PG 的最小值为。

9.在平面直角坐标系中，A(3，0)，B(a，2)，C(0，m)，D(n，0)，且m2+n2＝4，若点E为CD 的中点，则AB+BE的最小值为。

A.3B.4C.5D.2510.如图7所示，AB＝3，AC＝2，以BC为边向上构造等边三角形BCD，则AD的取值范围为。

11.如图8所示，AB＝3，AC＝2，以BC为腰(点B为直角顶点)向上构造等腰直角三角形BCD，则AD的取值范围为。

12.如图9所示，AB＝4，AC＝2，以BC为底边向上构造等腰直角三角形BCD，则AD的取值范围为。

初中数学,隐圆与极值问题经典题型.doc

初中数学，隐圆与极值问题经典题型有关隐圆比较经典的极值题型总结，分享如下：1、矩形ABCD，M为边AB上一动点，沿着DM翻折△MDA得到△MDA1，则BA1的最小值是2、如图，E，F是正方形ABCD的边AD上两个动点，满足AE=DF．连接CF交BD于点G，连接BE交AG于点H．若正方形的边长为2，则线段DH长度的最小值是3、如图，边长为3的等边△ABC，D、E分别为边BC、AC上的点，且BD＝CE，AD、BE交于P点，则CP的最小值为4、如图，Rt△ABC中，AB⊥BC，AB=2，BC=3，P是△ABC 内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值为．5、如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，D 为AB边上一点，过点D作CD的垂线交直线BC于点E，则线段CE长度的最小值是6、Rt△ABC中, ∠C＝90°, ∠ABC＝30°,AB＝6, D在AB 边上, 点E是BC边上一点(不与点B、C重合), 且DA＝DE,则AD的最小值是7、如图，∠xOy=45°，把线段的两个顶点A,B分别在Ox，Oy上移动，其中AB=10，点O到AB的距离的最大值为8、如图4，在边长为2的菱形ABCD中，∠A=60°，M 是AD边的中点，N是AB边上一动点，将△AMN沿直线MN翻折得到△A1MN,连接CA1,BA1.（1）A1B长度的最小值是（2）A1C长度的最小值是9、四边形ABCD中，AD∥BC，∠A=90,AD=1，AB=2,BC=3,P是线段AD上一动点，将△ABP沿BP所在直线翻折得到△QBP，则△CQD的面积最小值为10、如图，半圆O的半径为1，AC⊥AB，BD⊥AB，且AC=1，BD=3，P是半圆上任意一点，则封闭图形ABDPC 面积的最大值是11、如图，P为圆O内一个定点，A为圆O上一个动点，射线AP,AO分别与圆O交于B，C两点，若圆O的半径为3，OP=，则弦BC的最大值为________12、已知A（2，0），B（5，0），点P为圆A上一动点，圆A半径为2，以PB为边作等边△PMB，求线段AM的取值范围。

中学生求极值的方法

中学生求极值的方法
在研究中，求极值是一个重要的部分，其中的基本概念是找出函数的最大值或最小值。

研究如何求极值有助于中学生们更好地理解函数的性质以及在实际工作中的应用。

因此，本文将讨论求极值的方法，以帮助中学生更好地研究和理解。

首先，让我们来了解求极值的基本概念。

求极值，也称为极值问题，是指在给定条件下，求出函数f (x)的最大值或最小值的问题。

这就是求极值的基本概念，在实际应用中，也被称为极值优化问题。

其次，让我们来了解求极值的方法。

在实际应用中，求极值的方法主要有以下几种：
1、图像法：通过绘制函数的图像，找出函数的极值点，从而求出极值的值。

2、微分法：通过对函数求导，求出函数的一阶导数为0时，函数的极值点，从而求出极值的值。

3、数值法：通过给出函数的可行域，将可行域离散为若干区间，然后在每个区间精确求出函数的最大值和最小值，从而求出极值的值。

最后，我们来看看如何将这些方法应用到实际中。

1、先确定函数的可行域，从而确定求极值的范围；
2、根据函数的性质，选择适当的求极值方法，进行求极
值操作；
3、根据求极值的结果，得出函数的最大值或最小值。

通过以上内容，我们可以看出，求极值是一个重要的部分，中学生应该掌握求极值的基本概念和方法，以帮助他们更好地理解函数的性质和在实际工作中的应用。

初中数学最值问题六种模型

初中数学最值问题有六种模型，包括将军饮马模型、一箭穿心模型、费马点模型、阿氏圆模型、胡不归模型和瓜豆原理模型。

1. 将军饮马模型：当两定点A、B在直线l同侧时，在直线上找一点P，使PA+PB最小。

可以理解为两点之间线段最短。

连接AB交直线l于点P，点P即为所求作的点。

2. 一箭穿心模型：在直线l上找M、N两点（M在左），使得AM+MN+NB最小，且MN=d。

将点A向右平移d个单位到A′，作A′关于直线l的对称点A"，连接A"B交直线l 于点N，将点N向左平移d个单位到M，点M、N即为所求。

3. 费马点模型：在三角形ABC中，若D、E分别是AB、AC 上的点，则DE的延长线与BC的延长线交于费马点处，此时三角形周长最小。

4. 阿氏圆模型：以给定点A为圆心，给定距离r为半径画圆，与已知直线l相交于两点B、C，连接两点B、C并延长交于D。

则D点的轨迹是以A为圆心，r为半径的圆。

这个圆被称为阿氏圆。

5. 胡不归模型：在直角三角形ABC中，AB=c，AC=b，BC=a，AD为BC边上的高。

若点P在BC边上，问是否存在点P使得DP垂直于BC边？如果存在，求出点P的位置；
如果不存在，请说明理由。

6. 瓜豆原理模型：在一条直线上有若干个点，每个点都有一个到直线的距离，问如何选择若干个点使得这些点到直线的距离之和最小？瓜豆原理告诉我们，选择任意两个相邻的点并连接它们与直线的交点，然后选择第三个点与前两个点的距离之和最小即可。

以上是初中数学最值问题的六种模型，希望对解决这类问题有所帮助。

初中最值问题的常用解法及模型

初中最值问题的常用解法及模型
一、初中最值问题的常用解法及模型
1、图形法
图形法是通过绘制图形来解决一些最值问题，常用在局部最值和极值的求解中。

通常可以利用函数图像上的特点来求解极值，如凸函数的图像是一个凹函数图像，而凹函数的图像是一个凸函数图像，拐点和极小值点的坐标位置有特殊的关系等，通过这些特点我们可以分析出对应的最大值和最小值的坐标位置。

例如：求函数y=2x^2-3x+1在区间[-2,2]上的最值
解：
令2x^2-3x+1=0，得x=-1，得函数在该x的点处取得极值。

因此，在[-2,2]上函数的最大值为y=-2，最小值为y=4.
2、求导法
求导法是通过求导求解最值问题的方法，常用于求函数的最大值或最小值。

通过对函数求导，找到函数的导数为0的极值点，从而判断函数在该点的极值情况。

例如：求函数y=-2x^2-4x+3的极值
解：令y'=0，得-2x^2-4x+3=0，解得x=1/2，此时函数y取得极值，即y=-2(1/2)^2-4(1/2)+3=-5/4。

3、比较法
比较法是通过比较函数值的大小，或者比较函数一次导数的正负来求解问题的方法。

该方法常用于求比较复杂的最值问题，如求分段
函数的最大值。

例如：求函数y=6x-x^2在[-1,2]上的最小值
解：由函数y在[-1,2]上的一次导数关系可知，当x=-1时，y'=5>0，x=2时，y'=-2<0，可知该函数在[-1,2]上的最小值取决于在x=-1和x=2处函数的值，故有y=-1时的最小值为y=-7。

中学数学利用导数研究函数的极值和最值(含答案)

专题4 利用导数研究函数的极值和最值专题知识梳理1.函数的极值（1）函数极值定义:一般地，设函数在点附近有定义，如果对附近的所有的点，都有，就说是函数的一个极大值，记作y极大值=,是极大值点。

如果对附近的所有的点，都有.就说是函数的一个极小值，记作y 极小值=，是极小值点。

极大值与极小值统称为极值.(2)判别f (x 0)是极大、极小值的方法:若满足，且在的两侧的导数异号，则是的极值点，是极值，并且如果在两侧满足“左正右负”，则是的极大值点，是极大值；如果在两侧满足“左负右正”，则是的极小值点，是极小值. (3)求可导函数f (x )的极值的步骤: ①确定函数的定义区间，求导数 ; ①求出方程的定义域内的所有实数根；①用函数的导数为的点，顺次将函数的定义域分成若干小开区间，并列成表格.标出在方程根左右的值的符号，如果左正右负，那么f (x )在这个根处取得极大值；如果左负右正，那么f (x )在这个根处取得极小值；如果左右不改变符号，那么f (x )在这个根处无极值。

①根据表格下结论并求出需要的极值。

2. 函数的最值（1）定义：若在函数的定义域内存在,使得对于任意的,都有,则称为函数的最大值，记作;若在函数的定义域内存在,使得对于任意的,都有,则称为函数的最小值，记作;（2）在闭区间上图像连续不断的函数在上必有最大值与最小值．（3）求函数在上的最大值与最小值的步骤： ①求在内的极值；①将的各极值与比较，其中最大的一个是最大值，最小的一个是最小值, 从而得出函数在上的最值。

考点探究)(x f x 0x 0f (x )<f (x 0)f (x 0))(x f f (x 0)x 0x 0f (x )>f (x 0)f (x 0))(x f f (x 0)x 00x 0)(0='x f 0x )(x f 0x )(x f )(0x f )(x f '0x 0x )(x f )(0x f )(x f '0x 0x )(x f )(0x f )(x f '¢f (x )=00)(x f ')(x f I x 0x ÎI f (x )£f (x 0))(0x f y max =f (x 0))(x f I x 0x ÎI f (x )³f (x 0))(0x f y min =f (x 0)[]b a ,)(x f []b a ,)(x f []b a ,)(x f (,)a b )(x f f (a ),f (b ))(x f []b a ,考向1 利用导数研究函数的极值【例】已知函数x xx f ln 1)(+=，求函数()f x 的极值. 【解析】因为1()ln f x x x =+，所以2111'()x f x x x x-=-+=,令，得x =1，列表:所以是f x 的极小值1，无极大值。

初中数学常见8种最值问题

的方程 3 B.初中数学常见8种最值问题最值问题，也就是最大值和最小值问题.它是初中数学竞赛中的常见问题. 这类问题出现的试题，内容丰富，知识点多，涉及面广，解法灵活多样，而且具有一定的难度.本文以例介绍一些常见的求解方法，供读者参考.一. 配方法例 1. （2005 年全国初中数学联赛武汉 CASIO 杯选拔赛）可取得的最小值为.解：原式由此可知，当时，有最小值 .二. 设参数法例 2. （《中等数学》奥林匹克训练题）已知实数满足 .则的最大值为.解：设，易知,由，得从而，.由此可知，是关于 t 的两个实根.于是，有,解得.故的最大值为 2.例 3. （2004 年全国初中联赛武汉选拔赛）若，则可取得的最小值为（）A. C.D. 6取得最小值 .故选（B ）.解：设，则从而可知，当时，解：由得解得由是非负实数，得 , 解得又，故，三. 选主元法例 4. （2004 年全国初中数学竞赛）实数满足.则 z 的最大值是.解：由得.代入消去 y 并整理成以为主元的二次方程，由 x 为实数，则判别式 . 即，整理得解得 .所以，z 的最大值是 .四. 夹逼法例 5. （2003 年北京市初二数学竞赛复赛）是非负实数，并且满足.设，记为 m 的最小值，y 为 m 的最大值.则.五. 构造方程法例 6. （2000 年山东省初中数学竞赛）.于是，因此.已知矩形 A 的边长为 a 和 b ，如果总有另一矩形 B 使得矩形 B 与矩形 A 的周长之比与面积之比都等于 k ，试求 k 的最小值.解：设矩形 B 的边长为 x 和 y ，由题设可得 .从而x 和y 可以看作是关于t 的一元二次方程的两个实数根，则 ,因为，所以，解得,所以 k 的最小值是.六. 由某字母所取的最值确定代数式的最值例 7. （2006 年全国初中数学竞赛）已知为整数，且.若，则的最大值为.解：由得，代入得.而由和可知的整数.所以，当时，取得最大值，为.七. 借助几何图形法例 8. （2004 年四川省初中数学联赛）函数的最小值是.解：显然，若，则.因而，当取最小值时，必然有. 如图1，作线段AB=4，，且AC=1，BD=2.对于AB 上的任一点O，令OA=x，则.那么，问题转化为在 AB 上求一点 O，使 OC+OD 最小.图 1设点 C 关于 AB 的对称点为 E，则 DE 与 AB 的交点即为点 O，此时，.作 EF//AB 与DB 的延长线交于 F.在中，易知，所以，.因此，函数的最小值为5.八. 比较法例 9. （2002 年全国初中数学竞赛）某项工程，如果有甲、乙两队承包天完成，需付180000 元；由乙、丙两队承包天完成，需付150000 元；由甲、丙两队承包天完成，需付160000 元. 现在工程由一个队单独承包，在保证一周完成的前提下，哪个队承包费用最少？解：设甲、乙、丙单独承包各需天完成，则解得又设甲、乙、丙单独工作一天，各需付元，则解得于是，由甲队单独承包，费用是（元）；由乙队单独承包，费用是（元）；而丙队不能在一周内完成，经过比较得知，乙队承包费用最少.。

初中数学中求函数极值的常用解法举例

初中数学中求函数极值的常用解法举例罗江县函数极值是指函数的最大值或最小值，此类问题在初中数学中比较常见。

它涉及的知识面广，综合性强，有着极为丰富的内涵，解法也颇具有技巧性。

解答这类问题需要根据具体的特点，采取不同的方法。

现举例介绍这类问题的常用解法，供大家参考。

一、配方法：配方法是初中数学中解题常用的方法，它是将已知代数式（等式）通过配方，变形成若干个完全平方式的形式，结合完全平方的非负性质，解决问题。

例1 ：若 x , y 为实数，求 A=5 x 2 + 5 y 2 − 8 xy + 2 x +2y +5 的最小值。

分析与解：A=（4x 2 − 8 xy + 4 y 2）+（x 2 + 2 x + 1）+（ y 2+ 2 y + 1 ）+ 3 = ( 2x − 2 y ) 2 + ( x + 1) 2 + ( y + 1) 2 +3显然，当 x = −1，y = − 1 时，A 有最小值3。

二、消元法：消元法是把代数式（等式）中的几个元素转化为以某一元素为主元的函数，再结合已知条件，经过运算，使问题简化，便于求解。

例2 ：若 2x + y + z = 40，3x+ y －z = 30 ，且x 、y 、 z 均为非负数，求 A = 5x + 3 y + 2z 的极值。

分析与解：由 2x + y + z = 40及3x + y − z = 30，得 x=2z －10，y=60－5z,又由 x ≥0，y ≥0得2z －10 ≥ 0， 60－5z ≥ 0,解得 5≤z ≤12，把 x=2z －10，y=60－5z 代入 A=5x+3y+2z得A=−3z+130，显然 A 是关于 z 的一次函数，且 A 随 z 增大而减小，所以当 z=5 时，A 的最大值为115，当 z=12时，A 的最小值为94。

三、数形结合法: 数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来，通过“以形助数”或“以数解形”即通过抽象思维与形象思维的结合，可以使复杂问题简单化，抽象问题具体化，从而起到优化解题途径的目的。

初中数学中的极值习题

初中数学中的极值习题极值是数学中重要的概念之一，涉及了一系列的计算和推理方法。

在初中数学中，极值习题是一个重要的考察内容，能够帮助学生提高解题能力和思维逻辑能力。

本文将为大家介绍几个常见的初中数学中的极值习题。

一、函数极值的判断对于给定的函数，判断其极值，首先需要计算函数的导数。

导数可以帮助我们找到函数的变化趋势，从而确定极值点。

常见的函数极值习题包括：1. 求函数f(x)=x^2在区间[-1,1]上的极值点。

解析：首先求出函数f(x)=x^2的导数f'(x)=2x，然后找到导数为0的点，即2x=0，解得x=0。

然后判断0是否在区间[-1,1]内，这是关键。

由于0属于[-1,1]，所以0是函数f(x)=x^2在区间[-1,1]上的极值点。

此时，f(0)=0^2=0，所以极小值和极大值都是0。

2. 求函数f(x)=3x^4-4x^3在区间[-1,2]上的极值点。

解析：首先求出函数f(x)=3x^4-4x^3的导数f'(x)=12x^3-12x^2，然后找到导数为0的点，即12x^3-12x^2=0，整理得到x^3-x^2=0，解得x=0或x=1。

然后判断这两个点是否在区间[-1,2]内。

由于0和1都属于[-1,2]，所以0和1是函数f(x)=3x^4-4x^3在区间[-1,2]上的极值点。

此时，计算f(0)和f(1)得到极大值和极小值。

二、应用题除了基础的函数极值习题之外，还有一些常见的应用题需要运用极值概念进行解答。

下面介绍两个典型的应用题：1. 目标最大化问题某地以修建高压输电线路为例。

已知该地的山地起伏较大，现需要从发电站出发，将输电线路引至用电点，要求总线路长度最短。

如何选择线路走向，使得总线路长度最短？解析：这是一个求线路最短距离的问题，可以应用极值的概念进行解答。

首先，将起点和终点固定，然后确定目标点，通过计算不同目标点与起终点的距离，找到长度最短的线路。

2. 几何图形内接问题已知固定周长的凸四边形，如何确定四边形是正方形时，其面积最大？解析：这是一个求最大面积的问题，可以应用极值的概念进行解答。

初三数学中考专题极值问题

极值问题1.实数x 、y 满足5422=--y x x 求x-2y 的取值范围。

2. 阅读理解：对于任意正实数a 、b ，∵2≥0，∴a b -≥0，∴a b +≥a ＝b 时，等号成立．结论：在a b +≥a 、b 均为正实数）中，若ab 为定值p ，则a+b≥a ＝b 时，a+b 有最小值根据上述内容，回答下列问题： (1)若m ＞0，只有当m ＝时，1m m+有最小值． (2)思考验证：如图，AB 为半圆O 的直径，C 为半圆上任意一点（与点A 、B 不重合），过点C 作CD ⊥AB ，垂足为D ，AD ＝a ，DB ＝b ．试根据图形验证a b +≥(3)探索应用：如图，已知A(－3，0)，B(0，－4)，P 为双曲线xy 12=（x ＞0）上的任意一点，过点P 作PC ⊥x 轴于点C ，PD ⊥y 轴于点D ．求四边形ABCD 面积的最小值，并说明此时四边形ABCD 的形状．3.已知点A 的坐标为（-4,8），点B 的坐标为（2，2）,⑴请在y 轴上找到一点P ，使PA+PB 最小，求出最小值、此时P 点的坐标。

⑵请在x 轴上找到一点P ，使PA+PB 最小，求出最小值、点P 的坐标； ⑶请在y 轴上找到一点P ，使PB PA -最大，求出最小值、P 点的坐标。

⑷在y 轴上找一点M ，使点M 到点C （-2，0）的距离和到直线AB 的距离之和最小，请求出最小值; 延伸若点'C 的坐标为（2，0），在y 轴上找一点N ，使点N 到点'C 的距离和到直线AB 的距离之和最小，请求出最小值(2)图(3)图⑸已知点A 的坐标为（-4,8），点B 的坐标为（2，2）,点C 的坐标为（-2，0），把点A 和点B 向左平移m 个单位，得到点'A 和点'B ,使'A C+C 'B 最短，求m 的值。

（6）如图，已知点A 的坐标为（-4,8），点B 的坐标为（2，2）,点C 的坐标为（-2，0），点D 的坐标为（-4，0），把点A 和点B 向左或向右平移m 个单位，得到点'A 和点'B ,使四边形'A 'B CD 的周长最短，求m 的值。

初中数学最值问题专题

初中数学最值问题专题中考数学最值问题【例题1】(经典题)⼆次函数y=2(x ﹣3)2﹣4得最⼩值为 .【例题2】(2018江西)如图,AB 就是⊙O 得弦,AB=5,点C 就是⊙O 上得⼀个动点,且∠ACB=45°,若点M 、N 分别就是AB 、AC 得中点,则MN 长得最⼤值就是 .【例题3】(2019湖南张家界)已知抛物线y ＝ax 2＋bx ＋c (a ≠0)过点A (1,0),B (3,0)两点,与y 轴交于点C ,OC ＝3. (1)求抛物线得解析式及顶点D 得坐标;(2)过点A 作AM ⊥BC ,垂⾜为M ,求证:四边形ADBM 为正⽅形;(3)点P 为抛物线在直线BC 下⽅图形上得⼀动点,当△PBC ⾯积最⼤时,求P 点坐标及最⼤⾯积得值; (4)若点Q 为线段OC 上得⼀动点,问AQ ＋QC 就是否存在最⼩值?若存在,求岀这个最⼩值;若不存在,请说明理由.练习1、(2018河南)要使代数式有意义,则x 得( )A 、最⼤值为B 、最⼩值为C 、最⼤值为D 、最⼤值为2、(2018四川绵阳)不等边三⾓形?ABC 得两边上得⾼分别为4与12且第三边上得⾼为整数,那么此⾼得最⼤值可能为________。

3、(2018齐齐哈尔)设a 、b 为实数,那么a ab b a b 222++--得最⼩值为_______。

4、(2018云南)如图,MN 就是⊙O 得直径,MN=4,∠AMN=40°,点B 为弧AN 得中点,点P 就是直径MN 上得⼀个动点,则PA+PB 得最⼩值为 .5、(2018海南)某⽔果店在两周内,将标价为10元/⽄得某种⽔果,经过两次降价后得价格为8、1元/⽄,并且两次降价得百分率相同.(1)求该种⽔果每次降价得百分率;(2)从第⼀次降价得第1天算起,第x 天(x 为正数)得售价、销量及储存与损耗费⽤得相关信息如表所⽰、已知该种⽔果得进价为4、1元/⽄,设销售该⽔果第x (天)得利润为y (元),求y 与x (1≤x ＜15)之间得函数关系式,并求出第⼏天时销售利润最⼤？(3)在(2)得条件下,若要使第15天得利润⽐(2)中最⼤利润最多少127、5元,则第 15天在第14天得价格基础上最多可降多少元？6、(2018湖北荆州)某玩具⼚计划⽣产⼀种玩具熊猫,每⽇最⾼产量为40只,且每⽇产出得产品全部售出,已知⽣产x 只玩具熊猫得成本为R(元),售价每只为P(元),且R 、P 与x 得关系式分别为R x =+50030,P x =-1702。

初中数学极值问题解答探究

显然，当x=l O时，即甲店运A村10吨时，运费最少
为96 0元，但A村只要9 吨i
．‘．当x·大：9时，答：略
Ym4、=1000元
例4．现用12m长的竹篱笆丽成一个矩形鸡场。 ( 1) 若不借助任何障碍物嗣成鸡场，则鸡场面积最大为多少?( 2) 若借助长5米的墙为一边围成鸡场，求此鸩场面积最大为多少? 分析：这种题型多见于九年级下册教材及相关资料上。此时学生已掌握二次函数相应知识，运用二次函数性质及图象求解较为方便。解：( 1) 若不借助障碍设围成鸡场长xm，面积为 ym2，则
二、非负数“a2≥0”的运用
例2．某服装店销售一种进价为30 元一件的女式衬衫，由以往销售情况可知售价为60元每天可售出
40 件。为了减少库存获得更大利润，该店决定采取降
价措施，经市场调查发现，这种衬衫每降价4元，每天
就可多售8件。试求每件衬衫应降价多少元该服装店
垦
校一
座晦I 初中数学酗极值问题啊解麓嬲
。师宗县瓦鲁学校邢海青
随着数学教学改革的深化，学生获取知识的途
径以及在日常生活中的运用倍受关注．数学考试也
进一步贴近生活实际，特别是在平面图形、代数计算
和函数思想等方面更接近Et 常生活。为准确地解决
生活实际问题寻找可靠的数学依据，本文就数学中
考中经常出现的上述三方面试题作简要分析探究，
吨
解：设甲店运至A村x吨，所需总运费Y元，则甲店运至B村( 10一x ) 吨，乙店运至A村、B村的氮肥分别为
( 9-x) 吨、8- (9一X) 吨即( x- 1) 吨，于是：
y=50x+70( 10—x) +80( 9一x) +60( x—1)

初中数学中求极值的几种常见的方法

初中数学中求最值的几种常见方法仪陇县实验学校李洪泉在生活实践中，人们经常面对求最值的问题：如在一定方案中，往往会讨论什么情况下花费最低、消耗最少、产值最高、获利最大等；在解数学题时也常常求某个变量的最大值或最小值。

同时，探求最值也是中考或一些高中学校自主招生考试中的一个热点内容，是初高中知识衔接的重要内容。

这类问题涉及变量多，综合性强，技巧性强，要求学生要有较强的数学转化思想和创新意识。

下面从不同的角度讨论如何求一些问题的最值。

一、根据绝对值的几何意义求最值实数的绝对值具有非负性，a0 ，即 a 的最小值为0，但根据绝对值的代数意义求一些复杂问题的最值就要采用分类讨论法，比较麻烦。

若根据绝对值的几何意义求最值就能够把一些复杂的问题简单化。

例 1：已知 M x 1x 3 ，则M的最小值是。

【思路点拨】用分类讨论法求出x 1x 3 的最小值是4, 此时 3 x 1 。

如果我们从绝对值的几何意义来看此题,就是在数轴上求一点,使它到点 1 和点 3 的距离之和为最短。

显然 ,若x 3 ,距离之和为[1 ( 3)]2( 3 x ) 4 ;若 3 x 1 ,距离之和为 1 ( 3) 4 ;若 x 1 ,距离之和为[1 ( 3)] 2( x 1) 4 。

所以,当 3 x 1 时,距离之和最短,最小值为4。

故M的最小值为 4。

二、利用配方法求最值完全平方式具有非负性，2 2即 ( a b ) 0 。

一个代数式若能配方成 m ( a b )k 的形式，则这个代数式的最小值就为k 。

例 2：设a , b为实数，求a2 ab b2 a 2 b 的最小值。

【思路点拨】一是将原式直接配方成与 a , b 的完全平方式有关的式子可以求出最小值。

二是引入参数设 a 2 ab b 2 a 2b t ，将等式整理成关于 a 的二次方程，运用配方法利用判别式求最值。

解： (方法一 ) 配方得：2ab2a 2 ba b2(b 1) a22 ba b( a b 1 )2 3 b2 3 b 12 4 2 4 ( ab 1 2 3 21 12) ( b 1)4b 10, b 1 0, 即 a 0, b 1 时，上式中不等号的等式成立，故所求的最小值当 a2为 1 。

初中数学最值问题解题策略与技巧

初中数学最值问题解题策略与技巧【摘要】初中数学最值问题是数学中常见且重要的题型，解题需要掌握一定的策略和技巧。

本文从理解最大值和最小值的定义开始，逐步介绍如何寻找函数的极值点、应用导数求解最值问题、利用比较法解决最值问题以及考虑约束条件的最值问题。

通过对这些策略和技巧的学习和实践，可以帮助初中生更好地解决各种最值问题。

在结尾部分，总结了初中数学最值问题解题的关键方法，并强调了通过不断练习来提高解题能力的重要性。

通过本文的学习，读者可以更加熟练地解决各种复杂的最值问题，从而提高数学解题的能力和水平。

【关键词】初中数学、最值问题、解题策略、技巧、最大值、最小值、定义、函数、极值点、导数、比较法、约束条件、练习、提高能力。

1. 引言1.1 初中数学最值问题解题策略与技巧在学习初中数学时，最值问题是一个常见且重要的题型。

解决最值问题需要一定的技巧和策略，只有掌握了正确的方法才能高效地解题。

要理解最大值和最小值的定义。

最大值指的是函数取得的最大数值，最小值则是函数取得的最小数值。

在解决最值问题时，要明确函数的最大值和最小值在哪个区间内。

需要寻找函数的极值点。

函数的极值点是指函数在某一区间内取得最大值或最小值的点。

通过求导或者观察函数的图像来找到函数的极值点。

可以应用导数求解最值问题。

通过求导数，可以得到函数的增减性和拐点，从而找到函数的最值点。

还可以利用比较法解决最值问题。

将两个函数进行比较，找到它们的交点，从而确定最值点。

要考虑约束条件的最值问题。

有时候在解决最值问题时会受到一些条件的限制，需要将这些条件考虑进去，综合考虑才能得到最终的解答。

初中数学最值问题需要多方面的考虑和分析，掌握了上述的解题策略和技巧，才能更好地解决这类问题。

不断练习提高解题能力也是非常重要的。

通过不断练习，可以更加熟练地运用这些方法，提高解题的效率和准确度。

希望同学们能够认真学习和掌握这些技巧，更好地应对各类最值问题。

2. 正文2.1 理解最大值和最小值的定义最大值和最小值是数学中常见的概念，在解决最值问题时，首先需要理解它们的定义。

初中数学最值问题汇总

初中数学最值问题汇总
初中数学中的最值问题主要涉及以下几种类型：
1、最大值和最小值：在给定条件下，求某个变量的最大值或最小值。

2、最佳选择问题：在多种选择中，通过比较各种情况的成本或收益，选择最优的方案。

3、图形中的最值问题：在图形中求某一点或某一段的最值，如圆、抛物线、三角形等。

以下是一些常见的最值问题及解决方法：
1、配方法：对于二次函数，通过配方将函数转化为顶点式，从而容易求出最大值或最小值。

2、轴对称：对于线段和直线的问题，常常通过轴对称找到最短路径或最小值。

3、均值不等式：在求几个数的和的最小值时，常常使用均值不等式。

4、函数的单调性：利用函数的单调性来求解最值问题。

此外，还有如利用导数求解最值、概率统计中的最值问题等。

在解决最值问题时，需要灵活运用各种数学知识和方法。

初二数学上册综合算式专项练习题之解简单函数极值

初二数学上册综合算式专项练习题之解简单函数极值简单函数极值是初中数学中的一个重要概念，它对于我们理解函数的性质和解决实际问题都非常有帮助。

本文将通过解题的方式，介绍初二数学上册综合算式专项练习题中的一些简单函数极值问题，并给出详细的解析。

问题1：已知函数f(x) = -2x^2 + 4x + 3，求f(x)的极值点及对应的最大值或最小值。

解析：首先，我们需要求出f(x)的导函数f'(x)。

由于f(x) = -2x^2 + 4x + 3，所以f'(x) = -4x + 4。

接下来，我们令f'(x) = 0，求出极值点。

-4x + 4 = 0得到x = 1。

将x = 1代入f(x)计算，得到f(1) = 5。

所以，极值点为x = 1，对应的最大值为f(1) = 5。

问题2：已知函数g(x) = x^2 - 6x + 5，求g(x)的极值点及对应的最大值或最小值。

解析：同样地，我们需要求出g(x)的导函数g'(x)。

由于g(x) = x^2 - 6x + 5，所以g'(x) = 2x - 6。

令g'(x) = 0，求出极值点。

2x - 6 = 0得到x = 3。

将x = 3代入g(x)计算，得到g(3) = -1。

所以，极值点为x = 3，对应的最小值为g(3) = -1。

通过以上两个例题，我们可以总结出解简单函数极值问题的一般步骤。

步骤一：求函数的导函数。

首先，我们需要将给定的函数关于自变量求导，得到函数的导函数。

导函数的零点即为函数的极值点。

步骤二：设置导函数等于零，求出极值点。

我们令导函数等于零，即f'(x) = 0或g'(x) = 0，通过求解方程，可以得到极值点的横坐标。

步骤三：将极值点代入原函数，求出对应的最大值或最小值。

将求得的极值点代入原函数，即f(x)或g(x)，计算得到最大值或最小值。

需要注意的是，以上步骤适用于求解简单函数的极值问题，对于复杂的函数可能需要更复杂的方法。

初中数学极值问题

初中数学中求极值的几种常见的方法

初中数学100道最值问题经典

初中数学,隐圆与极值问题经典题型.doc

中学生求极值的方法

初中数学最值问题六种模型

初中最值问题的常用解法及模型

中学数学 利用导数研究函数的极值和最值(含答案)

初中数学常见8种最值问题

初中数学中求函数极值的常用解法举例

初中数学中的极值习题

初三数学中考专题极值问题

初中数学最值问题专题

初中数学极值问题解答探究

初中数学中求极值的几种常见的方法

初中数学最值问题解题策略与技巧

初中数学最值问题汇总

初二数学上册综合算式专项练习题之解简单函数极值

中学数学利用导数研究函数的极值和最值(含答案)