广州一模(最清晰版)
2024广东省广州市天河区中考一模数学试题含答案解析

2024届初三毕业班综合测试数学本试卷共三大越25小题,共4页,满分120分.考试时间120分钟注意事项:1.答卷前,考生必须用黑色字迹的钢笔或签字笔将自己的学校、姓名、班级、座位号和考生号填写在答题卡相应的位置上,再用2B 铅笔把考号的对应数字涂黑.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案;不能答在试卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔或涂改液.不按以上要求作答的答案无效.4.考生必须保证答题卡的整洁,考试结束后,将试卷和答题卡一并交回.一、选择题(本题有10个小题,每小题3分,满分30分,每小题给出的四个选项中.只有一个是正确的)1. 如图,数轴上点A 所表示的数的相反数为( )A. 3−B. 3C. 13−D. 13【答案】A【解析】【分析】通过识图可得点A 所表示的数为3,然后结合相反数的概念求解.【详解】解:由图可得,点A 所表示的数为3,∴数轴上点A 所表示的数的相反数为-3,故选:A .【点睛】本题考查了数轴上的点击相反数的概念,准确识图,理解相反数的定义是解题关键. 2. 据国家统计局公布,2023年第一季度,全国居民人均可支配收入10870元.数据10870用科学记数法表示为( )A. 41.08710×B. 410.8710×C. 310.8710×D. 31.08710× 【答案】A【解析】【分析】用科学记数法表示较大的数的一般形式为10n a ×,其中110a ≤<,n 等于原数的整数位数减1,即可得到答案.【详解】解:用科学记数法表示较大的数的一般形式为10n a ×,其中110a ≤<,n 等于原数的整数位数减1,∴410870 1.08710=×,故答案选:A .【点睛】本题考查了科学记数法,掌握科学记数法的表示方法是解题的关键.3. 下列几何体中,各自的三视图完全一样的是( ).A. B. C. D.【答案】D【解析】【分析】本题主要考查了常见的几何体的三视图,熟知常见几何体的三视图是解题的关键.【详解】解:A 、俯视图是三角形,主视图是长方形,左视图是长方形,中间有一条竖直实线,不符合题意;B 、俯视图是一个圆,左视图和主视图都是等腰三角形,不符合题意;C 、俯视图是一个圆,左视图和主视图都是长方形,不符合题意;D 、主视图,俯视图,左视图都是圆,符合题意;故选:D .4. 下列运算正确的是( )A. ()2211m m −=−B. ()3326m m =C. 734m m m ÷=D. 257m m m +=【答案】C【解析】【分析】根据幂的运算法则,完全平方公式处理.【详解】解:A. ()22121m m m −=−+,原运算错误,本选项不合题意;B. ()3328m m =,原运算错误,本选项不合题意;C. 734m m m ÷=,符合运算法则,本选项符合题意;D. 25m m +,不能进一步运算化简,原运算错误,本选项不合题意;故选:C .【点睛】本题考查乘法公式在整式乘法中的运用,幂的运算法则,掌握相关法则和公式是解题的关键. 5. 一组数据:3,4,4,4,5,若去掉一个数据4,则下列统计量中发生变化的是( )A. 众数B. 中位数C. 平均数D. 方差【答案】D【解析】【分析】根据众数、中位数、平均数及方差可直接进行排除选项.【详解】解:由题意得: 原中位数为4,原众数为4,原平均数为3444545x ++++==,原方差为()()()()()2222223444444454255S −+−+−+−+− =; 去掉一个数据4后的中位数为4442+=,众数为4,平均数为344544x +++==,方差为()()()()2222234444454142S −+−+−+− =;∴统计量发生变化的是方差;故选D .【点睛】本题主要考查平均数、众数、众数及方差,熟练掌握求一组数据的平均数、众数、众数及方差是解题的关键.6. 某运输公司运输一批货物,已知大货车比小货车每辆多运输5吨货物,且大货车运输75吨货物所用车辆数与小货车运输50吨货物所用车辆数相同,设有大货车每辆运输x 吨,则所列方程正确的是( ) A 75505x x =− B. 75505x x =− C. 75505x x =+ D. 75505x x =+ 【答案】B【解析】【分析】根据“大货车运输75吨货物所用车辆数与小货车运输50吨货物所用车辆数相同”即可列出方程.【详解】解:设有大货车每辆运输x 吨,则小货车每辆运输()5x −吨,则75505x x =−. 故选B【点睛】本题考查分式方程应用,理解题意准确找到等量关系是解题的关键..的7. 下列四个函数图象中,当x <0时,函数值y 随自变量x 的增大而减小的是( )A. B. C. D.A. 55.5mB. 【答案】D【解析】【详解】A 、根据函数的图象可知y 随x 的增大而增大,故本选项不符合题意;B 、根据函数的图象可知在第二象限内y 随x 的增大而减增大,故本选项不符合题意;C 、根据函数的图象可知,当x <0时,在对称轴的右侧y 随x 的增大而减小,在对称轴的左侧y 随x 的增大而增大,故本选项不符合题意;D 、根据函数的图象可知,当x <0时,y 随x 的增大而减小;故本选项符合题意.故选 D .【点睛】本题考查了函数的图象,函数的增减性,熟练掌握各函数的性质是解题的关键.8. 如图,小亮为了测量校园里教学楼AB 的高度,将测角仪CD 竖直放置在与教学楼水平距离为的地面上,若测角仪的高度为1.5m ,测得教学楼的顶部A 处的仰角为30 ,则教学楼的高度是( )54m C. 19.5m D. 18m【答案】C【解析】 【分析】过D 作DE AB ⊥交AB 于E ,得到DE ,在Rt ADE △中,tan 30AE DE=o ,求出AE ,从而求出AB 【详解】过D 作DE AB ⊥交AB 于E ,DE BC ==Rt ADE △中,tan 30AE DE =o18m AE ∴= 18 1.519.5m AB ∴=+=在故选C【点睛】本题主要考查解直角三角形,能够构造出直角三角形是本题解题关键9. 如图,O 是ABC 的外接圆,且AB AC =,30BAC ∠=°,在 AB 上取点D (不与点A ,B 重合),连接BD ,AD ,则BAD ABD ∠+∠的度数是( )A. 60°B. 105°C. 75°D. 72°【答案】C【解析】 【分析】连接CD ,根据题意,得,BAD BCD ABD ACD ∠=∠∠=∠,结合AB AC =,30BAC ∠=°,得到180752−=°∠∠=°BAC ACB ,计算BAD ABD ∠+∠即可,本题考查了圆周角定理,等腰三角形的性质,熟练掌握圆周角定理,等腰三角形的性质是解题的关键.【详解】连接CD ,根据题意,得,BAD BCD ABD ACD ∠=∠∠=∠, ∵AB AC =,30BAC ∠=°, ∴180752−=°∠∠=°BAC ACB , ∴75BAD ABD BCD ACD ACB ∠+∠=∠+∠=∠=°,故选C ..10. 如图,M 是ABC 三条角平分线的交点,过M 作DE AM ⊥,分别交AB 、AC 于点D 、E 两点,设BD a =,DE b =,CE c =,关于x 的方程()210ax b x c +++=的根的情况是( )A. 一定有两个相等的实数根B. 一定有两个不相等的实数根C. 有两个实数根,但无法确定是否相等D. 没有实数根【答案】B【解析】 【分析】M 是ABC 三条角平分线的交点,过M 作DE AM ⊥,则得出BDM MEC BMC ∠=∠=∠,即可得出DBM MBC ∽,再求出BMC MEC ∽,DBM EMC ∽,即可得出:214ac b =,即可求解. 【详解】AM 平分BAC ∠,DE AM ⊥, ADM AEM ∴∠=∠,1122MDME DE b ===, 1902BDM MEC BAC ∴∠=∠=°+∠, 1902BMC BAC ∴∠=°+∠, BDM MEC BMC ∴∠=∠=∠,M 是ABC 的内角平分线的交点,∴DBM MBC ∽,同理可得出:BMC MEC ∽,∴DBM EMC ∽, ∴BD MD ME CE=, BD EC MD ME ∴⋅=⋅,即:214ac b =, ∴222(1)421210b ac b b b b ∆=+−=++−=+>,∴关于x 的方程2(1)0ax b x c +++=的根的情况是:一定有两个不相等的实数根.故选:B .【点睛】此题主要考查了根的判别式,相似三角形的判定与性质,根据已知得出BDM MEC BMC ∠=∠=∠是解题关键.二、填空题(本题有6个小题,每小题3分,共18分)11. 方程420x +=的解为______.【答案】2x =−【解析】【分析】根据解方程的基本步骤解答即可,本题考查了解方程的基本步骤,熟练掌握步骤是解题的关键.【详解】420x +=,24x =−,解得2x =−,故答案为:2x =−.12. 因式分解:x 2﹣3x=_____.【答案】x (x ﹣3)【解析】【详解】试题分析:提取公因式x 即可,即x 2﹣3x=x (x ﹣3). 考点:因式分解.13. 现有50张大小、质地及背面图案均相同的《西游记》人物卡片,正面朝下放置在桌面上,从中随机抽取一张并记下卡片正面所绘人物的名字后原样放回,洗匀后再抽.通过多次试验后,发现抽到绘有孙悟空这个人物卡片的频率约为0.3.估计这些卡片中绘有孙悟空这个人物的卡片张数约为____.【答案】15【解析】【详解】因为通过多次试验后,发现抽到绘有孙悟空这个人物卡片的频率约为0.3,则这些卡片中绘有孙悟空这个人物的卡片张数=0.3×50=15(张).所以估计这些卡片中绘有孙悟空这个人物的卡片张数约为15张.故答案为15.14. 已知()1,1P x ,()2,1Q x 两点都在抛物线231y x x =−+上,那么12x x +=________.【答案】3【解析】【分析】根据题意可得点P 和点Q 关于抛物线的对称轴对称,求出函数的对称轴即可进行解答. 【详解】解:根据题意可得:抛物线的对称轴为直线:33222b x a −=−=−=, ∵()1,1P x ,()2,1Q x , ∴12322x x +=, ∴123x x +=. 故答案为:3.【点睛】此题考查了二次函数的性质,解题的关键是根据题意,找到P 、Q 两点关于对称轴对称求解. 15. 如图,平面直角坐标系中,A 与x 轴相切于点B ,作直径BC ,函数()200yx x=>的图象经过点C ,D 为y 轴上任意一点,则ACD 的面积为_______.【答案】5【解析】【分析】本题考查了反比例函数系数k 的几何意义,切线的性质;根据反比例函数系数k 的几何意义可得20OB BC ⋅=,由切线的性质可得BC x ⊥轴,再根据三角形的面积公式列式求解即可.【详解】解:∵点C 在函数()200y x x=>的图象上, ∴20OB BC ⋅=,∵A 与x 轴相切于点B ,∴BC x ⊥轴,∴BC y ∥轴, ∴111205244ACD S AC OB BC OB =???, 故答案为:5.16. 如图,在矩形ABCD 中,6AB =,8AD =,点E ,F 分别是边CD ,BC 上的动点,且90AFE ∠=°.(1)当5BF =时,tan FEC ∠=______; (2)当AED ∠最大时,DE 的长为_______.【答案】 ①.65 ②. 103##133 【解析】【分析】(1)证明90AFB EFC FEC ∠=°−∠=∠,利用tan tan AFB FEC ∠=∠计算即可; (2)当BC 与O 相切时,AFD ∠的值最大,此时, AED ∠也最大,利用三角形相似计算即可.【详解】(1)∵矩形ABCD 中,6AB =,8AD =,∴90,90ABF FCE °°∠=∠=∵90AFE ∠=°,∴90AFB EFC FEC ∠=°−∠=∠,∴6tan tan 5AB AFB FEC BF ∠=∠==, 故答案为:65. (2)如图,取AE 的中点O ,连接,,OD OF DF .∵矩形ABCD 中,6AB =,8AD =,∴90ADE ∠=°,∵90AFE ∠=°,∴A 、D 、E 、F 四点共圆,∴AED AFD ∠=,∴当BC 与O 相切时,AFD ∠的值最大,此时, AED ∠也最大,∴OF BC ⊥,∵矩形ABCD 中,6AB =,8AD =,∴90ADE ABF ∠=∠=°,∴OF AB EC , ∴EO CF OA BF =, ∴142BF CF BC ===, ∵90AFE ∠=°,∵矩形ABCD 中,6AB =,8AD =,∴90,90ABF FCE °°∠=∠=∵90AFE ∠=°,∴90AFB EFC FEC ∠=°−∠=∠,∴AFB FEC ∽△△, ∴BF AB EC FC =, ∴464EC =, ∴83EC =, ∴810633DE CD EC =−=−=, 故答案为:103. 【点睛】本题考查了矩形的性质,正切函数,三角形相似的判定和性质,切线的性质,四点共圆,圆周角定理,熟练掌握正切函数,切线性质,四点共圆是解题的关键.三、解答题(本大题有9小题,共7分,解答要求写出文字说明,证明过程或计算步骤)17. 解不等式:6327x x −>−.【答案】1x −>【解析】【分析】按照解不等式的基本步骤解答即可.本题考查了解不等式,熟练掌握解题的基本步骤是解题的关键.【详解】6327x x −−>,移项,得6237x x −−>合并同类项,得44x −>,系数化为1,得1x −>.18. 如图,四边形ABCD 中,AB DC =,AB DC ,E ,F 是对角线AC 上两点,且AE CF =.求证:ABE CDF △≌△.【答案】见解析【解析】【分析】本题考查了平行线的性质,三角形全等的判定,熟练掌握判定定理是解题的关键.根据AB DC 得BAE DCF ∠=∠,证明即可.【详解】∵AB DC ,∴BAE DCF ∠=∠,在ABE 和CDF 中AB DC BAE DCF AE CF = ∠=∠ =∴ABE CDF △≌△.19. 为打造书香文化,培养阅读习惯,某中学计划在各班建设图书角,并开展主题为“我最喜欢阅读的书篇”的调查活动,学生根据自己的爱好选择一类书籍(A :科技类,B :文学类,C :政史类,D :艺术类,E :其他类).张老师组织数学兴趣小组对学校部分同学进行了问卷调查.根据收集到的数据,绘制了两幅不完整的统计图(如图所示).根据图中信息,请回答下列问题:(1)填空:参与本次问卷调查活动的学生人数是______;(2)甲同学从A ,B ,C 三类书籍中随机选择一种,乙同学从B ,C ,D 三类书籍中随机选择一种,请用画树状图或者列表法求甲乙两位同学选择相同类别书籍的概率.【答案】(1)50 (2)29【解析】【分析】(1)根据样本容量=频数÷所占百分数,求得样本容量后,计算解答.(2)利用画树状图计算即可.本题考查了条形统计图、扇形统计图,画树状图求概率,熟练掌握统计图的意义,准确画树状图是解题的关键.【小问1详解】∵4?8%50÷=(人),故答案为:50.【小问2详解】画树状图如下:共有9种等可能的结果,其中抽到相同类有2种可能的结果,∴相同的概率为:29. 20. 已知关于x 的函数()31111m m y x m m m +=+≠−++图象经过点()1,A m n −. (1)用含m 的代数式表示n ;(2)当m =k y x=的图象也经过点A ,求k 的值. 【答案】(1)1nm =+ (2)4【解析】【分析】(1)把点的坐标代入解析式,化简计算即可;(2)当m =)1A +,代入解析式,计算即可. 本题本题考查了反比例函数与点的关系,熟练掌握这些知识是解题的关键.【小问1详解】 解:根据题意,得()()213111111m m m n m m m m m ++=×−+==++++. 【小问2详解】解:当m =时,此时点)1A −+,故)11514k =+=−=. 21. 如图,在ABC 中,90ABC ∠=°,60A ∠=°,3AB =.(1)尺规作图:在BC 上找一点P ,作P 与AC ,AB 都相切,与AC 的切点为Q ;(保留作图痕迹) (2)在(1)所作的图中,连接BQ ,求sin CBQ ∠的值.【答案】(1)见解析 (2)1sin 2CBQ ∠= 【解析】【分析】(1)结合切线的判定与性质,作BAC ∠的平分线,交BC 于点P ,以点P 为圆心,PB 的长为半径画圆即可.(2)由题意可得Rt Rt ABP AQP △≌△,则AB AQ =,可得ABQ 为等边三角形,即60ABQ ∠=°,则30CBQ ∠=°,进而可得答案.【小问1详解】解:如图,作BAC ∠的平分线,交BC 于点P ,以点P 为圆心,PB 的长为半径画圆,交AC 于点Q , 则P 即为所求.;【小问2详解】解:由(1)可得,BP PQ =,PQ AC ⊥,90AQP ∴∠=°,AP AP = ,()Rt Rt HL ABP AQP ∴ ≌,AB AQ ∴=,60BAC ∠=° ,ABQ ∴ 为等边三角形,60ABQ ∴∠=°,30CBQ ∴∠=°,1sin sin 302CBQ ∴∠=°=. 【点睛】本题考查作图—复杂作图、切线的判定与性质、等边三角形的性质、特殊角的三角函数值等知识点,熟练掌握相关知识点是解答本题的关键.22. 如图是气象台某天发布的某地区气象信息,预报了次日0时至8时气温随着时间变化情况,其中0时至5时的图象满足一次函数关系式y kx b =+,5时至8时的图象满足函数关系式21660y x x =−+−.请根据图中信息,解答下列问题:(1)填空:次日0时到8时的最低气温是______;(2)求一次函数y kx b =+解析式; (3)某种植物在气温0℃以下持续时间超过4小时,即遭到霜冻灾害,需采取预防措施.请判断次日是否的需要采取防霜措施,并说明理由.【答案】(1)5−℃(2)835y x =−+ (3)需要采取防霜措施,见解析【解析】【分析】(1)根据题意,当5x =时,函数最小值,代入解析式21660y x x =−+−计算即可.(2)把()()0,3,5,5−分别代入y kx b =+中,计算即可; (3)令0y kx b =+=,216600y x x =−+−=,计算交点坐标的横坐标的差,对照标准判断即可. 本题考查了待定系数法,图象信息识读,图象与x 轴交点坐标的计算,熟练掌握待定系数法,交点坐标的计算是解题的关键.【小问1详解】根据题意,当5x =时,函数有最小值,代入解析式21660y x x =−+−得,2580605y =−+−=−,故答案为:5−℃.【小问2详解】把()()0,3,5,5−分别代入y kx b =+中, 得553k b b +=− = , 解得853k b =− = , ∴835y x =−+. 【小问3详解】 令0835y x =−+=, 解得158x =; 令216600y x x =−+−=,解得126,10x x ==(舍去), 故()156 4.125h 8−=, ∵4.1254>∴遭到霜冻灾害,故需要采取防霜措施.23. 在初中物理中我们学过凸透镜的成像规律.如图MN 为一凸透镜,F 是凸透镜的焦点.在焦点以外的主光轴上垂直放置一小蜡烛AB ,透过透镜后呈的像为CD .光路图如图所示:经过焦点的光线AE ,通过透镜折射后平行于主光轴,并与经过凸透镜光心的光线AO 汇聚于C 点.(1)若焦距4OF =,物距6OB =.小蜡烛高度1AB =,求蜡烛的像CD 的长度;(2)设OB x OF =,AB y CD=,求y 关于x 的函数关系式,并通过计算说明当物距大于2倍焦距时,呈缩小的像.【答案】(1)2米 (2)1y x =−,说明见解析【解析】【分析】本题主要考查了相似三角形的实际应用,平行四边形的性质与判定;(1)先证明ABF EOF ∽,利用相似三角形的性质得到2OE =,再证明四边形OECD 是平行四边形,可得2CD OE ==米;(2)由(1)得ABF EOF ∽,2CD OE ==,则AB OB OF CD OF −=,据此可得1y x =−,当2OB OF>,即2x >时,11y x =−>,据此可得结论. 【小问1详解】解:由题意得,AB OE ∥,∴ABF EOF ∽, ∴AB BF OE OF =,即1644OE −=, ∴2OE =,∵OE CD CE OD ∥,∥,的∴四边形OECD 是平行四边形,∴2CD OE ==米,∴蜡烛的像CD 的长度为2米;【小问2详解】解:由(1)得ABF EOF ∽,2CD OE == ∴AB BF OE OF =,即AB OB OF CD OF−=, ∴1y x =−, 当2OB OF >,即2x >时,11y x =−>, ∴1AB CD>,即AB CD >, ∴物高大于像高,即呈缩小的像.24. 矩形ABCD 中,4AB =,8BC =.(1)如图1,矩形的对角线AC ,BD 相交于点O .①求证:A ,B ,C ,D 四个点在以O 为圆心的同一个圆上;②在O 的劣弧AD 上取一点E ,使得AE AB =,连接DE ,求AED △的面积.(2)如图2,点P 是该矩形的边AD 上一动点,若四边形ABCP 与四边形GHCP 关于直线PC 对称,连接GD ,HD ,求GDH 面积的最小值.【答案】(1)①见解析;②485(2)8【解析】【分析】(1)①根据矩形的性质,得到90ABC ∠=°,得到点A ,B ,C 在以O 为圆心,OA 为半径的圆上,根据矩形的性质,得OA OB OC OD ===,判定点D 在以O 为圆心的同一个圆上,继而得到四点共圆;②过点E 作在EG AD ⊥于点D ,根据AE AB =,得到ADE ADB ∠=∠,结合4AE AB ==,8BC =,得到1tan tan 2AB EG ADE ADB BC GD ∠=∠===,设2EG x GD x ==,,则82AG AD GD x =−=−,利用勾股定理计算x ,利用面积公式解答即可.(2)根据折叠的性质,得到8,4,90CB CH BA HG CHG ====∠=°,根据CH CD DH ≤+,得到4DH CH CD −=≥,当点C ,D ,H 三点共线时,4DH =最小,此时GDH 面积的为1144822GH DH ×=××=,最小. 【小问1详解】①∵矩形ABCD ,∴90ABC ∠=°,OA OB OC OD ===,∴点A ,B ,C 在以O 为圆心,OA 为半径的圆上,∵OA OB OC OD ===,∴点D 在以O 为圆心的同一个圆上,故A ,B ,C ,D 四个点在以O 为圆心的同一个圆上;②如图,过点E 作在EG AD ⊥于点D ,∵AE AB =,∴ADE ADB ∠=∠,∵4AE AB ==,8BC =, ∴1tan tan 2AB EG ADE ADB BC GD ∠=∠===, 设2EG x GD x ==,,则82AG AD GD x =−=−, ∴()228216x x −+=, 解得12,45x x ==(舍去), ∴AED △的面积112488255××=. 【小问2详解】根据折叠的性质,得到8,4,90CB CH BA HG CHG ====∠=°, ∵CH CD DH ≤+,∴4DH CH CD −=≥,∴当点C ,D ,H 三点共线时,4DH =最小,此时GDH 面积的为1144822GH DH ×=××=,最小.【点睛】本题考查了矩形的性质,构造辅助圆,正切函数,勾股定理,三角形不等式,熟练掌握正切函数,辅助圆,勾股定理,三角形不等式是解题的关键.25. 已知抛物线()21:1C y a x h =−−,直线()2:1l y k x h =−−,其中02a ≤<,0k >. (1)求证:直线l 与抛物线C 至少有一个交点;(2)若抛物线C 与x 轴交于()1,0A x ,()2,0B x 两点,其中12x x <,且121033x x <+<,求当1a =时,抛物线C 存在两个横坐标为整数的顶点;(3)若在直线l 下方的抛物线C 上至少存在两个横坐标为整数的点,求k 的取值范围.【答案】(1)见解析 (2)()()1,1,2,1−−(3)4k >【解析】【分析】(1)联立()()211y a x h y k x h =−− =−− ,解方程,判断方程的解得个数即可解答;(2)根据1a =时,()21:1C y x h =−−,结合抛物线C 与x 轴交于()1,0A x ,()2,0B x 两点,结合12x x <,则12,11x h x h ==+−,且121033x x <+<,求得11124h <<,确定h 的整数解有1,2两个,得证.(3)根据题意,得当2x h =+时,21y y >恒成立.建立不等式解答即可.本题考查了抛物线与一次函数的综合,不等式组的解集与整数解,熟练掌握抛物线的性质是解题的关键.【小问1详解】联立()()211y a x h y k x h =−− =−−, 解方程,得,ah k x h x a+==, 当x h =时,1y =−,即直线与抛物线恒过点(),1h −,故直线l 与抛物线C 至少有一个交点.【小问2详解】当1a =时,()21:1C y x h =−−,∵抛物线C 与x 轴交于()1,0A x ,()2,0B x 两点, ∴1x h −=±,∵12x x <, ∴12,11x hx h ==+−, ∵121033x x <+<, ∴420333h <−< 解得11124h <<, ∵h 时整数,∴1,2h h ==, 故抛物线C 存在两个横坐标为整数的顶点,且顶点坐标为()()1,1,2,1−−.【小问3详解】.∵如图所示:由(1)可知:抛物线C 与直线l 都过点(),1A h −.当02a ≤<,0k >,在直线l 下方的抛物线C 上至少存在两个横坐标为整数点, 即当2x h =+时,21y y >恒成立.故()()22121k h h a h h +−−+−−>,整理得:2k a >.又∵2k a >,∴024a <<,∴4k >.。
2024届广东省广州市普通高中毕业班下学期一模考试语文试题(原卷版)

进行科学研究的时候,我们必需研究各个因素和各个量之间的关系,进行量的关系的计算。当然计算与分析不是什么神秘的东西,在农业合作化初期,有些会计不是用黄豆粒的办法来记账吗?所以就是我们一点也不知道高深的数学,用简陋的方法也并不是不可以;这里的问题不是能不能的问题,而是好不好的问题。用简陋的方法,虽然也能进行复杂的计算,但是太花时间,容易出差错;用高效能的方法就能节省时间,少出差错。那么什么是高效能的计算方法呢?那自然是要充分利用了数学的成果才能得到的。所以我们一方面不过高地估计数学方法,它不过是我们计算中的工具;我们另一方面也十分重视数学方法,因为它是一个非常有效的研究工具。
2024年广州市普通高中毕业班综合测试(一)
语文
本试卷共10页,23小题,满分150分。考试用时150分钟。
注意事项:
1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名、考生号、试室号、座位号填写在答题卡上。用2B铅笔将试卷类型(A)填涂在答题卡的相应位置上,并在答题卡相应位置上填涂考生号。
2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
2024年广东省广州市白云区中考数学一模试卷及答案解析
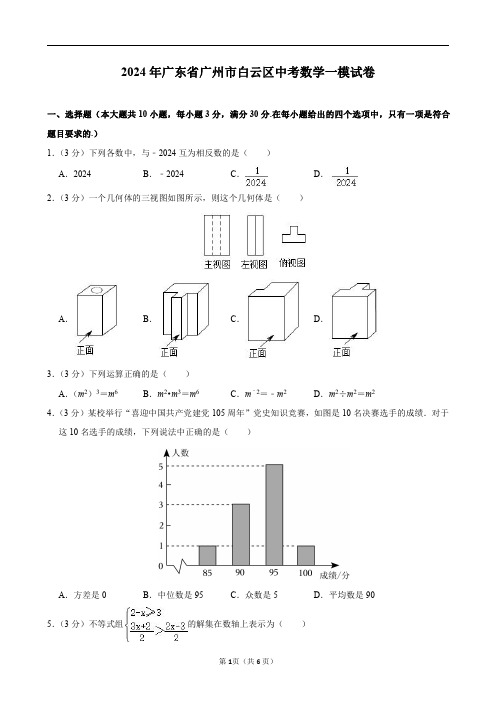
2024年广东省广州市白云区中考数学一模试卷一、选择题(本大题共10小题,每小题3分,满分30分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(3分)下列各数中,与﹣2024互为相反数的是()A.2024B.﹣2024C.D.2.(3分)一个几何体的三视图如图所示,则这个几何体是()A.B.C.D.3.(3分)下列运算正确的是()A.(m2)3=m6B.m2•m3=m6C.m﹣2=﹣m2D.m2÷m2=m24.(3分)某校举行“喜迎中国共产党建党105周年”党史知识竞赛,如图是10名决赛选手的成绩.对于这10名选手的成绩,下列说法中正确的是()A.方差是0B.中位数是95C.众数是5D.平均数是905.(3分)不等式组的解集在数轴上表示为()A.B.C.D.6.(3分)已知一次函数y=ax+b经过点(﹣2,﹣3),正比例函数y1=ax不经过第三象限,则反比例函数的图象位于()A.第一、第二象限B.第一、第三象限C.第二、第三象限D.第二、第四象限7.(3分)喜迎二十大,“龙舟故里”赛龙舟,小亮在龙舟竞渡中心广场点P处观看400米直道竞速赛,如图所示,赛道AB为东西方向,赛道起点A位于点P的北偏西30°方向上,终点B位于点P的北偏东60°方向上,AB=400米,求点P到赛道AB的距离()(结果保留整数,参考数据:)A.B.C.87D.1738.(3分)某校组织540名学生去外地参观,现有A,B两种不同型号的客车可供选择.在每辆车刚好满座的前提下,每辆B型客车比每辆A型客车多坐15人,单独选择B型客车比单独选择A型客车少租6辆.设A型客车每辆坐x人,根据题意可列方程()A.﹣=6B.﹣=6C.﹣=6D.﹣=69.(3分)如图,△ABC的内切圆⊙I与BC,CA,AB分别相切于点D,E,F,若⊙I的半径为r,∠FDE =α,则(AF+CD﹣AC)的值和∠A的大小分别为()A.0,180°﹣2αB.r,180°﹣αC.D.10.(3分)若,则关于x的方程x2﹣(2k﹣2)x+k2﹣1=0根的情况是()A.无实数根B.有两个相等的实数根C.有两个实数根D.有两个不相等的实数根二、填空题(本大题共6小题,每小题3分,满分18分.)11.(3分)2023年10月26日上午,神舟十七号载人飞船载着杨洪波、唐胜杰、江新林3名航天员奔赴“天宫”,从2003年的神舟五号到2023年的神舟十七号,20年中国载人航天工程共有20位航天员问鼎苍穹,截止到目前为止,我国航天员在太空的时间已累计达到近21200个小时,其中,数字21200用科学记数法表为.12.(3分)若点A(﹣1,y1),B,C(2,y3)在抛物线y=(x﹣2)2+k上,则y1,y2,y3的大小关系为(用“>”连接).13.(3分)2023年5月30日是第7个全国科技工作者日,某中学举行了科普知识手抄报评比活动,共有100件作品获得一、二、三等奖和优胜奖,根据获奖结果绘制如图所示的条形图若将获奖作品按四个等级所占比例绘制成扇形统计图,则“二等奖”对应扇形的圆心角度数为°.14.(3分)如图,正方形ABCD的边长为4,点E在边BC上,F为对角线BD上一动点,连接CF,EF,若CF+EF的最小值,则CE=.15.(3分)如图,已知AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,四边形AEDF 的面积为60,DF=5,则△ADE中AD边上的高为.16.(3分)如图,矩形ABCD中,AB=9,AD=12,点P从A出发以每秒3个单位长度的速度沿A→D→C→B→A运动一周到点A停止.当点P不与矩形ABCD的顶点重合时,过点P作直线PQ⊥AP,与矩形的边的另一交点为Q.若点P的运动时间为t,当8<t<10时,CQ长度的范围是.三、解答题(本大题共9小题,满分72分.解答应写出文字说明、证明过程或演算步骤.)17.(4分)解方程:x2+4x﹣12=0.18.(4分)已知:如图,在Rt△ABC中,∠ACB=90°,过点C作CD⊥AB,垂足为D.在射线CD上截取CE=CA,过点E作EF⊥CE,交CB的延长线于点F.求证:BC=FE.19.(6分)如图,在平面直角坐标系xOy中,点A(﹣2,0),所在圆的圆心为O,∠AOB=60°.将AB向右平移5个单位,得到(点A平移后的对应点为C).(1)点B的坐标是,所在圆的圆心坐标是;(2)在图中画出,求的长.20.(6分)给出6个整式:x+2,x﹣2,2x+1,2,x2+x﹣1,x2﹣x﹣11.(1)从上面的6个整式中选择2个合适的整式,组成一个分式;(2)从上面的6个整式中选择2个合适的整式进行乘法运算,使运算结果为一个不含有一次项的多项式,请你列出算式,并写出运算过程.21.(8分)甲、乙、丙三人各自随机选择到A,B两个献血站进行爱心献血.求这三人在同一个献血站献血的概率.22.(10分)某车间甲、乙两台机器共生产9200个零件,两台机器同时加工一段时间后,甲机器出现故障,维修一段时间后仍按原来的效率加工,已知甲机器每天加工150个零件,如图是表示未生产零件的个数y(个)与乙机器工作时间x(天)之间的函数图象.(1)乙机器每天加工个零件,甲机器维修了天;(2)求甲机器出现故障以后,未生产零件的个数y(个)与乙机器工作时间x(天)之间的函数关系式.23.(10分)【问题探究】(1)如图①,在四边形ABCD中,∠A=∠B=90°,在AB边上作点E为一点,连接CE,DE,使得CE⊥DE(画出一个点E即可,要求用尺规作图,保留作图痕迹,不要求写作图的证明);(2)如图②,在四边形ABCD中,AD∥BC,BC=CD,∠C=60°,点E为CD上一点,连接AE,BE,∠ABE=60°,试判断AD与CE之间的数量关系,并说明理由;【问题解决】(3)如图③,四边形ABCD是赵叔叔家的果园平面示意图,点E为果园的一个出入口(点E在边CD 上),AE,BE为果园内的两条运输通道(通道宽度忽略不计),经测量,AD∥BC,AB=AE,∠C=∠ABE=45°,AD=150米,赵叔叔计划在△BCE区域内种植某种果树,并沿CE修建一条安全栅栏,为提前做好修建安全栅栏的预算,请你帮赵叔叔计算出CE的长度.24.(12分)已知直线l:y=kx+b(k>0)经过点P(﹣1,2).(1)用含有k的式子表示b;(2)若直线l与x,y轴分别交于A,B两点,△AOB面积为S,求S的取值范围;(3)过点P的抛物线y=(x﹣k)2+n与y轴交点为E,记抛物线的顶点为C,该抛物线是否存在点F 使四边形BPEF为平行四边形?若存在,求此时顶点C的坐标;若不存在,请说明理由.25.(12分)如图,在四边形ABCD中,点N,M分别在边BC,CD上.连接AM,AN,MN,∠MAN=45°.(1)【实践探究】如图①,四边形ABCD是正方形.(Ⅰ)若CN=6,MN=10,求∠CMN的余弦值;(Ⅱ)若tan∠BAN=,求证:M是CD的中点;(2)【拓展】如图②,四边形ABCD是直角梯形,AD∥BC,∠C=90°,CD=12,AD=16,CN=12,求DM的长.2024年广东省广州市白云区中考数学一模试卷参考答案与试题解析一、选择题(本大题共10小题,每小题3分,满分30分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.【分析】直接利用互为相反数的定义分析得出答案.【解答】解:﹣2024的相反数为2024,A选项正确.故选:A.【点评】本题考查了实数的性质,主要利用了互为相反数的定义,对各选项准确化简是解题的关键.2.【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.【解答】解:根据主视图和左视图为矩形可判断出该几何体是柱体,根据俯视图是两个矩形可判断出该几何体为:故选:D.【点评】本题考查由三视图想象立体图形.做这类题时要借助三种视图表示物体的特点,从主视图上弄清物体的上下和左右形状;从俯视图上弄清物体的左右和前后形状;从左视图上弄清楚物体的上下和前后形状,综合分析,合理猜想,结合生活经验描绘出草图后,再检验是否符合题意.3.【分析】直接利用幂的乘方运算法则、同底数幂的乘除运算法则、负整数指数幂的性质分别化简,进而得出答案.【解答】解:A.(m2)3=m6,故此选项符合题意;B.m2•m3=m5,故此选项不合题意;C.m﹣2=,故此选项不合题意;D.m2÷m2=1,故此选项不合题意.故选:A.【点评】此题主要考查了幂的乘方运算、同底数幂的乘除运算、负整数指数幂的性质,正确掌握相关运算法则是解题关键.4.【分析】分别根据众数、中位数、算术平均数以及方差的定义与计算方法判断即可.【解答】解:由题意可知,这10名选手的成绩的众数是95,中位数是=95,平均数是(85×1+90×3+95×5+100×1)=93,方差是[(85﹣93)2+3×(90﹣93)2+5×(95﹣93)2+(100﹣93)2]=16,故选:B.【点评】本题考查条形统计图,中位数,众数,算术平均数以及方差,理解统计图中数量之间的关系是正确计算的前提,掌握中位数、方差的计算方法是得出正确答案的关键.5.【分析】先解出每个不等式的解集,然后即可得到不等式组的解集,再在数轴上表示出其解集即可.【解答】解:,解不等式①,得:x≤﹣1,解不等式②,得:x>﹣5,∴该不等式组的解集为﹣5<x≤﹣1,其解集在数轴上表示如下:故选:A.【点评】本题考查解一元一次不等式组、在数轴上表示不等式组的解集,解答本题的关键是明确解一元一次不等式的方法.6.【分析】根据正比例函数不经过第三象限得到a<0,再根据一次函数y=ax+b经过点(﹣2,﹣3)确定b值的正负,最后确定反比例函数图象的分布即可.【解答】解:∵正比例函数y1=ax不经过第三象限,∴a<0,∵一次函数y=ax+b经过点(﹣2,﹣3),∴b<0,∴反比例函数的图象位于第二、四象限.故选:D.【点评】本题考查了一次函数图象与系数的关系,熟练掌握反比例函数性质是解答本题的关键.7.【分析】过点P作PC⊥AB,垂足为P,设PC=x米,然后分别在Rt△APC和Rt△CBP中,利用锐角三角函数的定义求出AC,BC的长,再根据AB=400米,列出关于x的方程,进行计算即可解答.【解答】解:过点P作PC⊥AB,垂足为C,设PC=x米,在Rt△APC中,∠APC=30°,∴(米),在Rt△CBP中,∠CPB=60°,∴(米),∵AB=400米,∴AC+BC=400,∴,∴,∴PC=173米,∴点P到赛道AB的距离约为173米,故选:D.【点评】本题考查了解直角三角形的应用﹣方向角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.8.【分析】根据题意,可以列出相应的分式方程,从而可以得到哪个选项是正确的.【解答】解:由题意可得:﹣=6,故选:B.【点评】本题考查由实际问题抽象出分式方程,解题的关键是明确题意,找出题目中的等量关系,列出相应的方程.9.【分析】连接IE、IF,根据切线长定理和切线的性质定理得AF=AE,CD=CE,AB⊥IF,AC⊥IE,则AF+CD=AF+CE=AC,所以AF+CD﹣AC=0,而∠FIE=2∠FDE=2α,则∠A=360°﹣∠AEI﹣∠AFI ﹣∠FIE=180°﹣2α,于是得到问题的答案.【解答】解:连接IE、IF,∵△ABC的内切圆⊙I与BC,CA,AB分别相切于点D,E,F,∠FDE=α,∴AF=AE,CD=CE,AB⊥IF,AC⊥IE,∴AF+CD=AF+CE=AC,∴AF+CD﹣AC=AC﹣AC=0,∵∠AEI=∠AFI=90°,∠FIE=2∠FDE=2α,∴∠A=360°﹣∠AEI﹣∠AFI﹣∠FIE=360°﹣90°﹣90°﹣2α=180°﹣2α,故选:A.【点评】此题重点考查三角形的内切圆的定义、切线的性质定理、切线长定理、圆周角定理、四边形的内角和等于360°等知识,正确地作出辅助线是解题的关键.10.【分析】先根据二次根式有意义的条件得到k≤2,再根据二次根式的性质计算得到|k﹣1|=﹣(k﹣1),则利用绝对值的意义得到k≤1,所以k的取值范围为k≤1,接着计算出根的判别式的值得到Δ=﹣8(k ﹣1),从而可判断Δ≥0,然后根据根的判别式的意义可对各选项进行判断.【解答】解:根据题意得2﹣k≥0,解得k≤2,∵,∴|k﹣1|﹣(2﹣k)=﹣1,即|k﹣1|=﹣(k﹣1),∴k﹣1≤0,解得k≤1,∴k的取值范围为k≤1,∵Δ=[﹣(2k﹣2)]2﹣4(k2﹣1)=﹣8(k﹣1)≥0,∴方程有两个实数解.故选:C.【点评】本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与Δ=b2﹣4ac有如下关系:当Δ>0时,方程有两个不相等的实数根;当Δ=0时,方程有两个相等的实数根;当Δ<0时,方程无实数根.也考查了二次根式的化简求值.二、填空题(本大题共6小题,每小题3分,满分18分.)11.【分析】科学记数法的表现形式为a×10n的形式,其中1≤|a|<10,n为整数,确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同,当原数绝对值大于等于10时,n是正数,当原数绝对值小于1时n是负数;由此进行求解即可得到答案.【解答】解:21200=2.12×104,故答案为:2.12×104.【点评】本题主要考查了科学记数法,熟练掌握科学记数法是关键.12.【分析】根据二次函数的性质得到抛物线y=(x﹣2)2+k的开口向上,对称轴为直线x=2,然后根据三个点离对称轴的远近判断函数值的大小.【解答】解:y=(x﹣2)2+k,∵a=1>0,∴抛物线开口向上,对称轴为直线x=2,∵点A(﹣1,y1)离直线x=2的距离最远,C(2,y3)在直线x=2上,∴y1>y2>y3.故答案无:y1>y2>y3.【点评】本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了二次函数的性质.13.【分析】根据直方图中的数据,可以计算出a的值,然后即可计算出“一等奖”对应扇形的圆心角度数.【解答】解:由条形统计图可得,a=100﹣10﹣50﹣10=30,“一等奖”对应扇形的圆心角度数为:360°×=108°,故答案为:108.【点评】本题考查条形统计图、扇形统计图,解答本题的关键是明确题意,利用数形结合的思想解答.14.【分析】连接AF,AE,推出CF+EF的最小值,就是AE的长,再利用勾股定理求出BE,进而求出CE的长.【解答】解:连接AF,AE,∵四边形ABCD是正方形,∴点A与点C关于直线BD对称,∴AF=CF,∴CF+EF=AF+EF≥AE,∵CF+EF的最小值,∴AE=,在Rt△ABE中,∵AB=4,AE=,∴由勾股定理,得BE===2,∴CE=BC﹣BE=4﹣2=2,故答案为:2.【点评】本题考查轴对称﹣最短路线问题,正方形的性质,勾股定理,两点之间线段最短,能将两线段和的最小值用一条线段表示是解题的关键.15.【分析】先证△AED≌△AFD,可得DE=DF=5,已知四边形AEDF的面积为60,可得△ADE的面积,可求得AE、AD的长,再根据面积公式可得△ADE中AD边上的高的长度.【解答】解:∵DE,DF分别是△ABD和△ACD的高,∴∠AED=∠AFD=90°,∵AD是△ABC的角平分线,∴∠EAD=∠FAD,∵AD=AD,∴△AED≌△AFD(AAS),∴DE=DF=5,△AED的面积=△AFD的面积,∵四边形AEDF的面积为60,=30,∴S△ADE=×DE×AE,∵S△ADE∴AE=12,AD==13,∴△ADE中AD边上的高==,故答案为:.【点评】本题考查了角平分线的性质,关键是掌握角平分线的性质以及全等三角形的判定条件.16.【分析】先判断出P点所在位置,连接AQ,根据三角形相似的判定与性质,用t表示出CQ,从而求出DQ,在根据二次函数的最值求出DQ的取值范围,最后根据勾股定理求出AQ的取值范围即可.【解答】解:由题意可知,当t=8时,点P的运动路程为3×8=24,当t=10时,点P的运动路程为3×10=30,∵AD+CD=21,AD+CD+BC=33,∴当8<t<10时,点P在线段BC上,∴CP=3t﹣21,BP=33﹣3t,∵∠APQ=90°,∴∠CPQ +∠APB =90°,∵∠PAB +∠APB =90°,∴∠PAB =∠CPQ ,∴△CPQ ∽△BAP ,∴=,∴CQ =(t ﹣7)(11﹣t )=﹣(t ﹣9)2+4,∵8<t <10,∴3<CQ ≤4.故答案为:3<CQ ≤4.【点评】本题主要考查了勾股定理的应用,结合相似三角形的判定与性质以及二次函数最值问题来解答是本题解题的关键.三、解答题(本大题共9小题,满分72分.解答应写出文字说明、证明过程或演算步骤.)17.【分析】方程左边的多项式利用十字相乘法分解因式,然后利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.【解答】解:分解因式得:(x ﹣2)(x +6)=0,可得x ﹣2=0或x +6=0,解得:x 1=2,x 2=﹣6.【点评】此题考查了解一元二次方程﹣因式分解法,利用此方法解方程时,首先将方程左边化为积的形式,右边化为0,然后利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.18.【分析】根据题意,先得出∠E =∠ACB ,再用两角夹边判定即可.【解答】证明:∵CD ⊥AB ,∴∠A +∠ACD =90°,∵∠ACB =90°,∴∠ACD +∠ECF =90°,∴∠A =∠ECF ,∵EF ⊥CE ,∴∠E =90°,∴∠E =∠ACB ,在△ACB 和△CEF 中,,∴△ACB≌△CEF(ASA),∴BC=FE.【点评】本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定和性质是解题的关键.19.【分析】(1)根据等边三角形的判定与性质可得点B的坐标,根据题意可得所在圆的圆心坐标;(2)由平移的性质画出,再根据弧长公式计算即可.【解答】解:(1)如图,连接OB,AB,作BP⊥OA于点P,∵OA=OB,∠AOB=60°,∴△AOB是等边三角形,∴AB=OA=2,故BP=AB•sin60°==,OP=OA=1,∴点B的坐标是(﹣1,);所在圆的圆心坐标是(0,0).故答案为:(﹣1,),(0,0);(2)如图所示:==.【点评】本题考查了图象的平移、弧长的计算等,掌握平移的性质以及弧长公式是解答本题的关键.20.【分析】(1)根据分式的定义即可写出,答案不唯一;(2)根据多项式乘多项式的运算法则进行运算即可.【解答】解:(1)写出的分式有:等,答案不唯一;(2)从6个整式:x+2,x﹣2,2x+1,2,x2+x﹣1,x2﹣x﹣11中选择2个整式进行乘法运算,使运算结果为一个不含有一次项的多项式:(x+2)(x﹣2)=x2﹣4.【点评】本题考查了分式的定义及整式的混合运算,分式的定义:如果A、B表示两个整式,并且B中含有字母,那么式叫做分式,A叫做分式的分子,B叫做分式的分母.多项式乘多项式法则:先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.21.【分析】首先根据题意画树状图,然后根据树状图即可求得所有等可能的结果和满足条件的结果数,再根据概率公式求解即可.【解答】解:画树状图得:共8种等可能情况,其中这三人在同一个献血站献血的有2种结果,所以这三人在同一个献血站献血的概率为=.【点评】此题考查了树状图法求概率.注意树状图法适合两步或两步以上完成的事件,树状图法可以不重不漏的表示出所有等可能的结果,用到的知识点为:概率=所求情况数与总情况数之比.22.【分析】(1)设乙机器每天加工a个零件,根据甲、乙两台机器10天共生产(9200﹣5200)个零件列出方程,求出a得到乙机器每天加工250个零件;根据甲机器维修的时间即为乙机器单独工作的时间,结合图象根据工作时间=工作总量÷工作效率即可求出甲机器维修的天数;(2)分两种情况:①当10<x≤18时;②当18<x≤26时;利用待定系数法即可求解.【解答】解:(1)设乙机器每天加工a个零件,由题意得:10(150+a)=9200﹣5200,解得:a=250,即乙机器每天加工250个零件;甲机器维修的天数为=8(天).故答案为:250,8;(2)设未生产零件的个数y(个)与乙机器工作时间x(天)之间的函数关系式为y=kx+b.①当10<x≤18时,把(10,5200),(18,3200)代入,得:,解得:,∴y=﹣250x+7700(10<x≤18);②当18<x≤26时,把(18,3200),(26,0)代入,得:,解得:,∴y=﹣400x+10400(18<x≤26);综上所述,甲机器出现故障以后,未生产零件的个数y(个)与乙机器工作时间x(天)之间的函数关系式为:y=.【点评】本题考查了一元一次方程的应用,一次函数的应用,工作时间、工作总量与工作效率之间关系的应用,利用数形结合以及分类讨论是解题的关键.23.【分析】(1)作出以CD为直径的圆,利用直径所对的圆周角为直角可得该圆与AB的交点即为所求;(2)连接BD,利用等边三角形的判定与性质和全等三角形的判定与性质解答即可得出结论;(3)过点A作AF⊥BC于点F,过点E作EH⊥BC,延长HE交AD的延长线于点G,利用矩形的判定与性质,等腰直角三角形的判定与性质,全等三角形的判定与性质得到EH的长度,再利用等腰直角三角形的性质即可得出结论.【解答】解:(1)1.作出线段CD的垂直平分线,2.以CD为直径画圆,交AB于点E,3.连接DE,CE,则点E为所求.如图,(2)AD与CE之间的数量关系为:AD=CE,理由:连接BD,如图,∵BC=CD,∠C=60°,∴△BCD为等边三角形,∴BD=BC,∠CBD=∠CDB=60°,∵∠ABE=60°,∴∠ABE=∠CBD,∴∠ABD=∠EBC.∵AD∥BC,∴∠ADB=∠CBD=60°,∴∠ADB=∠C=60°.在△ABD和△EBC中,,∴△ABD≌△EBC(ASA),∴AD=EC;(3)过点A作AF⊥BC于点F,过点E作EH⊥BC,延长HE交AD的延长线于点G,如图,∵AD∥BC,AF⊥BC,EH⊥BC,∴四边形AFHG为矩形,∴AF=HG,∠G=∠FAG=90°.∵AB=AE,∠C=∠ABE=45°,∴∠ABE=∠AEB=∠C=45°,∴△ABE,△EHC为等腰直角三角形,∴∠BAE=90°,∠HEC=45°,∴∠GED=∠HEC=45°,∴△DEG为等腰直角三角形,∴DG=EG.∵∠BAE=∠FAG=90°,∴∠BAF=∠GAE.在△BAF和△EAG中,,∴△BAF≌△EAG(AAS),∴AF=AG,∴AG=GH,∴AG﹣DG=GH﹣GE,即:HE=AD=150(米),∴CE=EH=150(米).【点评】本题主要考查了尺规作图,梯形的性质,线段垂直平分线的判定与性质,圆的有关性质,圆周角定理,直角三角形的性质,等腰直角三角形的判定与性质,全等三角形的判定与性质,等边三角形的判定与性质,作出梯形的高线是解决此类问题常添加的辅助线.24.【分析】(1)将点P(﹣1,2)坐标代入y=kx+b即可得到b=k+2;(2)由(1)可知,直线y=kx+b=kx+k+2(k>0),可得A(﹣,0),B(0,k+2),根据面积公式和均值不等式求出S的取值范围即可;(3)先求出n与k的关系,然后用k表示出E,C的坐标,根据B和P的坐标关系,可以推出E和F 的坐标关系,从而得到F的坐标,代入抛物线解析式求得k值,即可求出C的坐标.【解答】解:(1)∵y=kx+b(k>0)经过点P(﹣1,2).∴﹣k+b=2,∴b=k+2(k>0).(2)由(1)可知,直线y=kx+b=kx+k+2(k>0),∴A(﹣,0),B(0,k+2),S==×(k+2)=×(4+k+),∵k>0,∴(﹣)2≥0,k﹣4+≥0,∴k+≥4,∴S=×(4+k+)≥×(4+4)=4,∴S的取值范围为:S≥4.(3)存在点F使四边形BPEF为平行四边形,理由如下:∵抛物线y=(x﹣k)2+n过点P(﹣1,2),∴2=(﹣1﹣k)2+n,∴n=﹣k2﹣2k+1,∴抛物线为y=(x﹣k)2﹣k2﹣2k+1(k>0),∴C(k,﹣k2﹣2k+1),当x=0,y=﹣2k+1,∴E(0,﹣2k+1),∵四边形BPEF为平行四边形,∴PB∥EF,PB=EF,∵点P向右平移1个单位长度、再向上平移k个单位长度得到点B,∴点E向右平移1个单位长度、再向上平移k个单位长度得到点F,∴F(0+1,﹣2k+1+k)即(1,﹣k+1),∵点F在抛物线上,∴(1﹣k)2﹣k2﹣2k+1=﹣k+1,解得:k=,∴C(,).【点评】本题主要考查了二次函数的性质,熟练掌握待定系数法求解一次和二次函数的解析式以及平行四边形的性质是本题解题的关键.25.【分析】(1)(Ⅰ)利用正方形的性质,勾股定理和直角三角形的边角关系定理解答即可;(Ⅱ)延长CB至点E,使BE=DM,连接AE,利用全等三角形的判定与性质得到EN=MN,设BN=m,DM=n,则MN=EN=m+n,利用直角三角形的边角关系定理得到CN=BC﹣BN=2m,CM=CD﹣DM=3m﹣n,利用勾股定理得到m,n的关系式3m=2n,从而CM=DM=n;(2)以AD为边作正方形ADEF,延长AN,交EF于点G,延长EF至点H,使FH=DM,连接AH,MG,延长CB交AF于点K,利用(1)(ii)的方法解答即可得出结论.【解答】(1)(Ⅰ)解:∵四边形ABCD是正方形,∴∠C=90°,∴CM===8,∴∠CMN的余弦值=;(Ⅱ)证明:延长CB至点E,使BE=DM,连接AE,如图,∵四边形ABCD是正方形,∴AB=AD,∠ABE=∠D=90°,在△ABE和△ADM中,,∴△ABE≌△ADM(SAS),∴EN=MN,设BN=m,DM=n,则MN=EN=m+n.∵tan∠BAN==,∴AB=3m,∴BC=CD=AB=3m,∴CN=BC﹣BN=2m,CM=CD﹣DM=3m﹣n.在Rt△CMN中,∵CN2+CM2=MN2,∴(2m)2+(3m﹣n)2=(m+n)2,∴3m=2n.∴CM=3m﹣n=2n﹣n=n,∵DM=n,∴CM=DM,∴M是CD的中点;(2)解:以AD为边作正方形ADEF,延长AN,交EF于点G,延长EF至点H,使FH=DM,连接AH,MG,延长CB交AF于点K,如图,∵四边形ADEF为正方形,∴AF=EF=DE=AD=16,∵四边形ABCD是直角梯形,AD∥BC,∠C=90°,∴四边形AKCD为矩形,∴CK=AD=16,AK=CD=12,∴KN=CK﹣CN=16﹣12=4,∵KN∥EF,∴△AKN∽△AFG,第15页(共15页)∴,∴,∴FG=.∴EG =EF ﹣FG =.在△AFH 和△ADM中,,∴△AFH ≌△ADM (SAS ),∴HG =MG .设DM =x ,则EM =16﹣x ,MG =HG =x ,∵EG 2+EM 2=MG 2,∴,解得:x =8.∴DM 的长为8.【点评】本题主要考查了正方形的性质,全等三角形的判定与性质,直角三角形的性质,勾股定理,直角三角形的边角关系定理,恰当的添加辅助线构造全等三角形是解题的关键。
广州一模理综试卷真正WORD版,图文清晰版含答案

普通高等学校招生全国统一考试广东省理科综合模拟试卷(一)本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,共14页,38小题,满分300分。
考试用时150 分钟。
注意事项:1.答题前,考生务必用0.5 毫米黑色字迹签字笔将自己所在的县(市、区)、学校以及自己的姓名、考生号、考场号和座位号填写在答题卡和试卷的指定位直,并用2B 铅笔在答题卡的“考生号”处填涂考生号。
2. 第I 卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在试卷、草稿纸和答题卡上的非答题区域均无效。
3. 第Ⅱ卷必须用0.5毫米黑色字迹签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置;女口需改动,先画掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带。
不按以上要求作答的答案无效。
4. 考试结束后,将本试卷和答题卡一并交回。
可能用到的相对原子质量: H 1 C 12 N 14 O 16 Mg 24 S 32 Cl 35.5 Fe 56 Co 59 Ag 108第I卷(选择题共126分)一、选择题:本题共13小题,每小题6分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.研究人员将猴胚胎细胞(a)中的细胞核取出,移植入一雌猴的去核卵母细胞(b)中,得到重组细胞(c),经培养获得胚胎并移植到另一雌猴(d)体内进一步发育,获得克隆猴(e)。
下列叙述正确的是A.e的细胞内的全部基因都来自a,b不提供基因B.c经一系列增殖和分化形成e的过程中,细胞核起控制作用C.d为胚胎发育提供遗传物质和其他适宜条件D.e的形成过程中没经过受精作用,其体细胞中无同源染色体2. 下列有关组织细胞中化合物鉴定实验的叙述,正确的是A.蛋白酶和蛋白质的混合溶液中加入双缩脲试剂后,会产生紫色反应B.将斐林试剂加入果糖溶液中后,溶液呈现无色,水浴加热后有砖红色沉淀生成C.观察DNA与RNA在细胞中分布的实验中,用盐酸处理有利于DNA与吡罗红结合D.酵母菌进行有氧呼吸和无氧呼吸的产物都能用酸性重铬酸钾溶液来鉴定3.炎性甲亢是由甲状腺滤泡细胞膜通透性发生改变,滤泡细胞中的甲状腺激素大量释放进入血液,而引起机体内甲状腺激素含量明显升高的一种疾病。
广东省广州市2024届高三下学期一模考试 物理 含答案

秘密*启用前试卷类型: A2024届广州市普通高中毕业班综合测试(一)物理本试卷共6页,15小题,满分100分。
考试用时75分钟。
注意事项:I.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名、考生号、试室号和座位号填写在答题卡上。
用2B铅笔将试卷类型(A)填涂在答题卡相应位置上,并在答题卡相应位置上填涂考生号。
2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案。
答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划悼原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效。
4.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
一、单项选择题:本题共7小题,每小题4分,共28分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1 某质点做简谐振动,其位移人与时间t的关系如图,则该压点A.振动频率为4Hzx/cmB.在A点时速度最大C.在B点时加速度最大tisD.在0~3s内通过路程为12.0cm2.我国自主研发的“华龙一号“反应堆技术利用铀235发生核裂变释放的能揽发电,典型的核反应方程为骂U+�n今婴Ba+��Kr+k护,光速取3.0X 108m/s ,若核反应的质量亏损为lg,释放的核能为t:,.E,则k和AE的值分别为A.2, 9.0X 10161C.2, 4.5XJ0咑B.3, 9.0X 10131D.3, 4.5X 10可3如图,一定质益的理想气体,用活塞封闭在开口向上的导热气缸内若环境温度不变,活塞与气缸壁间无庥掠,现对活塞施加向下压力使其缓慢下降,此过程中A.气体压强增大,内能增加B 气体压强增大,吸收热盘C 外界对气体做功,气体内能不变D.气体对外界做功,气体吸收热扭4.科学家研究发现,蜘蛛在没有风的情况下也能向上“起飞".如111,当地球表面带有负电荷,空气中有正电荷时,蜘蛛在其尾部吐出带电的蛛丝,在电场力的作用下实现向上“起飞“.下列说法正确的是A.蜘蛛往电势高处运动B 电场力对蛛丝做负功c.蛛丝的电势能增大D.蛛丝带的是正电荷5.无线充电技术已经在新能源汽车领域得到应用如图甲,与蓄电池相连的受电线圈置千地面供电线圆正上方,供电线圆输入如图乙的正弦式交变电流,下列说法正确的是20°l \/2/,(x l O飞)-20迈-----------------甲乙A.供电线圆中电流的有效值为2趴{iAB.受电线圆中的电流方向每秒钟改变50次C.t=O.O儿时受电线圈的感应电流最小D. t=O.Ols时两线圈之间的相互作用力最大6.某校天文小组通过望远镜观察木星周围的两颗卫星a 、b,记录了不同时刻t两卫星的位置变化如图甲.现以木星中心为原点,测量图甲中两卫星到木星中心的距离.x,以木星的左侧为正方向,绘出x-t图像如图乙已知两卫星绕木星近似做圆周运动,忽略在观测时间内观察者和木星的相对位置变化,由此可知卫星b卫星a木星.I. / 0时X.. . 2时--、. 4时\\'I/ /'Z飞左. . 6时右.8时.. 24时10.\、。
2024年广东省广州市白云区初三一模数学试题含答案解析

2024年广东省广州市白云区中考一模数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.2024-的相反数是( )A .2024-B .2024C .12024-D .12024【答案】B【分析】本题主要考查了求一个数的相反数,只有符号不同的两个数互为相反数,0的相反数是0,据此求解即可.【详解】解:2024-的相反数是2024,故选:B .2.一个几何体的三视图如图所示,则这个几何体是( )A .B .C .D .【答案】D【分析】根据主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形进行解答即可.【详解】解:根据主视图和左视图为矩形可判断出该几何体是柱体,根据俯视图是两个矩形可判断出该几何体为.故选:D .【点睛】本题考查由三视图想象立体图形.做这类题时要借助三种视图表示物体的特点,从主视图上弄清物体的上下和左右形状;从俯视图上弄清物体的左右和前后形状;从左视图上弄清楚物体的上下和前后形状,综合分析,合理猜想,结合生活经验描绘出草图后,再检验是否符合题意.3.下列运算正确的是( )A .()326m m =B .236m m m ⋅=C .22m m -=-D .222m m m ÷=4.某校举行“喜迎中国共产党建党105周年”党史知识竞赛,如图是10名决赛选手的成绩.对于这10名选手的成绩,下列说法中正确的是( )A .方差是0B .中位数是95C .众数是5D .平均数是905.不等式组23322322x x x -≥⎧⎪⎨+->⎪⎩的解集在数轴上表示为()A .B .C .D .3232x x ->--5x >-,∴不等式的解集为:51x -<≤-,故选:A .6.已知一次函数y ax b =+经过点()2,3--,正比例函数1y ax =不经过第三象限,则反比例函数2b y x=的图象位于( )A .第一、第二象限B .第一、第三象限C .第二、第三象限D .第二、第四象限7.端午节,赛龙舟,小亮在点P 处观看400米直道竞速赛,如图所示,赛道AB 为东西方向,赛道起点A 位于点P 的北偏西30︒方向上,终点B 位于点P 的北偏东60︒方向上,400AB =米,则点P 到赛道AB 的距离为( )米.A .B .C .87D .173 3ta n303AC PC x ∴=⋅︒=60CPB ∠=︒ta n603BC PC x∴=⋅︒=AB 8.某校组织540名学生去外地参观,现有A ,B 两种不同型号的客车可供选择.在每辆车刚好满座的前提下,每辆B 型客车比每辆A 型客车多坐15人,单独选择B 型客车比单独选择A 型客车少租6辆.设A 型客车每辆坐x 人,根据题意可列方程( )A .54015x -﹣540x =6B .540x ﹣54015x +=6C .54015x +﹣540x =6D .540x ﹣54015x -=6列出相应的方程.9.如图,ABC 的内切圆I 与BC ,CA ,AB 分别相切于点D ,E ,F ,若I 的半径为r ,FDE α∠=,则()AF CD AC +-的值和A ∠的大小分别为( )A .0,1802α︒-B .r ,180α︒-C ,90α︒-D ,902α︒-【答案】A 【分析】本题考查三角形的内切圆,圆周角定理,切线长定理等知识.连接,IF IE .利用切线长定理,可得,,,AF AE CD CE IF AB IE AC =⊥⊥=,从而得到AF CD AC +-,再由圆周角定理,可得22EIF EDF α∠=∠=,即可.【详解】解:如图,连接,IF IE .∵ABC 的内切圆I 与BC ,CA ,AB 分别相切于点D ,E ,F ,∴,,,AF AE CD CE IF AB IE AC =⊥⊥=,∴090,C A C F CD A AE CE AC A A AFI AEI C =+︒+--=-=∠=∠=,∴22EIF EDF α∠=∠=,∴3601802A AFI AEI EIF α∠=︒-∠-∠-∠=︒-.故选:A1021-=-,则关于x 的方程()222210x k x k --+-=根的情况是( )A .无实数根B .有两个相等的实数根C .有两个实数根D .有两个不相等的实数根【答案】C 【分析】本题考查了算术平方根的非负性,一元二次方程根的判别式.熟练掌握算术平方根的非二、填空题11.2023年10月26日上午,神州十七号载人飞船载着杨洪波、唐胜杰、江新林3名航天员奔赴“天宫”,从2003年的神舟五号到2023年的神州十七号,20年中国载人航天工程共有20位航天员问鼎苍穹,截止到目前为止,我国航天员在太空的时间已累计达到近21200个小时,其中,数字21200用科学记数法表为.12.若点()11A y -,,212B y ⎛⎫ ⎪⎝⎭,,()32C y ,在抛物线()22y x k =-+上,则1y ,2y ,3y 的大小关系为 (用“>”连接)13.2023年5月30日是第7个全国科技工作者日,某中学举行了科普知识手抄报评比活动,共有100件作品获得一、二、三等奖和优胜奖,根据获奖结果绘制如图所示的折线图,若将获奖作品按四个等级所占比例绘制成扇形统计图,则“二等奖”对应扇形的圆心角度数为 .14.如图,正方形ABCD 的边长为4,点E 在边BC 上,F 为对角线BD 上一动点,连接CF ,EF ,若CF EF +的最小值CE = .∵正方形ABCD ,∴4AB BC ==∠,又∵BF BF =,15.如图,已知AD 是ABC 的角平分线,DE ,DF 分别是ABD △和ACD 的高,四边形AEDF 的面积为60,5DF =,则ADE V 中AD 边上的高为 .16.如图,矩形ABCD 中,9AB =,12AD =,点P 从A 出发以每秒3个单位长度的速度沿A D C B A →→→→运动一周到点A 停止.当点P 不与矩形ABCD 的顶点重合时,过点P 作直线PQ BC ⊥,与矩形的边的另一交点为Q .若点P 的运动时间为t ,当810t <<时,CQ 长度的范围是.PC=-∴12421由勾股定理得t=时,点当10三、解答题17.解方程:x 2+4x ﹣12=0.【答案】x 1=﹣6,x 2=2【分析】利用因式分解法解一元二次方程即可.【详解】解:原方程变形为:(x +6)(x ,﹣2)=0,∴x +6=0或x ﹣2=0,∴x 1=﹣6,x 2=2.【点睛】本题考查解一元二次方程,熟练掌握一元二次方程的解法并能灵活运用是解答的关键.18.已知:如图,在Rt ABC △中,90ACB ∠=︒,过点C 作CD AB ⊥,垂足为D .在射线CD 上截取CE CA =,过点E 作EF CE ⊥,交CB 的延长线于点F .求证:BC FE =.【答案】见详解【分析】本题考查全等三角形的判定.根据题意,先得出E ACB ∠=∠,再用两角夹边判定即可.【详解】证明: CD AB⊥90A ACD ∴∠+∠=︒90ACB ∠=︒90ACD ECF ∴∠+∠=︒A ECF∴∠=∠ EF CE⊥90E ∴∠=︒E ACB∴∠=∠在ACB △和CEF △中A ECF CE CAE ACB ∠=∠⎧⎪=⎨⎪∠=∠⎩(AS A)ACB CEF ∴ ≌BC FE ∴=.19.如图,在平面直角坐标系xOy 中,点()2,0A -, AB 所在圆的圆心为O ,60AOB ∠=︒,将 AB向右平移5个单位,得到 CD (点A 平移后的对应点为C ).(1)点B 的坐标是___________, AB 所在圆的圆心坐标是___________.(2)在图中画出 CD,求 CD 的长.2OA OB ∴==1cos60212OE OB ∴=⋅︒=⨯=,BE由平移的性质知60CGD ∠=︒且GC OA =∴ CD 的长为602223603ππ⨯⨯=.20.给出6个整式:2x +,2x -,21x +,2,21x x +-,211--x x .(1)从上面的6个整式中选择2个合适的整式,组成一个分式;(2)从上面的6个整式中选择2个合适的整式进行乘法运算,使运算结果为一个不含有一次项的多项式,请你列出算式,并写出运算过程.21.甲、乙、丙三人各自随机选择到A,B两个献血站进行爱心献血.求这三人在同一个献血站献血的概率.22.某车间甲、乙两台机器共生产9200个零件,两台机器同时加工一段时间后,甲机器出现故障,维修一段时间后仍按原来的效率加工,已知甲机器每天加工150个零件,如图是表示未生产零件的个数y(个)与乙机器工作时间x(天)之间的函数图象.(1)乙机器每天加工__________个零件,甲机器维修了__________天;(2)求甲机器出现故障以后,未生产零件的个数y(个)乙机器工作时间x(天)之间的函数关系式.【答案】(1)250;8(2)()()25077001018400104001826x x y x x ⎧-+<≤⎪=⎨-+<≤⎪⎩【分析】本题主要考查了一次函数的实际应用:(1)设乙机器每天加工a 个零件,甲机器每天加工150个零件,根据前10天是两个机器一起工作,结合数量关系列方程求解即可;再由AB 段是乙单独工作,求出乙单独工作的时间即可求出甲维修的时间;(2)根据函数图像函数关系式为()0y kx b k =+≠,当1018x <≤时,图像过点()10,5200,()18,3200;当1826x <≤时,图像过点()18,3200,()26,0,运用待定系数法即可求解.【详解】(1)解:设乙机器每天加工a 个零件,由题意得,()1015092005200a +=-,解得,250a =,根据题意,从点A 到点B 是乙单独完成的量,∴520032002000-=(个),∴20002508÷=(天),∴甲维修了8天,故答案为:250;8.(2)解:设未生产零件的个数y (个)与乙机器工作时间x (天)之间的函数关系式为()0y kx b k =+≠,由(1)可知,甲维修了8天,则点B 的坐标为()18,3200,∴当1018x <≤时,图像过点()10,5200,()18,3200,∴105200183200k b k b +=⎧⎨+=⎩,解得2507700k b =-⎧⎨=⎩,∴2507700y x =-+;③当1826x <≤时,图像过点()18,3200,()26,0,∴183200260k b k b +=⎧⎨+=⎩,解得40010400k b =-⎧⎨=⎩,∴40010400y x =-+;综上所述,未生产零件的个数y (个)与乙机器工作时间x (天)之间的函数关系式为()()25077001018400104001826x x y x x ⎧-+<≤⎪=⎨-+<≤⎪⎩.23.【问题探究】(1)如图①,在四边形ABCD 中,90A B ∠=∠=︒,在AB 边上作点E 为一点,连接CE ,DE ,使得CE DE ⊥(画出一个点E 即可,要求用尺规作图,保留作图痕迹,不要求写作图的证明);(2)如图②,在四边形ABCD 中,AD BC ∥,BC CD =,60C ∠=︒,点E 为CD 上一点,连接AE ,BE ,60ABE ∠=︒,试判断AD 与CE 之间的数量关系,并说明理由;【问题解决】(3)如图③,四边形ABCD 是赵叔叔家的果园平面示意图,点E 为果园的一个出入口(点E 在边CD 上),AE ,BE 为果园内的两条运输通道(通道宽度忽略不计),经测量,AD BC ∥,AB AE =,45C ABE ∠=∠=︒,150AD =米,赵叔叔计划在BCE 区域内种植某种果树,并沿CE 修建一条安全栅栏,为提前做好修建安全栅栏的预算,请你帮赵叔叔计算出CE 的长度.理由:由作法得:OC OD OE ==,∴,ODE OED OCE OEC ∠=∠∠=∠,∴ODE OCE OED OEC DEC ∠+∠=∠+∠=∠,∵180ODE OCE DEC ∠+∠+∠=︒,∴90DEC ∠=︒,∴DE CE ⊥;(2)AD CE =,理由如下:如图,连接BD ,∵BC CD =,60C ∠=︒,∴BCD △是等边三角形,∴BC BD =,60CBD ∠=︒,∵60ABE ∠=︒,∴60ABE CBD ∠=∠=︒,∴ABD CBE ∠=∠,∵AD BC ∥,∴60ADB CBD C ∠=∠=︒=∠,在ABD △和EBC 中,∵ABD CBE ∠=∠,BC BD =,ADB C ∠=∠,∴()ASA ABD EBC ≌,∵AD BC ∥,45C ∠=︒,∴45ADF C ∠=∠=︒,∴ADF △是等腰直角三角形,∴150AF AD ==米,∵AB AE =,∴45AEB ABE ∠=∠=︒,24.已知直线():0l y kx b k =+>经过点()1,2P -.(1)用含有k 的式子表示b ;(2)若直线l 与x ,y 轴分别交于A ,B 两点,AOB 面积为S ,求S 的取值范围;(3)过点P 的抛物线()2y x k n =-+与y 轴交点为E ,记抛物线的顶点为C ,该抛物线是否存在点F 使四边形BPEF 为平行四边形?若存在,求此时顶点C 的坐标;若不存在,请说明理由.【答案】(1)2b k =+25.如图,在四边形ABCD 中,点N ,M 分别在边BC ,CD 上.连接AM ,AN ,MN ,45MAN ∠=︒.(1)【实践探究】如图①,四边形ABCD 是正方形.(ⅰ)若6CN =,10MN =,求CMN ∠的余弦值;(ⅱ)若1an 3t BAN =∠,求证:M 是CD 的中点;(2)【拓展】如图②,四边形ABCD 是直角梯形,AD BC ∥,90C ∠=︒,12CD =,16AD =,12CN =,求DM 的长.∵四边形ABCD是正方形,AB CD AD BAD,∴==∠=∠由旋转的性质得:ABE≌BE DM ABE D,90∴=∠=∠=∵90C ∠=︒,12CD =,16AD =,CN ∴16,12====AD CE AE CD ,∴4==-=EP EN CE CN ,∴16=+==AP AE EP AD ,∴四边形APGD 是正方形,。
2024年广东省广州市部分学校中考一模语文试题(含答案)
秘密★启用前2024年广州市初中学业水平考试语文考生号:_______________________ 姓名:_______________________ 本试卷共8页,20小题,另设有附加题。
满分120分。
考试用时120分钟。
注意事项:1. 答题前,考生务必在答题卡第1面和第3面用黑色字迹的钢笔或签字笔填写自己的考生号、姓名;将自己的条形码粘贴在答题卡的“条形码粘贴处”。
2. 选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。
答案不能答在试卷上。
3. 非选择题答案必须用黑色字迹的钢笔或签字笔写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案,改动后的答案也不能超出指定的区域;不准使用铅笔、涂改液和修正带。
不按以上要求作答的答案无效。
4. 本试卷设有附加题,共8分,考生可答可不答;该题得分作为补偿分计入总分,但全卷最后得分不得超过120分。
5. 考生必须保持答题卡的整洁,考试结束后,将本试卷和答题卡一并交回。
第一部分积累与运用(共24分)一、(5小题,16分)1. 下列词语中,每对加点字的读音都相同的一项是(2分)A. 缄.默/箴.言佝偻./伛偻.提携B. 镌.刻/隽.永绯.红/妄自菲.薄C. 杳.然/拖沓.粗犷./心旷.神怡D. 伫.立/贮.蓄隐晦./诲.人不倦2. 下列词语中,没有..错别字的一项是(2分)A. 秀颀吹毛求疵遏制名副其实B. 决别春寒料峭雾霭责无旁待C. 寒喧谈笑风声娴熟诚惶诚恐D. 分歧不屑置辨缈茫慷慨淋漓3.下列句子中,加点词语使用最恰当的一项是(2分)A. 莫高窟是无数大师前仆后继....,用智慧和汗水建造出来的一座瑰丽的艺术宫殿。
B.多少年来,几代执着的中国人殚精竭虑....地为中华民族的伟大复兴而努力奋斗。
C. 司马迁研读各家史著,搜罗天下遗闻轶事,断章取义....,终著成《史记》一书。
2024广州一模历史试题+参考答案(word版)
2024广州一模历史试题+参考答案(word版)2024届广东省广州市高三一模考试历史试题一、选择题:本题共16小题,每小题3分,共48分。
在每小题给出的四个选项中,只有一项符合题目要求。
1.考古发现,二里头陶质酒礼器中的鬶、盉与爵都是以大汶口——山东龙山文化的鬶为原型创造出来的,玉璋等礼器也源自山东龙山文化。
这些二里头文化的陶盉、爵等礼器,后来在长江流域、黄河上游等地皆有发现,玉璋也见于四川盆地、红河三角洲等地。
这可说明A.南北经济存在差异B.中华文明由多元走向一体C.阶级分化日益明显D.二里头周边贸易网络发达2.据载,郑弘少为乡夫,被太守第五伦举为孝廉。
元和元年(84年)郑弘为太尉,第五伦为司空,班次在郑弘之下。
“每正朔朝见,郑弘曲躬而自卑。
帝问其故,遂听置云母屏风,分隔其间。
由此以为故事(定例)。
”这反映了A.豪强势力的膨胀B.君主专制日益加强C.察举制存在隐忧司D.官僚体制逐步健全3.公元3世纪,鲜卑开启了姓氏和婚制改革,将族众分为十个族氏,规定十氏百世不通婚。
此后,鲜卑十氏与外姓族广泛通婚。
这一改革A.推动了鲜卑步入早期国家阶段B.保证了氏族贵族的政治优势C.旨在打乱原有的民族部落布局D.构建了长幼有序的伦理秩序4.唐代初期,政务事项原则上都要先向尚书省申报,再以尚书省的名义奏报皇帝。
唐高宗和武则天之后,却逐渐形成了“事无大小,皆悉闻奏”的局面,比如有太学生直接向武则天告假回家,还得到了武则天应允。
这一变化可以说明A.监察制度日趋完善B.官僚机构对皇权的限制愈加艰难C.行政效率不断降低D.中央政府对地方的控制逐步加强5.宋代,政府明确了土地交易的程序,在典卖田宅议定价钱之后的三日内,经官纳“定帖钱”(定贴,即产权证明),然后纳税买“钞旁”(纳税凭证)。
这有助于A.抑制大土地所有制发展B.增加政府的财政收入C.加强对农民的人身控制D.推动南北经济的交流6.明初,广西思恩府土司岑瑛因“筑城池,创廊宇,立学校,建祠庙,政绩大著”,被明政府升任“都指挥同知”,给予流官职位。
2024年广东省广州市荔湾区中考一模语文试题(解析版)
2024届初中毕业班学业水平综合测试(荔湾)九年级语文第一部分积累与运用(共24分)一、(5小题,16分)1. 下列词语中,每对加点字的读音都相同的一项是()A. 箴言/缄默妥当/锐不可当B. 折损/折腰瞭望/眼花缭乱C. 贮蓄/伫立咀嚼/味同嚼蜡D. 执着/着意取缔/根深蒂固【答案】D【解析】【详解】本题考查字音。
A zhēn/jiān,dàng/dāng;.B.zhé/zhé,liào/liáo;C.zhù/zhù,jué/jiáo;D.zhuó/zhuó,dì/dì;故选B。
2. 下列词语中,没有错别字的一项是()A. 弥漫振聋发聩凌乱人情事故B. 侦缉格物至知涉猎自圆其说C. 深宵坦荡如坻枯燥名副其实D. 轻捷言不及义诀别轻歌曼舞【答案】D【解析】【详解】本题考查字形。
A.人情事故——人情世故;B.格物至知——格物致知;C.坦荡如坻——坦荡如砥;故选D。
3. 下列句子中,加点词语使用最恰当的一项是()A. 今年春季入伍的38名女兵,在亲戚朋友们前呼后拥地喑伴下走进军营。
B. 小清作为“梦想”号科考船研究员,每天工作千头万绪,如群蚁排衙。
C. 受到冷空气及大风影响。
部分地区将出现令人叹为观止的特强沙尘暴。
D. 桑寄生以咄咄逼人的气势缠绕在树冠上,遮挡了木棉赖以生长的日光【答案】D【解析】【详解】本题考查词语的运用。
A.前呼后拥:前面有人吆喝开路,后面有人围着保护。
旧时形容官员出行,随从的人很多。
句中用于形容亲戚朋友们陪伴新入伍的女兵,使用对象错误,不符合语境,使用不恰当;B.群蚁排衙:指许许多多的蚂蚁排列成行,也指事物或者队伍整齐地排列着。
句中用于形容每天的工作很多,不符合语境,使用不恰当;C.叹为观止:指赞美所看到的事物好到极点,无与伦比。
句中用于形容特强沙尘暴,使用对象错误,不符合语境,使用不恰当;D.咄咄逼人:形容气势光泽,盛气凌人,使人难堪;也指形势发展迅速,给人压力。
2024年广东省广州市中考一模语文试卷(含答案)
2023-2024学年广州第二学期九年级综合训练语文本综合训练卷分选择题和非选择题两部分,共五大题20小题,另外设有附加题。
共8页,满分120分。
用时120分钟。
注意事项:1.答卷前,考生务必在答题卡上用黑色字迹的钢笔或签字笔填写自己的考生号、姓名;同时填写考点考场号、座位号,再用2B铅笔把对应这两个号码的标号涂黑。
2.选择题的答案用2B铅笔把答题卡上选择题答题区中对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案;答案不能写在试卷上。
3.非选择题答案必须用黑色字迹的钢笔或签字笔写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案,改动后的答案也不能超出指定的区域:不准使用铅笔、圆珠笔和涂改液,不按以上要求作答的答案无效。
4.学生必须保持答题卡的整洁,考试结束后,将本问卷和答题卡一并交回。
第一部分 积累与运用(共24分)一、(本大题共5小题,满分16分)1.下列词语中,每对加点字的读音都相同的一项是( )(2分)A.蜗.行/笑涡.均.匀/千钧.之力B.旗帜./炽.热 扭绞./月光皎.洁C.恐吓./惊吓. 累.赘/伤痕累.累D.侍.候 伺.机威胁./两肋.插刀2.下列词语中,没有错别字的一项是( )(2分)A.顷刻 血雨腥风瘦峭不屑置辨B.侦缉 胸有成竹婉惜 无精打彩C.囫囵 身临其境契合雕梁画栋D.要决 望眼欲穿驾驭意想天开3.下列句子中,加点词语使用恰当的一项是( )(2分)A.他认真听讲、努力学习、认真完成作业,终于取义成仁....,在考试获得了理想成绩。
B.同学们毕业后再回母校,最喜欢和班主任小王老师坐在操场聊天,享受天伦之乐....。
C.虽然这个玩具摔碎了,但他妙手回春....,一会儿工夫就把摔碎的玩具修得完好如初。
D.生活中,那些善于观察、勤于思考的人大都文思敏捷,写起文章来总是一气呵成....。
4.下列句子中,没有语病的一项是( )(2分)A.“奋斗者”号四年达成了多次下潜任务,其中深度超过一万米的达25次。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013年广州市普通高中毕业班综合测试(一)
地理试题
2013. 3
一、选择题:本题包括35小题,每小题4分,共140分。
每小题给出的四个选项中,只有一个选项符合题目要求。
南极磁点大约位于139°24′E、65°36′S,完成1~2题。
1.南极点与南极磁点相距约
A.0千米B.2800千米C.3500千米D.4500千米
2.在南极地区,判断地理方位最好利用
A.指南针B.北极星C.太阳D.GPS
读“2000~2007年开都河径流变化图”,完成3~5题。
3.开都河最主要的补给类型是
A.冰川B.雨水C.地下水D.湖泊水
4.开都河下游地区自然带最可能是
A.温带森林带B.温带森林、草原带C.高山草甸带D.温带荒漠带
5.开都河下游地区的外力作用最主要是
A.流水作用B.冰川作用C.风力作用D.波浪作用
读“北京市人口密度和就业密度变化图”,完成6~7题。
6.近20年北京市人口迁移的特点是
A.从远郊、近郊向市中心迁移B.从城市中心向近郊、远郊迁移
C.从城市中心、远郊向近郊迁移D.从远郊向近郊、城市中心迁移
7.从北京市人口密度和就业密度变化状况来看,其城市化存在
A.城市经济发展缓慢,就业压力大
B.城市规模不断扩大,大量企业迁往远郊,造成上下班交通堵塞
C.传统工业发展迅猛,人均绿地面积不断减少
D.人口密度与就业密度的变化不一致,造成上下班交通严重拥挤
2008年我国太阳能电池生产量,占全球总量的26%,成为继日本和欧盟之后的第三大生产国。
但与此形成鲜明对比的是,2008年我国光伏系统安装量,仅占全球总安装量的0.73%。
下表是我国光伏企业空间分布统计图表,完成8~9题。
8.影响我国光伏企业分布的最主要区位因素是
A.太阳辐射B.世界市场C.自然资源D.国家政策
9.我国太阳能(光伏)发电最具发展潜力的地区在
A.长江三角洲B.珠江三角洲C.西北地区D.东北地区
读“2007年我国各省区人均碳足迹(即人均碳排放量,单位:吨/人年)示意图”,完成10~11题。
10.我国人均碳足迹分布特点是
A.北多,南少B.西南多,东北少C.东多,西少D.沿海多,内地少
11.影响我国人均碳足迹分布的最主要区位因素是
A.经济水平B.产业结构C.技术水平D.交通运输
40.(28分)2013年2月18日巴基斯坦瓜达尔港运营权由新加坡企业移交给中国企业。
根据下列材料,结合所学知识,完成(1)~(5)题。
材料一:瓜达尔港区位及其周边地区示意图。
材料二:瓜达尔港建成投入使用后,一直由新加坡国际港务集团负责管理经营。
其官方网站上公开
的信息显示,从2012年11月以来,没有一艘商船光顾瓜达尔港。
在过去7年的绝大部分时间里,瓜达尔
港基本上都处于闲置状态。
(1)瓜达尔港地处__________(海湾)通往__________(洋)的石油运输最重要的航线上,扼守进出__________海峡的咽喉。
(6分)
(2)我国计划建设连接喀什与瓜达尔港的铁路和高速公路,使之成为我国西部地区通往南亚、______亚的重要通道,这将大大缩短我国输人__________战略资源的路径。
(4分)
(3)恒河流域最主要的气候类型是__________;瓜达尔气候特征是__________。
(4分)
(4)试分析图中三大河流流域成为人类文明发源地的优越地理条件。
(6分)
(5)瓜达尔深水港一直处于闲置状态,综合分析其区位原因。
(8分)
41.(28分)我国北方地区沙漠化土地面积较20世纪末有所减少,沙漠化整体扩展的趋势已得到初步抑制。
根据下列材料,结合所学知识,完成(1) ~ (4)题。
材料一:陕西省榆林地区区位示意图。
材料二:1990~2010年榆林地区人类活动强度变化示意图。
(1)榆林地区地处我国__________高原和__________高原的交界,处于__________气候向__________气候的过渡地带。
(8分)
(2)榆林地区北部主要受________(外力)作用的影响,而南部主要受__________的侵蚀作用。
(4分)(3)试分析1998年以前榆林地区的人地关系矛盾及其出现的生态环境问题。
(8分)
(4)1998年以来,榆林地区生态环境得到了较好的综合整治,试指出其治理的措施。
(8分)2013年广州市普通高中毕业班综合测试(一)
文科综合·地理试题参考答案及评分标准
40.(28分)
(1)①波斯湾(阿曼湾)②印度洋③霍尔木兹(每空2分,共6分)
(2)①西亚(中东)②石油(每空2分,共4分)
(3)①热带季风气候②终年高温、干旱(每空2分,共4分)
(4)①地处热带,光热充足;②河流,水源资源充足;③平原,地势低平;④土层深层,土壤肥沃,发展农业生产的条件优越。
(每点2分,共6分,若答案合理,可酌情给分,但不能超过本小题
总分)
(5)①地处西南边境,远离印度河平原;②交通落后,缺少铁路、公路与其他地区联系;③腹地为荒漠地区,人口、城市较少;④本地区工农业生产较落后,缺少货物运输。
(每点2分,共8分,若答案合理,可酌情给分,但不能超过本小题总分)
41.(28分)
(1)①内蒙古②黄土高原③温带大陆性④温带季风(每空2分,共8分)
(2)①风力②流水(每空2分,共4分)
(3)①人口和非农业人口数量不断增长,粮食等压力不断增大;②毁林开荒;③开垦草原,过渡放;
④本地区地处气候过渡地带,生态环境脆弱;⑤人地关系紧张,人口——粮食等——环境呈现
恶性循环。
引起①北部荒漠化和②南部严重水土流失生态环境环境问题(每点2分,共8分;
若答案合理,可酌情给分,但不能超过本小题总分)
(4)①退耕还林、退耕还牧;②植树造林、种草;③改变农业生产方式和结构;④建设三北防护林和南部水土保持林;⑤开展开部治沙、南部打坝淤地等保持水土项目。
(每点2分,共8分;若
答案合理,可酌情给分,但不能超过本小题总分)。
