14-7 圆孔衍射 光学仪器的分辨率
合集下载
11.3 圆孔衍射 光学仪器的分辨本领
一般光学仪器成像，可以看成圆孔衍射。由于衍射现象， 一般光学仪器成像，可以看成圆孔衍射。由于衍射现象， 会使图像边缘变得模糊不清，使图像分辨率下降。 会使图像边缘变得模糊不清，使图像分辨率下降。
(1) 瑞利准则 瑞利准则:
两个点光源相距较远，能分辨。 两个点光源相距较远，能分辨。 两个点光源相距较远
能分辨
S1
S2
恰能分辨
S1
S2
不能分辨
S1
S2
(2) 光学仪器分辨率
两光点刚好能分辨时, 我们把两物点在透镜处的张角称为最 两光点刚好能分辨时 我们把两物点在透镜处的张角称为最 小分辨角， δθ表示 可知： 表示， 小分辨角，用δθ表示，可知：
δθ = 1.22
1
λ
d
最小分辨角的倒数称为光学仪器的分辨率
d R= = δθ 1.22λ
光学仪器的最小分辨角越小，分辨率就越高。 光学仪器的最小分辨角越小，分辨率就越高。
光学镜头直径越大，分辨率越高。 光学镜头直径越大，分辨率越高。 光学镜头直径越大 采用波长较短的光，也可提高分辨率。 采用波长较短的光， 采用波长较短的光 也可提高分辨率。
一般天文望远镜的口径都很大， 一般天文望远镜的口径都很大，世界上最大的天 文望远镜在智利，直径16米，由4片透镜组成。 文望远镜在智利，直径 米 片透镜组成。 片透镜组成 美国最大的望远镜直径为200英寸，在帕洛玛山。 英寸，在帕洛玛山。 美国最大的望远镜直径为 英寸
地面观测
用哈勃望远镜 观测
d R= = δθ 1.22λ
采用波长较短的光，也可提高分辨率。 采用波长较短的光，也可提高分辨率。 采用波长较短的光 电子显微镜用加 速的电子束代替光束， 速的电子束代替光束 ， 其波长约 0.1nm， 用 ， 它来观察分子结构。 它来观察分子结构。
(1) 瑞利准则 瑞利准则:
两个点光源相距较远，能分辨。 两个点光源相距较远，能分辨。 两个点光源相距较远
能分辨
S1
S2
恰能分辨
S1
S2
不能分辨
S1
S2
(2) 光学仪器分辨率
两光点刚好能分辨时, 我们把两物点在透镜处的张角称为最 两光点刚好能分辨时 我们把两物点在透镜处的张角称为最 小分辨角， δθ表示 可知： 表示， 小分辨角，用δθ表示，可知：
δθ = 1.22
1
λ
d
最小分辨角的倒数称为光学仪器的分辨率
d R= = δθ 1.22λ
光学仪器的最小分辨角越小，分辨率就越高。 光学仪器的最小分辨角越小，分辨率就越高。
光学镜头直径越大，分辨率越高。 光学镜头直径越大，分辨率越高。 光学镜头直径越大 采用波长较短的光，也可提高分辨率。 采用波长较短的光， 采用波长较短的光 也可提高分辨率。
一般天文望远镜的口径都很大， 一般天文望远镜的口径都很大，世界上最大的天 文望远镜在智利，直径16米，由4片透镜组成。 文望远镜在智利，直径 米 片透镜组成。 片透镜组成 美国最大的望远镜直径为200英寸，在帕洛玛山。 英寸，在帕洛玛山。 美国最大的望远镜直径为 英寸
地面观测
用哈勃望远镜 观测
d R= = δθ 1.22λ
采用波长较短的光，也可提高分辨率。 采用波长较短的光，也可提高分辨率。 采用波长较短的光 电子显微镜用加 速的电子束代替光束， 速的电子束代替光束 ， 其波长约 0.1nm， 用 ， 它来观察分子结构。 它来观察分子结构。
10-08 圆孔衍射 光学仪器分辨率最新版物理学精品课件完美版
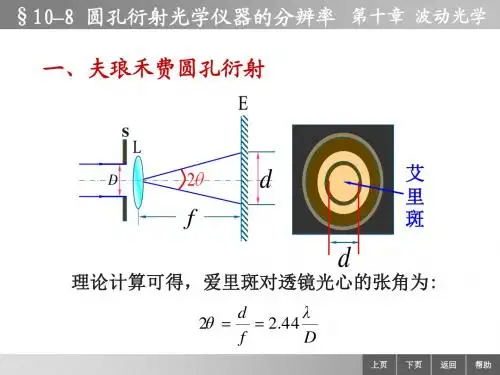
§10–8 圆孔衍射光学仪器的分辨率 第十章 波动光学一、夫琅禾费圆孔衍射EsDL
2
d
f
艾 里 斑
理论计算可得，爱里斑对透镜光心的张角为:
d λ 2θ 2.44 f D
上页 下页 返回 帮助
d
§10–8 圆孔衍射光学仪器的分辨率 第十章 波动光学
二、光学仪器的分辨率（两光点刚好能分辨）
s1 * s 2*
d0 d
2
f
1.22 D
1
d0 d f 2f
最小分辨角
光学仪器分辨率
1 D D, 1.22
上页 下页 返回 帮助
§10–8 圆孔衍射光学仪器的分辨率 第十章 波动光学
1990 年发射的哈勃 太空望远镜的凹面物镜 的直径为2.4m ，最小分 辨角 0.1" ，在大气层 外 615km 高空绕地运行, 可观察130亿光年远的太 空深处, 发现了500 亿个 星系。
上页 下页 返回 帮助
§10–8 圆孔衍射光学仪器的分辨率 第十章 波动光学
例10-2 人眼的瞳孔直径为23mm，在明亮的环境中， 感觉最敏感的是黄绿光，波长为550nm，人眼中玻璃液的折 射率为 n 1.336 。试求： （1）人眼的最小分辨角； （2）若物体放在距人眼25cm（明视距离）处，则两物 点间距为多大时才能被分辨？ 解：（1）设人眼瞳孔的直径取 在玻璃液中光波波长
设两物点的距离为 y （ 2） 人眼的明视距离为l,则人眼的最小分辨角
y
l
y l 0.25 2.5 104 m=6.310－5m
所以两物点相距大于6.3 10 m时，才能被人眼所分辨。
5
上页 下页 返回 帮助
2
d
f
艾 里 斑
理论计算可得，爱里斑对透镜光心的张角为:
d λ 2θ 2.44 f D
上页 下页 返回 帮助
d
§10–8 圆孔衍射光学仪器的分辨率 第十章 波动光学
二、光学仪器的分辨率（两光点刚好能分辨）
s1 * s 2*
d0 d
2
f
1.22 D
1
d0 d f 2f
最小分辨角
光学仪器分辨率
1 D D, 1.22
上页 下页 返回 帮助
§10–8 圆孔衍射光学仪器的分辨率 第十章 波动光学
1990 年发射的哈勃 太空望远镜的凹面物镜 的直径为2.4m ，最小分 辨角 0.1" ，在大气层 外 615km 高空绕地运行, 可观察130亿光年远的太 空深处, 发现了500 亿个 星系。
上页 下页 返回 帮助
§10–8 圆孔衍射光学仪器的分辨率 第十章 波动光学
例10-2 人眼的瞳孔直径为23mm，在明亮的环境中， 感觉最敏感的是黄绿光，波长为550nm，人眼中玻璃液的折 射率为 n 1.336 。试求： （1）人眼的最小分辨角； （2）若物体放在距人眼25cm（明视距离）处，则两物 点间距为多大时才能被分辨？ 解：（1）设人眼瞳孔的直径取 在玻璃液中光波波长
设两物点的距离为 y （ 2） 人眼的明视距离为l,则人眼的最小分辨角
y
l
y l 0.25 2.5 104 m=6.310－5m
所以两物点相距大于6.3 10 m时，才能被人眼所分辨。
5
上页 下页 返回 帮助
圆孔衍射
6
S1 S2
可分辨 此时两爱 里斑重叠 部分的光 强为一个 光斑中心 最大值的 80％。 ％。
S1 S2
恰可分辨
两爱里斑中心距d 恰好等于爱里斑半径。 两爱里斑中心距 0恰好等于爱里斑半径。
S1 S2
不可分辨
7
2.光学仪器分辨率 光学仪器分辨率 满足瑞利判据的两物点间的距离， 满足瑞利判据的两物点间的距离，就是光学仪器 所能分辨的最小距离。 所能分辨的最小距离。此时两个物点对透镜中心所张 的角δϕ称为最小分辨角。 δϕ称为最小分辨角 的角δϕ称为最小分辨角。 d0为光学仪器可分辨的最小距离，即为两物点可 为光学仪器可分辨的最小距离， 分辨的最小距离， 为圆孔到两物点的垂直距离， 分辨的最小距离，L为圆孔到两物点的垂直距离，若为 光学仪器， 即为焦距f 为圆孔直径。 光学仪器，则L即为焦距f。D为圆孔直径。 光学仪器中将最小分辨角的倒数称为仪器的分辨率 光学仪器中将最小分辨角的倒数称为仪器的分辨率。
4
二、光学仪器的分辨本领
一般光学仪器成像， 一般光学仪器成像，光学仪器对点物成象是一个 有一定大小的爱里斑。 有一定大小的爱里斑。 所以由于衍射现象 会使图像边缘变得模糊不清， 由于衍射现象， 所以由于衍射现象，会使图像边缘变得模糊不清， 使图像分辨率下降。 使图像分辨率下降。 点物S 象S’ 一个透镜成象的光路 可用两个透镜的作用来 L 等效，如图所示： 等效，如图所示： L1 L2 象 点物就相当于在透 点物 物方焦点处， 镜L1物方焦点处，经通 f1 f2 光孔径A， 光孔径 ，进行夫琅和 费衍射，在透镜L 费衍射，在透镜 2的象 A 方焦点处形成的中央零 仅当通光孔径足够大时， 仅当通光孔径足够大时， 级明斑中心。 级明斑中心。 爱里斑才可能很小。 a >> λ 爱里斑才可能很小。 5
S1 S2
可分辨 此时两爱 里斑重叠 部分的光 强为一个 光斑中心 最大值的 80％。 ％。
S1 S2
恰可分辨
两爱里斑中心距d 恰好等于爱里斑半径。 两爱里斑中心距 0恰好等于爱里斑半径。
S1 S2
不可分辨
7
2.光学仪器分辨率 光学仪器分辨率 满足瑞利判据的两物点间的距离， 满足瑞利判据的两物点间的距离，就是光学仪器 所能分辨的最小距离。 所能分辨的最小距离。此时两个物点对透镜中心所张 的角δϕ称为最小分辨角。 δϕ称为最小分辨角 的角δϕ称为最小分辨角。 d0为光学仪器可分辨的最小距离，即为两物点可 为光学仪器可分辨的最小距离， 分辨的最小距离， 为圆孔到两物点的垂直距离， 分辨的最小距离，L为圆孔到两物点的垂直距离，若为 光学仪器， 即为焦距f 为圆孔直径。 光学仪器，则L即为焦距f。D为圆孔直径。 光学仪器中将最小分辨角的倒数称为仪器的分辨率 光学仪器中将最小分辨角的倒数称为仪器的分辨率。
4
二、光学仪器的分辨本领
一般光学仪器成像， 一般光学仪器成像，光学仪器对点物成象是一个 有一定大小的爱里斑。 有一定大小的爱里斑。 所以由于衍射现象 会使图像边缘变得模糊不清， 由于衍射现象， 所以由于衍射现象，会使图像边缘变得模糊不清， 使图像分辨率下降。 使图像分辨率下降。 点物S 象S’ 一个透镜成象的光路 可用两个透镜的作用来 L 等效，如图所示： 等效，如图所示： L1 L2 象 点物就相当于在透 点物 物方焦点处， 镜L1物方焦点处，经通 f1 f2 光孔径A， 光孔径 ，进行夫琅和 费衍射，在透镜L 费衍射，在透镜 2的象 A 方焦点处形成的中央零 仅当通光孔径足够大时， 仅当通光孔径足够大时， 级明斑中心。 级明斑中心。 爱里斑才可能很小。 a >> λ 爱里斑才可能很小。 5
圆孔衍射衍射光栅
a +b
屏
a
b f
0
x
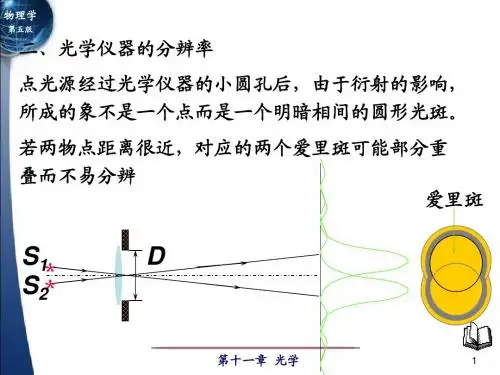
(a+b) sin ——相邻两缝光线的光程差
光栅常数：a+b 数量级为10-5~10-6m
第十一章 光学
8
物理学
第五版
11-9 二、光栅的衍射规律 光栅每个缝形成各自的单缝衍射图样。
衍射光栅
光栅缝与缝之间形成的多缝干涉图样。
光栅衍射条纹是单缝衍射与多缝干涉的总效果。
1、光栅公式
4
0.005 5 cm 0.055 mm
第十一章 光学
5
物理学
第五版
11-9
衍射光栅
一
光栅
由大量等间距、等宽度的平行狭 缝所组成的光学元件。
透射光栅
用于透射光衍射的光栅
第十一章 光学
6
物理学
第五版
11-9
衍射光栅
反射光栅
用于反射光衍射的光栅
第十一章 光学
7
物理学
第五版
11-9
衍射光栅 衍射角
=k'
即
缝间光束干 (a+b)sin 涉极大条件
=k
d k k' ( k' 1,2 , ) a
k 就是所缺的级次
物理学
第五版
11-9
衍射光栅
a 3 当a与b成整数比时,例如 b 5
则有,
d ab 8 k k' k' ( 1 a / b )k' k' a b 5
第十一章 光学
16
物理学
第五版
11-9
衍射光栅
衍射光谱分类 连续光谱：炽热物体光谱 线状光谱：放电管中气体放电 带状光谱：分子光谱
11-8圆孔衍射 光学仪器的分辨率
例1 设人眼在正常照度下的瞳孔直径约 为3 mm，而在可见光中，人眼最敏感的波 长为550 nm，问
(1)人眼的最小分辨角有多大？
(2)若物体放在距人眼25 cm（明视距离） 处，则两物点间距为多大时才能被分辨？
第十一章 光学
11
物理学
第五版
11-8
圆孔衍射
光学仪器的分辨本领
解 (1) 0 1.22
(1)有一毫米波雷达，其圆形天线直径 为55 cm，发射频率为220 GHz的毫米波， 计算其波束的角宽度； (2)将此结果与普通船用雷达发射的波 束的角宽度进行比较，设船用雷达波长为 1.57 cm，圆形天线直径为2.33 m .
第十一章 光学
13
物理学
第五版
11-8
圆孔衍射
光学仪器的分辨本领
解 (1) 雷达波由圆形天线发射，可看成是圆孔的衍射波，
物理学
第五版
11-8
圆孔衍射
光学仪器的分辨本领
一、圆孔的夫琅禾费衍射
实验装置
H
L
P
艾 里 斑
d
光通过圆孔也能产生衍射现象，称为圆孔衍射。
第十一章 光学
1
物理学
第五版
11-8
圆孔衍射
光学仪器的分辨本领
当单色平行光垂直照射到小圆孔时，在位于透镜焦平面处 的屏幕上，将出现环形衍射斑，中央是一个较亮的圆斑，它集 中了全部衍射光强的84%，称为中央亮斑或艾里斑，外围是一 组同心的暗环和明环，且强度随级次增大而迅速下降。 I
1.57102 m 2 2.44 2.44 0.016 4 rad D2 2.33m
第十一章 光学
14
2
9
物理学
11-08圆孔衍射 光学仪器分辨率 (2)
7
2.2 10 rad
（ 2）
4
d l 0 25cm 2.2 10
4
0.0055 cm 0.055mm
§11-8 圆孔衍射
光学仪器的分辨率
例2 毫米波雷达发出的波束比常用的雷达波束窄， 这使得毫米波雷达不易受到反雷达导弹的袭击. （1）有一毫米波雷达，其圆形天线直径为55cm， 发射频率为220GHz的毫米波，计算其波束的角宽度； （2）将此结果与普通船用雷达发射的波束的角宽 度进行比较，设船用雷达波长为1.57cm，圆形天线直 径为2.33m . c 3 108 m/s 3 1 1 . 36 10 m 解（1） 9
光学仪器的分辨率
例1 设人眼在正常照度下的瞳孔直径约为3mm， 而在可见光中，人眼最敏感的波长为550nm，问 （1）人眼的最小分辨角有多大？ （2）若物体放在距人眼25cm（明视距离）处，则 两物点间距为多大时才能被分辨？
1.22 5.5 10 m 解（1） 0 1.22 D 3 103 m
x 0 l
0 1.22
1.2 5.0 10 3 l 8 . 94 10 m 9 1.22 55010
3
§11-8 圆孔衍射
光学仪器的分辨率
三
光学仪器的分辨本领 （两光点刚好能分辨）
光学仪器的通光孔径 D
s1 * s 2*
0
f
d 2 1.22 f D
d
d 2 0 1.22 f D
2
最小分辨角 0 1.22
D
1 D D, 光学仪器分辨率 0 1.22
1.36103 m 1 2.44 2.44 0.00603 rad 2 D1 5510 m 2 1.57102 m 2.44 0.0164 rad （2） 2 2.44 D2 2.33m
14-7 圆孔衍射 光学仪器的分辨率
一
问: 为什么我们看不清远处的物体呢 ？ 圆孔衍射
H
L
P
艾 里 斑
d
L
D
f
P
d ：艾里斑直径
d
d2 1 .22 f D
二
瑞利判据
0 .8 I 0
对于两个强度相等的不相干的点光源（物点）， 一个点光源的衍射图样的主极大刚好和另一点光源衍 射图样的第一极小相重合，这时两个点光源（或物点） 恰为这一光学仪器所分辨.
解 （1）哈勃望远镜的最小分辨角为
1 . 22 7 4 . 0 10 rad D
例 2 太空望远镜 （2）人类正在建造新一代太
空望远镜韦布，计划于2012年利 用欧洲航天局的 “阿丽亚娜5号” 火箭发射, 在距离地球150万公里
的遥远轨道上运行，以代替将要
D D 解 布太空望远镜的主透镜直径至少 1.22
（1）人眼的最小分辨角有多大？
（2）若教室黑板上写有一等于号“＝”，在什么情 况下，距离黑板10m处的学生才不会因为衍射效应，将 等于号“＝”看成减号“－”? 解（1） 0
（ 2） s l
1.22 2 . 2 10rad D
4
2 . 2 mm
0
等号两横线间距不小于 2.2 mm
3 1 1 2 1
例3 毫米波雷达发出的波束比常用的雷达波束窄， 这使得毫米波雷达不易受到反雷达导弹的袭击. （1）有一毫米波雷达，其圆形天线直径为55cm， 发射频率为220GHz的毫米波，计算其波束的角宽度； （2）将此结果与普通船用雷达发射的波束的角宽 度进行比较，设船用雷达波长为1.57cm，圆形天线直 径为2.33m . 8 c 3 10 m/s 3 1 . 36 10 m 解（1） 1 9
问: 为什么我们看不清远处的物体呢 ？ 圆孔衍射
H
L
P
艾 里 斑
d
L
D
f
P
d ：艾里斑直径
d
d2 1 .22 f D
二
瑞利判据
0 .8 I 0
对于两个强度相等的不相干的点光源（物点）， 一个点光源的衍射图样的主极大刚好和另一点光源衍 射图样的第一极小相重合，这时两个点光源（或物点） 恰为这一光学仪器所分辨.
解 （1）哈勃望远镜的最小分辨角为
1 . 22 7 4 . 0 10 rad D
例 2 太空望远镜 （2）人类正在建造新一代太
空望远镜韦布，计划于2012年利 用欧洲航天局的 “阿丽亚娜5号” 火箭发射, 在距离地球150万公里
的遥远轨道上运行，以代替将要
D D 解 布太空望远镜的主透镜直径至少 1.22
（1）人眼的最小分辨角有多大？
（2）若教室黑板上写有一等于号“＝”，在什么情 况下，距离黑板10m处的学生才不会因为衍射效应，将 等于号“＝”看成减号“－”? 解（1） 0
（ 2） s l
1.22 2 . 2 10rad D
4
2 . 2 mm
0
等号两横线间距不小于 2.2 mm
3 1 1 2 1
例3 毫米波雷达发出的波束比常用的雷达波束窄， 这使得毫米波雷达不易受到反雷达导弹的袭击. （1）有一毫米波雷达，其圆形天线直径为55cm， 发射频率为220GHz的毫米波，计算其波束的角宽度； （2）将此结果与普通船用雷达发射的波束的角宽 度进行比较，设船用雷达波长为1.57cm，圆形天线直 径为2.33m . 8 c 3 10 m/s 3 1 . 36 10 m 解（1） 1 9
14-7圆孔衍射 光学仪器分辨率
▲ 在正常照明下，人眼瞳孔直径约为3mm，
对 = 0.55 m（5500A）的黄光， 1，
可分辨约 9m 远处的相距 2mm 的两个点。 ▲ 夜间观看汽车灯，远看是一个亮点， 逐渐 移近才看出是两个灯。
1990 年发射的哈勃
第 十 四 章 波 动 光 学 14-7 圆 孔 衍 射
( 经透 镜 )
二、瑞利判据
第 十 四 章 波 动 光 学 14-7 圆 孔 衍 射
0 .8 I 0
两个点光源（物点）S1和S2的距离恰好使两个艾里斑 中心的距离等于一个艾里斑的半径，即S1艾里斑的 中心正好和S2艾里斑的边缘重叠，这时两个点光源 （或物点）恰为这一光学仪器所分辨.
小孔（直径D）对两个靠近的遥远的点光源的分辨
太空探戈
第 十 四 章 波 动 光 学 14-7 圆 孔 衍 射
例1. 人眼的最小分辨角约为1´，教室中最后一排 的学生对黑板上的两条黄线（5893Å）的最小分 辨距离为多少？并估计瞳孔直径大小。 S1 解：设最后一排同学 * dmin 到黑板距离： * S2 L 15 m
0
0 L
I
当两黄线恰可分辨时，两艾里斑中心到人眼张角 为最小分辨角
太空望远镜的凹面物镜
的直径为2.4m ，最小分
辨角 0 0.1" ，在大气层
外 615km 高空绕地运行 ,
可观察130亿光年远的太
空深处, 发现了500 亿个 星系 .
第 十 四 章 波 动 光 学 14-7 圆 孔 衍 射
棒旋形星系与地球 之间的距离近7000 万光年，是哈勃太 空望远镜拍摄过的 个头最大的星系。 一般的螺旋形星系 的中心是有圆核的， 而棒旋形星系的中 心是棒形状，棒的 两边有旋形的臂向 外伸展。
对 = 0.55 m（5500A）的黄光， 1，
可分辨约 9m 远处的相距 2mm 的两个点。 ▲ 夜间观看汽车灯，远看是一个亮点， 逐渐 移近才看出是两个灯。
1990 年发射的哈勃
第 十 四 章 波 动 光 学 14-7 圆 孔 衍 射
( 经透 镜 )
二、瑞利判据
第 十 四 章 波 动 光 学 14-7 圆 孔 衍 射
0 .8 I 0
两个点光源（物点）S1和S2的距离恰好使两个艾里斑 中心的距离等于一个艾里斑的半径，即S1艾里斑的 中心正好和S2艾里斑的边缘重叠，这时两个点光源 （或物点）恰为这一光学仪器所分辨.
小孔（直径D）对两个靠近的遥远的点光源的分辨
太空探戈
第 十 四 章 波 动 光 学 14-7 圆 孔 衍 射
例1. 人眼的最小分辨角约为1´，教室中最后一排 的学生对黑板上的两条黄线（5893Å）的最小分 辨距离为多少？并估计瞳孔直径大小。 S1 解：设最后一排同学 * dmin 到黑板距离： * S2 L 15 m
0
0 L
I
当两黄线恰可分辨时，两艾里斑中心到人眼张角 为最小分辨角
太空望远镜的凹面物镜
的直径为2.4m ，最小分
辨角 0 0.1" ，在大气层
外 615km 高空绕地运行 ,
可观察130亿光年远的太
空深处, 发现了500 亿个 星系 .
第 十 四 章 波 动 光 学 14-7 圆 孔 衍 射
棒旋形星系与地球 之间的距离近7000 万光年，是哈勃太 空望远镜拍摄过的 个头最大的星系。 一般的螺旋形星系 的中心是有圆核的， 而棒旋形星系的中 心是棒形状，棒的 两边有旋形的臂向 外伸展。
大学物理第7章第7节-圆孔缝夫琅禾费衍射及光学仪器的分辨率
a
b
(a) 可分辨
b
a a
b
0
(b) 恰能分辨
(c) 不能分辨
光学仪器分辨率 (瑞利判据): 其中一个 艾里斑的极大处刚好落在另一个艾里斑的 极小处时, 光学仪器恰好能够分辨出是两个 点.
b
a
0
(b) 恰能分辨
光学仪器的最小分辨角: 在满足瑞利判 据的条件下两物点对透镜光心的张角
0 1.22
7.7 圆孔夫琅禾费衍射 及光学仪器的分辨率
一. 圆孔衍射 将单缝夫琅禾费单缝衍 射中的狭缝换成圆孔, 在屏 上观察到明暗相间的同心圆 环形衍射条纹, 即圆孔夫琅禾 费衍射图样. 在中央处为一个圆形亮斑, 称 为艾里斑.
圆孔夫琅禾费衍射图样的强度分布 当 0 时为中央极大, 以中央极大对称分布的艾 里斑的光强最大, 占入射光 I I 强度的 83.78%.
f N D f 200103 0.05m D N 4
镜头的最小分辨角
0 1.22
9
D
55010 5 1 . 34 10 rad 1.22 0.05
镜头能分辨出前方10m处的两物点最 小距离
0
l
r
l r 0 10 1.34 105
1.34 104 m 0.134mm
对人眼, 最小分辨角为
55010 4 1 . 34 10 rad 0 1.22 1.22 3 D 5 10
9
眼睛能分辨出前方10m处的两物点最 小距离
0
l
r
l r 0 10 1.34 104 1.34 103 m 1.34mm
1
D
大学物理第12讲：10.4 圆孔衍射、光学仪器的分辨率
4、分辨本领： 最小分辨角的倒数
1 D 1 1.22 1
5、人眼的分辨本领
5 107 4 0 1.22 1.22 1 . 22 10 rad 3 D 5 10
思考： 望远镜的分辨本领？
显微镜的分辨本领？
课堂练习2：在迎面驶来的汽车上，两盏前灯相距120cm，设夜 间人眼瞳孔直径为5.0mm，入射光波长为500nm，问汽车离人多 远的地方，眼睛恰可分辨这两盏灯？
欧洲南方天文台将在智利阿塔卡玛沙漠建造世界最大 的天文望远镜。该望远镜镜片直径是一座足球场长度的一 半，它对可见光和红外线的灵敏度将是现存望远镜的十倍 。天文学家希望，这座望远镜能帮助人们破解有助于解释 宇宙演化的暗物质秘密，甚至能探测到外星人的行踪。 2020年前投入使用
1990 年发射的哈勃太空望远镜的凹面物镜的直径为2.4m ，最小分辨角 0.1'' ，在大气层外615km 高空绕地运行 , 可观察130亿光年远的太空深处, 发现了500 亿个星系 .
英豪天文台卡塞格林折反射光路的500毫米望 远镜，是目前华南地区最大的天文望远镜。
中国将在贵州建造世界上最大的望远镜
中国十一五期间，将投资60亿元用于十二项大科学工程 的建设，并将在贵州建造世界上最大的望远镜，它将使中国
的天文观测能力延伸到宇宙边缘，寻找第一代诞生的天体。
智利阿塔卡玛沙漠建造世界最大望远镜
显镜的分辨本领
最小分辨角 对于显微镜，孔径一 定，波长越短，分辨率 就越高，看得越细微。
1 D 1 1.22
1
孔径
波长
X射线的衍射
小 结：
1、圆孔衍射 2、光学仪器的分辨能力
作 业：
1、仔细阅读教材；
第17讲 圆孔衍射,分辨率,x射线衍射
三、布拉格公式 布拉格反射
1913年，英国布
拉格父子提出了一种 解释Ｘ射线衍射的方 法，给出了定量结果， 并于1915年荣获诺贝
入射波
散射波
o
C
B
d
A
尔物理学奖。
2 d sin 或离子中的电子在 外场作用下做受迫振动。
晶体中的 原子或离子
晶体点阵 中的每一阵 点可看作一 个新的波源， 向外辐射与 入射的 X 射 线同频率的 电磁波，称 为散射波。
X射线
晶体点阵的散射波可以相互干涉。
包括
面中点阵
散射波干涉
和
面间点阵
散射波干涉
2、任一平面上的点阵散射波的干涉
入射 X射线
平面法线
镜面反射方向
入射角
掠射角
任一平面 上的点阵
干涉结果总是在镜面反射方向上出现最大光强。
3、面间点阵散射波的干涉
入射角 掠射角 求出相邻晶面距 离为 d 的两反射 光相长干涉条件
X 射线的衍射
伦 琴 （W. K. Rontgen， 1845-1923）
德国实验物理学家，1895年发现了X射线，并 将其公布于世。历史上第一张X射线照片，就是伦 琴拍摄他夫人的手的照片。 由于X射线的发现具有重大的理论意义和实用 价值，伦琴于1901年获得首届诺贝尔物理学奖。
劳厄（M. V. Laue，1879-1960） 德国物理学家，发现 X射线 的衍射现象，从而判定X射线的 本质是高频电磁波。1904年，他 因此获得诺贝尔物理学奖。 布拉格父子（W. L. Bragg，子、W. H. Bragg，父）
第一暗环对应的衍射角 称为爱里斑的半角宽，
d 2 f
1 . 22
14-7 圆孔衍射 光学仪器的分辨率
第十四章 波动光学
2
14 – 7 圆孔衍射 光学仪器分辨率
物理学教程 （第二版）Βιβλιοθήκη 一圆孔衍射H
L
P
艾 里 斑
d 2 sin 1.22 / D f
d
d
第一暗环所围成的中 央光斑称为爱里斑
L
D
f
第十四章 波动光学
P
爱里斑半径d /2 对透镜 光心的张角称为爱里斑 的半角宽度
14 – 7 圆孔衍射 光学仪器分辨率 二、光学仪器的分辨率 （两光点刚好能分辨）
物理学教程 （第二版）
点光源经过光学仪器的小圆孔后，由于衍射的影响， 所成的象不是一个点而是一个明暗相间的圆形光斑。 若两物点距离很近，对应的两个爱里斑可能部分重 叠而不易分辨 爱里斑
S1 * S2*
D
第十四章 波动光学
14 – 7 圆孔衍射 光学仪器分辨率 瑞利判据
物理学教程 （第二版）
0.8I 0
物理学教程 （第二版）
例1 设人眼在正常照度下的瞳孔直径约为3mm， 而在可见光中，人眼最敏感的波长为550nm，问
（1）人眼的最小分辨角有多大？ （2）若物体放在距人眼25cm（直视距离）处， 则两物点间距为多大时才能被分辨？ 1.22 5.5 10 7 m 4 1 . 22 2.2 10 rad 解（1） 0 3 D 3 10 m 0 4 （2）d 2l tan 0.055 mm l 0 25cm 2.2 10
例 用一定波长的光通过光学仪器观察物体
（1）物体大时，分辨率大
（2）物体离光学仪器远时分辨率大
（3）光学仪器的孔径愈小分辨率愈小
（4）物体近时分辨率大
D 1 D, 光学仪器分辨率 0 1.22
2
14 – 7 圆孔衍射 光学仪器分辨率
物理学教程 （第二版）Βιβλιοθήκη 一圆孔衍射H
L
P
艾 里 斑
d 2 sin 1.22 / D f
d
d
第一暗环所围成的中 央光斑称为爱里斑
L
D
f
第十四章 波动光学
P
爱里斑半径d /2 对透镜 光心的张角称为爱里斑 的半角宽度
14 – 7 圆孔衍射 光学仪器分辨率 二、光学仪器的分辨率 （两光点刚好能分辨）
物理学教程 （第二版）
点光源经过光学仪器的小圆孔后，由于衍射的影响， 所成的象不是一个点而是一个明暗相间的圆形光斑。 若两物点距离很近，对应的两个爱里斑可能部分重 叠而不易分辨 爱里斑
S1 * S2*
D
第十四章 波动光学
14 – 7 圆孔衍射 光学仪器分辨率 瑞利判据
物理学教程 （第二版）
0.8I 0
物理学教程 （第二版）
例1 设人眼在正常照度下的瞳孔直径约为3mm， 而在可见光中，人眼最敏感的波长为550nm，问
（1）人眼的最小分辨角有多大？ （2）若物体放在距人眼25cm（直视距离）处， 则两物点间距为多大时才能被分辨？ 1.22 5.5 10 7 m 4 1 . 22 2.2 10 rad 解（1） 0 3 D 3 10 m 0 4 （2）d 2l tan 0.055 mm l 0 25cm 2.2 10
例 用一定波长的光通过光学仪器观察物体
（1）物体大时，分辨率大
（2）物体离光学仪器远时分辨率大
（3）光学仪器的孔径愈小分辨率愈小
（4）物体近时分辨率大
D 1 D, 光学仪器分辨率 0 1.22
10-6圆孔衍射光学仪器的分辨率.ppt
10-6 圆孔衍射 光学仪器的分辨率 光学仪器的通光孔径 D
s1* s2*
0
d
f
最小分辨角 0 1.22 D 光学仪器分辨率
2
1 D 0 1 .2 2
10-6 圆孔衍射 光学仪器的分辨率 思考 例 用一定波长的光通过光学仪器观察物体
（A）物体大时，分辨率大
（B）物体离光学仪器远时分辨率大
（C）光学仪器的孔径愈小分辨率愈小
（D）物体近时分辨率大
10-6 圆孔衍射 光学仪器的分辨率
m m 例10-2 通常人眼瞳孔的直径约为 2 3 ，在明 亮的环境中，对于人眼最敏感的是波长为 550nm 的 n 1.34 黄绿光，人眼中玻璃液的折射率为 。求： (1)人眼的最小分辨角； (2)若物体放在明视距离 25cm 处，则两物点至少相 距多少时才能被分辨。
解 (1)
最小分辨角
4 . 1 0 1 0m n = n 4 n 1 . 2 2 2 . 5 01 0r a d
7
0
D
r0 (2) 0 l
r l 6 . 2 51 0m 0 0
5
10-6 圆孔衍射 光学仪器的分辨率
பைடு நூலகம்
一、夫琅禾费圆孔衍射
H
L
P
艾 里 斑
d
L
D
f
P
d
d
：艾里斑直径
d 2 2.44 f D
10-6 圆孔衍射 光学仪器的分辨率
二、光学仪器的分辨本领
瑞利判据
0 .8 I 0
对于两个强度相等 的不相干的点光源（物 点），一个点光源的衍 射图样的主极大刚好和 另一点光源衍射图样的 第一极小相重合，这时 两个点光源（或物点） 恰为这一光学仪器所分 辨.
《大学物理III》教学大纲和考试大纲-64学时
《大学物理Ⅲ》课程简介课程名称：《大学物理Ⅲ》/College Physics Ⅲ课程代码：学时/学分：64/4课堂授课：64课程主要内容：本课程主要讲授力学、相对论、振动与波、波动光学、量子物理基础。
从经典力学拓宽到相对论力学；从宏观物体的运动学、动力学规律到三大守恒定律在宏观世界的应用；光的干涉、衍射及偏振现象与规律；普朗克量子假说、光的波粒二象性、德布罗意物质波及其统计解释、不确定关系、玻尔的氢原子理论，薛定谔方程及其初步应用等。
适用专业：先修课程：《高等数学》推荐教材：1．赵近芳王登龙编，《大学物理学》（第4版），北京邮电大学出版社，2014年。
参考书：1．张三慧主编，《大学基础物理学》，清华大学出版社，2003年；2．程守洙、江之永主编，《普通物理学》第5版，高等教育出版社，2001年；3、卢德馨主编，《大学物理学》，高等教育出版社，1998年；4．R.P.费曼，《费曼物理学讲义》，上海科学技术出版社，1983年；5．郭奕玲、沈慧君编著，《物理学史》，清华大学出版社，2005年。
《大学物理Ⅲ》课程教学大纲授课专业：学时数：64；学分数：4.0一、课程的性质和目的本课程是非物理专业的基础课程。
本课程的任务是通过讲授和讨论力学、相对论、振动与波、波动光学、量子物理基础等基础知识，使学生掌握力学、波动光学和近代物理的基本体系，认识光在传播过程中表现出的波动性以及在科学技术中的应用；了解量子力学的形成过程与基本规律，以及在微观领域所取得的巨大成就；了解物理学的新成就和发展方向，拓展学生视野，培养学生的创新意识，为后续课程的学习和将来进一步发展奠定良好的物理基础。
二、课程教学的基本要求本课程的教学环节以课堂讲授为主，辅以习题讨论、答疑、学生自学、课后作业、小测验和期末考试；通过上述教学环节，使学生学会从观察自然现象和总结实验事实入手，利用物理模型，掌握三大守恒定律在力学中的应用；理解经典时空观和相对论时空观的区别。
第4章光的衍射
• 教学难点：圆孔衍射；衍射光栅
• 教学目的：
• 1.重点掌握单缝夫琅禾费衍射的基本原理；
• 2.掌握光学仪器的分辨本领及相关计算；
• 3.了解圆孔衍射和衍射光栅及其应用。
第 4 章 光的衍射
• 当光遇到小孔、狭缝或其他的很小障碍物时，传播方向将 发生偏转，而绕过障碍物继续前行，并在光屏上形成明暗 相间的圆环或条纹。光波的这种现象称为光的衍射，也称 为光的绕射。
12k22k1112 450nm
• 例4-1 如图所示，用波长λ=0.5μm 的单色平行光
，垂直照射到缝宽为 a=0.5mm 的单缝上，在缝 后放置一个焦距为 f=0.5m的凸透镜，求在屏上
• （1）中央明纹的宽度;（2）第1级明纹的宽度。 • •
•
• 解（1）由单缝衍射的明、暗纹条件可知，中央明纹 的宽度为k=-1与k=1级暗纹之间的距离.
• 本章将基于惠更斯－菲涅耳原理，利用半波带法，重点分 析夫琅禾费单缝衍射和光栅衍射的性质，讨论人眼和光学 助视仪器的分辨本领。
4.1 光的衍射
• 4.1.1 衍射的分类 • 4.1.2 惠更斯—菲涅耳原理
4.1.1 衍射的分类
光的衍射现象通常分为两类：夫琅禾费衍射和菲涅耳衍射。 菲涅耳衍射指的是光源 、观察屏 （或者是两者之一）到衍 射屏 的距离是有限的，因而这类衍射又称为近场衍射； 夫琅禾费衍射指的是光源 、观察屏 到衍射屏 的距离均为无 限远，这类衍射也称为远场衍射。
asin 2k1
2
2 k 1 1 1 2 k 2 1 2
• 在两明纹级次和其中一种波长已知的情况下，即可求出另 一种未知波长。
4.2.2 菲涅耳半波带法
• 解：根据题意和分析，将
7.7 圆孔夫琅禾费衍射及光学仪器的分辨率
0 1.22 / DBiblioteka 最小分辨角的倒数1
0
称为光学仪器的分辨率
1 D 0 1.22
D为光学仪器的透光孔径
S1 * S2 *
D
瑞利判据：如果一个点光源的衍射图象的中央最亮处刚 好与另一个点光源的衍射图象第一个最暗处相重合，认 为这两个点光源恰好能为这一光学仪器所分辨。 恰 能 分 辨 能 分 辨 不 能 分 辨
s1 * s2 *
D
0
在恰能分辨时，两个点光源在透镜前所张的角度， 称为最小分辨角0 ，等于爱里斑的半角宽度。
7.7 圆孔夫琅和费衍射
一、圆孔衍射
S
D
第一暗环所围成的中央光斑称为爱里斑 爱里斑半径d 对透镜光心的张角称为爱里斑的半角宽度
d 2 sin 1.22 / D
二、光学仪器的分辨率
点光源经过光学仪器的小圆孔后，由于衍射的影响， 所成的象不是一个点而是一个明暗相间的圆形光斑。 若两物点距离很近，对应的两个爱里斑可能部分重 叠而不易分辨 爱里斑
波动光学第4讲圆孔夫琅禾费衍射光学仪器的分辨本领光栅衍射
轮廓线
光强分布曲线
0
4
8 sin( /d )
5.缺级现象
光栅衍射加强条件
dsink k0,1,2,3,...
单缝衍射减弱条件
asin k k1,2,3,...
这样的主极大是不存在的, 称作缺级现象
两式相除 d k a k
k d k a
所缺级次
k1,2,3,...
光强曲线
I I0
N=4
-2(/d) -(/d-)(/4d)0/4d /d
I0 I单
单
sin
2/d
理论计算 多缝干涉 和单缝衍射 共同决定的 光栅衍射 光强分布 曲线如图
-2
-
1
光栅衍射 光强曲线
-
-4
8
0
1
2 sin ( /a)
I N2I0单
N=4
主极大外形包络线
单缝衍射 d = 4a 为单缝衍射
例1：分光计作光栅实验，用波长 = 632.8 nm的激光照射光栅常数 d = 1/300 mm的光栅
上，问最多能看到几条谱线。
解：在分光计上观察 谱线，最大衍射角为 90°,
d
(ab)sin k
(ab)si9n0
kmax
o
x
fP
kma x(ab)si9 n0
◆采用波长较短的光，也可提高分辨率。
电子显微镜用 加速的电子束代替光束， 其波长约 0.1nm，用它 来观察分子结构。
电子显微镜拍摄的照片
第4节 光栅衍射
一．光栅和光栅常数
1.光栅 由大量彼此互相平行等间隔的透光（或反 射光）的缝组成的光学器件。
透射式光栅
玻璃上刻出等宽等间距的刻痕，刻痕不透光
39圆孔衍射 光学仪器的分辨率
瑞利判据对于两个强度相等的不相干的点光源
（物点），一个点光源的衍射图样的主极大刚好 和另一点光源衍射图样的第一极小相重合，这时 两个点光源（或物点）恰为这一光学仪器所分辨.
三
光学仪器的分辨本领
光学仪器: 望远镜、照相机、眼睛等。 分辨本领：仪器对两相邻点物产生分开像的能力的 衡量。（由于光的波动性，所有光学仪器的分辨本 领都存在一个极限）
11
11-8 圆孔衍射 光学仪器的分辨率
解 (1)
1 2 . 44
1
c
3 10 m/s
8
220 10 Hz
9
1 . 36 10
3
m
ห้องสมุดไป่ตู้
1
D1
2 . 44
1 . 36 10 55 10
3
m
2
0 . 00603 rad
m
(2)
2 2 . 44
2
D2
2 . 44
1 . 57 10
2
m
0 . 0164 rad
2 . 33 m
12
D
4
1 . 22 5 . 5 10 3 10
3
7
m
m
4
2 . 2 10
rad
(2)
d l 0 25 cm 2 . 2 10
0 . 0055 cm 0.055mm
10
11-8 圆孔衍射 光学仪器的分辨率
例2 毫米波雷达发出的波束比常用的 雷达波束窄，这使得毫米波雷达不易受到 反雷达导弹的袭击. (1)有一毫米波雷达，其圆形天线直径 为55cm，发射频率为220GHz的毫米波，计 算其波束的角宽度； (2)将此结果与普通船用雷达发射的波 束的角宽度进行比较，设船用雷达波长为 1.57cm，圆形天线直径为2.33m .
园孔的衍射
在恰能分辨时，两个点光源在透镜前所 张的角度，称为最小分辨角 δφ 。 圆孔衍射的第一级极小值由下式给出：
sin 1 =1.22 λ θ D
s1 * s2 *
D
δφ
在恰能分辨时，两个点光源在透镜前所 张的角度，称为最小分辨角 δφ 。 圆孔衍射的第一级极小值由下式给出：
sin 1 =1.22 λ θ D 最小分辨角为：
sin 1 =1.22 λ θ D 最小分辨角为： δφ = sin 1 ~ 1 θ θ
s1 * s2 *
D
δφ
在恰能分辨时，两个点光源在透镜前所 张的角度，称为最小分辨角 δφ 。 圆孔衍射的第一级极小值由下式给出：
sin 1 =1.22 λ θ D 最小分辨角为： δφ = sin 1 ~ 1 = 1.22 λ θ θ D
五、光学仪器的分辨率 点光源经过光学仪器的小圆孔后，由于 衍射的影响，所成的象不是一个点而是一个 明暗相间的圆形光斑。 中央最亮的亮斑称为爱里斑。
爱里斑 s1 * s2 * D δφ
瑞利判据：如果一个点光源的衍射图象的中 央最亮处刚好与另一个点光源的衍射图象第 一个最暗处相重合，认为这两个点光源恰好 能为这一光学仪器所分辨。
s1 * s2 *
D
δφ
在恰能分辨时，两个点光源在透镜前所 张的角度，称为最小分辨角 δφ 。 圆孔衍射的第一级极小值由下式给出：
sin 1 =1.22 λ θ D 最小分辨角为： δφ = sin 1 θ
s1 * s2 *
D
δφ
在恰能分辨时，两个点光源在透镜前所 张的角度，称为最小分辨角 δφ 。 圆孔衍射的第一级极小值由下式给出：
一、圆孔的夫朗和费衍射 实验装置
* S
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
解 （1）哈勃望远镜的最小分辨角为
1.22 4.0 107 rad
D
第十四章 波动光学
14 – 7 圆孔衍射 光学仪器分辨率
物理学教程 （第三版）
例 2 太空望远镜 （2）人类正在建造新一代太空望远镜詹姆斯 韦布，
计划于2018年利用欧洲航天局的 “阿丽亚娜5号”火箭
发射, 在距离地球150万公里的遥远轨道上运行，以代
1.36 10 3 m
1
2.44
1
D1
2.44
1.36103 m 55102 m
0.0062
D2
0.0164 rad
第十四章 波动光学
等号两横线间距不小于 2.2 mm
第十四章 波动光学
14 – 7 圆孔衍射 光学仪器分辨率
物理学教程 （第三版）
例2 太空望远镜 （1）哈勃太空望远镜是1990 年发射升空的天文望远镜 ，它的
主透镜直径为 2.4m , 是目前太 空中的最大望远镜 . 在大气层外 615km高空绕地运行 , 可观察 130 亿光年远的太空深处, 发现了500 亿个星系 . 试计算哈勃 望远镜对波长为 800nm 的红外光的最小分辨角.
14 – 7 圆孔衍射 光学仪器分辨率
物理学教程 （第三版）
例1 设人眼在正常照度下的瞳孔直径约为 D 3mm,
而在可见光中，对人眼最敏感的波长为550nm，问
（1）人眼的最小分辨角有多大？
S*
*
L
解（1） 0
1.22
D
2.2104 rad
第十四章 波动光学
14 – 7 圆孔衍射 光学仪器分辨率
第十四章 波动光学
14 – 7 圆孔衍射 光学仪器分辨率
物理学教程 （第三版）
三 光学仪器的分辨率 （两光点刚好能分辨）
光学仪器的通光孔径 D
s1 *
0
s 2*
f
d 2 1.22
f
D
d 2
0
d2 f
1.22
D
最小分辨角 0
1.22
D
光学仪器分辨率 1 D D, 1
0 1.22
第十四章 波动光学
物理学教程 （第三版）
例1 设人眼在正常照度下的瞳孔直径约为 D 3mm,
而在可见光中，对人眼最敏感的波长为550nm，问 （2）若教室黑板上写有一等于号“＝”，在什么情
况下，距离黑板10m处的学生才不会因为衍射效应，将 等于号“＝”看成减号“－”?
S*
*
L
解 0 2.2 104 rad
（2） s L0 2.2mm
14 – 7 圆孔衍射 光学仪器分辨率
物理学教程 （第三版）
问: 为什么我们看不清远处的物体呢 ？
一 圆孔衍射
HP
L
艾
里
斑
d
L
D
P
d
f
第十四章 波动光学
d ：艾里斑直径
d 2 1.22
f
D
14 – 7 圆孔衍射 光学仪器分辨率 二 瑞利判据
物理学教程 （第三版）
0.8I0
对于两个强度相等的不相干的点光源（物点）， 一个点光源的衍射图样的主极大刚好和另一点光源衍 射图样的第一极小相重合，这时两个点光源（或物点） 恰为这一光学仪器所分辨.
这使得毫米波雷达不易受到反雷达导弹的袭击. （1）有一毫米波雷达，其圆形天线直径为55cm，
发射频率为220GHz的毫米波，计算其波束的角宽度；
（2）将此结果与普通船用雷达发射的波束的角宽
度进行比较，设船用雷达波长为1.57cm，圆形天线直
径为2.33m .
解（1） 1
c
3108 m/s 220 109 Hz
替将要退役的哈勃望远镜 . 设计中的詹姆斯韦布太空
望远镜的主透镜直径至少为 6m , 也可在红外频率下工
作，问与哈勃望远镜相比韦布望远镜的分辨率预计可
以提高多少倍？
解 1 D D
1.22
提高的倍数为
D 2.5 D
第十四章 波动光学
14 – 7 圆孔衍射 光学仪器分辨率
物理学教程 （第三版）
例 毫米波雷达发出的波束比常用的雷达波束窄，
1.22 4.0 107 rad
D
第十四章 波动光学
14 – 7 圆孔衍射 光学仪器分辨率
物理学教程 （第三版）
例 2 太空望远镜 （2）人类正在建造新一代太空望远镜詹姆斯 韦布，
计划于2018年利用欧洲航天局的 “阿丽亚娜5号”火箭
发射, 在距离地球150万公里的遥远轨道上运行，以代
1.36 10 3 m
1
2.44
1
D1
2.44
1.36103 m 55102 m
0.0062
D2
0.0164 rad
第十四章 波动光学
等号两横线间距不小于 2.2 mm
第十四章 波动光学
14 – 7 圆孔衍射 光学仪器分辨率
物理学教程 （第三版）
例2 太空望远镜 （1）哈勃太空望远镜是1990 年发射升空的天文望远镜 ，它的
主透镜直径为 2.4m , 是目前太 空中的最大望远镜 . 在大气层外 615km高空绕地运行 , 可观察 130 亿光年远的太空深处, 发现了500 亿个星系 . 试计算哈勃 望远镜对波长为 800nm 的红外光的最小分辨角.
14 – 7 圆孔衍射 光学仪器分辨率
物理学教程 （第三版）
例1 设人眼在正常照度下的瞳孔直径约为 D 3mm,
而在可见光中，对人眼最敏感的波长为550nm，问
（1）人眼的最小分辨角有多大？
S*
*
L
解（1） 0
1.22
D
2.2104 rad
第十四章 波动光学
14 – 7 圆孔衍射 光学仪器分辨率
第十四章 波动光学
14 – 7 圆孔衍射 光学仪器分辨率
物理学教程 （第三版）
三 光学仪器的分辨率 （两光点刚好能分辨）
光学仪器的通光孔径 D
s1 *
0
s 2*
f
d 2 1.22
f
D
d 2
0
d2 f
1.22
D
最小分辨角 0
1.22
D
光学仪器分辨率 1 D D, 1
0 1.22
第十四章 波动光学
物理学教程 （第三版）
例1 设人眼在正常照度下的瞳孔直径约为 D 3mm,
而在可见光中，对人眼最敏感的波长为550nm，问 （2）若教室黑板上写有一等于号“＝”，在什么情
况下，距离黑板10m处的学生才不会因为衍射效应，将 等于号“＝”看成减号“－”?
S*
*
L
解 0 2.2 104 rad
（2） s L0 2.2mm
14 – 7 圆孔衍射 光学仪器分辨率
物理学教程 （第三版）
问: 为什么我们看不清远处的物体呢 ？
一 圆孔衍射
HP
L
艾
里
斑
d
L
D
P
d
f
第十四章 波动光学
d ：艾里斑直径
d 2 1.22
f
D
14 – 7 圆孔衍射 光学仪器分辨率 二 瑞利判据
物理学教程 （第三版）
0.8I0
对于两个强度相等的不相干的点光源（物点）， 一个点光源的衍射图样的主极大刚好和另一点光源衍 射图样的第一极小相重合，这时两个点光源（或物点） 恰为这一光学仪器所分辨.
这使得毫米波雷达不易受到反雷达导弹的袭击. （1）有一毫米波雷达，其圆形天线直径为55cm，
发射频率为220GHz的毫米波，计算其波束的角宽度；
（2）将此结果与普通船用雷达发射的波束的角宽
度进行比较，设船用雷达波长为1.57cm，圆形天线直
径为2.33m .
解（1） 1
c
3108 m/s 220 109 Hz
替将要退役的哈勃望远镜 . 设计中的詹姆斯韦布太空
望远镜的主透镜直径至少为 6m , 也可在红外频率下工
作，问与哈勃望远镜相比韦布望远镜的分辨率预计可
以提高多少倍？
解 1 D D
1.22
提高的倍数为
D 2.5 D
第十四章 波动光学
14 – 7 圆孔衍射 光学仪器分辨率
物理学教程 （第三版）
例 毫米波雷达发出的波束比常用的雷达波束窄，