点的复合运动2011b

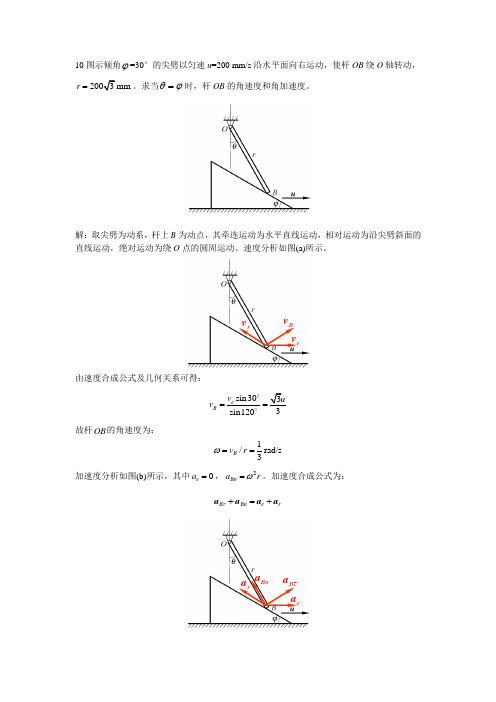
10图示倾角ϕ=30°的尖劈以匀速u =200 mm/s 沿水平面向右运动，使杆OB 绕O 轴转动，

mm r =。求当ϕθ=时，杆OB 的角速度和角加速度。

解：取尖劈为动系，杆上B 为动点，其牵连运动为水平直线运动，相对运动为沿尖劈斜面的直线运动，绝对运动为绕O 点的圆周运动。速度分析如图(a)所示。

e

v B v r

v

由速度合成公式及几何关系可得：

sin 30sin120e B v v ==

故杆OB 的角速度为：

1/rad/s 3

B v r ω==

加速度分析如图(b)所示，其中0e a =，2Bn a r ω=。加速度合成公式为：

B Bn e r τ+=+a a a a

e

a B τa r

a Bn

a

将上式向垂直于r a 的方向投影，得：

sin30cos300Bn B a a τ+=

2B a r τ= 故杆OB 的角加速度为：

2rad/s B a r τε=

= （顺时针）

12小环M 同时与半径为r 的两圆环如图相交，圆O ' 固定，圆环O 绕其圆周上一点A 以匀角速度ω转动。求当A 、O 、O ' 位于同一直线时两圆环交点M 的速度大小与加速度大小。

解： 取圆环O 为动系，M 点为动点，牵连运动为绕A 点的圆周运动，相对运动为沿圆环O

的圆周运动，绝对运动为沿则圆O ' 的圆周运动，速度分析如图(a)所示，其中e v ω。由几何关系可知，30MAO MBO '∠=∠= ，60MO O '∠= ，连线AM 为圆O '的切线，MB 为圆O 的切线。

v

e

v r

v B

(a)

速度合成公式为：

e r =+v v v （1）

因此有：

cot 60e v v r ω== /cos602r v v r ω==

加速度分析如图(b)所示，其中2

e a ω=，2

4c a r ω=，22

4r rn v a r r ω==，22n v a r r

ω==。

a τa r τ

a B

n

a e c

a rn

a

(b)

加速度合成公式为：

n e r rn c ττ+=+++a a a a a a

（2） 将上式向rn a 方向投影，得：

cos30cos60cos30n e rn c a

a a a a τ-+=+-

解得：

2

a τω= 因此M 点的加速度的大小为

2

a ω=

13OA 杆以等角速度0ω绕O 轴转动，半径为r 的滚轮在OA 杆上作纯滚动，已

知

r B O 31=，图示瞬时O 、B 在同一水平线上，B O 1在铅垂位置，︒=∠30AOB ，求在此瞬时：（1）B O 1杆的角速度与角加速度；（2）滚轮的角速度与角加速度；（3）滚轮上P 点

的速度与加速度。

解：建立如图所示的动系11Ox y ，坐标轴的单位矢量分别记为1i 和1j 。取OA 杆为动系，B 点为动点，牵连运动为定轴转动，相对运动为平行于1x 方向的直线运动，绝对运动为绕

1O 点的圆周运动，如图(a)所示，其中02e v r ω=。

B v r

v e

v

(a)

由速度合成关系可得：

04r v r ω=，0B v ω=。

由此可得：

1

012B

O B v O B

ωω=

= （逆时针） 以点B 为基点分析P 点运动，得到：

1+

P B B r ω=ννi

由于轮作纯滚动，故01P v r j 。将上式向1x 轴方向投影，得：

0cos30B B v r ω=+

故有：

03B ωω=-（顺时针）

加速度分析如图(b)所示，其中202e a r ω=，2

8c a r ω=，22

1B Bn v a O B

ω==。 B τa r

a Bn

a e

a c

a

加速度合成公式为：

Bn B r e c τ+=++a a a a a

将上式向c a 方向投影，得：

cos30cos60cos60Bn B e c a a a a

τ+=-+

解得：

20

2B a r τω= 因此得

1

2

01B O B a O B

τεω=

= （逆时针） 以B 为基点，分析P 点的加速度，有：

2

11P B Bn B B r r τωε=+++a a a j i

由于轮作纯滚动，轮上P 点和其在杆上的接触点的加速度在1x 方向的分量相同，故有

2

011P Py a ω=+a i j 。将上式分别向1x 和1y 轴方向投影，得：

2

0cos30cos60B Bn B a a r τωε=-+

2

cos60cos30Py B Bn B

a a a r τω=++ 解得：

0B ε=，2

16Py a r ω=

答： （1）102O B ωω=（逆时针），12

0O B ε=

（逆时针） （2）03B ωω=（顺时针），0B ε=

（3）01P ω=v j ，()

2

116P r ω=+a j

17图示机构中，小环M 套在直角曲杆AB O 1上，同时还套在半径为r 的半圆环上，当半圆

环以水平速度0v 、水平加速度0a 行至图示位置时，︒=30θ，且知AM ，曲杆绕1

O 轴转动的角速度为1ω，角加速度为零，试求此瞬时小环M 的速度和加速度。

解：由几何关系可知1O A =

，3

2

AM r ==，112O M O A ==。 1.求速度。

取曲杆AB O 1为动系，小环M 为动点，牵连运动为定轴转动，相对运动为沿AB 的直线

运动。牵连速度和相对速度分别记为e v 和r v ，其中1e v ω。如图(a)所示。

e

v 30

r

v e

'v r 'v

(a)

速度合成公式为：

M e r +v =v v (a)

式(a)有三个未知数，不能直接求解。

取半圆环为动系，小环M 为动点，牵连运动为水平方向的平动，相对运动为沿半圆环

的圆周运动，牵连速度和相对速度分别记为e 'v 和r 'v ，其中0v v '

e =。如图(a)所示。

速度合成公式为：

M e

r ''+v =v v (b)