点的复合运动
点的复合运动

点的合成运动
y’
o’
x’
例2、直升飞机在匀速前进的军舰上降落
y
y’
o’
x’
x
o
点的合成运动
y’ x’
o’
物体的运动的描述结果与所选定的参考系有关。同一物体的运动,在不同的 参考系中看来,可以具有极为不同的运动学特征(具有不同的轨迹、速度、 加速度等)。
相对运动:未知
3、
va ve vr
大小 v1 v2
?
方向 √ √
?
vr va2 ve2 2vave cos60 3.6 m s
arcsin(ve sin 60o ) 46o12
点的合成运动
vr
求解合成运动的速度问题的一般步骤为(P180):
① 选取动点,动系和静系。
B
曲柄-滑块机构
点的合成运动
思考题 动 点:杆上A点。 动系:固连于滑块B。 定系:固连于墙面。 绝对运动? 相对运动? 牵连运动?
点的合成运动
A Bv
点的合成运动
动 点? 动参考系? 绝对运动? 相对运动? 牵连运动?
练习题1
点的合成运动
点的合成运动
点的合成运动
动 点? 动参考系? 绝对运动? 相对运动? 牵连运动?
定系的速度。
点的合成运动
基本概 念
牵连点的概念
(1)、定 义 动参考系给动点直接影响的是该动系上与动点相重合的一点,
这点称为瞬时重合点或动点的牵连点。 (2)、进一步说明
牵连运动一方面是动系的绝对运动,另一方面对动点来说起 着“牵连”作用。但是带动动点运动的只是动系上在所考察的瞬 时与动点相重合的那一点,该点称为瞬时重合点或牵连点。 (3)、注 意
理论力学答案第5章点的复合运动分析
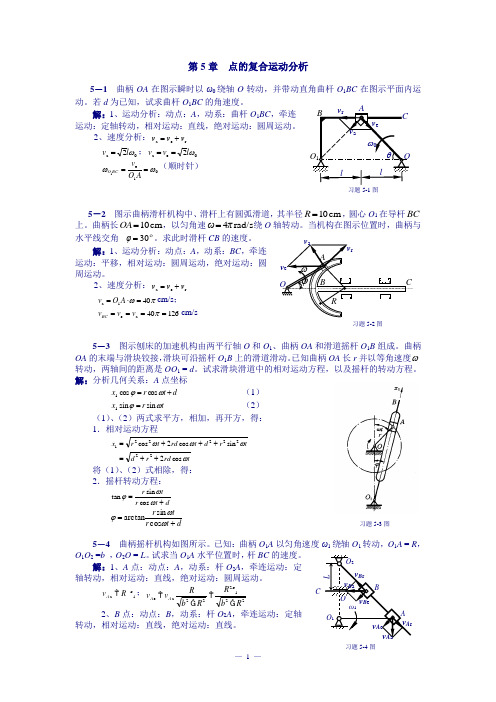
第5章 点的复合运动分析5-1 曲柄OA 在图示瞬时以ω0绕轴O 转动,并带动直角曲杆O 1BC 在图示平面内运动。
若d 为已知,试求曲杆O 1BC 的角速度。
解:1、运动分析:动点:A ,动系:曲杆O 1BC ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
2、速度分析:r e a v v v += 0a 2ωl v =;0e a 2ωl v v == 01e 1ωω==AO v BC O (顺时针)5-2 图示曲柄滑杆机构中、滑杆上有圆弧滑道,其半径cm 10=R ,圆心O 1在导杆BC 上。
曲柄长cm 10=OA ,以匀角速rad/s 4πω=绕O 轴转动。
当机构在图示位置时,曲柄与水平线交角 30=φ。
求此时滑杆CB 的速度。
解:1、运动分析:动点:A ,动系:BC ,牵连运动:平移,相对运动:圆周运动,绝对运动:圆周运动。
2、速度分析:r e a v v v +=πω401a =⋅=A O v cm/s ; 12640a e ====πv v v BC cm/s5-3 图示刨床的加速机构由两平行轴O 和O 1、曲柄OA 和滑道摇杆O 1B 组成。
曲柄OA 的末端与滑块铰接,滑块可沿摇杆O 1B 上的滑道滑动。
已知曲柄OA 长r 并以等角速度ω转动,两轴间的距离是OO 1 = d 。
试求滑块滑道中的相对运动方程,以及摇杆的转动方程。
解:分析几何关系:A 点坐标 d t r x +=ωϕcos cos 1 (1) t r x ωϕsin sin 1= (2) (1)、(2)两式求平方,相加,再开方,得: 1.相对运动方程trd r d t r d t rd t r x ωωωωcos 2sin cos 2cos 22222221++=+++=将(1)、(2)式相除,得: 2.摇杆转动方程: dt r tr +=ωωϕcos sin tandt r t r +=ωωϕcos sin arctan5-4 曲柄摇杆机构如图所示。
第4章 点的复合运动

70
例题
点的复合运动
例 题 3
3. 速度分析。
绝对速度va:va=OA · =r ω ,方 ω 向垂直于OA,沿铅垂
方向向上。
牵连速度ve:ve为所要求的未知量, 方向垂直于O1B 。 相对速度vr:大小未知,方向沿摇杆 O1B 。 应用速度合成定理
l 2 r2
72
r 2 所以可得 1 2 l r2
例题
点的复合运动
例 题 3
讨论:
若取摇杆 O1B上A点为动 点,动系固连 曲柄OA,则相 对运动轨迹是 什么曲线?
73
例题
点的复合运动
例 题 3
讨论:
若取摇杆 O1B上A点为动 点,动系固连 曲柄OA,则相 对运动轨迹是 什么曲线?
55
n
例题
点的复合运动
例 题 1
运 动 演 示
56
例题
点的复合运动
例 题 1 平动实例
相对运动轨迹
57
例题
点的复合运动
例 题 1
解: 1. 选择动点,动系与定系。
B
动点- AB的端点A 。
动系-Ox'y',固连于凸轮。
y'
定系-固连于水平轨道。
A
R φ
v0
2. 运动分析。 绝对运动-直线运动。
得船B的绝对速度和对于船A的相对速度的大小 v v2 1 , v r v1 tan cos 85
ve=v1
va=v2
例题
点的复合运动
解:由坐标变换关系
例 题 7
已知点在平面内运动,
《理论力学》第七章-点的复合运动

v0
Ra
n r
aa
a
φ
x'
O
n
arn
vr2 R
v2
Rsin2
3、速度分析
va vevr
vr
ve
sin
v
sin
4、加速度分析
aaaear arn
n
aasinaecosarn
aa
acot
v2
Rsin3
48
§7–4 牵连运动为转动的加速度合成定理
牵连运动为平动时加速度合成定理:aaaear
牵连运动为定轴平动时 aaaear是否成立?
37
§7–2 速度合成定理
va vr
应用速度合成定理
va vevr
3、速度分析。 绝对速度va: va=OA·ω=rω , 方向垂直于OA向上
牵连速度ve: ve为所要求的未知量,
方向垂直于O1B 相对速度vr: 大小未知, 方向沿摇杆O1B
38
§7–2 速度合成定理
va vr
其中 O1A l2 r2
1
第七章 点的复合运动
§7–1 复合运动的概念 §7–2 速度合成定理 §7–3 牵连运动为平动时点的加速度合成定理 §7–4 牵连运动为转动时点的加速度合成定理
2
第七章 点的复合运动
复合运动问题:研究物体相对于不同参考系 的运动之间的关系。
复合运动不是一种新的运动形式,只是
一种研究运动学问题的思路和方法。
40
§7–3 牵连运动为平动的加速度合成定理
一、绝对运动和相对运动之间的关系
z M
绝对运动方程:r r(t)
z
r (t)
r (t ) k O j
点的复合运动
r 2 l
(l 2 r 2 )1/ 2
1
ae O1 A
r 2 l
l2 r2
2
( l2 r2
1)
1
e
O1 A
r 2
l2 r2
帮助 导航 上一张
下一张
1 ak
aa aen
aet
ar
aa ae aen ar ak
aa r 2 aen O1 A2 1 r 2
ak
21vr
2r3 2l
(l 2 r 2 )3/ 2
aa cos ae ak
ae
ak
aa
cos
2r3 2l
(l 2 r 2 )3/ 2
例题
点的复合运动
例题4
第3章 点的复合运动
§3–2 点的速度合成定理
刨床的急回机构如图所示。曲 柄OA的一端A与滑块用铰链连接。 当曲柄OA以匀角速度ω绕固定轴O 转 动 时 , 滑 块 在 摇 杆 O1B 上 滑 动 , 并带动摇杆O1B绕固定轴O1摆动。 设曲柄长OA=r,两间距离OO1= l。 求当曲柄在水平位置时摇杆的角速
度和角加速度度。
帮助 导航 上一张 下一张
例题
点的复合运动
例题4
y'
x' 第3章 点的复合运动
§3–2 点的速度合成定理
解: 1. 选择动点,动系与定系。
动点-滑块 A 。
动系-O1x'y',固连于摇杆 O1B。
定系-固连于机座。 2. 运动分析。 绝对运动-以O为圆心的圆周运动。 相对运动-沿O1B的直线运动。 牵连运动-摇杆绕O1轴的摆动。
帮助 导航 上一张 下一张
例题
点的复合运动
第八章复合运动

v1
D
v2
K
θ
C E
解: 动点-刀架K
动系-纸板ABCD 绝对运动- 沿导杆的直线运动 相对运动- 牵连运动- 随纸板一起作水平向左的平动
A
F B
v1
D
v2
K
θ
C E va=v2
垂直于纸板的运动方向的直线运动
va ve v r
sin v e v1 0.385 va v2
β
ve
vay´
绝对运动-空间曲线运动
相对运动-以O为圆心的 圆周运动 牵连运动-绕z轴的定轴转动
v x´ r
va ve v r
2 2 2 1
vr= w1R
2 e 2 r
ve= Rw2
va v v R w w
ve w 2 tan vr w1
思考:甲相对于乙的速度为vr, 则能不能直接给出乙 相对于甲的速度? 例 静止的海面上有两艘舰艇A和B,分别以匀速 vA=vB=10(m/s)行驶,如图所示。A艇沿直线向东, B艇则沿以O为圆心, =100m为半径的圆弧行驶。 设在图示瞬时,=30o,s=50(m) 求: (1)B 艇相对于A艇的速度; (2)A 艇相对于B艇的速度。 解
vr 1 v r
ve1 ve '
vr 'vr ve 've v v v v ' e1 e aa lim lim r1 r t 0 t 0 t t va 'va ve1 ve vr 'vr1 lim lim lim t 0 t 0 t 0 t t t
*牵连速度、加速度:ve , ae
牵连点 相对定系的速度、加速度。
点的复合运动1

42
点的速度合成定理
动点在某瞬时的绝对速度等于它在该瞬时的牵连速 度与相对速度的矢量和。
v a ve v r
*矢量方程式,在平面问题中相当两个标量方程式; *建立了任一瞬时三个运动之间的速度关系,不能求
导,只能求得特殊位置(某瞬时)的速度.一定是以绝对
速度为对角线组成平行四边形. *牵连运动形式不限.
动等。
在复合运动的研究中,参考系(动系)的选择是问题的关
键。恰当的选择参考系,能把复杂的运动分解为若干种简
单运动,或由若干种简单运动组成各种不同的复杂运动。
15
5 动点和动系的选择
基本原则:
1.动点对动系要有相对运动。
2.动点的相对运动轨迹要明确、容易确定。 具体选择方法: 1.选择持续接触点为动点。
7
3 三种速度、加速度
*绝对速度、加速度:va , aa
动点相对定系的速度、加速度;
*相对速度、加速度:vr , ar
动点相对动系的速度、加速度; 动点的牵连点:某瞬时动系上与动点重合的点。
*牵连速度、加速度:ve , ae
牵连点 相对定系的速度、加速度。
8
4.牵连点的概念
(1)、定 义 动参考系给动点直接影响的是该动系上与动点相重合的一点,
39
三种运动轨迹
设动点M在动系中沿某一曲线 AB如下
三种运动轨迹
40
刚体在定系中运动,动系固结在刚体上。
M1点——t 瞬时动系上与动点重合的点。 z' x' z M,M1 y x O
41
绝对运动轨迹
M' 相对运动轨迹
y'
r a r r M'1
r e
理论力学---第七章复合运动 (2)

3 2
y
B
ac
l
2w r l
2 3 2 2
r
3
2
wo
ac
aa
ar
A
a a a a a x e x r x c x
a
e
a
n e
x
a cos a a a e c
2 2 rl l r 2 a w 3 e 2 2 2 l r
v ' v v v v ' v a a e 1 e r r 1 l i m l i m l i m t 0 t 0 t 0 t t t
即 M’
vr’ va’ ve’
a a a a r e
M
vr
va vr1 ve M1 t+t ve1
o
t
x
2.牵连运动为转动时的加速度合成定理
应用加速度合成定理 z´
a a a e a r a C
v0
ae aC
x´
M
如以 i , j 和 k 分别表示沿坐标轴 O´x´ , O´y´ 和
O´z´的单位矢量,则M点的加速度aa可表示为
y´
ar
a a a e a r a C
2 2 v v 0 0 R wc o s f j ( c o s f j s i n f k ) 1 1 1 R R 2 w v s i n i 0 1 2
以AD杆上A点为动点,动 系固连于套筒上
例 火车 M 以等速 v0 沿子午线自南往北行驶,如图所示。
为了考虑地球的自转,设定坐标系以地心为原点,坐标轴 分别指向恒星。地球的平均半径为 R 。求火车 M 在北纬 φ 度 处的绝对加速度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.选择持续接触点为动点。
2.对没有持续接触点的问题,一般不选择接触点为动点。 根据选择原则具体问题具体分析。
§7–1 基 本 概 念
练习题1
§7–2 点的速度合成定理
速度合成定理
§7–1 基 本 概 念
三种速度 绝对速度va :动点相对于定系的速度。 相对速度vr :动点相对于动系的速度。 牵连速度ve :动系上与动点相重合的点相对于 定系的速度。
1.两种参考系
物体的运动的描述结果与所选定的参考系有关。同一物体的运动,
在不同的参考系中看来,可以具有极为不同的运动学特征(具有不同的轨 迹、速度、加速度等)。
在实际问题中,往往不仅要知道物体相对地球的运动,而且有时要知 道被观察物体相对于地面运动着的参考系的运动情况。
例如在运动着的飞机、车船上观察其他飞机、车船的运动。 在运动学中,所描述的一切运动都只具有相对的意义。在不同的参考 系中观察到的同一物体的不同运动特征之间存在着一定的联系。
解出未知数。
§7–2 点的速度合成定理 例题7-1
例7-1 军舰以20节(knot,1=1.852 km/h)的速度前进, 直升飞机一每小时18 km的速度垂直降落。求直升飞机相对 于军舰的速度。
例题 7-1
§7–2 点的速度合成定理 例题 7-1
y´
M
O1
解: 1、选择动点与动系
绝对运动: 物体相对于定参考系的运动。 相对运动: 物体相对于动参考系的运动。
牵连运动: 动参考系相对于定参考系的运动。
3. 两种运动轨迹
绝对运动轨迹:动点相对于定系的运动轨迹。 相对运动轨迹:动点相对于动系的运动轨迹。
思考题
§7–1 基 本 概 念
思考题
动 点:滑块上B点。 绝对运动? 动系:固连于曲柄OA。 相对运动? 定系:固连于机座。 牵连运动?
运动学
点的合成运动
第3章 点的复合运动
运动学
第 七
§7–1 基本概念
章
§7–2 点的速度合成定理
点
的
§7–3 牵连运动是平移时点的加
复
速度合成定理
合
§7– 4 牵连运动是定轴转动时点
运
的加速度合成定理
动
目录
§7–1 基本概念
两种参考系 三种运动 牵连点•动点和动系的选择
§7–1 基 本 概 念
在复合运动的研究中,参考系的选择是问题的关键。恰当的选择 参考系,能把复杂的运动分解为若干种简单运动,或由若干种简单 运动组成各种不同的复杂运动。
§7–1 基 本 概 念
4.牵连点的概念
(1)、定 义 动参考系给动点直接影响的是该动系上与动点相重合的一点,
这点称为瞬时重合点或动点的牵连点。
(2)、进一步说明 牵连运动一方面是动系的绝对运动,另一方面对动点来说起
z' M2(m2) y'
x'
vr
M(m)
va
r ve
r1
(1)
M '(m')
r'
M1(m1)
§7–2 点的速度合成定理 va vr ve
绝对速度
相对速度
牵连速度
z' M2(m2) y'
x'
vr
M(m)
va
r ve
r1
M '(m')
r'
M1(m1)
速度合成定理
动点的绝对速度等于其相 对速度与牵连速度的矢量 和。
本章利用运动的分解、合成的方法对点的速度、加速度进行分析,研 究点在不同参考系中的运动,以及它们之间的联系。
§7–1 基 本 概 念
两种参考系
静参考系(定系或静系):在分析问题中,认定不动的参考系。 动参考系(动系):相对于静系运动着的参考系。 一般没特别说明,常以固连于地球的参考系取为静系。
2. 三种运动
A
ω0
B
O
曲柄-滑块机构
思考题
§7–1 基 本 概 念
动 点:杆上A点。
A
动系:固连于滑块B。
定系:固连于墙面。
绝对运动? 相对运动? 牵连运动?
思考题
Bv
§7–1 基 本 概 念
合成运动
由于牵连运动的存在,使物体的绝对运动和相对运动 发生了差别。 如果没有牵连运动,物体的相对运动等同于它的绝对运动。 如果没有相对运动,物体的牵连运动就是它的绝对运动。
由此可见,物体的绝对运动可以看成是牵连运动和相 对运动的合成结果。所以绝对运动也称为复合运动或合成 运动。
§7–1 基 本 概 念
几点说明
本章只研究点的复合运动理论,通过牵连运动来建立绝对运动和相 对运动之间的联系,给出这些运动特征量(轨迹、速度、加速度)之 间的关系。
必须指出在这一章,绝对运动、相对运动都是指点的运动,可能是 直线运动,也可能是曲线运动;而牵连运动是指刚体的运动,可能是 平动、定轴转动或下一章的平面运动等。
MM MM1 M1M
则有
分析其中各项
lim
t 0
MM t
va
lim MM lim MM1 lim M1M
t0 t
t0 t
t0 t
lim MM1 t0 t
lim mm1 t0 t
vm
ve
lim M1M lim MM 2
t0 t
t0 t
vr
代入(1)式可得
va vr ve
着“牵连”作用。但是带动动点运动的只是动系上在所考察的瞬 时与动点相重合的那一点,该点称为瞬时重合点或牵连点。 (3)、注 意
由于相对运动,动点在动系上的位置随时间改变,所以牵连点
具有瞬时性。
§7–1 基 本 概 念
牵连点
复ቤተ መጻሕፍቲ ባይዱ运动实例
牵连点
§7–1 基 本 概 念
5、 动点和动系的选择
基本原则: 1.动点对动系要有相对运动(动点动系不能位于同一物体上)。 2.动点的相对运动轨迹要明确、容易确定。
§7–2 点的速度合成定理
三种运动轨迹
设动点M在动系中沿某一曲线AB作相对运动,而动系本身相对定
系作某种运动,相应的运动轨迹如下
z' M2(m2) 绝对运动轨迹 y'
x'
M'(m')
相对运动轨迹
z xO
M (m) y
M1(m1)
牵连点运动轨迹
§7–2 点的速度合成定理
速度合成定理
动点M在时间△t 内的绝对位移
§7–2 点的速度合成定理
va vr ve
几点说明
牵连运动是指刚体(动系)的运动;而牵连速度是指刚体
上一点(与动点相重合的点)的速度。
速度合成定理为平面矢量方程,由此可以写出两个投
影式,所以可以求解两个未知量。
速度合成定理对任意形式的牵连运动都适用。
解 (1)选定动点、动参考系和定参考系。 题 (2)分析三种运动和三种速度。 步 (3)作出速度平行四边形。 骤 (4)利用速度平行四边形中的几何关系
