第5章点的复合运动
理论力学-5-运动学基础

ds =v =s dt
dv at s dt
an
v
2
a a a
2 τ
2 n
5.1 点的运动学
自然轴系
自然轴系
当运动轨迹为空间曲线时,弧坐标系中所得 到的结论同样成立,只需将弧坐标系扩展为自然 轴系。
5.1 点的运动学
自然轴系P-TNB
B(副法线) N(主法线)
0
dτ n d
5.1 点的运动学
τ vτ av
τ
弧坐标法
τ ?
ds =v =s dt
dτ dτ d ds dt d ds dt
dτ n d
d 1 曲率 ds
a at an at τ an n
速度方向的变化率 法向加速度
xA OC CM R
M
即
CM v0t R R
v0t x OC AM sin v t R sin 0 R 于是M点的运动方程为: vt y AC AM cos R R cos 0 R
5.1 点的运动学
v0t x OC AM sin v t R sin 0 R vt y AC AM cos R R cos 0 R
切线方向的单位矢量为t ,则有 r ds lim τ =v = s t 0 s dt t指向弧坐标s增加的方向。 动点的速度为
τ v vτ s
速度方向
速度大小
5.1 点的运动学
弧坐标法
加速度
dτ dτ d ds dt d ds dt dτ d 1 ds 曲率 ? =v =s ds d dt τ
理论力学答案第5章点的复合运动分析
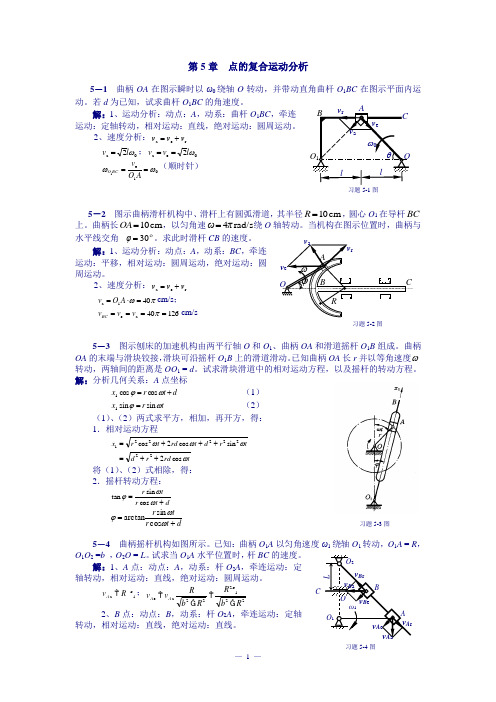
第5章 点的复合运动分析5-1 曲柄OA 在图示瞬时以ω0绕轴O 转动,并带动直角曲杆O 1BC 在图示平面内运动。
若d 为已知,试求曲杆O 1BC 的角速度。
解:1、运动分析:动点:A ,动系:曲杆O 1BC ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
2、速度分析:r e a v v v += 0a 2ωl v =;0e a 2ωl v v == 01e 1ωω==AO v BC O (顺时针)5-2 图示曲柄滑杆机构中、滑杆上有圆弧滑道,其半径cm 10=R ,圆心O 1在导杆BC 上。
曲柄长cm 10=OA ,以匀角速rad/s 4πω=绕O 轴转动。
当机构在图示位置时,曲柄与水平线交角 30=φ。
求此时滑杆CB 的速度。
解:1、运动分析:动点:A ,动系:BC ,牵连运动:平移,相对运动:圆周运动,绝对运动:圆周运动。
2、速度分析:r e a v v v +=πω401a =⋅=A O v cm/s ; 12640a e ====πv v v BC cm/s5-3 图示刨床的加速机构由两平行轴O 和O 1、曲柄OA 和滑道摇杆O 1B 组成。
曲柄OA 的末端与滑块铰接,滑块可沿摇杆O 1B 上的滑道滑动。
已知曲柄OA 长r 并以等角速度ω转动,两轴间的距离是OO 1 = d 。
试求滑块滑道中的相对运动方程,以及摇杆的转动方程。
解:分析几何关系:A 点坐标 d t r x +=ωϕcos cos 1 (1) t r x ωϕsin sin 1= (2) (1)、(2)两式求平方,相加,再开方,得: 1.相对运动方程trd r d t r d t rd t r x ωωωωcos 2sin cos 2cos 22222221++=+++=将(1)、(2)式相除,得: 2.摇杆转动方程: dt r tr +=ωωϕcos sin tandt r t r +=ωωϕcos sin arctan5-4 曲柄摇杆机构如图所示。
第五章机构的组成及平面连杆机构

2
1
4
3
5
E
F
未去掉虚约束时
2 1
3
E 5
F 4
F3n2pLpH34260 ?
附加的构件5和其两端的转动副E、F提供的自由度
F3122 1 即引入了一个约束,但这个约束对机构的运动不起实际 约束作用,为虚约束。去掉虚约束后
F3n2pLpH33241
⑶ 联接构件与被联接构件上联接点的轨迹重合
B2
E
C
第五章 机构的组成及平面连杆
机构
平面机构运动简图 自由度 铰链四杆机构的基本形式 平面连杆机构曲面存在的条件 急回特性 死点 平面连杆机构的设计 三心定理及应用 平面机构的组成原理及结构分析
组成机构的所有构件都在一个或几个相 互平行平面中运动的机构称平面机构,否 则称空间机构。工程中常见的机构一般都 是平面机构。
31
2
4
1 2
3
1
2 3
两个转动副
4
两个转动副
两个转动副
平面机构自由度计算(4)
构件2、3、4在铰链 C处构成复合铰链, 组成两个同轴回转副 而不是一个回转副, 所以,总的回转副数 是PL=7,而不是PL=6,
F 35 27 0 1
(2) 局部自由度
定义:
不影响整个机构运动的局部独立运动。 对整个机构其他构件运动无关的自由度。
D4 E
B3
1
2
5 F
6
7 G
8 K 9
A C
H
I
局部自由度
D4 E
B3
1
2
5 F
6
7 G
A C
H
I
复合铰链
《电机与电气控制》课件第5章

5.2.4
生产实践中,很多设备需要两个相反的运行方向,例如 工作台的前进和后退,起重机吊钩的上升和下降等,这些应 用中两个相反方向的运动均可通过电动机的正转和反转来实 现。对于交流电动机,改变电动机定子绕组相序即可改变其 转动方向。在主电路中,通过两组接触器主触点构成正转相 序接线和反转相序接线,从而实现电动机的正、反转控制。
5.1 电气控制图的绘制规则和常用符号
5.1.1
电气控制系统是由许多电气元件按一定要求连接而成的。 为了表达机械电气控制系统的结构、工作原理,同时也为了 便于电气元件的安装、接线、运行、维护,将电气控制系统 中各电气元件的连接用一定的图形表示出来,这种图就是电
按用途和表达方式的不同,电气图可分为以下几种。
3. 图5-1所示的某机床电控系统线路图中,三相交流电源 引入线用L 1、L 2、L 3标记,中性线用N标记,保护 接地用PE标记。
图5-1 某机床电控系统线路图
电源开关之后的三相交流电源主电路分别按U、V、W 顺序标记。分级三相交流电源主电路采用U1、V1、W1、U2、 V2、W2
各电动机分支电路中各接点采用三相文字代号后面加数 字来表示,数字中的十位数表示电动机代号,个位数表示该 支路各接点的代号,从上到下按数值大小顺序标记,如 “U21”表示M2
5. 电气元件明细表是把成套装置以及设备中各组成元件 (包括电动机)的名称、型号、规格和数量等列成的表格,供
以上简要介绍了电气图的分类,不同的图有不同的应用 场合。本书主要介绍电气原理图的分析和理解。
5.1.2
电气图是电气技术人员统一使用的工程语言。电气图应 根据国家标准,用规定的图形符号、文字符号以及规定的画
理论力学点的合成运动

例 8-4 曲柄OA以匀角速度 w绕O轴转动,其上
套有小环 M,而小环 M又在固定的大圆环上运动,大 圆环的半径为 R。
试求当曲柄与水平线成的角 j ωt 时,小环 M
的绝对速度和相对曲柄 OA 的相对速度。
A
M w
R
O
j
C
解:(1)选择动点及 动系: 小环M为动点,动系固连在 OA上。
(2)分析三种运动:绝 对运动为圆周运动,相对运 动为沿OA的直线运动,牵连 运动为定轴转动。
y
OA杆转动的角速度为
O
wOA
ve OC
ve 2r
3u 6r
y
wOA B
j va vr
A
r ve C
x
u x
8.3 牵连运动是平动时点的加速度合成定理
在图8-9中,设 Oxyz为定系,Oxyz为动系且作平
动,M为动点。动点M在动系中的坐标为 x、y 、z, 动系单位矢量为 i、 j、k。动系平动,i、j、k 的
Oxyz 作某种运动,在瞬时t,动系连同相对轨迹AB在
定系中的I位置,动点则在曲线 AB
上的 M 点。经过时间间 隔 t ,动系运动到定系 中的II位置,动点运动到
点 M。 如果在动系上观
察点M 的运动,则它沿 曲线 AB 运动到点 M2。
z B
M2
vr
z
M O
A
O I
x
va
M B
ve M1
z
O x A
例 8-1 汽车以速度 v1 沿直线的道路行驶,雨滴 以速度 v2 铅直下落,试求雨滴相对于汽车的速度。
v1
解: 因为雨滴相对运动的汽车有运动,所以本题 为点的合成运动问题,可应用点的速度合成定理求解。
点的合成运动

r '
M1(m1)
§8−2 点的速度合成定理
va vr ve
绝对速度 相对速度
M '(m')
牵连速度
z' x'
M2(m2)
速度合成定理 动点的绝对速度等于其相 对速度与牵连速度的矢量 和。
y'
va
r
vr
M(m)
ve r 1
r '
M1(m1)
§8−2 点的速度合成定理
va vr ve
§8−1 合成运动基本概念 合成 本概
动点-摇杆上 A'点。 动系-固连于
'
曲柄OA。
§8−1 合成 合成运动基本概念 本概 练习题 4
动点-滑块 动点 滑块 A 。 动系-固连于 T形槽杆BAC。
§8−1 合成运动基本概念 合成 本概
动点- T形槽 杆上 A'点。 动系-固连于 曲柄OA。
§8−1 合成运动基本概念 合成 本概
试比较其共同点
§8−1 合成运动基本概念 合成 本概
试比较其共同点
§8−1 合成 合成运动基本概念 本概 4. 相对运动 相对运动方程 r r (t )
x x(t )
y y (t )
z z (t )
s s(t )
M
§8−2 点的速度合成定理
y'
解: (1) 运动分析 动点-滑块 M 。
M
动系- Ax'y'固连于摇杆 AB。 定系-固连于机座。 绝对运动-以O为圆心的圆周运动。
x'
相对运动-沿AB的直线运动。 牵连运动-摇杆绕A轴的摆动。
§8−2 点的速度合成定理
《理论力学》(范钦珊)习题解答第2篇第46章.doc

(b)第2篇 工程运动学基础第4章 运动分析基础4-1 小环A 套在光滑的钢丝圈上运动,钢丝圈半径为R (如图所示)。
已知小环的初速度为v 0,并且在运动过程中小环的速度和加速度成定角θ,且 0 < θ <2π,试确定小环 A的运动规律。
解:Rv a a 2ns in ==θ,θs in 2R v a =θθt an co s d d 2tR v a tv a ===,⎰⎰=t v v t R v v 02d t an 1d 0θ t v R R v t s v 00t an t an d d -==θθ⎰⎰-=t s t t v R R v s 0000d tan tan d θθtv R R R s 0t an t an ln tan -=θθθ4-2 已知运动方程如下,试画出轨迹曲线、不同瞬时点的 1.⎪⎩⎪⎨⎧-=-=225.1324t t y tt x , 2.⎩⎨⎧==t y t x 2cos 2sin 3解:1.由已知得 3x = 4y (1) ⎩⎨⎧-=-=t y t x3344 t v 55-=⎩⎨⎧-=-=34y x5-=a 为匀减速直线运动,轨迹如图(a ),其v 、a 图像从略。
2.由已知,得2ar cco s 213ar cs i n y x =化简得轨迹方程:2942x y -=(2)轨迹如图(b ),其v 、a 图像从略。
4-3 点作圆周运动,孤坐标的原点在O 点,顺钟向为孤坐标的正方向,运动方程为221Rt s π=,式中s 以厘米计,t 以秒计。
轨迹图形和直角坐标的关系如右图所示。
当点第一次到达y 坐标值最大的位置时,求点的加速度在x 和y 轴上的投影。
解:Rt s v π== ,R v a π== t,222n Rt Rv a π==y 坐标值最大的位置时:R Rt s 2212ππ== ,12=∴tR a a x π==t ,R a y 2π-=4-4 滑块A ,用绳索牵引沿水平导轨滑动,绳的另一端绕在半径为r 的鼓轮上,鼓轮A习题4-1图习题4-2图习题4-3图e e -t (c)e e -t υ (b)R t R +υ (a)习题4-6图以匀角速度ω转动,如图所示。
点的合成运动

2013年7月5日
理论力学CAI
42
1.牵连运动为转动时点的加速度合成定理
设一圆盘以匀角速度 绕 定轴O顺时针转动,盘上圆槽 内有一点M以大小不变的速度 vr 沿槽作圆周运动,那么M点
相对于定系的绝对加速度应是
多少呢?
2013年7月5日
理论力学CAI
43
选点M为动点,动系固结于圆盘上,
则M点的牵连运动为匀速转动, 为常数
y'
y u
x'
M
O
M O
y'
x'
x
O'
2013年7月5日
理论力学CAI
4
车刀以匀速横向走刀,卡盘匀角速度转动,求刀尖相对工件的轨迹。
2013年7月5日
理论力学CAI
5
§8-1 相对运动、牵连运动、绝对运动
归纳为:一点,两系,三种运动
一点
动点:做合成运动的点。
两系
定参考系(定系):固结于地面(地球)。如机座。 动参考系(动系):固结于某运动着的刚体上。
ar = 2l sin
理论力学CAI
37
课后作业1(浙大)
作业题 7-7 7-8 7-9
2013年7月5日
理论力学CAI
38
课后作业1
思考题 8-1 8-2 作业题 8-7 8-8
8-3
8-10
2013年7月5日
理论力学CAI
39
例题
例 曲柄滑杆机构
= 45o 时,, a ; 已知: OA=l ,
例题
已知:AB匀角速度转动。 求:M在导槽EF及BC中运动的速度与加速度。
E
B
C M
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
点的速度合成定理是矢量式,有两个投影方程,可求解 2 个未知量,3 个速度矢量共 6 个量(大小 方向) ,若知道其中任 意 4 个量,即求出其余两个量。 (2)矢量证明
v e vo' rr
va ve vr
(1 )当牵连运动为平动 0 ,动系上各点速度相同,故
v e v o'
是不同的(动系作平动除外) ,在同一瞬时,动系上与动点位置 相重合的点称为牵连点,含有牵连点的动系相对于定系的运动即 为牵连运动。 (为平动或转动或复杂运动的动系相对于定系的运 动 注:绝对运动是相对运动和牵连运动的合成。 4、动系、动点的选取原则: (1)动点、动系和静系必须分别选在三个物体上。静系一 般固定在地面或与地固连的机架上,即静系固定在不动的物体 上。 (2)动点和动系不能选在同一个运动的刚体上,若选在同一 个刚体上,动点对动系就不会有相对运动。 (3)动点相对动系的相对运动轨迹简单、明显,如相对轨迹 是直线,圆等。 (4)动系的运动要容易判定,如平动和转动等。 (5)对于有约束联系的系统,例如机构转动问题,动点多选 取主动件与从动件的连接点,并与其中一个构件固接,而动系固 定在另一运动的构件上。 (6)对于没有约束联系的系统,所研究的点为动点,如雨滴, 矿砂,物料:动系固定在另一运动的物体上,如车辆,转送带, 四、三种速度 绝对速度 相对速度 牵连速度 1、绝对速度: 动点相对于定系运动的速度 2、相对速度: 动点相对于动系运动的速度。
图 5-2 车轮轮缘上点 M 的复合运
实例之二: 研究沿地面作直线滚动的车轮轮缘上点 M 的运动 (1)静系中:动点的轨迹是旋轮线车厢作直线运动
(2)动系中:M 动点作圆周运动 (3)运动的同时性,M 点运动和平动是同时进行的,M 点 既跟随着动系一起平动,又在动系上作圆周运动。旋轮线就是这 两个运动的合成运动的轨迹, 轮缘上 M 点的运动就是这两个简单 运动的合成。 实例 3: 在大梁固定不动时, 卷杨小车沿大梁可作直线运动, 同时将吊钩上的重物 A 铅垂向上提升, 研究重物的运动称合成运 动 (1)静系中:A→B (2)动系中:A →A’ (3)同时性: 点:A →A’ 小车:A→B 重物既跟随动系一起向右平动, 图 5-3 吊重物的复合
3、牵连速度: 牵连点相对于动系运动的速度 动坐标系是一个包含与之固连的刚体在内的运动空间,除动 坐标系作平移外,动坐标系上各点的运动状态是不相同的。在任 意瞬时,只有牵连点的运动能够给动点以直接的影响。为此,定 义某瞬时,与动点相重合的动坐标系上的点(牵连点)相对于静 坐标系运动的速度称为动点的牵连速度。动点和牵连点是一对相 伴点。 例如,直管 OB 以匀角速 度绕定轴 O 转动,小球 M 以 速度 u 在直管 OB 中作相对的 匀速直线运动, 如图示。 将动坐 标系固结在 OB 管上,以小球
C→D。
(3)同时性:先假设河水不动,则小船从 A 划到 B :在假 设人不划船,小船随河水漂流到下游 D 处。实际上小船和水是同 时运动的,小船动点的运动是上述两个简单运动的合成
v y A x v y' x' C vr ve va D vr M O B va ve x y y' O ' x'
图 5-1 小船的复合运动 动
(2)当牵连运动为定轴转动, v o' 0 ,故 v e rr 。 三、运用点的速度合成定理解题的方法步1)凡速度大小可以算出的求出其值,凡方向已知的画出 其方向。 (2)作速度平行四边形求解未知量,v a 是 v e、v r 为邻边的对
C 点的平行的无限大的平板
(2)运动分析:牵连运动为平板的平动,而动系平动,其 上各点的速度是相同的。 v e vC 即牵连点随板平动。 (3)速度平行四边形
e2 ( 3e) 2 2 3e0 ve va =e cos 3 3e
讨论:动系不同 v e、v r 则不同,但 v a 不变。
rr ──相对矢径,相对运动方程,相对轨迹。
z
y
z
M
'
y'
'
y'
x'
y
M y'
'
r r ra k
x O
O
x'
yO' y O
x'
φ
O
r'
O
x xO' x
i
j
图 5-5 矢径表示
图 5-6 直角坐标表示
二、用直角坐标表示运动方程。
' x xO x' cos - y' sin ' y yO x' sin y' cos
在点的绝对运动方程中消去时间 t,即得点的绝对运动轨迹;在 点的相对运动方程中消去时间 t,即得点的相对运动轨迹。 例如清华《教材》P.97 例 5-1。
5.3 复合运动中速度之间的关系 一、解析法求速度 将三种运动方程之间的关系式对时间连续求导,可得三种 运动中速度之间与加速度之间的关系,这就是求解点的复合运动 的解析法。 例如清华《教材》P.98 例 5-2。 二、速度合成定理 1、绝对速度应是相对速度和牵连速度合成的矢量。
va ve = v 1c tan tan
例 5-2:有常接触点: 已知:θ、u 水平向右。DE 杆沿滑 槽上下运动,求 DE 杆的速度。
E
B
y'
x'
D
θ
u
A
vr
va
ve
θ
图 5-9 有常接触点的运动分析之一 〈1〉 运动分析: 从动杆下端 D 为常接触点, 取其为动点,
动点的绝对运动为铅垂向上的直线运动,相对运动为沿斜面向上 的直线运动,牵连运动为尖辟的平动。 〈2〉 〈3〉 速度分析:速度平行四边形见图。 求 DE 杆的速度:
va ve vr
2、推导: (1)几何证明:
图 5-7 速度合成定理
动点在一个任意运动的刚体 K 上沿弧 AB 相对于刚体 K 运 动,动坐标系固结刚体 K 上,静坐标系固结在地面上。 瞬时 t,动点位于 M 处,t 后动点运动到 M 1‘ 处。绝对运动
‘ 轨迹 MM 1 ,M1 是瞬时 t 的牵连点, MM 1 是此牵连点的轨迹。 MM1 MM1 M1 M1 MM1 MM1 M1 M1 lim lim lim t 0 t 0 t t 0 t t MM1 MM1 M M v a lim v e lim v r lim 1 1 t 0 t t 0 t t 0 t va ve vr
第 5 章 点的复合运动 5.1 复合运动中的基本概念 5.2 复合运动中的运动方程之间的关系 5.3 复合运动中的速度之间的关系 一、目的要求: 1、使学生了解速度和加速度的矢量式 2、理解绝对运动,相对运动和牵连运动 3、使学生对合成运动问题能恰当地选择动点,动系和定系, 并能较正确的判定点的绝对,相对和牵连运动 4、使学生掌握速度合成定理,并能较正确应用它解点的速 度合成运动问题。 二、重点:绝对运动,相对运动和牵连运动的概念,速度合 成定理及其应用。 难点:牵连运动,牵连点,动点,动系的选择 三、学时安排:4 学时 四、教学准备:幻灯片 五、教学过程 导入新课: 5.1 复合运动中的基本概念 一、 概念: 1、静参考系:固定在地球上的坐标。
A1 的运动为绝对运动,其速度为 v a 。
5.2 复合运动中的运动方程之间的关系 一、 用矢径表示的运动方程 1、Oxyz: ra ra (t ) xi + yj + zk
ra ──绝对矢径。是动点矢量形式的绝对运动方程;其矢端
曲线就是动点的绝对轨迹。 2、O’x’y’z’: rr rr (t ) x ' i + y'j + z'k
M 为动点。 随着动点 M 的运动,
牵连点在动坐标系中的位置在
图 5-4 牵连点 牵连速度
相应改变。设小球在 t1、t2 瞬时分别到达 M1、M2 位置,则 动点的牵连速度分别为
v e1 OM 1 v e 2 OM 2
五、实例简述三种运动. 三种速度 1、小船过河 (1)动系、定系、动点分别在河水上、河岸上、小船。 (2)运动分析:小船(从 A→ B)相对于河水的运动是相 对运动,其速度为相对速度 v r ,小船随河水的漂动(即从 A→ C)
例 5-4: 有常接触点 已知:曲柄 OA 以 r、 ,匀速转动。带动摇杆的转动。 求:当 30 摇杆的角速度 1
r O1
B
y O1
r
B A
ω
x'
ω
A
ve
vr va
ω1 ω1
θ
y
'
θ
O2
(a)
O2
(b)
x
图 5-11 有常接触点的运动分析之三 分析: (1)三选:取曲柄 OA 的端点 A(即滑块 A)常接 触点为动点。机座上固连定系 Oxy 摆杆 OB 上固连动系 Ox’y’。 (2)运动分析:滑块 A 的绝对运动是以 O 为圆心,r 为半 径的圆周运动:动点的相对运动为沿 OB 的直线运动;牵连运动 为摆杆的定轴转动(绕 O2)即牵连点随动系的转动 (3)速度分析:作速度平行四边形, v e 为动系上的牵连点 的速度
运动又在动系上从下往向运动,重物的运动是两个简单运动的合 成。 三. 三种运动 绝对 相对 牵连
1、绝对运动:动点相对于静系的运动,即人站在地面上观 察点的真实运动。 2、相对运动:动点相对于动系的运动,即人站在动系上(或 人站在运动的物体上)观察点的运动。 3、牵连运动:动点随动系相对于静系的运动,即人站在地 面上观察动点随动系的运动。由于动系上各个点的运动速度一般
