磁场对载流导线的作用力安培力磁场对载流线圈的作用力矩
合集下载
磁场对载流导线产生的力与力矩
磁场对载流导线产生的力与力矩导线通过电流时会在其周围产生磁场，而磁场又会对导线产生力与力矩的作用。
这是一种非常有趣的物理现象，对于我们理解电磁学和应用于电路中的原理至关重要。
首先，我们来讨论磁场对载流导线产生的力。
根据安培力定律，当导线通过磁场时，磁场会对导线中的电流产生作用力。
这个力的大小与磁场的强度、导线中的电流以及导线与磁场的夹角有关。
为了理解这一点，我们可以想象一个简单的实验。
构建一个导线回路，将其置于磁场中，并通过导线通电。
我们会观察到导线会受到磁场的作用力，并在垂直于磁场方向上受力。
当导线垂直于磁场时，力的大小最大；而当导线与磁场平行时，力的大小为零。
这与安培力定律的描述一致。
在实际应用中，这种力的作用可以被用于各种有用的设备和系统中。
例如，我们可以利用这一原理制造电动机、发电机和磁悬浮列车等。
通过调整导线的位置和方向，可以控制力的大小和方向，从而实现各种功能。
接下来，我们来讨论磁场对载流导线产生的力矩。
力矩是一个物体受力作用后产生的旋转效应。
在磁场中，导线所受力的作用点可能不在导线的中心，导致了力矩的产生。
当电流通过导线时，每一段导线上的电荷会感受到磁场的力。
由于导线上的电荷分布不均匀，所以力的作用点也会不均匀。
导致导线在磁场中受到一个力矩的作用。
这个力矩与导线上的电流、磁场的强度以及导线的几何形状等因素有关。
如果我们将导线连接到一个可转动的轴上，就可以观察到这个力矩的旋转效应。
当导线中的电流通过时，力矩会导致导线围绕轴旋转。
这种现象在电动机和电磁铁等设备中广泛应用。
对于理解磁场对载流导线产生的力与力矩，我们还需要考虑右手法则。
右手法则是一种简单的工具，可以帮助我们确定力和力矩的方向。
在磁场中，我们可以用右手的大拇指、食指和中指来表示磁场，电流和力的方向。
通过掌握右手法则，我们可以更准确地预测和控制磁场对载流导线的作用。
这对于设计和优化电路和电磁设备非常重要。
总结起来，磁场对载流导线产生的力与力矩是电磁学中非常重要的原理。
大学物理 磁场对载流导线的作用..
M BIS sin
而M的作用是使减少，所以磁力矩的功为负值，即
dW Md BIS sin d
BISd( cos ) Id(BS cos ) Id
12
线圈从11 ) I
Pm ISn I
2
Rn
2
在图示位置时，线圈磁矩Pm的方向与B垂直.
14
线圈所受磁力矩大小为
1 M Pm B sin IBR 2 2 2
磁力矩 M 的方向由 P 确定，垂直于 B 的方向向上. m B (2)计算磁力矩做功.
1 1 2 A I I ( 2 1 ) I ( B R 0) IB R 2 2 2
9
讨 论
M Pm B
2）方向相同 稳定平衡
+ + +
P m 方向与 B 垂直 1）
力矩最大 I
3）方向相反
非稳定平衡
+
F
‘ '
F
.
B
, M NBIS 2
. I . . ' + + + + + + F F . . . ' + F + + + + F+ . . . B
+ + + + + +
I
+ +
.
.
.
. . .
. . .
.B .
0 ,M 0
,M 0
10
四、磁力的功 1.载流导线在磁场中运动时磁力所做的功 如图，ab长为l，电流I，ab边受力 方向向右。 d
磁场 对载流导线的作用
dN
个电子通过导线界面时间为
dt，根据电流的定义
I
dq dt
(dN )e dt
，得
Idl
(dN )e dt
dl
(dN )e
dl dt
(dN )ev
因为电流的方向与电子的运动方向相反，即 Idl (dN)ev
将上式带入 dF 的表达式，可得电流元所受的磁力为 dF Idl B
磁场对电流元的作用力等于电流元与电流元所在处磁感应强度的矢积。这一规律首先是由安培在实 验中得到的，故称为安培定律。载流导线在磁场中受到的力称为安培力。
定义载流线圈磁矩 m 的大小为 m NIS
取 m 的方向与线圈平面的法向一致。
若用 en 表示线圈法向的单位矢量，遵循右手螺旋法则，则载流线圈的磁矩为 m NISen
由此得到载流线圈所受的磁力矩大小为 M mBsin
用矢量表示为 M m B ，磁力矩的方向与 m B 的方向一致。
磁场对载流导线的作用 1.2 磁力矩
【解】 在载流导线上任取一电流元 Idl，该电流元所受的安培力大小为 dF IBsin dl IBdl 该力 2
的方向沿矢径向斜向上。由于对称性，半圆上各电流元受到的安培力沿 x 轴的分量相互抵消，所以整个
半圆弧所受的合力方向竖直向上。 F Fy =
/2
/2
IBsindl 2 IBRsind 2IBR sind 2IBR
L
0
0
整个弯曲导线所受的安培力可等效为从起点到终点连成的直导线通过相同的电流时所受的安培力。
可以证明，此结论对匀强磁场中的任意形状载流导线均成立。
磁场对载流导线的作用
1.2 磁力矩
如图所示，在磁感应强度为 B 的匀强磁场中，有一刚性矩形线圈 ABCDA，其边长为 l1 和 l2 ，通 有电流 I。设线圈平面的法向矢量 en （ en 的方向与电流的流向遵循右手螺旋关系）与磁感应强度 B 之间的夹角为 。
第4次 安培定律
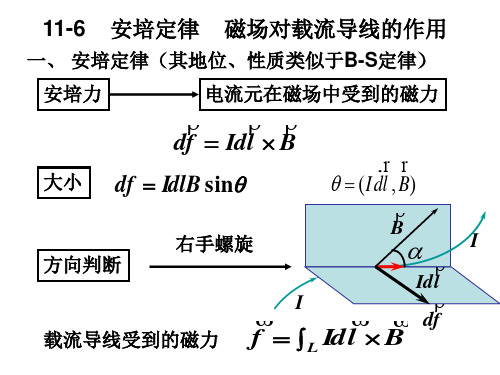
M
θ
Pm
B
A = ∫ Id Φ m
例
一半径为R的半圆形闭合线圈，通有电流 ， 一半径为 的半圆形闭合线圈，通有电流I，线 的半圆形闭合线圈 圈放在均匀外磁场B中 的方向与线圈平面成30 圈放在均匀外磁场 中，B的方向与线圈平面成 0 的方向与线圈平面成 如右图，设线圈有N匝 角，如右图，设线圈有 匝，问：
11-7 磁场对载流线圈的作用 l 2
F1 l1
a
l2
⊙
d B
⊗
d
F2
•
′
I
F2
n c
′
F2 θ
′
l1
×
B
θ
d (c ) θ
a (b )
n
F2
b F1
′
Pm
F2 = F2 = BIl 2
d = l1 sin θ
Pm = ISn
M = Fd = BIl 2 l1 sin θ = B IS sin θ = BPm sin θ
f =0
I
B
fmax = BLI
I
2、任意形状导线 、 取电流元
Idl
受力大小 df = BIdl 方向如图所示 建坐标系取分量
y × × × df Idl × × × α O × × ×
B × × × × × ×
x
b
a
df x = df sin α = BIdl sin α = BIdy df y = df cos α = BIdl cos α = BIdx
可见， 可见，磁力矩作正功
W = NI ∆Φ m = NI ( Φ 2 m − Φ1m )
11-5 带电粒子在电场、磁场中运动 洛伦兹力 带电粒子在电场、 一 带电粒子在电场和磁场中所受的力 电场力 Fe = qE 磁场力（洛伦兹力） 磁场力（洛伦兹力）
磁场的作用力
磁场对载流导线的作用
一、 安培定律
1. 磁场对电流元的作用
安培力：
dF
Idl
B
安培定律
大小 dF IdlBsin
I
arcsin( Idl ,B )
方向判断： 右手螺旋
r
Idl
B
dF
2. 载流导线所受磁场力
F L dF L Idl B
均匀磁场中载流直导线所受安培力
例 计算长为 L 的载流直导线在均匀磁场 B中所受的力。
由于等离子体温度太高必须使用磁约束装置来充当容器
带电粒子的速度v和磁感强度B成 任意夹角时，此带电粒子在磁场 中作螺旋线运动，且回旋半径R 与磁感强度B成反比，磁场越强， 半径越小，这样一来，在很强的 磁场中，每个带电粒子的运动便 被约束在一根磁感线附近的很小 的范围内
两个电流方向相同的 线圈产生中央弱两端 强的不均匀磁场
2
d
三、磁场对载流线圈的作用
设均匀磁场，矩形线圈
F1
F1
BIl1
sin( 2
)
BIl1 cos
F1 F1 且在同一直线上
F2
F2
BIl 2
sin 2
BIl 2
F2 F2 但不在同一直线上
整个线圈 F 0
F1 l1 d
a
2
IB
l2 b
c F1' n
a(b)
F2
F2'
d(c)
n
B
还用于继电器、电机、以及各种高频电磁元件 的磁芯、磁棒。
(2)硬磁材料——作永久磁铁 钨钢，碳钢，铝镍钴合金
B
HC
HC H
矫顽力(Hc)大（>102A/m)，剩磁Br大 磁滞回线的面积大，损耗大。
一、 安培定律
1. 磁场对电流元的作用
安培力：
dF
Idl
B
安培定律
大小 dF IdlBsin
I
arcsin( Idl ,B )
方向判断： 右手螺旋
r
Idl
B
dF
2. 载流导线所受磁场力
F L dF L Idl B
均匀磁场中载流直导线所受安培力
例 计算长为 L 的载流直导线在均匀磁场 B中所受的力。
由于等离子体温度太高必须使用磁约束装置来充当容器
带电粒子的速度v和磁感强度B成 任意夹角时，此带电粒子在磁场 中作螺旋线运动，且回旋半径R 与磁感强度B成反比，磁场越强， 半径越小，这样一来，在很强的 磁场中，每个带电粒子的运动便 被约束在一根磁感线附近的很小 的范围内
两个电流方向相同的 线圈产生中央弱两端 强的不均匀磁场
2
d
三、磁场对载流线圈的作用
设均匀磁场，矩形线圈
F1
F1
BIl1
sin( 2
)
BIl1 cos
F1 F1 且在同一直线上
F2
F2
BIl 2
sin 2
BIl 2
F2 F2 但不在同一直线上
整个线圈 F 0
F1 l1 d
a
2
IB
l2 b
c F1' n
a(b)
F2
F2'
d(c)
n
B
还用于继电器、电机、以及各种高频电磁元件 的磁芯、磁棒。
(2)硬磁材料——作永久磁铁 钨钢，碳钢，铝镍钴合金
B
HC
HC H
矫顽力(Hc)大（>102A/m)，剩磁Br大 磁滞回线的面积大，损耗大。
07-02 安培定律
l1
a
l2 I
b
a,b
F
B
c
en
F
c,d
B
en
7－2安培定律及其应用
载流线圈的磁距: m I S
N
则磁力矩为: M m B
7－2安培定律及其应用
讨论
1）en方向与 B 垂直 2）方向相同
3）方向相反
力矩最大
稳定平衡
不稳定平衡
I
F.
F
B
π 2
,M
M max
++++++
I
++++++
+ F+ + + + +
方向：
dF I1dl B I1dx B
x
al
F dF
l
a
BI1dx
al a
0 I 2 2 x
I1dx
0I1I2 ln a l 2 a
7－2安培定律及其应用 结论
{ （ab B
即整个弯导线可由连接两端而成的直导线等效。
结论：在均匀外磁场中，任意曲导线的受力与 头尾相连的直导线受力一致。
B
I
o
L
I
b
a
c
d
L
P
F=BI(L+2R) 方向:竖直向上
7－2安培定律及其应用
例2：在一长直电流 I的2 附近放一长为L,电流为 水平直导线，求载流直导线 所I受1 的力。
的I1
C
I 2 A I1 B aL
o x dx
解： B 0I2 2 x
（2）非均匀磁场中的直导线 d F Idl B
10第十讲 磁场对载流导线的作用、磁场对载流线圈的作用、磁力的功
结论：任意形状的平面线圈在均匀磁场中所受的合力 为零，但受到一力矩 M Pm B 作用。
11
1.当 Pm 与 B 的方向相互垂直( / 2 )，则 M M max Pm B NISB 2.当 M 0 ，但线圈处于非稳平衡，稍
受扰动就会加速偏转。 3.当 0 M 0 ，线圈处于稳定平衡状态。 F B F I I P Pm F m Pm F F I B B F
2
2.任意形状载流导线在均匀磁场中受力 设l为一段任意形状载流导线
F Idl B
l
a 0 a Ii B dx Ij B dy Ii B dx Iai B
0
lx
I (dxi dyj ) B l Idxi B Idyj B
ly
dl
B
I
l
o
L
a
L ai
F IL B
0
0
F ILB sin
结论：一段任意形状载流导线在均匀磁场中所受的安 培力与连接该线始末两端的直线电流受力相同。
3
3.直线电流在非均匀磁场中受力 例：计算电流I2L所受无限长直线电流I1的磁力。 I1 y 解法一： B1 dF I L 2 x 2 I1 dF I 2 dl B1 sin 90 l I 2 dl
dF
y
T
R
Fx
I
I
x
T
平衡时，有
2T Fx
T Fx / 2 IBR 0.35N
18
F应 T / S 0.5N/mm2
磁场对载流导线和载流线圈的作用
不在同一条直线上
M
F1
P O
I N
F4
F3 BIl1 sin (π ) F3 F4 在同一条直线上 F F1 F2 F3 F4 0
F2
B
en
O,P
F2
M F1l1 sin BIl2l1 sin M,N M BIS sin F1 M ISen B m B 线圈有N匝时 M NISen B
22
大学物理 （下）
例 3 求两平行无限长直导线之间的相互作用力？
解
电流 2 中单位长度上受的安培力
0 I1 电流 2 处于电流 1 的磁场中 B1 2a
0 I1 I 2 f12 I 2 B1 2a
I1
f 21 f12
I2
同时，电流 1 处于电流 2 的磁场中， 电流 1 中单位长度上受的安培力
第十章 稳恒电流的磁场
B
en
29
大学物理 （下）
e （1） n 与 B
稳定平衡
× × ×I × × × × × × × × × × ×
讨论
0 I1 I 2 f 21 I1 B2 2a
电流单位安培的定义:
B1
真空中通有同值电流的两无限长平行直导线，若相距 1 米，
a
单位长度受力2×10-7N，则电流为1 安培。
第十章 稳恒电流的磁场
23
大学物理 （下）
例4 求一载流导线框在无限长直导线磁场中的受力和运动 0 I1 1 f1 I 2bB1 I 2b I1 解 2a 2 方向向左 0 I1 3 f3 I 2bB3 I 2b I2 4a 方向向右 1 3 b 2a 2 f 2 I 2dlB1 sin a 2 2a I a 0 I1I 2 0 1 I 2dx ln 2 a a 2x 2 4 f4 f2 x 4 o
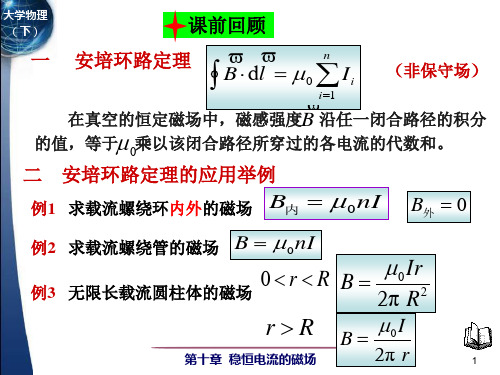
M
F1
P O
I N
F4
F3 BIl1 sin (π ) F3 F4 在同一条直线上 F F1 F2 F3 F4 0
F2
B
en
O,P
F2
M F1l1 sin BIl2l1 sin M,N M BIS sin F1 M ISen B m B 线圈有N匝时 M NISen B
22
大学物理 （下）
例 3 求两平行无限长直导线之间的相互作用力？
解
电流 2 中单位长度上受的安培力
0 I1 电流 2 处于电流 1 的磁场中 B1 2a
0 I1 I 2 f12 I 2 B1 2a
I1
f 21 f12
I2
同时，电流 1 处于电流 2 的磁场中， 电流 1 中单位长度上受的安培力
第十章 稳恒电流的磁场
B
en
29
大学物理 （下）
e （1） n 与 B
稳定平衡
× × ×I × × × × × × × × × × ×
讨论
0 I1 I 2 f 21 I1 B2 2a
电流单位安培的定义:
B1
真空中通有同值电流的两无限长平行直导线，若相距 1 米，
a
单位长度受力2×10-7N，则电流为1 安培。
第十章 稳恒电流的磁场
23
大学物理 （下）
例4 求一载流导线框在无限长直导线磁场中的受力和运动 0 I1 1 f1 I 2bB1 I 2b I1 解 2a 2 方向向左 0 I1 3 f3 I 2bB3 I 2b I2 4a 方向向右 1 3 b 2a 2 f 2 I 2dlB1 sin a 2 2a I a 0 I1I 2 0 1 I 2dx ln 2 a a 2x 2 4 f4 f2 x 4 o
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
II 22
B
I2 dlL
a
方向垂直纸面向里
安培力
df I 2dl B
I1
f
B
3
I2
由于各电流元受力方向相同
所以，合力方向指向I1 （如图）
合力大小：
f
df
I2
I dl B
2 I2
由于各电流元处 磁感强度相同
I 2 B dl
I2
m
fe F e
I
v
b
当qEH qB 时
电势差为
VH EH b Bb
12
E E d
4.霍尔系数 霍尔电阻
由电流强度的定义有
I nqdb
I nqdb
IB VH Bb nqd
n 单位体积中的粒子数
B
VH f fL
m
B
fe F e
I
v
b
E E d
霍尔系数
1 / nq
所以：洛仑兹力对施力点电荷不作功
9
二. 霍尔效应
1. 霍尔效应：在磁场中，载流导体或半导 体上出现横向电势差的现象
1879年美国物理 学家霍尔发现
2.霍尔电压：霍尔效应中产生的电势差
上图中导体上下两端面出现电势差
10
3.形成机制 以载流子为正电荷为例说明 设载流子速度为
•洛仑兹力使载流子横向漂移
dF
B
F Idl B
l
B
Id l
2
例1 如图所示 长直电流I1和长为L的电流I2平行 共面，相距为a。求I2受I1的磁场力。 解：在电流上任取一电流元
I 2dl 电流I1在电流元 I 2dl 处磁 0 I1 感强度为 B 2 πa
II11
df
14
3）粒子运动速度方向任意
1）粒子运动速度平行磁感强度
粒子不受力 粒子做匀速直线运动
q
0
B
2）粒子运动速度垂直磁感强度 B 0 f m q0 B fm q 粒子做匀速圆周运动 R
•圆周半径 由
q0 B m
02
R
得
m0 R qB
第14章 电流与磁力(自学)
§1 磁场对载流导线的作用力 安培力
§2 磁场对载流线圈的作用力矩
§3 磁场对运动电荷的作用力 洛仑兹力
1
§1 磁场对载流导线的作用力 安培力 一.安培定律 安培指出，任意电流元在磁场中受力为
dF Idl B
二.整个载流导线受力
dF
I
Id l
3）粒子运动速度方向任意
将上述两种情况综合
设粒子初速度与磁感强度之间夹角为
0 0 0
0 0 cos
0
q
0
B
0
R B
0 0 sin
0
粒子做螺旋运动
0
h
粒子在垂直磁场的平面里做圆周运动 同时又沿磁场方向匀速运动
I1
df
电流I1在x处磁感 强度为 I
B
o
a
I I 2dl 2 x B
L
x
0 1
2πx 安培力 df I 2dl B 方向如图
5
安培力大小为
df I 2dxB
0 I1 I 2dx
2πx
I1
df
o
a
因为各电流元受力方向相 同，所以大小直接相加
I I 2dl 2 x B
VH B RH B I nqd
霍尔电阻
13
三.带电粒子在磁场中运动
1.带电粒子在均匀磁场中运动
设均匀磁场磁感强度为 B
0
带电粒子质量为m 电量为q
fm
B
为了使物理图像清晰
我们分三种不同情况分别说明
1）粒子运动速度平行磁感强度
2）粒子运动速度垂直磁感强度
设粒子 初速度 为 0
出现电荷积累
洛仑兹力大小为 f qB
使载流子漂移 从而 上端积累了正电荷 下端积累了负电荷
VH f fL
m
B
v
E
B
b
Fe
I
d
11
•洛仑兹力与电场力平衡 载流子不再漂移 上下两端形成电势差 VH
由于电荷的积累，形成静电场－霍尔电场 EH B B 电荷受电力 Fe qEH
VH f fL
L
x
合力为：
a L
f
a
0 I1 I 2
2πx
dx
I1
f
a
L
I2
0 I1 I 2
aL ln 2π a
方向：垂直电流I2平行电流I1
6
§2 磁场对平面载流线圈的作用力矩
一.载流线圈在均匀磁场中的力矩
M Pm B
*二.载流线圈在均匀磁场中得到的能量 Wm Pm B 三.与静电场对比
II11
df
I2 2
B
L I2 dlL
a
f I 2 BL
0 I1 I 2 L
2 πa
#
I1
f
I2
代入数据得
f
B
4
例2 如图所示 长直电流I1和长为L的电流I2垂直 共面 相距为a 求I2受I1的磁场力 解：建坐标系如图 在坐标x处取电流元
ˆ I 2dl I 2dxx
M Pm B Wm Pm B
磁场
M Pe E We Pe E
静电场
7
§3 磁场对运动电荷的作用力 洛仑兹力 一 .洛仑兹力
磁场对运动电荷施以的磁场力是洛仑兹力
其表达式为： f q B m
式中： B q
15
m0 •圆周半径 R qB
由上式可知 圆周运动半径与 垂直磁场的速度有关 速度大的粒子圆周半径大 速度小的粒子圆柱半径小 •粒子运动的周期 T
2πR
B 0 fm q R
0
2πm 与速度无关 qB
由上式可知 同种粒子（m/q相同）不管其垂 直磁场方向的速度如何 在同样均匀磁场中圆 16 周运动的周期相同
17
•螺旋半径 •螺距
m0 m0 sin R qB qB
0
q
0
B
0
R B
应用 1）电真空器件中的磁聚焦
h T0 cos 2πm0 cos 0 qB
0
h
电子枪发射出一束电子 这束电子动能几乎相同
点电荷运动速度 点电荷处于场点处的磁感强度 点电荷电量
8
f m q B
如图所示点电荷受到磁场施以 的洛仑兹力大小为
q
f m qB sin
0 或π 时，f m 0
fm
B
由于： f m
π 3π 或 时，f m f max qB 2 2